Lowering dimension · Loginom Wiki. Introduction to a decrease in dimension What method helps to reduce the dimension of data
Chapter 13. Method of the main component
13.1. Essence of the problem of reduced dimension and various methods of its solution
In research and practical statistical work, it is necessary to deal with situations where the total number of signs recorded on each of the many subjects of the subjects (countries, cities, enterprises, families, patients, technical or environmental systems) is very large - about a hundred and more. Nevertheless, the existing multidimensional observations

it should be subjected to statistical processing, comprehend or enter into the database in order to be able to use them at the right time.
The desire of the statistics represent each of the observations (13.1) in the form of a vector z of some auxiliary indicators with a significantly smaller (than) number of components of the pillage is due primarily by the following reasons:
the need for a visual representation (visualization) of the source data (13.1), which is achieved by their projection on a specially selected three-dimensional space of the plane or numerical direct (objectives of this type IV);
the desire to laconism under investigated models due to the need to simplify the account and interpretation of the obtained statistical conclusions;
the need to substantially compress the volumes of stored statistical information (without visible losses in its informativeness), if it comes to the recording and storage of type arrays (13.1) in a special database.
At the same time, new (auxiliary) features can be selected from the number of initial or to be determined by any rule on the set of source signs, for example, their linear combinations. When forming new system Signs to the latter, I prevent our various kinds of requirements, such as the greatest informativeness (in a certain sense), mutual non-corrosionity, the smallest distortion of the geometric structure of a set of source data, etc., depending on the formal specification of these requirements (see below, and Also, section IV) We come to a particular dimension reduction algorithm. There are at least three basic types of fundamental prerequisites that determine the possibility of transition from a large number of source indicators of the state (behavior, functioning efficiency) of the analyzed system to a significantly smaller number of the most informative variables. This is, firstly, duplicating information delivered strongly interrelated signs; secondly, the non-informativeness of signs, little changing during the transition from one object to another (small "variability" of signs); Thirdly, the possibility of aggregation, i.e., a simple or "weighted" summation, according to some signs.
Formally the task of the transition (with the smallest loss in informative) to a new set of features can be described as follows. Suppose that - some p-dimensional vector function of the initial variables and let - in a certain way the specified measure of informativeness-dimensional system of features The specific choice of functional depends on the specifics of the solved real task and relies on one of the possible criteria: the Criterion of AutoFormativity, aimed at maximum saving information contained in the source array relative to the source signs; and the criterion of external informativeness aimed at the maximum "squeezing" of the information contained in this array relative to some other (external) indicators.
The task is to determine such a set of signs z, found in the class F of permissible transformations of the initial indicators that
One or another embodiment of this formulation (defining specific choice Informativeness measures) and class of permissible transformations) leads to a specific dimension reduction method: to the main component method, factor analysis, extreme grouping of parameters, etc.
Let us explain it on the examples.
13.1.1. Method of the main component (see § 13.2-§ 13.6).
It is to the first main components that the researcher will come, if the class of permissible transformations F will determine all sorts of linear orthogonal normalized combinations of initial indicators, i.e.

(here) - mathematical expectation A as a measure of informativeness -er-dimensional system indicators

(Here d, as before, the sign of the dispersion calculation operation of the corresponding random variable).
13.1.2. Factor analysis (see ch. 14).
As is known (see § 14.1), the model of factor analysis explains the structure of links between the initial indicators because the behavior of each of them statistically depends on the same set of so-called common factors.
where - the "load" of the general factor on the source indicator is the residual "specific" random component, and - in pairs are uncorrelated.
It turns out that if f, as a class of all kinds of linear combinations, taking into account the above-mentioned limits, to choose the value of the optimization problem (13.2) as a measure of informativeness (13.2), coincides with the common factors in the factor analysis model. Here - the correlation matrix of the initial indicators The correlation matrix of indicators - Euclidean norm of the matrix A.
13.1.3. Extreme grouping method (see section 14.2.1).
In this method, we are talking about such a partition of the set of initial indicators to a given number of groups that the signs belonging to the same group would be relatively strongly strongly, while the signs belonging to different groups would be correlated weakly. At the same time, the task of replacing each group of strongly intercreated initial indicators is solved by one auxiliary "asylum" indicator that, of course, should be in close correlation with the signs of its group. Having defined as a class of permissible transformations F of the initial indicators, all normalized linear combinations are looking for a solution maximizing (by s and) functionality

where is the correlation coefficient between variables.
13.1.4. Multidimensional scaling (see ch. 16).
In a number of situations, first of all, in situations where initial statistics are obtained using special surveys, questionnaires, expert estimates, there are cases where the element of the primary observation is not the state of the object described by the vector and the characteristic of pairwise proximity (remoteness) of two objects (or signs) respectively with numbers
In this case, the researcher has a matrix of size as an array of source statistical data (if the characteristics of the pairs of objects of objects are considered) or (if the characteristics of the pairs of signs of signs) of the species are considered
where the values \u200b\u200bare interpreted either as distances between objects (features) i and either as the ranks setting the streamlining of these distances. The task of multidimensional scaling is to "immerse" our objects (signs) in such a dimensional space, that is, to choose the coordinate axis so that the original geometric configuration of the set of analyzed points-objects (or points-features) specified by ( 13.1) or (13.5), it would be the least distorted in the sense of a certain criterion for the average "degree of distortion" of mutual pairs of distances.
One of the sufficient general schemes of multidimensional scaling is determined by the criterion.

where is the distance between objects in the source space, the distance between the same objects in the sought space of a smaller dimension - free parameters, the selection of specific values \u200b\u200bof which is made at the discretion of the researcher.
Identify a measure of the informativeness of the desired set of signs Z, for example, as a magnitude inversely mentioned above the value of the degree of distortion of the geometric structure of the original set of points, we reduce this task to the general formulation (13.2), believing
13.1.5. Selection of the most informative indicators in the models of the discriminant analysis (see § 1.4; 2.5).
The above functionals are the autographic informative meters of the corresponding system of signs. We now give examples of external informative criteria. In particular, we will be interested in the informativeness of the system of indicators from the point of view of the correctness of the classification of objects in these indicators in the discriminant analysis scheme. At the same time, the class of permissible transformations f we define on the requirements of the requirements that only representatives of the set of initial indicators can be considered, that is,.
A common source thesis in solving the problem of identifying the most informative indicators from the original set is the assertion that the vector of indicators of a given dimension is the more informative than the difference in the laws of its probabilistic distribution defined in different classes in the classification task under consideration. If you enter the mode of a pairwise difference in the laws describing the distribution of the probabilities of the characteristics of the characteristics in classes with numbers, it is possible to formalize the above principle of selection of the most informative indicators. Determining them from the maximization condition (software) of the magnitude

Most common measures differences between the laws of probability distribution are the distance information type (Distance Doljalkak, distance Mahalanobis), as well as "variation distance" (see more detail about it.
13.1.6. Selection of the most informative variables in regression models (see).
When constructing regression-type dependences, one of the central is to identify a relatively small number of variables (from a priori set of the most significant signs of the resulting result of the resulting result.
Thus, as in the previous paragraph, the class F consists of all sorts of sets of variables selected from the original set of argument factors and deal with the criterion of external informativeness of such sets. Its view is usually set using a multiple determination coefficient - the characteristics of the degree of tightness of the connection of the indicator y with a set of variables. At the same time, for a fixed dimension, the set of variables will be obviously considered the most informative (in terms of the accuracy of the description of the behavior of the indicator of the indicator), if the value of informativeness is on this The set reaches the maximum.
- In statistics, machine learning and information theory, the reduction of dimension is to convert data consisting in reducing the number of variables by receiving the main variables. Conversion can be divided into selection of features and selection of features.
Connected concepts
Mentioned in literature
- loading and preprocessing input data - manual and automatic layout of stimulus (selection of zones of interest), - algorithm for calculating the successor representation matrix, - building an extended data table with the values \u200b\u200bof the input variables required for subsequent analysis - method reduced dimension Space Spaces (Method of the main component), - visualization of component loads to select the interpretable component - the algorithm for learning the solutions tree, is an algorithm for assessing the predictive ability of the tree, - visualization of the solutions tree.
Related concepts (continued)
Spectral clustering techniques use spectrum (eigenvalues) of data similarity matrix to reduce dimension before clustering in smaller spaces. The similarity matrix is \u200b\u200bsupplied as an entry and consists of quantitative estimates of the relative similarity of each pair of points in the data.
Spectral methods are a class of technician used in applied mathematics for a numerical solution of some differential equations, it is possible to involve fast Fourier transform. The idea consists in census solving differential equations as the sum of some "basic functions" (for example, as Fourier series are the sum of the sinusoid), and then select the coefficients in the amount to satisfy the differential equation as much as possible.
Mathematical analysis (classical mathematical analysis) is a set of sections of mathematics corresponding to the historical section under the name "Analysis of infinitely small", combines differential and integral calculus.
Differential Evolution (eng. Differedial Evolution) - Method of multidimensional mathematical optimization related to the class of stochastic optimization algorithms (that is, it works using random numbers) and using some ideas of genetic algorithms, but, unlike them, does not require work with variables in binary code.
The method of the discrete element (DEM, from the English. Discrete Element Method) is a family of numerical methods intended for calculating the movement of a large number of particles, such as molecules, gravel, gravel, pebbles and other granulated media. The method was originally applied CUNDALL in 1971 to solve problems of rock mechanics.
Purpose of the study:
Evaluation of the effectiveness of the data dimension reduction methodology to optimize their application in recognition practice (identification).
Research tasks:
1. Review of literary sources about existing methods Reduce data dimension.
2. Conducting research (experiments) to compare the effectiveness of the data reduction algorithms applied in practice in the classification tasks
Research methods (software):
C ++ Programming Language, OpenCV Library
The perception of high dimension data for a person is difficult, and sometimes it is impossible. In this regard, quite natural was the desire to move from a multidimensional sample to the data of a small dimension so that "they could look at them," evaluate and use, including to achieve recognition tasks. In addition to visibility, the reduction in dimension allows you to get rid of factors (information) that interfere with statistical analysis, extending the time for collecting information, increasing the dispersion of estimates of parameters and characteristics of distributions.
Reduction of dimension is the transformation of source data with a large dimension in a new representation of a smaller dimension that maintains basic information. In the perfect case, the dimension of the converted representation corresponds to the internal dimension of the data. Internal data dimension is the minimum number of variables required to express all possible data properties. An analytical model, built on the basis of a reduced multiple data, should be easier for processing, implementation and understanding than the model built on the source set.
The decision on the choice of the reduction method of dimension is based on knowledge of the features of the task being solved and the expected results, as well as limited time and computational resources. According to literary reviews, the most commonly used dimension reduction methods include PrincIpal Component Analisys (PCA), Independent Component Analisys (ICA) and Singular Value Decomposition (SVD).
Analysis of the main component (PCA) - The easiest method of reducing the dimension of the data. It is widely used to convert signs while reducing the dimension of data in classification tasks. The method is based on projection of data to a new coordinate system of a smaller dimension, which is determined by its own vectors and the own numbers of the matrix. From the point of view of mathematics, the main component method is an orthogonal linear transformation.
The main idea of \u200b\u200bthe method is to calculate the eigenvalues \u200b\u200band the eigenvectors of the covariance matrix of data in order to minimize the dispersion. The covariance matrix is \u200b\u200bused to determine the scatter relative to the average relative to each other. Covariance of two random variables (dimensions) - measure of their linear dependence:
where - the mathematical expectation of the random value of X, - the mathematical expectation of the random variable y. We can also write down the formula (1) in the form:

where - the mean x, where - the average Y, n is the dimensionality of the data.
After calculating its own vectors and their own numbers, their values \u200b\u200bare sorted in descending order. Thus, the components are obtained in order to reduce significance. Own vector with the largest natural number and is the main component of the data set. The main components are obtained by multiplying rows from its own vectors on sorted eigenvalues. To find the optimal space of a smaller dimension, formula (3) is used, which calculates the minimum error between the source set of data and the following criterion:

where P is the dimension of the new space, n is the dimension of the original sample, - eigenvalues, - threshold. During the operation of the algorithm, we obtain a matrix with MP data, linearly converted from Mn, after which the PCA finds a linear mapping M, a minimizing estimate function:

where - Euclidean distance between points and, - Euclidean distance between points and ,, ![]() . The minimum of this estimated function can be calculated by performing a spectral decomposition of the gram matrix and multiplying its own vector of this matrix to the root from the corresponding eigenvalues.
. The minimum of this estimated function can be calculated by performing a spectral decomposition of the gram matrix and multiplying its own vector of this matrix to the root from the corresponding eigenvalues.
Analysis of independent components ( ICA ) , Unlike PCA, a new enough, but quickly gaining popularity method. It is based on the idea of \u200b\u200ba linear data transformation into new components, which are most statistically independent and optionally orthogonal to each other. For research in this paper, the Fastica algorithm was selected, described in detail in the article. The main tasks this method These are centered (subtracting average of data) and "bleaching" (linear conversion of vector x in vector with uncorrelated coordinates, the dispersion of which is equal to one).
Independence Criterion in Fastica is non-geasura, which is measured using the Excesses coefficient:
For Gaussian random variables, this value is zero, so Fastica maximizes its value. If - "bleached" data, then the matrix of covariance of "bleached" data is a single matrix.
![]()
Such transformation is always possible. The popular method of "bleaching" uses the spectral decomposition of the covariance matrix ![]() , where - the orthogonal matrix of its own vectors, A is a diagonal matrix of own numbers,. It turns out that "whitening" can be represented as:
, where - the orthogonal matrix of its own vectors, A is a diagonal matrix of own numbers,. It turns out that "whitening" can be represented as:
where the matrix is \u200b\u200bcalculated by the pomoponent operation:
Experiments
For the experimental study of the proposed methods, a dictionary-based video sequence from the Casia Gait database was used. The base contains the sequences of binary images corresponding to individual frames of the video sequence on which the allocation of moving objects has already been made.
Of all the many videos, 15 classes were randomly taken, in which the shooting angle is 90 degrees, people are depicted in ordinary non-winter clothes and without bags. In each class there were 6 sequences. The length of each sequence was at least 60 frames. Classes were divided into learning and test samples of 3 sequences each.
The features obtained as a result of PCA and ICA methods were used to study the classifier, which in the present work was the support vectors (Support Vector Machines, SVM).
To determine the quality of the method of the method, the accuracy of the classification was estimated, defined as the proportion of correctly classified objects. During the experiment, the time spent in the mode of training and testing was also fixed.


Figure 1. (a) Method Main Component (PCA) b) independent component method (ICA)
Figure 1 (A, B) presents the relationship of the classification accuracy from the value of the output dimension of the data after the conversion. It can be seen that in PCA the accuracy of the classification with an increase in the number of components varies slightly, and when using ICA, accuracy starting from a certain value, starts to fall.


Figure 2. The dependence of the classification time on the number of components but) PCA b) ICA
Figure 2 (A, B) presents the dependence of the classification time on the number of PCA components and ICA. The growth of dimension in both cases was accompanied by a linear increase in processing time. The graphs show that the SVM classifier worked faster after lowering the dimension using the Main Component Method (PCA).
PRINCIPAL COMPONENT ANALISYSYS (PCA), Independent Component Analisys (ICA) worked fast enough and defined parameters High results were obtained in the classification task. But with data with a complex structure, these methods do not always allow you to achieve the desired result. Therefore B. lately Local nonlinear methods are increasingly paid to the projection of data on some variety, which allows you to maintain the data structure.
In the future, it is planned to expand both the list of algorithms used to form a feature description and a list of classification methods used. Another important area of \u200b\u200bresearch seems to reduce processing time.
Bibliography:
- Jolliffe, I.T, Principal Component Analysis, Springer, 2002
- Hyvärinen and Erkki Oja, Independent Component Analysis: Algorithms and Applications, Neural Networks, 13, 2000
- Josiński, H. FEATURE EXTRACTION AND HMM-BASED CLASSIFICATION OF GAIT Video Sequences for the Purpose of Human Identification / Springer, 2013 - VOL 481.
Keywords
MATHEMATICS / Applied statistics / MATH STATISTICS / Growth points / Method of the main component / FACTOR ANALYSIS / Multidimensional scale / Evaluation of data dimension / Estimation of the dimension of the model / Mathematics / Applied Statistics / Mathematic Statistics / Growth Points / Principal Component Analysis / Factor Analysis / Multidimensional Scaling / Estimation of Data Dimension / Estimation of Model Dimensionannotation scientific article in mathematics, author of scientific work - Orlov Alexander Ivanovich, Lutsenko Evgeny Veniaminovich
One of the "Growth Points" applied statistics are methods to reduce the dimension of the space of statistical data. They are increasingly used in analyzing data in specific applied studies, for example, sociological. Consider the most promising methods of reduced dimension. Method of the main component It is one of the most commonly used dimension methods. For visual analysis of data, projections of the initial vectors on the plane of the first two main components are often used. Usually, the data structure is clearly visible, compact object clusters and separately released vector are distinguished. Method of the main component is one of the methods factor analysis. New idea compared to method of main components It is that on the basis of loads, the factors are divided into groups. In one group, factors are combined, having a similar effect on the elements of the new base. Then from each group it is recommended to leave one representative. Sometimes, instead of choosing a representative, a new factor is formed, which is central for the group under consideration. The reduction in dimension occurs during the transition to the system of factors that are representatives of groups. The remaining factors are discarded. On the use of distances (proximity measures, differences indicators) between the signs and the extensive class of methods is based multidimensional scaling. The main idea of \u200b\u200bthis method of methods is to represent each object of the point of geometric space (usually dimension 1, 2 or 3), the coordinates of which serve as the values \u200b\u200bof hidden (latent) factors, which are quite adequately describing the object. As an example of the application of probabilistic statistical modeling and results of non-statinists, we justify the consistency of the measurement of the dimension of the data space in multidimensional scalingpreviously proposed by colromal from heuristic considerations. Considered a number of works on assessment of the dimensions of the models (in regression analysis and in the theory of classification). Dana Information about the algorithms reduction of dimension in an automated system-cognitive analysis
Similar topics scientific work on mathematics, author of scientific work - Orlov Alexander Ivanovich, Lutsenko Evgeny Veniaminovich
-
Mathematical methods in sociology for forty five years
-
Variety of objects of non-Nature
-
Evaluation of parameters: One-step estimates are preferable to maximum credibility estimates
-
Applied Statistics - Statistics and Perspectives
2016 / Orlov Alexander Ivanovich -
State and prospects for the development of applied and theoretical statistics
2016 / Orlov Alexander Ivanovich -
The relationship of the limit theorems and the Monte Carlo method
2015 / Orlov Alexander Ivanovich -
On the development of statistics of non-Nature objects
2013 / Orlov Alexander Ivanovich -
Points of growth of statistical methods
2014 / Orlov Alexander Ivanovich -
About new promising mathematical instruments of controlling
2015 / Orlov Alexander Ivanovich -
Distances in statistical spaces
2014 / Orlov Alexander Ivanovich
ONE OF THE "POINTS OF GROWTH" OF APPLIED STATISTICS IS METHODS OF REDUCING THE DIMENSION OF STATISTICAL DATA. They Are Increasingly Used in the Analysis of Data in Specific Applied Research, Such As Sociology. We Investigate The Most Promising Methods to Reduce The Dimensionality. The Principal Components Are One of the Most Commonly Used Methods to Reduce The Dimensionality. For Visual Analysis of Data Are Often Used The Projections of Original Vectors on the Plane of the First Two Principal Components. USUALY THE DATA STRUCTURE IS CLEARLY VISIBLE, HIGHLIGHTED COMPACT CLUSTSERS OF OBJECTS AND SEPARETELY ALLOCATED VECTORS. The Principal Components Are One Method of Factor Analysis. The New Idea of \u200b\u200bFactor Analysis In Comparison With the Method of Principal Components Is That, Based on Loads, The Factors Breaks Up Into Groups. In One Group of Factors, New Factor IS Combined with a Similar Impact on the Elements of the New Basis. Then Each Group IS Recommended to Leave One Representative. Sometimes, Instead of the Choice of Representative by Calculation, A New Factor That Is Central To The Group in Question. Reduced Dimension Occurs During The Transition to the System Factors, Which Are Representatives of Groups. Oter Factors Are Discarded. ON USE OF DISTANCE (Proximity Measures, Indicators of Differences) Between Features and Extensive Class Are Based Methods of Multidimensional Scaling. The Basic Idea of \u200b\u200bthis Class of Methods Is To Present Each Object As Point of the Geometric Space (Usually of Dimension 1, 2, OR 3) Whose Coordinates Are The Values \u200b\u200bof the Hidden (Latent) Factors Which Combine to Adequately Describe The Object. As an example of the application of probabilistic and statistical modeling and the results of statistics of non-numeric data, we justify the consistency of estimators of the dimension of the data in multidimensional scaling, which are proposed previously by Kruskal from heuristic considerations. We Have Considered A Number of Consistent Estimations of Dimension of Models (in Regression Analysis and In Theory of Classification). WE ALSO GIVE SOMEFORMATION ABOUT THE ALGORITHMS FOR REDUCE THE DIMENSIONALITY IN THE AUTOMATED SYSTEM-COGNITIVE ANALYSIS
Text of scientific work on the topic "Methods to reduce the dimension of the space of statistical data"
UDC 519.2: 005.521: 633.1: 004.8
01.00.00 Physics and mathematics
Methods to reduce the dimension of the statistical data space
Orlov Alexander Ivanovich
d.E.N., D.T.N., K.F.-M.N., Professor
Rinz Brosh code: 4342-4994
Moscow State Technical
university. AD Bauman, Russia, 105005,
Moscow, 2nd Baumanskaya st., 5, [Email Protected]t.
Lutsenko Evgeny Veniaminovich D.E.N., Ph.D., Professor Rinz Brosh code: 9523-7101 Kuban State Agrarian University, Krasnodar, Russia [Email Protected] Com.
One of the "Growth Points" of application statistics is methods to reduce the dimension of the statistical data space. They are increasingly used in analyzing data in specific applied studies, for example, sociological. Consider the most promising methods of reduced dimension. The main component method is one of the most commonly used dimension reduction methods. For visual analysis of data, projections of the initial vectors on the plane of the first two main components are often used. Usually, the data structure is clearly visible, compact object clusters and separately released vector are distinguished. The main component method is one of the methods of factor analysis. The new idea compared to the main component method is that on the basis of loads, factors are divided into groups. In one group, factors are combined, having a similar effect on the elements of the new base. Then from each group it is recommended to leave one representative. Sometimes, instead of choosing a representative, a new factor is formed, which is central for the group under consideration. The reduction in dimension occurs during the transition to the system of factors that are representatives of groups. The remaining factors are discarded. On the use of distances (proximity measures, differences indicators) between the signs and the extensive class of multidimensional scaling methods is founded. The main idea of \u200b\u200bthis class of methods is to represent each object with a point of geometric space (usually dimension 1, 2 or 3), the coordinates of which are the values \u200b\u200bof hidden (latent) factors, in the aggregate, sufficiently adequately describing
UDC 519.2: 005.521: 633.1: 004.8
PHYSICS AND MATHEMATICAL SCIENCES
Methods of Reducing Space Dimension Of Statistical Data
Orlov alexander ivanovich
Dr.SCI.CHON., DR.SCI.TECH., CAND.PHYS-MATH.SCI.,
Bauman Moscow State Technical University, Moscow, Russia
Lutsenko Eugeny Veniaminovich Dr.SCI.CON., CAND.TECH.SCI., Professor RSCI Spin-Code: 9523-7101
Kuban State Agrarian University, Krasnodar, Russia
prof.Lutse [Email Protected] Com.
ONE OF THE "POINTS OF GROWTH" OF APPLIED STATISTICS IS METHODS OF REDUCING THE DIMENSION OF STATISTICAL DATA. They Are Increasingly Used in the Analysis of Data in Specific Applied Research, Such As Sociology. We Investigate The Most Promising Methods to Reduce The Dimensionality. The Principal Components Are One of the Most Commonly Used Methods to Reduce The Dimensionality. For Visual Analysis of Data Are Often Used The Projections of Original Vectors on the Plane of the First Two Principal Components. USUALY THE DATA STRUCTURE IS CLEARLY VISIBLE, HIGHLIGHTED COMPACT CLUSTSERS OF OBJECTS AND SEPARETELY ALLOCATED VECTORS. The Principal Components Are One Method of Factor Analysis. The New Idea of \u200b\u200bFactor Analysis In Comparison With the Method of Principal Components Is That, Based on Loads, The Factors Breaks Up Into Groups. In One Group of Factors, New Factor IS Combined with a Similar Impact on the Elements of the New Basis. Then Each Group IS Recommended to Leave One Representative. Sometimes, Instead of the Choice of Representative by Calculation, A New Factor That Is Central To The Group in Question. Reduced Dimension Occurs During The Transition to the System Factors, Which Are Representatives of Groups. Oter Factors Are Discarded. ON USE OF DISTANCE (Proximity Measures, Indicators of Differences) Between Features and Extensive Class Are Based Methods of Multidimensional Scaling. The Basic Idea of \u200b\u200bthis Class of Methods Is To Present Each Object As Point of the Geometric Space (Usually of Dimension 1, 2, OR 3) Whose Coordinates Are The Values \u200b\u200bof the Hidden (Latent) Factors Which Combine to Adequately Describe The Object. AS An Example Of The Application Of ProBabilistic and Statistical Modeling And The Results of Statistics of Non-Numeric Data, We Justify The Consistency of Estimators Of The
an object. As an example of the application of probabilistic statistical modeling and results of non-non-statistics statistics, we substantiate the consistency of the measurement of the dimension of the data space in multidimensional scaling, previously proposed by colromal from heuristic considerations. A number of work on the assessment of the dimensions of the models (in regression analysis and in the theory of classification) were considered. Dana Information about the algorithms reduction of dimension in an automated system-cognitive analysis
Keywords: mathematics, applied statistics, mathematical statistics, growth points, main component method, factor analysis, multidimensional scaling, data dimension estimation, model dimension estimation
dimension of the Data in Multidimensional Scaling, Which Are Proposed Previously by Kruskal from Heuristic Considerations. We Have Considered A Number of Consistent Estimations of Dimension of Models (in Regression Analysis and In Theory of Classification). WE ALSO GIVE SOMEFORMATION ABOUT THE ALGORITHMS FOR REDUCE THE DIMENSIONALITY IN THE AUTOMATED SYSTEM-COGNITIVE ANALYSIS
Keywords: Mathematics, Applied Statistics, Mathematical Statistics, Growth Points, The Principal Component Analysis, Factor Analysis, Multidimensional Scaling, Estimation of Data Dimension, Estimation of Model Dimension
1. Introduction
As already noted, one of the "growth points" of application statistics are methods of reducing the dimension of the statistical data space. They are increasingly used in analyzing data in specific applied studies, for example, sociological. Consider the most promising methods of reduced dimension. As an example of the application of probabilistic statistical modeling and the results of non-statistics, we justify the consistency of the size of the size of the space previously proposed by colromic from heuristic considerations.
In multidimensional statistical analysis, each object is described by a vector, the dimension of which is arbitrary (but the same for all objects). However, a person can directly perceive only numeric data or points on the plane. Analyze the accumulations of points in the three-dimensional space is already much more difficult. Direct perception of data of higher dimension is impossible. Therefore, quite natural is the desire to move from a multidimensional sample to data of a small dimension so that "they could
look". For example, a marketer can clearly see how many different types of consumer behavior (i.e., how much it is advisable to allocate market segments) and which properties are (with what properties) consumers in them.
In addition to the desire for clarity, there are other motifs to reduce dimension. Those factors from which the variable is interested in the researcher do not only interfere with statistical analysis. First, financial, temporary, personnel resources are spent on collecting information about them. Secondly, how to prove, their inclusion in the analysis worsens the properties of statistical procedures (in particular, increases the dispersion of estimates of parameters and characteristics of distributions). Therefore, it is desirable to get rid of such factors.
When analyzing multidimensional data, not one, but many tasks, in particular, choosing independent and dependent variables in different ways. Therefore, we consider the problem of reduced dimension in the following wording. Dana multidimensional sample. It is required to move from it to the totality of vectors of a smaller dimension, while saving the structure of the source data, if possible, without losing information contained in the data. The task is specified within each particular method of reduced dimension.
2. Method of the main component
It is one of the most commonly used dimension methods. The main idea is consistent with the detection of areas in which the data has the greatest scatter. Let the sample consist of vectors equally distributed with the vector x \u003d (x (1), x (2), ..., x (n)). Consider linear combinations
7 (^ (1), x (2) ,., L (n)) \u003d x (1) x (1) + x (2) x (2) + ... + L (n) x (n) .
X2 (1) + x2 (2) + ... + x2 (n) \u003d 1. Here, vector x \u003d (x (1), x (2), ..., x (n)) lies on the unit sphere in p-dimensional space.
In the main component method, first of all find the direction of maximum scatter, i.e. Such X, at which the maximum dispersion of a random variable is 7 (x) \u003d 7 (x (1), x (2), ..., x (n)). Then the vector X sets the first main component, and the value of 7 (x) is the projection of the random vector x on the axis of the first main component.
Then, expressing the terms of linear algebra, consider the hyperplane in the p-dimensional space, perpendicular to the first main component, and design all the elements of the sample on this hyperplane. The dimension of the hyperplane is 1 less than the dimension of the source space.
In the hyperplane under consideration, the procedure is repeated. It finds the direction of the greatest scatter, i.e. Second main component. Then the hyperplane perpendicular to the first two main components is isolated. Its dimension is 2 less than the dimension of the source space. Next - the next iteration.
From the point of view of the linear algebra we are talking about building a new basis in a p-dimensional space, whose iths serve as the main components.
Dispersion corresponding to each new main component, less than for the previous one. Usually stop when it is less than the specified threshold. If it is selected to the main components, this means that from the p-dimensional space it was possible to go to K-dimensional, i.e. Reduce the dimension with P-TO K, practically without distorting the structure of the source data.
For visual analysis of data, projections of the initial vectors on the plane of the first two main components are often used. Usually
the data structure is clearly visible, compact object clusters and separately released vector are distinguished.
3. Factor analysis
The main component method is one of the methods of factor analysis. Various algorithms for factor analysis are combined by the fact that in all of them there is a transition to a new basis in the initial N-dimensional space. Important is the concept of "factor load" used to describe the role of the source factor (variable) in the formation of a certain vector from the new base.
The new idea compared to the main component method is that on the basis of loads, factors are divided into groups. In one group, factors are combined, having a similar effect on the elements of the new base. Then from each group it is recommended to leave one representative. Sometimes, instead of choosing a representative, a new factor is formed, which is central for the group under consideration. The reduction in dimension occurs during the transition to the system of factors that are representatives of groups. The remaining factors are discarded.
The described procedure can be carried out not only with the help of factor analysis. We are talking On a cluster-analysis of signs (factors, variables). To split signs of groups, various cluster analysis algorithms can be applied. It is enough to enter the distance (measure of proximity, the difference indicator) between the signs. Let x and y be two signs. The difference D (x, y) between them can be measured using selective correlation coefficients:
di (x, y) \u003d 1 - \\ rn (x, y) \\, d2 (x, y) \u003d 1 - \\ pn (x, y) \\, where Rn (x, y) is a selective linear Pearson correlation coefficient, Pn (x, y) is a selective coefficient of the river correlation of the spirme.
4. Multidimensional scaling.
On the use of distances (proximity measures, differences indicators) D (x, y) between the signs X and U, the extensive class of multidimensional scaling methods is based. The main idea of \u200b\u200bthis method of methods is to represent each object of the point of geometric space (usually dimension 1, 2 or 3), the coordinates of which serve as the values \u200b\u200bof hidden (latent) factors, which are quite adequately describing the object. At the same time, relations between objects are replaced by relations between points - their representatives. So, data on the similarity of objects - distances between points, the data on superiority - the mutual location of the points.
5. The problem of assessing the true dimension of the factor space
In the practice of analyzing sociological data used different models Multidimensional scaling. In all of them, the problem of assessing the true dimension of the factor space. Consider this problem on the example of processing data on the similarity of objects using metric scaling.
Let there be n objects 0 (1), o (2), ..., o (n), for each pair of objects 0 (/), o (j), the measure of their similarity S (IJ) is given. We believe that always S (i, j) \u003d s (j, i). The origin of the number S (ij) does not matter to describe the operation of the algorithm. They could be obtained either by direct measurement, or using experts, or by calculating the combination of descriptive characteristics, or somehow otherwise.
In the Euclidean space, the N objects under consideration should be represented by the configuration of n points, and the Euclidean distance D (I, J) appears as the measure of proximity of the points-representatives
between the corresponding points. The degree of conformity between the set of objects and the combination of their points is determined by comparing the similarity matrices || I (,) || and distances of the SM-metric functionality of similarities
i \u003d £ | * (/,]) - th (/, m
The geometric configuration must be selected so that the functional S reached its smallest value.
Comment. In nonethenetic scaling, instead of the proximity of the proximity and distances themselves, the proximity of orderlios on the set of proximity measures and the set of corresponding distances is considered. Instead of the S functional, the analogues of the rank coefficients of the correlation of the spirit and Kendalla are used. In other words, non-metric scaling comes from the assumption that the proximity measures are measured in the ordinal scale.
Let the Euclidean space be dimension t. Consider at least the mid-square error
where the minimum is taken in all possible configurations of points in T-Merne Euclidean space. It can be shown that the minimum in question is achieved on some configuration. It is clear that with the growth of t, the value of AT monotonically decreases (more precisely, it does not increase). It can be shown that at T\u003e P - 1 it is equal to 0 (if - metric). To increase the possibilities of meaningful interpretation, it is desirable to act in space possible less dimension. At the same time, however, the dimension must be chosen so that the points represent objects without great distortion. The question arises: how to rationally choose the dimension of the space, i.e. Natural number t?
6. Models and methods for estimating the dimension of the data space
As part of the deterministic analysis of the data of a reasonable answer to this question, apparently not. Therefore, it is necessary to study the behavior of AM in certain probabilistic models. If the proximity of S (IJ) is random values, the distribution of which depends on the "true dimension" m0 (and possibly from any other parameters), then in the classical mathematic-statistical style, to set the M0 estimate task, to look for wealthy assessments and etc.
Let's start building probabilistic models. We will assume that objects are points in the Euclidean space of dimension to, where large enough. The fact that the "true dimension" is equal to M0, means that all these points lie on the hyperplane of the dimension M0. We accept for certainty that the set of the points under consideration is a sample of circular normal distribution with dispersion O (0). This means that objects 0 (1), 0 (2), ..., O (n) are independent in the aggregate of random vectors, each of which is built as
Z (1) e (1) + z (2) e (2) + ... + z (m0) e (m0), where E (1), E (2), ..., E (M0) - Ortonormal basis in the subspace of the dimension M0, in which the considered points under consideration, and z (1), z (2), z (m0) are independent in the aggregate one-dimensional normal random variables with mathematical expectation 0 and dispersion O (0).
Consider two models for obtaining proximity s (IJ). In the first of these, S (IJ) differ from the Euclidean distance between the corresponding points due to the fact that points are known to distortion. Let with (1), with (2), ..., c (n) - the points under consideration. Then
s (i, j) \u003d d (C (I) + E (I), C (J) + S (/)), ij \u003d 1, 2, ..., n,
where y is the Euclidean distance between points in the measurement space, the vector E (1), E (2), ..., E (P) are a sample of a circular normal distribution of a measuring space with a zero mathematical expectation and a covariance matrix on (1) /, where i-a -edite matrix. In other words,
e (0 \u003d p (1) e (1) + p (2) e (2) + ... + c (k) in (k), where e (1), e (2), ... e (k) - orthonormal basis in a measuring space, and [C ^^), I \u003d 1, 2, ..., p ,? \u003d 1, 2, ..., K) is a set of independent in the aggregate of one-dimensional random variables with zero mathematical expectation and dispersion of O (1).
In the second model of distortion are imposed directly to the distances themselves:
Kch) \u003d th (f \\ s)) + £ (uh and \u003d 1, 2., N, i f j,
where and, and on the first interval, it decreases faster than on the second. From here it follows that statistics
m * \u003d Arg MINAM + 1 - 2AM + AN-X)
it is a wealthy assessment of the true dimension M0.
So, of the probabilistic theory implies the recommendation - as an estimate of the dimension of the factorial space to use T *. Note that such a recommendation was formulated as an heuristic one of the founders of multidimensional scaling by J. Kraskal. He proceeded from the experience of the practical use of multidimensional scaling and computational experiments. Probabilistic theory made it possible to justify this heuristic recommendation.
7. Evaluation of the dimension of the model
If possible subsets of signs form an expanding family, for example, the degree of polynomial is estimated, it is natural to introduce the term "model dimension" (this concept is largely similar to the dimension of the data space in multidimensional scale). The author of this article has a number of work on the evaluation of the dimension of the model, which it is advisable to compare with the work on the estimation of the dimension of the data space, discussed above.
The first such work was performed by the author of this article during a trip to France in 1976. One assessment of the dimension of the model in regression was studied in it, namely, an assessment of the degree of polynomial under the assumption that the dependence is described by the polynomial. This estimate was known in the literature, but later it became mistaken to attribute to the author of this article, which only studied its properties, in particular, found that it is not wealthy, and found its limit geometric distribution. Others, already wealthy estimates of the dimension of the regression model were proposed and studied in the article. This cycle completed the work containing a number of refinements.
The extreme publication on this subject includes a discussion of the results of studying the speed of convergence in the limit theorems obtained by Monte Carlo.
Similar to the methodology for estimating the dimension of the model in the problem of splitting mixtures (part of the classification theory) are considered in the article.
The above estimates of the dimension of the model in multidimensional scaling are studied in the works. In the same works, the limit behavior of the characteristics of the method of the main components (using the asymptotic theory of the behavior of the decisions of extreme statistical problems).
8. Dimension reduction algorithms in an automated system-cognitive analysis
The automated system-cognitive analysis (ASC-Analysis) is also proposed in the EIDOS system, another method of reduced dimension is implemented. It is described in work in sections 4.2 "Description of algorithms of basic cognitive operations of system analysis (BKOS)" and 4.3 "Detailed BKOS algorithms (ASK analysis)". Here short description Two algorithms - BKOS-4.1 and BKOS-4.2.
BKOSA-4.1. "The abstraction of factors (reducing the dimension of the semantic space of factors)"
Using the method of consecutive approximations (iterative algorithm), at a given boundary conditions, the dimension of the attribute space is reduced without a significant decrease in its volume. The criterion for stopping the iterative process is to achieve one of the boundary conditions.
BKOS-4.2. "Abstraction of classes (decrease in the dimension of the semantic space of classes)"
Using the method of consecutive approximations (iterative algorithm), under specified boundary conditions, the size of the space of classes is reduced without a significant reduction in its volume. The criterion for stopping the iterative process is to achieve one of the boundary conditions.
Here are all the real algorithms implemented in the Eidos system of the version that was implemented at the time of work preparation (2002): http: //lc.kubagro .ru / aidos / aidos02 / 4.3 .htm
The essence of algorithms is as follows.
1. The amount of information is calculated in the values \u200b\u200bof the object transition to the status corresponding to classes.
2. Calculates the value of the factor value for differentiation of the object by classes. This value is simply the variability of the informatives of the values \u200b\u200bof factors (quantitative measures of variability a lot: the average deviation from the average, the average quadratic deviation, etc.). In other words, if in the value of the factor on average, there is little information about belonging and not belonging to the object to class, then this value is not very valuable, and if much is valuable.
3. Calculates the value of descriptive scales for differentiation of objects by classes. In the works of E.V. Lutsenko is now done as average from the values \u200b\u200bof gradations of this scale.
4. Then the pass-optimization of the values \u200b\u200bof factors and descriptive scales is carried out:
The values \u200b\u200bof the factors (gradations of the descriptive scaling) are ranked in the order of decreasing value and are removed from the model the least valuable, which go to the right of the Pareto-curve of 45 °;
Factors (descriptive scales) are ranked in descending order of value and are removed from the model of the least valuable, which go to the right of 45 ° the pass-curve.
As a result, the dimension of the space built on the descriptive scales is significantly reduced by removing the scales correlating among themselves, i.e. In essence, it is orthonormaling space in an information metric.
This process may be repeated, i.e. be iterative at the same time new version The "EIDOS" system is manually started.
Similarly, the information space of classes is omitted.
Scale and gradations can be numeric (then interval values \u200b\u200bare processed), and may also be text (ordinal or even nominal).
Thus, with the help of BKOS algorithms (ASK analysis), the dimension of space is maximally reduced with the minimum loss of information.
To analyze statistical data in applied statistics, a number of other dimension reduction algorithms have been developed. The tasks of this article does not include a description of the whole manifold of such algorithms.
Literature
1. Orlov A.I. Points of growth of statistical methods // Polygraph Network Electronic Scientific Journal of the Kuban State Agrarian University. 2014. No. 103. P. 136-162.
2. Paint J. Relationship between multidimensional scaling and cluster analysis // Classification and cluster. M.: Mir, 1980. C.20-41.
4. Harman G. Modern factor analysis. M.: Statistics, 1972. 489 p.
5. Orlov A.I. Notes on classification theory. / Sociology: methodology, methods, mathematical models. 1991. No. 2. C.28-50.
6. Orlov A.I. Basic results of the mathematical theory of classification // Polymatic Network Electronic Scientific Journal of the Kuban State Agrarian University. 2015. № 110. P. 219-239.
7. Orlov A.I. Mathematical methods Classification theories // Polygraph Network Electronic Scientific Journal of the Kuban State Agrarian University. 2014. No. 95. P. 23 - 45.
8. Terekhina A.Yu. Analysis of these methods of multidimensional scaling. -M.: Science, 1986. 168 p.
9. Perekrest V. T. Nonlinear typological analysis of socio-economic information: mathematical and computational methods. - L.: Science, 1983. 176 p.
10. Tyurin Yu.N., Litvak B.G., Orlov A.I., Satarov G.A., Smerling D.S. Analysis of non-invalid information. M.: Scientific Council of the Academy of Sciences of the USSR on the complex problem "Cybernetics", 1981. - 80 s.
11. Orlov A.I. A general view of the statistics of non-Nature objects // Analysis of non-information information in sociological studies. - M.: Science, 1985. S.58-92.
12. Orlov A.I. The limit distribution of one estimate of the number of basic functions in regression // Applied multidimensional statistical analysis. Scientists on statistics, T.33. - M.: Science, 1978. p.380-381.
13. Orlov A.I. Assessment of the dimension of the model in regression // Algorithmic and software Applied statistical analysis. Scientists for statistics, T.36. - M.: Science, 1980. P.92-99.
14. Orlov A.I. Asymptotics of some estimates of the dimension of the model in regression // Applied statistics. Scientists for statistics, T.35. - M.: Science, 1983. P.260-265.
15. Orlov A.I. On the assessment of the regression polynomial // Factory Laboratory. Diagnosis of materials. 1994. T.60. № 5. P.43-47.
16. Orlov A.I. Some probabilistic classification theory questions // Applied statistics. Scientists for statistics, T.35. - M.: Science, 1983. C.166-179.
17. Orlov A.I. On the Development of the Statistics of Nonnumerical Objects // Design of Experiments and Data Analysis: New Trends and Results. - M.: Antal, 1993. R.52-90.
18. Orlov A.I. Methods of reduction of dimension // Appendix 1 to the book: Tolstova Yu.N. Basics of multidimensional scaling: Tutorial For universities. - M.: Publisher CDU, 2006. - 160 p.
19. Orlov A.I. Asymptotics of extremal statistical problems // Analysis of non-numeric data in system studies. Collection of Labors. Vol. 10. - M.: All-Union Research Institute of System Research, 1982. P. 412.
20. Orlov A.I. Organizational and economic modeling: Tutorial: In 3 hours. Part 1: Non-Share Statistics. - M.: Publishing House MSTU. AD Bauman. - 2009. - 541 p.
21. Lutsenko E.V. Automated system-cognitive analysis in the management of active objects (system theory of information and its application in the study of economic, socio-psychological, technological and organizational and technical systems): monograph (scientific publication). -Srasnodar: Kubgu. 2002. - 605 p. http://elibrary.ru/item.asp?id\u003d18632909
1. Orlov A.I. Tochki Rosta Statisticheskih Metodov // Politematicheskij Setevoj Jelektronnyj Nauchnyj Zhurnal Kubanskogo Gosudarstvennogo Agraarnogo Universita. 2014. № 103. S. 136-162.
2. Kraskal DZH. Vzaimosvjaz "MEZHDU MNOGOMERNYM SHKALIROVANIEM I KLASTER-ANALIZOM // Klassifikacija I Klaster. M.: MIR, 1980. S.20-41.
3. Kruskal J.B., Wish M. Multidimensional Scaling // Sage University Paper Series: Qualitative Applications in The Social Sciences. 1978. №11.
4. Harman G. Sovremennyj Faktornyj Analiz. M.: Statistika, 1972. 489 s.
5. Orlov A.I. Zametki Po Teorii Klassifikacii. / Sociologija: Metodologija, Metody, Matematicheskie Modeli. 1991. No. 2. S.28-50.
6. Orlov A.I. Bazovye Rezul "Taty MatematicHeskoj Teorii Klassifikacii // Politematicheskij Setevoj Jelektronnyj Nauchnyj Zhurnal Kubanskogo Gosudarstvennogo AGRARNOGO Universiteta. 2015. № 110. S. 219-239.
7. Orlov A.I. Matematicheskie Metody Teorii Klassifikacii // Politematicheskij Setevoj Jelektronnyj Nauchnyj Zhurnal Kubanskogo Gosudarstvennogo Agrannogo Universita. 2014. № 95. S. 23 - 45.
8. Terehina A.Ju. Analiz Dannyh Metodami Mnogomernogo Shkalirovanija. - M.: Nauka, 1986. 168 s.
9. Perekrest v.T. NelineJNYJ Tipologicheskij Analiz Social "No-Jekonomicheskoj Informacii: Matematicheskie I Vychislitel" Nye Metody. - L.: Nauka, 1983. 176 s.
10. Tjurin ju.N., Litvak B.G., Orlov A.I., Satarov G.A., SHMERLING D.S. Analiz Nechislovoj Informacii. M.: Nauchnyj Sovet An SSSR Po Kompleksnoj Probleme "Kibernetika", 1981. - 80 s.
11. Orlov A.I. Obshhij vzgljad Na Statistiku OB # Ektov Nechislovoj Prirody // Analiz Nechislovoj Informacii V Sociologicheskih IsSledovanijah. - M.: Nauka, 1985. S.58-92.
12. Orlov A.I. Predel "NOE Raspredlenie Odnoj Ocenki Chisla Bazisnyh Funkcij v Regressii // Prikladnoj Mnogomernyj Statisticheskij Analiz. Uchenye Zapiski Po Statistike, T.33. - M.: Nauka, 1978. S.380-381.
13. Orlov A.I. Ocenka Razmernosti Modeli V Regressii // AlgoritMicheskoe I Programmnoe Obespechnie Prikladnogo StatistichesKogo Analiza. UChenye Zapiski Po Statistike, T.36. - M.: Nauka, 1980. S.92-99.
14. Orlov A.I. Asimptotika Nekotoryh Ocenok Razmernosti Modeli V Regressii // Prikladnaja Statistika. UChenye Zapiski Po Statistike, T.45. - M.: Nauka, 1983. S.260-265.
15. Orlov A.I. OB OCENIVANII REGRESSIONNOGO POLINOMA // Zavodskaja Laboratorija. Diagnostika Materialov. 1994. T.60. № 5. S.43-47.
16. Orlov A.I. NEKOTORYE VEROJATNOSTNYE VOPROSY TEORII Klassifikacii // Prikladnaja Statistika. UChenye Zapiski Po Statistike, T.45. - M.: Nauka, 1983. S.166-179.
17. Orlov A.I. On the Development of the Statistics of Nonnumerical Objects // Design of Experiments and Data Analysis: New Trends and Results. - M.: Antal, 1993. R.52-90.
18. Orlov A.I. Metody Snizhenija razmernosti // PRILOZHENIE 1 K Knige: Tolstova ju.N. Osnovy Mnogomernogo Shkalirovanija: Uchebnoe Posobie Dlja Vuzov. - M.: Izdatel "Stvo KDU, 2006. - 160 s.
19. Orlov A.I. Asimptotika reshenij jekstremal "nyh statisticheskih zadach // Analiz nechislovyh dannyh v sistemnyh issledovanijah Sbornik trudov Vyp.10 -... M .: Vsesojuznyj nauchno-issledovatel" skij institut sistemnyh issledovanij, 1982. S. 4-12.
20. Orlov A.I. Organizacionno-Jekonomicheskoe Modelirovanie: Uchebnik: V 3 CH. Chast "1: Nechislovaja Statistika. - M.: IZD-VO MgTU Im. N.je. Baumana. - 2009. - 541 s.
21. Lucenko E.V. Avtomatizirovannyj sistemno-kognitivnyj analiz v upravlenii aktivnymi ob # ektami (sistemnaja teorija informacii i ee primenenie v issledovanii jekonomicheskih, social "no-psihologicheskih, tehnologicheskih i organizacionno-tehnicheskih sistem): Monografija (nauchnoe izdanie) - Krasnodar:. KubGAU 2002. -. 605 s. Http://elibrary.ru/item.asp?id\u003d18632909
As a result of the study of the material of chapter 5, the student must:
know
- Basic concepts and tasks of lower dimension:
- Approaches to solving the problem of transformation of the feature space;
be able to
- use the method of the main component for the transition to standardized orthogonal features;
- evaluate the reduction of data informative when a decrease in the dimension of the feature space;
- solve the problem of constructing optimal multidimensional scales for researching objects;
own
- methods to reduce dimension to solve applied tasks of statistical analysis;
- Skills of interpretation of variables in a transformed signspace.
Basic concepts and tasks of lower dimension
At first glance than more information The objects of the study in the form of a set of characterizing their signs will be used to create a model, the better. However, excessive amount of information can lead to a decrease in the effectiveness of data analysis. There is even the term "curse of dimension" Curse of Dimensionality), characterizing problems of working with highly product data. With the need to reduce dimension in one form or another, the solution is associated with various statistical problems.
Non-informative features are an additional noise source and affect the accuracy of the valuation of the model parameters. In addition, data sets with a large number of features may contain groups of correlated variables. The presence of such signs of signs means duplicating information that can distort the specification of the model and affect the quality of its parameters. The higher the dimension of the data, the higher the volume of calculations during their algorithmic processing.
Two directions can be distinguished in reducing the dimension of the feature space on the principle of the variables used for this: selection of signs from the existing source set and the formation of new features by transformation of the initial data. In the ideal case, the abbreviated representation of the data must have dimension corresponding to the dimension, internally inherent data. INTRINSIC DIMENSIONALITY.
The search for the most informative features characterizing the studied phenomenon is an obvious direction of reducing the dimension of the problem that does not require the transformation of the source variables. This allows you to make a model more compact and avoid losses associated with the interfering effect of low-informative features. The selection of informative features is to find the best subset of many source variables. The criteria of the concept of "best" can serve or the most high quality Simulation with a given dimension of the feature space, or the smallest dimension of the data at which it is possible to build a model of the specified quality.
Direct solution to the task of creating best Model Related to the bust of all possible combinations of signs, which is usually excessively laborious. Therefore, as a rule, they resort to direct or reverse selection of signs. In direct selection procedures, a sequential addition of variables from the original set is made to achieve the desired quality of the model. In the algorithms of the consistent reduction of the original feature space (reverse selection), there is a phased removal of the least informative variables to the permissible reduction in the information content of the model.
It should be borne in mind that the informativeness of the signs is relative. The selection should ensure high informativeness of the set of features, and not the total informative of the components of its variables. Thus, the presence of correlation between signs reduces their overall informativeness due to the duplication of information common to them. Therefore, adding a new feature to the already selected ensures an increase in informativeness to the extent that it contains useful informationAbreparable in previously selected variables. The most simple is the situation of the selection of mutually orthogonal signs, in which the selection algorithm is very simple: the variables are ranked on informativeness, and the composition of the first signs in this ranking is used, which ensures specified informativeness.
The limited method of selection methods in order to reduce the dimension of space is associated with the assumption of the immediate presence of the necessary signs in the source data, which is usually incorrect. An alternative approach to a reduction in dimension provides for the conversion of features into a reduced set of new variables. Unlike the selection of the original signs, the formation of a new feature space involves the creation of new variables, which are usually functions of source signs. These variables directly observed are often called hidden, or latent. In the process of creating, these variables can be endowed with various useful properties, such as orthogonality. In practice, the initial signs are usually interrelated, therefore the transformation of their space to orthogonal generates new coordinates, in which there is no effect of duplicating information about the objects studied.
The display of objects in a new orthogonal feature space creates the ability to visually present the usefulness of each of the signs from the point of view of the differences between these objects. If the coordinates of the new basis are arranged by dispersion characterizing the range of values \u200b\u200bon them for the observations under consideration, it becomes obvious impossibility from a practical point of view of some features with small variables, since objects on these features are practically indistinguishable compared to their differences on more informative variables. In such a situation, we can talk about the so-called degeneration of the initial feature space from k. variables and the real dimension of this space t. may be less source (m< k.).
The reduction of the feature space is accompanied by a certain decrease in data information, but the level of permissible reduction can be determined in advance. The selection of features is projecting a set of source variables into a smaller dimension space. Compression of the feature space to two-three-dimensional can be useful for data visualization. Thus, the process of forming a new feature space usually leads to a smaller set of really informative variables. On their base, a better model can be built as based on a smaller number of the most informative features.
The formation of new variables based on the source is used for latent semantic analysis, data compression, classification and recognition of images, increase the speed and efficiency of learning processes. Compressed data is usually applied to further analysis and modeling.
One of the important applications for transformation of the feature space and reduce dimension is to build synthetic latent categories based on the measured signs of signs. These latent signs can characterize the general specific features of the phenomenon that integrate the private properties of the observed objects, which allows us to build integrated indicators of various levels of generalization of information.
The role of methods for the reduction of the feature space in the study of the problem of duplication of information in the initial signs, leading to the "swelling" of the dispersion of estimates of the coefficients of regression models, is essential. Transition to new, ideal case orthogonal and meaningful interpretable, variables is effective tool Modeling under the conditions of the multicollinearity of the source data.
The transformation of the initial feature space into orthogonal is convenient to solve the classification tasks, as it makes it possible to reasonably apply certain measures of proximity or differences in objects, such as Euclidean distance or the square of the Euclidean distance. In regression analysis, the construction of the regression equation on the main components allows to solve the problem of multicollinearity.
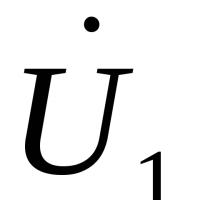 Magnetometry in the simplest version The ferrozond consists of a ferromagnetic core and two coils on it
Magnetometry in the simplest version The ferrozond consists of a ferromagnetic core and two coils on it Effective job search course search
Effective job search course search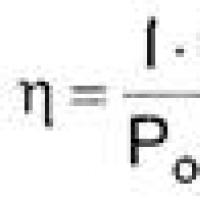 The main characteristics and parameters of the photodiode
The main characteristics and parameters of the photodiode How to edit PDF (five applications to change PDF files) How to delete individual pages from PDF
How to edit PDF (five applications to change PDF files) How to delete individual pages from PDF Why the fired program window is long unfolded?
Why the fired program window is long unfolded? DXF2TXT - export and translation of the text from AutoCAD to display a dwg traffic point in TXT
DXF2TXT - export and translation of the text from AutoCAD to display a dwg traffic point in TXT What to do if the mouse cursor disappears
What to do if the mouse cursor disappears