A Kálmán-szűrő alkalmazása GPS-koordináták sorozatának feldolgozásához. Kálmán szűrés Rádiós navigációs paraméterek kiértékelése a Kalman szűrő segítségével
Az interneten, így a Habré-n is, sok információt találhat a Kálmán-szűrőről. De maguknak a képleteknek nehéz könnyen emészthető származékát találni. Konklúzió nélkül mindezt a tudományt egyfajta sámánizmusként fogják fel, a képletek arctalan szimbólumkészletnek tűnnek, és ami a legfontosabb, sok egyszerű kijelentés, amely egy elmélet felszínén hever, felfoghatatlan. Ennek a cikknek az a célja, hogy a lehető legelérhetőbb nyelven beszéljen erről a szűrőről.
A Kalman-szűrő egy hatékony adatszűrő eszköz. Fő elve az, hogy a szűrés során magára a jelenség fizikájára vonatkozó információkat használjuk fel. Például, ha adatokat szűr egy autó sebességmérőjéből, akkor az autó tehetetlensége feljogosítja Önt arra, hogy a túl gyors sebességugrásokat mérési hibaként érzékelje. A Kálmán-szűrő azért érdekes, mert bizonyos értelemben ez a legjobb szűrő. Az alábbiakban részletesebben tárgyaljuk, mit is jelentenek pontosan a „legjobb” szavak. A cikk végén megmutatom, hogy sok esetben a képletek olyan mértékben leegyszerűsíthetők, hogy szinte semmi nem marad belőlük.
Oktatási program
A Kálmán-szűrővel való megismerkedés előtt azt javaslom, hogy idézzünk fel néhány egyszerű definíciót és tényt a valószínűségelméletből.
Véletlenszerű érték
Amikor azt mondják, hogy egy valószínűségi változó adott, akkor ez azt jelenti, hogy ez a mennyiség véletlenszerű értékeket vehet fel. Különböző értékeket vesz igénybe, eltérő valószínűséggel. Amikor mondjuk egy kockával dobsz, akkor egy diszkrét értékkészlet kiesik: Ha például egy vándorrészecske sebességéről van szó, akkor nyilvánvalóan folytonos értékkészlettel kell számolni. Egy valószínűségi változó "kiesett" értékeit a következővel fogjuk jelölni, de néha ugyanazt a betűt használjuk, amelyet egy valószínűségi változó jelölésére használunk:.
Folytonos értékhalmaz esetén a valószínűségi változót a valószínűségi sűrűség jellemzi, ami azt diktálja számunkra, hogy egyenlő a valószínűsége annak, hogy a valószínűségi változó egy hosszú pont kis környezetében "kiesik". Amint a képen látható, ez a valószínűség megegyezik a grafikon alatti árnyékolt téglalap területével:
Az életben gyakran előfordul, hogy a valószínűségi változók Gauss-féleek, ha a valószínűségi sűrűség egyenlő.
Látjuk, hogy a függvény harang alakú, középpontjában egy ponton és a sorrend jellegzetes szélességével rendelkezik.
Mivel Gauss-eloszlásról beszélünk, vétek lenne nem megemlíteni, honnan származik. Ahogy a számok szilárdan megalapozottak a matematikában, és a legváratlanabb helyeken fordulnak elő, úgy a Gauss-eloszlás is mélyen gyökerezett a valószínűségelméletben. Az egyik figyelemre méltó állítás, amely részben megmagyarázza a Gauss-féle mindenütt jelenlétet, a következő:
Legyen egy tetszőleges eloszlású valószínűségi változó (sőt, ennek az önkényességnek van néhány korlátozása, de ezek egyáltalán nem szigorúak). Végezzünk kísérleteket, és számítsuk ki a valószínűségi változó „kiesett” értékeinek összegét. Végezzünk sok ilyen kísérletet. Nyilvánvaló, hogy minden alkalommal más értékben kapjuk meg az összeget. Más szóval, ez az összeg maga is egy valószínűségi változó, és megvan a maga bizonyos eloszlási törvénye. Kiderült, hogy elég nagy esetén ennek az összegnek az eloszlási törvénye a Gauss-eloszláshoz igazodik (mellesleg a "harang" jellemző szélessége úgy nő). Bővebben a Wikipédiában: Central Limit Theorem. Az életben nagyon gyakran vannak olyan mennyiségek, amelyek nagyszámú egyenlő eloszlású független valószínűségi változóból állnak, ezért a Gauss-féle eloszlásúak.
Átlagos
Egy valószínűségi változó átlagértéke az, amit a határértékben kapunk, ha sok kísérletet végzünk, és kiszámítjuk a kiesett értékek számtani középértékét. Az átlagot többféleképpen jelölik: a matematikusok szeretik (elvárás), a külföldi matematikusok pedig (elvárás) jelölni. A fizikusok keresztül ill. Idegen módon fogjuk kijelölni:.
Például Gauss-eloszlás esetén az átlag az.
Diszperzió
A Gauss-eloszlás esetében jól látható, hogy a valószínűségi változó szívesebben esik ki az átlagértéke valamilyen közelébe. A grafikonon látható módon a sorrendi értékek jellemző szórása. Hogyan becsülhetjük meg egy tetszőleges valószínűségi változó értékeinek ezt a szórását, ha ismerjük az eloszlását? Megrajzolhatja a valószínűségi sűrűségét, és szemmel megbecsülheti a jellemző szélességet. De mi inkább az algebrai úton haladunk. Megtalálható az átlagtól való eltérés (modulus) átlagos hossza:. Ez az érték jó becslése lesz az értékek jellemző szórásának. De te és én nagyon jól tudjuk, hogy a modulok használata a képletekben egy fejtörést okoz, ezért ezt a képletet ritkán használják a jellemző terjedés becslésére.
Egy egyszerűbb (számítási szempontból egyszerű) módszer a megtalálás. Ezt az értéket variancianak nevezik, és gyakran nevezik. A variancia gyökerét szórásnak nevezzük. A szórás jó becslése egy valószínűségi változó terjedésének.
Például egy Gauss-eloszlásra kiszámíthatjuk, hogy a fent definiált variancia pontosan egyenlő, ami azt jelenti, hogy a szórása egyenlő, ami nagyon jól egyezik geometriai intuíciónkkal.
Valójában itt egy kis csalás van elrejtve. A helyzet az, hogy a Gauss-eloszlás definíciójában a kitevő alatt található a kifejezés. Ez a kettő a nevezőben pontosan azért van, hogy a szórása egyenlő legyen az együtthatóval. Vagyis maga a Gauss-eloszlási képlet egy speciálisan kiélezett formában van megírva, így figyelembe vesszük a szórását.
Független valószínűségi változók
A véletlen változók függőek és nem. Képzeld el, hogy egy tűt dobsz egy síkra, és felírod mindkét végének koordinátáit. Ez a két koordináta függő, összefügg azzal a feltétellel, hogy a köztük lévő távolság mindig egyenlő a tű hosszával, bár véletlenszerű értékek.
A valószínűségi változók függetlenek, ha közülük az első eredménye teljesen független a második eredményétől. Ha a valószínűségi változók függetlenek, akkor szorzatuk átlagértéke megegyezik átlagértékeik szorzatával:
Bizonyíték
Például a kék szem és az aranyéremmel végzett középiskola független valószínűségi változók. Ha kékszeműek mondjuk aranyérmesek, akkor kékszeműek. Ez a példa azt mutatja be, hogy ha a valószínűségi változókat a valószínűségi sűrűségükkel adjuk meg, akkor ezeknek az értékeknek a függetlensége abban fejeződik ki, hogy a valószínűségi sűrűség ( az első érték kiesett, a második) pedig a következő képlettel található:
Ebből rögtön az következik, hogy:
Mint látható, a bizonyítást olyan valószínűségi változókra hajtják végre, amelyeknek folyamatos az értékspektruma, és a valószínűségi sűrűségük adja meg őket. Más esetekben a bizonyítás gondolata hasonló.
Kálmán szűrő
A probléma megfogalmazása
Jelöljük a mérni kívánt értékkel, majd szűrjük. Ez lehet koordináta, sebesség, gyorsulás, páratartalom, bűz, hőmérséklet, nyomás stb.
Kezdjük egy egyszerű példával, amely elvezet bennünket egy általános probléma megfogalmazásához. Képzeljük el, hogy van egy rádióvezérlésű autónk, amely csak oda-vissza tud menni. Ismerve az autó tömegét, alakját, útfelületét stb., kiszámoltuk, hogy a vezérlő joystick hogyan befolyásolja a mozgás sebességét.
Ezután az autó koordinátája a törvény szerint megváltozik:
A való életben nem tudjuk számításainkban figyelembe venni az autóra ható apró zavarokat (szél, ütések, kavicsok az úton), így az autó valós sebessége eltér a számítotttól. A felírt egyenlet jobb oldalához egy valószínűségi változót adunk:
Nálunk egy írógépre van szerelve egy GPS szenzor, ami megpróbálja megmérni az autó valós koordinátáját, és természetesen nem tudja pontosan megmérni, de hibával méri, ami egyben egy valószínűségi változó is. Ennek eredményeként hibás adatokat kapunk az érzékelőtől:
A feladat az, hogy a hibás szenzorleolvasások ismeretében találjunk jó közelítést az autó valós koordinátájára.
Az általános feladat megfogalmazásában bármi felelős lehet a koordinátáért (hőmérséklet, páratartalom...), a rendszer kívülről történő vezérléséért felelős kifejezést pedig (a példában géppel) jelöljük. A koordináták és az érzékelők leolvasásának egyenletei így fognak kinézni:
Beszéljük meg részletesen, amit tudunk:
Érdemes megjegyezni, hogy a szűrési feladat nem élsimítási feladat. Nem az érzékelő adatait próbáljuk kisimítani, hanem a valós koordinátához legközelebb eső értéket.
Kálmán algoritmusa
Indukcióval fogunk vitatkozni. Képzeljük el, hogy a 3. lépésben már megtaláltuk a szenzor által szűrt értéket, ami jól közelíti a rendszer valódi koordinátáját. Ne felejtsük el, hogy ismerjük az ismeretlen koordináta változását szabályozó egyenletet:
ezért, még nem kapva az érzékelőtől kapott értéket, feltételezhetjük, hogy egy lépésben a rendszer ennek a törvénynek megfelelően fejlődik, és az érzékelő valami közeli értéket fog mutatni. Sajnos ennél pontosabbat egyelőre nem tudunk mondani. Másrészt egy lépésben pontatlan szenzorolvasás lesz a kezünkben.
Kálmán ötlete a következő. Ahhoz, hogy a valós koordinátához a legjobb közelítést kapjuk, a középutat kell választanunk egy pontatlan érzékelő leolvasása és a tőle elvárható előrejelzésünk között. Súlyozzuk az érzékelő leolvasását, és a súly az előre jelzett értéken marad:
Az együtthatót Kálmán-együtthatónak nevezik. Iterációs lépéstől függ, ezért helyesebb lenne megírni, de egyelőre, hogy ne zsúfoljuk össze a számítási képleteket, az indexét elhagyjuk.
A Kálmán-együtthatót úgy kell megválasztanunk, hogy a kapott optimális koordinátaérték a legközelebb álljon a valódihoz. Például, ha tudjuk, hogy az érzékelőnk nagyon pontos, akkor jobban megbízunk a leolvasásában, és nagyobb súlyt adunk az értéknek (egyhez közel). Ha az érzékelő éppen ellenkezőleg, teljesen pontatlan, akkor inkább az elméletileg előre jelzett értékre összpontosítunk.
Általában a Kalman-együttható pontos értékének megtalálásához csak minimálisra kell csökkentenie a hibát:
Az (1) egyenleteket használjuk (a mezőben lévők kék hátterűek), hogy átírjuk a hiba kifejezését:
Bizonyíték
Itt az ideje, hogy megvitassuk, mit jelent a hiba minimalizálása kifejezés? Végtére is, a hiba, mint láthatjuk, maga egy valószínűségi változó, és minden alkalommal más-más értéket vesz fel. Valójában nincs egy mindenkire érvényes megközelítés annak meghatározására, hogy mit jelent az, hogy a hiba minimális. Csakúgy, mint egy valószínűségi változó varianciája esetében, amikor a terjedésének jellemző szélességét próbáltuk megbecsülni, itt is a legegyszerűbb számítási kritériumot választjuk. Minimalizáljuk a négyzetes hiba átlagát:
Írjuk ki az utolsó kifejezést:
Bizonyíték
Abból a tényből, hogy a for kifejezésben szereplő összes valószínűségi változó független, az következik, hogy minden "kereszt" tag nulla:
Kihasználtuk azt a tényt, hogy akkor a varianciaképlet sokkal egyszerűbbnek tűnik:.
Ez a kifejezés minimális értéket vesz fel, ha (a deriváltot nullával egyenlővé tesszük):
Itt már írunk egy kifejezést a lépésindexű Kálmán-együtthatóra, ezzel hangsúlyozzuk, hogy az iterációs lépéstől függ.
A kapott optimális értéket behelyettesítjük a kifejezésbe, amit minimalizáltunk. Kapunk;
Feladatunkat teljesítettük. Kaptunk egy iteratív képletet a Kálmán-együttható kiszámításához.
Foglaljuk össze egy keretben megszerzett tudásunkat:
Példa
Matlab kód
Mindent kitöröl; N = 100%-os minták száma a = 0,1%-os gyorsulás sigmaPsi = 1 sigmaEta = 50; k = 1: N x = k x (1) = 0 z (1) = x (1) + normrnd (0, szigmaEta); t = 1 esetén: (N-1) x (t + 1) = x (t) + a * t + normrnd (0, sigmaPsi); z (t + 1) = x (t + 1) + normrnd (0, szigmaEta); vége; % kalman szűrő xOpt (1) = z (1); eOpt (1) = szigmaEta; t = 1 esetén: (N-1) eOpt (t + 1) = sqrt ((sigmaEta ^ 2) * (eOpt (t) ^ 2 + sigmaPsi ^ 2) / (sigmaEta ^ 2 + eOpt (t) ^ 2 + sigmaPsi ^ 2)) K (t + 1) = (eOpt (t + 1)) ^ 2 / sigmaEta ^ 2 xOpt (t + 1) = (xOpt (t) + a * t) * (1-K (t) +1)) + K (t + 1) * z (t + 1) vége; plot (k, xOpt, k, z, k, x)
Elemzés
Ha nyomon követjük, hogyan változik a Kálmán-együttható az iterációs lépéssel, akkor kimutatható, hogy mindig egy bizonyos értékig stabilizálódik. Például ha az érzékelő és a modell effektív hibája tíz az egyhez viszonyul egymáshoz, akkor a Kalman-együttható diagramja az iterációs lépéstől függően így néz ki:
A következő példában megvitatjuk, hogyan teheti ez sokkal könnyebbé az életünket.
Második példa
A gyakorlatban gyakran előfordul, hogy egyáltalán semmit sem tudunk a szűrés fizikai modelljéről. Például ki szeretné szűrni kedvenc gyorsulásmérőjének leolvasását. Nem tudja előre, hogy milyen törvény alapján kívánja elforgatni a gyorsulásmérőt. A legtöbb információ, amit megragadhat, az az érzékelő hibájának eltérése. Egy ilyen nehéz helyzetben a mozgásmodell minden tudatlansága egy valószínűségi változóba vezethető vissza:
De őszintén szólva egy ilyen rendszer egyáltalán nem teljesíti azokat a feltételeket, amelyeket a valószínűségi változóra támasztottunk, mert most ott van elrejtve minden számunkra ismeretlen mozgásfizika, ezért nem mondhatjuk, hogy a modell különböző időpontokban a hibák függetlenek egymástól, és átlagértékük nulla. Ebben az esetben a Kálmán-szűrőelmélet általában nem alkalmazható. De nem figyelünk erre a tényre, hanem ostobán alkalmazzuk a képletek összes kolosszát, szemre szabva az együtthatókat, hogy a szűrt adatok aranyosnak tűnjenek.
De választhatsz egy másik, sokkal egyszerűbb utat is. Ahogy fentebb láttuk, a Kálmán-együttható mindig egy érték felé stabilizálódik a növekedéssel. Ezért az együtthatók kiválasztása és a Kálmán-együttható komplex képletek segítségével történő meghatározása helyett tekinthetjük ezt az együtthatót mindig állandónak, és csak ezt az állandót választjuk. Ez a feltételezés szinte semmit sem ront el. Először is, már illegálisan használjuk Kálmán elméletét, másodszor pedig a Kálmán-együttható gyorsan konstanssá stabilizálódik. Ennek eredményeként minden nagyon leegyszerűsödik. Általában nincs szükségünk Kálmán elméletének képleteire, csak találnunk kell egy elfogadható értéket, és be kell illesztenünk az iteratív képletbe:
A következő grafikon egy kitalált érzékelő adatait mutatja két különböző módon szűrve. Feltéve, ha nem tudunk semmit a jelenség fizikájáról. Az első mód őszinte, Kálmán elméletének összes képletével. A második pedig leegyszerűsített, képletek nélkül.
Mint látjuk, a módszerek szinte azonosak. Kis különbség csak az elején figyelhető meg, amikor a Kálmán-együttható még nem stabilizálódott.
Vita
Amint láttuk, a Kalman-szűrő fő ötlete az, hogy olyan együtthatót találjunk, amely megfelel a szűrt értéknek
átlagosan ez különbözne a legkevésbé a koordináta valós értékétől. Láthatjuk, hogy a szűrt érték az érzékelő leolvasásának és az előző szűrt értéknek lineáris függvénye. Az előző szűrt érték pedig az érzékelő leolvasásának és az előző szűrt értéknek lineáris függvénye. És így tovább, amíg a lánc teljesen ki nem nyílik. Vagyis a szűrt érték attól függ mindenböl Az érzékelő korábbi leolvasásai lineárisan:
Ezért a Kalman-szűrőt lineáris szűrőnek nevezik.
Bizonyítható, hogy a Kalman szűrő a legjobb lineáris szűrők közül. A legjobb abban az értelemben, hogy a szűrőhiba átlagos négyzete minimális.
Többdimenziós eset
A Kálmán-szűrő egész elmélete általánosítható a többdimenziós esetre. Az ott található képletek kicsit ijesztőbbnek tűnnek, de a származtatásuk lényege ugyanaz, mint az egydimenziós esetben. Megtekintheti őket ebben a kiváló cikkben: http://habrahabr.ru/post/140274/.
És ebben a csodálatos videó- egy példát elemeznek ezek használatára.
A Wiener szűrők a legalkalmasabbak a feldolgozási folyamatokhoz vagy általában a folyamatok szakaszaihoz (blokk feldolgozás). A szekvenciális feldolgozáshoz minden órajel ciklusban a jel aktuális becslése szükséges, figyelembe véve a megfigyelési folyamat során a szűrőbemenetre érkező információkat.
A Wiener-szűréssel minden új jelmintához újra kell számítani az összes szűrősúlyt. Jelenleg elterjedtek az adaptív szűrők, amelyekben a beérkező új információkkal folyamatosan korrigálják a korábban elvégzett jelértékelést (radarban célkövetés, vezérlésben automatikus vezérlőrendszerek stb.). Különösen érdekesek a Kalman-szűrőként ismert rekurzív típusú adaptív szűrők.
Ezeket a szűrőket széles körben használják az automatikus szabályozási és vezérlőrendszerek vezérlőhurkaiban. Innen jelentek meg, ezt bizonyítja az a sajátos terminológia, amellyel munkájukat állapottérként írták le.
A neurális számítástechnika gyakorlatában az egyik fő megoldandó feladat a neurális hálózatok tanulására szolgáló gyors és megbízható algoritmusok beszerzése. Ebből a szempontból hasznos lehet lineáris szűrők használata a visszacsatoló hurokban. Mivel a betanító algoritmusok iteratív jellegűek, egy ilyen szűrőnek szekvenciális rekurzív becslőnek kell lennie.
Paraméterbecslési probléma
A statisztikai döntések elméletének egyik nagy gyakorlati jelentőségű problémája a rendszerek állapotvektorainak és paramétereinek becslésének problémája, amelyet a következőképpen fogalmazunk meg. Tegyük fel, hogy meg kell becsülni a $ X $ vektorparaméter értékét, amely nem érhető el közvetlen méréssel. Ehelyett egy másik $ Z $ paraméter mérése történik, a $ X $ függvényében. A becslési probléma a kérdés megválaszolása: mit lehet mondani $ X $-ról $ Z $ ismeretében. Általános esetben a $ X $ vektor optimális kiértékelésének eljárása az értékelés minőségének elfogadott kritériumától függ.
Például a paraméterbecslés problémájának Bayes-féle megközelítése teljes a priori információt igényel a becsült paraméter valószínűségi tulajdonságairól, ami gyakran lehetetlen. Ezekben az esetekben a legkisebb négyzetek (OLS) módszeréhez folyamodnak, amely sokkal kevesebb előzetes információt igényel.
Tekintsük az OLS alkalmazását arra az esetre, amikor a $ Z $ megfigyelési vektort lineáris modellel viszonyítjuk a $ X $ paraméterbecslési vektorhoz, és a megfigyelés $ V $ zajt tartalmaz, amely nem korrelál a becsült paraméterrel:
$ Z = HX + V $, (1)
ahol $ H $ egy transzformációs mátrix, amely leírja a megfigyelt mennyiségek és a becsült paraméterek közötti kapcsolatot.
A négyzetes hibát minimalizáló $ X $ becslés a következőképpen írható:
$ X_ (оц) = (H^TR_V^ (-1) H)^ (-1) H^TR_V^ (-1) Z $, (2)
A $ V $ zaj ne legyen korrelálva, ebben az esetben a $ R_V $ mátrix csak az azonosságmátrix, és a becslési egyenlet egyszerűbbé válik:
$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $, (3)
A mátrix formátumú írás nagymértékben megtakarítja a papírt, de egyesek számára szokatlan lehet. A következő példa, amelyet Yu. M. Korshunov monográfiájából, „A kibernetika matematikai alapjai” című monográfiájából vettünk, mindezt szemlélteti.
A következő elektromos áramkör áll rendelkezésre:
A megfigyelt értékek ebben az esetben a készülékek leolvasásai $ A_1 = 1 A, A_2 = 2 A, V = 20 B $.
Ezenkívül ismert az ellenállás $ R = 5 $ Ohm. A hiba minimális középnégyzetének kritériuma szempontjából a legjobb módon meg kell becsülni a $ I_1 $ és a $ I_2 $ áramok értékét. A legfontosabb dolog itt az, hogy van valamilyen kapcsolat a megfigyelt értékek (műszer leolvasások) és a becsült paraméterek között. És ezt az információt kívülről hozzák be.
Ebben az esetben ezek a Kirchhoff-törvények, a szűrés esetében (amelyről a továbbiakban lesz szó) - egy idősor autoregresszív modellje, amely feltételezi az aktuális érték függőségét az előzőektől.
Tehát a Kirchhoff-törvények ismerete, amelynek semmi köze a statisztikai döntések elméletéhez, lehetővé teszi a megfigyelt értékek és a becsült paraméterek közötti kapcsolat létrehozását (aki tanult elektrotechnikát - ellenőrizheti, a többinek szót fogadni):
$$ z_1 = A_1 = I_1 + \ xi_1 = 1 $$
$$ z_2 = A_2 = I_1 + I_2 + \ xi_2 = 2 $$
$$ z_2 = V / R = I_1 + 2 * I_2 + \ xi_3 = 4 $$
Ez vektor formában van:
$$ \ kezdődik (vmátrix) z_1 \\ z_2 \\ z_3 \ end (vmátrix) = \ kezdődik (vmátrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmátrix) \ kezdődik (vmátrix) I_1 \ \ I_2 \ end (vmátrix) + \ kezd (vmátrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmátrix) $$
Vagy $ Z = HX + V $, ahol
$$ Z = \ kezdődik (vmátrix) z_1 \\ z_2 \\ z_3 \ end (vmátrix) = \ kezdődik (vmátrix) 1 \\ 2 \\ 4 \ end (vmátrix); H = \ kezdődik (vmátrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmátrix); X = \ kezdődik (vmátrix) I_1 \\ I_2 \ end (vmátrix); V = \ kezdete (vmátrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ vége (vmátrix) $$
Figyelembe véve az egymással nem korrelált interferencia értékeit, megkapjuk az I 1 és I 2 becslését a legkisebb négyzetek módszerével a 3. képlet szerint:
$ H ^ TH = \ kezdődik (vmátrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmátrix) \ kezdődik (vmátrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmátrix) = \ kezdődik (vmátrix) 3 & 3 \\ 3 & 5 \ end (vmátrix); (H ^ TH) ^ (- 1) = \ frac (1) (6) \ kezdődik (vmátrix) 5 & -3 \\ -3 & 3 \ end (vmátrix) $;
$ H ^ TZ = \ kezdődik (vmátrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmátrix) \ kezdődik (vmátrix) 1 \\ 2 \\ 4 \ end (vmátrix) = \ begin (vmátrix) 7 \ \ \ 10 \ vége (vmátrix); X (ots) = \ frac (1) (6) \ kezdődik (vmátrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) \ begin (vmatrix) 7 \\ 10 \ end (vmatrix) = \ frac (1) (6) \ kezdődik (vmátrix) 5 \\ 9 \ end (vmátrix) $;
Tehát $ I_1 = 5/6 = 0,833 A $; $ I_2 = 9/6 = 1,5 A $.
Szűrési feladat
Ellentétben a fix értékű paraméterek becslésének problémájával, a szűrés problémájában meg kell becsülni a folyamatokat, vagyis meg kell találni egy időben változó, zaj által torzított jel aktuális becslését. , nem érhető el a közvetlen méréshez. Általában a szűrési algoritmusok típusa a jel és a zaj statisztikai tulajdonságaitól függ.
Feltételezzük, hogy a hasznos jel az idő lassan változó függvénye, az interferencia pedig nem korrelált zaj. A legkisebb négyzetek módszerét fogjuk alkalmazni, ismét a jel és az interferencia valószínűségi jellemzőiről szóló előzetes információ hiánya miatt.
Először becslést kapunk $ x_n $ aktuális értékére a $ z_n, z_ (n-1), z_ (n-2) \ dots z_ idősor legújabb értékeinek $ k $ rendelkezésre álló $ k $ alapján. (n- (k-1)) $. A megfigyelési modell ugyanaz, mint a paraméterbecslési feladatnál:
Nyilvánvaló, hogy a $ Z $ egy oszlopvektor, amely a $ z_n, z_ (n-1), z_ (n-2) \ pontok z_ (n- (k-1)) idősorok megfigyelt értékeiből áll. $, $ V $ - vektor-zajoszlop $ \ xi _n, \ xi _ (n-1), \ xi_ (n-2) \ pontok \ xi_ (n- (k-1)) $, amely torzítja az igazat jel. Mit jelentenek a $ H $ és a $ X $ szimbólumok? Miről beszélhetünk például a $ X $ oszlopvektorról, ha csak becslést kell adni az idősor aktuális értékére? És egyáltalán nem világos, hogy mit kell érteni a $ H $ transzformációs mátrix alatt.
Mindezekre a kérdésekre csak akkor lehet választ adni, ha figyelembe vesszük a jelgeneráló modell koncepcióját. Vagyis szükség van az eredeti jel valamilyen modelljére. Ez érthető, a jel és az interferencia valószínűségi jellemzőiről szóló előzetes információ hiányában már csak a feltételezések maradnak hátra. Nevezhetjük jóslásnak a kávézaccon, de a szakértők más terminológiát preferálnak. A "hajszárítójukon" paraméteres modellnek hívják.
Ebben az esetben ennek a konkrét modellnek a paramétereit becsüljük meg. A megfelelő jelgenerálási modell kiválasztásakor ne feledje, hogy a Taylor sorozatban bármely elemző funkció bővíthető. A Taylor-sorozat elképesztő tulajdonsága, hogy egy függvény alakját tetszőleges $ t $ távolságban egy $ x = a $ ponttól egyedileg határozza meg a függvény viselkedése a $ x = a pont végtelenül kis környezetében. $ (az első és magasabb rendű származékairól beszélünk).
Így a Taylor sorozat létezése azt jelenti, hogy az analitikus függvény belső szerkezete nagyon erős csatolással rendelkezik. Ha például a Taylor sorozat három tagjára korlátozzuk magunkat, akkor a jelgenerálási modell így fog kinézni:
$ x_ (n-i) = F _ (- i) x_n $, (4)
$$ X_n = \ kezdődik (vmátrix) x_n \\ x "_n \\ x" "_ n \ end (vmátrix); F _ (- i) = \ kezdődik (vmátrix) 1 & -i & i ^ 2/2 \\ 0 & 1 & -i \\ 0 & 0 & 1 \ end (vmátrix) $$
Vagyis a 4-es képlet a polinom adott sorrendjére (a példában 2) kapcsolatot hoz létre a jel $ n $ -edik értéke az időszekvenciában és a $ (n-i) $ -edik értéke között. Így a becsült állapotvektor ebben az esetben a tényleges becsült értéken kívül tartalmazza a jel első és második deriváltját is.
Az automatikus vezérlés elméletében egy ilyen szűrőt másodrendű asztatizmusszűrőnek neveznék. A $ H $ transzformációs mátrix erre az esetre (a becslés az aktuális és $ k-1 $ korábbi minták alapján történik) így néz ki:
$$ H = \ begin (vmátrix) 1 & -k & k ^ 2/2 \\ - & - & - \\ 1 & -2 & 2 \\ 1 & -1 & 0,5 \\ 1 & 0 & 0 \ vége (vmátrix) $$
Mindezek a számok a Taylor-sorból származnak, feltéve, hogy a szomszédos megfigyelt értékek közötti időintervallum állandó és egyenlő 1-gyel.
Tehát a szűrési feladat feltételezéseink szerint a paraméterek becslésének feladatára redukálódott; ebben az esetben az elfogadott jelgeneráló modell paramétereit becsüljük meg. És a $ X $ állapotvektor értékeinek becslése ugyanazon 3 képlet szerint történik:
$$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $$
Lényegében egy paraméteres becslési eljárást valósítottunk meg, amely a jelgenerálási folyamat autoregresszív modelljén alapul.
A 3. képlet könnyen megvalósítható programozottan, ehhez ki kell tölteni a $ H $ mátrixot és a $ Z $ megfigyelések vektoroszlopát. Ezeket a szűrőket ún véges memóriaszűrők, mivel az utolsó $ k $ megfigyeléseket használják a $ X_ (nоц) $ aktuális becsléséhez. Minden új megfigyelési ciklusnál egy újat adunk az aktuális megfigyelésekhez, és a régit eldobjuk. Az osztályzatszerzésnek ezt a folyamatát ún elhúzható ablak.
Növekvő memóriaszűrők
A véges memóriával rendelkező szűrőknek az a fő hátrányuk, hogy minden új megfigyelés után újra el kell végezni a memóriában tárolt összes adat teljes újraszámítását. Ezenkívül a becslések számítása csak az első $ k $ megfigyelések eredményeinek összesítése után kezdhető meg. Vagyis ezeknek a szűrőknek hosszú az átmeneti ideje.
Ennek a hátránynak a leküzdéséhez át kell váltani az állandó memóriaszűrőről a szűrőre növekvő memória... Egy ilyen szűrőben a megfigyelt értékek számának, amelyre a becslés készül, egybe kell esnie az aktuális megfigyelés n számával. Ez lehetővé teszi, hogy becsléseket kapjunk a $ X $ becsült vektor komponenseinek számával megegyező megfigyelések számából. Ezt pedig az átvett modell sorrendje határozza meg, vagyis hogy a Taylor sorozatból hány kifejezést használnak a modellben.
Ugyanakkor az n növekedésével javulnak a szűrő simítási tulajdonságai, vagyis nő a becslések pontossága. Ennek a megközelítésnek a közvetlen megvalósítása azonban a számítási költségek növekedésével jár. Ezért a növekvő memóriaszűrőket úgy valósítják meg visszatérő.
A helyzet az, hogy n-re már van egy $ X _ ((n-1) оц) $ becslésünk, amely az összes korábbi megfigyelésről tartalmaz információt $ z_n, z_ (n-1), z_ (n-2) \ pontok z_ (n- (k-1)) $. A $ X_ (nоц) $ becslést a következő $ z_n $ megfigyelésből kapjuk a $ X _ ((n-1)) (\ mbox (оц)) $ becslésben tárolt információk felhasználásával. Ezt az eljárást ismétlődő szűrésnek nevezik, és a következőkből áll:
- becslés szerint $ X _ ((n-1)) (\ mbox (оц)) $ megjósolni $ X_n $ becslését a 4. képlet szerint $ i = 1 $: $ X _ (\ mbox (nоtsapriori)) = F_1X _ ((n-1 ) sc) $. Ez egy előzetes becslés;
- a jelenlegi megfigyelés eredményei szerint $ z_n $ ezt az a priori becslést igazzá, azaz a posteriori konvertálják;
- ez az eljárás minden lépésnél megismétlődik, kezdve $ r + 1 $-tól, ahol $ r $ a szűrő sorrendje.
Az ismétlődő szűrés végső képlete így néz ki:
$ X _ ((n-1) оц) = X _ (\ mbox (nоtsapriori)) + (H ^ T_nH_n) ^ (- 1) h ^ T_0 (z_n - h_0 X _ (\ mbox (nоtsapriori))) $ , (6)
hol található a második sorrendű szűrőnk:
A Formula 6-on alapuló növekvő memóriaszűrő a Kálmán-szűrőként ismert szűrési algoritmus speciális esete.
Ennek a képletnek a gyakorlati megvalósítása során emlékezni kell arra, hogy a benne foglalt a priori becslést a 4. képlet határozza meg, és a $ h_0 X _ (\ mbox (notspriori)) $ érték a $ X vektor első komponense. _ (\ mbox (notspriori)) $.
A növekvő memóriaszűrőnek van egy fontos tulajdonsága. Ha a 6-os képletet nézzük, akkor a végeredmény a megjósolt pontszámvektor és a javító tag összege. Ez a korrekció nagy kis $ n $ esetén, és csökken $ n $ növekedésével, és nullára hajlik: $ n \ rightarrow \ infty $. Vagyis az n növekedésével a szűrő simító tulajdonságai nőnek, és a benne rejlő modell kezd dominálni. De a valós jel csak bizonyos területeken felelhet meg a modellnek, ezért az előrejelzés pontossága romlik.
Ennek leküzdésére néhány n $-tól kezdődően tiltják a korrekciós időtartam további csökkentését. Ez egyenértékű a szűrő sávszélességének változtatásával, azaz kicsi n esetén a szűrő szélesebb (kevésbé tehetetlen), nagy n esetén pedig inerciálisabbá válik.
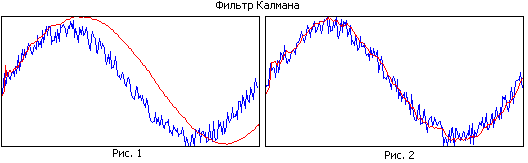
Hasonlítsa össze az 1. és 2. ábrát. Az első ábrán a szűrő nagy memóriával rendelkezik, miközben jól simít, de a keskeny sáv miatt a becsült pálya elmarad a valóstól. A második ábrán a szűrőmemória kisebb, rosszabbul simít, de jobban követi a valós pályát.
Irodalom
- YM Korshunov "A kibernetika matematikai alapjai"
- A.V. Balakrishnan "Kalman szűrési elmélet"
- VNFomin "Ismétlődő becslés és adaptív szűrés"
- C.F.N. Cowen, P.M. "Adaptív szűrők" engedélyezése
Ezt a szűrőt különféle területeken használják - a rádiótechnikától a közgazdaságtanig. Itt megvitatjuk ennek a szűrőnek a fő gondolatát, jelentését, lényegét. A lehető legegyszerűbb módon kerül bemutatásra.
Tegyük fel, hogy szükségünk van egy objektum bizonyos mennyiségeinek mérésére. A rádiótechnikában leggyakrabban egy bizonyos eszköz (érzékelő, antenna stb.) kimenetén lévő feszültség mérésével foglalkoznak. Az elektrokardiográfos példában (lásd) az emberi test biopotenciáljának mérésével foglalkozunk. A közgazdaságtanban például árfolyamok lehetnek a mért érték. Minden nap más az árfolyam, pl. minden nap más értéket adnak az „ő mérései”. És ha általánosítani akarunk, akkor azt mondhatjuk, hogy az ember tevékenységének nagy része (ha nem is az összes) pontosan bizonyos mennyiségek állandó mérésére-összehasonlítására redukálódik (lásd a könyvet).
Tehát tegyük fel, hogy folyamatosan mérünk valamit. Tételezzük fel azt is, hogy a méréseink mindig valamilyen hibával járnak – ez érthető is, hiszen nincs ideális mérőműszer, és mindegyik hibás eredményt ad. A legegyszerűbb esetben a leírtak a következő kifejezésre redukálhatók: z = x + y, ahol x az a valós érték, amit mérni akarunk, és ami mérhető lenne, ha lenne ideális mérőeszközünk, y a a mérőeszköz által bevezetett mérési hiba, és z - az általunk mért érték. A Kálmán-szűrő feladata tehát az, hogy a mért z-ből kitalálja (meghatározza), de mi volt x valódi értéke, amikor megkaptuk a z-ünket (amiben a valódi érték és a mérési hiba "ül"). Ki kell szűrni (kigyomlálni) az x valódi értékét z-ből - el kell távolítani az y torzító zajt z-ből. Azaz, ha csak az összeg van kéznél, meg kell találnunk, hogy mely feltételek adták ezt az összeget.
A fentiek fényében most mindent a következőképpen fogunk megfogalmazni. Tegyük fel, hogy csak két véletlen szám van. Csak az összegüket adjuk meg, és ebből az összegből kell meghatároznunk a feltételeket. Például megkaptuk a 12-es számot, és azt mondják: 12 az x és y számok összege, a kérdés az, hogy x és y mivel egyenlő. A kérdés megválaszolásához összeállítjuk az egyenletet: x + y = 12. Egy egyenletet kaptunk két ismeretlennel, ezért szigorúan véve nem lehet találni két olyan számot, amely ezt az összeget adta. De ezekről a számokról mégis mondhatunk valamit. Azt mondhatjuk, hogy ez vagy az 1 és 11, vagy 2 és 10, vagy 3 és 9, vagy 4 és 8 stb., vagy 13 és -1, vagy 14 és -2, vagy 15 és - 3 stb. Azaz az összegből (példánkban 12) meg tudjuk határozni a lehetséges opciók halmazát, amelyek összege pontosan 12. Ezen opciók egyike az általunk keresett pár, amely jelenleg 12-t adott. azt is érdemes megjegyezni, hogy az összesen 12-t adó számpárok összes változata az 1. ábrán látható egyenest alkot, amelyet az x + y = 12 (y = -x + 12) egyenlet ad meg.
1. ábra
Így a keresett pár valahol ezen az egyenesen fekszik. Ismétlem, ezek közül a lehetőségek közül lehetetlen kiválasztani azt a párt, amely valójában volt - amely a 12-es számot adta, anélkül, hogy bármilyen további nyoma lenne. De, abban a helyzetben, amelyre a Kálmán-szűrőt kitalálták, vannak ilyen tippek... Valamit előre tudni lehet a véletlen számokról. Ott különösen ismert az egyes számpárok úgynevezett eloszlási hisztogramja. Általában ezeknek a nagyon véletlen számoknak az előfordulásának meglehetősen hosszú megfigyelése után kapjuk meg. Azaz például tapasztalatból ismert, hogy az esetek 5%-ában általában egy x = 1, y = 8 pár esik ki (ezt a párt jelöljük: (1,8)), 2%-ban egy pár. x = 2, y = 3 ( 2,3), az esetek 1%-ában egy pár (3,1), az esetek 0,024%-ában egy pár (11,1) stb. Ez a hisztogram ismét be van állítva minden pár számára számok, beleértve azokat is, amelyek összesen 12-t alkotnak. Így minden párra, amely összesen 12-t ad, azt mondhatjuk, hogy például egy (1, 11) pár az esetek 0,8%-ában esik ki, egy pár ( 2, 10) - az esetek 1%-ában, egy pár (3, 9) - az esetek 1,5%-ában stb. Így a hisztogram segítségével meghatározhatjuk, hogy az esetek hány százalékában egy pár tagjának összege 12. Tegyük fel például, hogy az esetek 30%-ában az összeg 12. A fennmaradó 70%-ban pedig a maradék párok esnek. ki - ezek (1,8), (2, 3), (3,1) stb. - azok, amelyek összeadják a 12-től eltérő számokat. És például egy pár (7,5) essen ki az esetek 27%-ában, míg az összes többi pár, amely összeadja a 12-t, 0,024% + 0,8% + 1% -ban. + 1,5% +… = az esetek 3%-a. Így a hisztogram alapján azt találtuk, hogy az összesen 12-t adó számok az esetek 30%-ában kiesnek. Ugyanakkor tudjuk, hogy ha 12 esett, akkor ennek leggyakrabban (a 30%-a 27%-ában) a pár (7,5) az oka. Vagyis ha már Kigurult 12-nél azt mondhatjuk, hogy 90%-ban (30%-ból 27% - vagy ami minden 30-ból 27-szer ugyanaz) a 12-es kidobásának oka egy pár (7,5). Tudva, hogy a 12-vel egyenlő összeg megszerzésének oka leggyakrabban a (7,5) pár, logikusan feltételezhető, hogy nagy valószínűséggel most esett ki. Persze továbbra sem tény, hogy valójában most a 12-es számot ez a bizonyos pár alkotja, de legközelebb, ha 12-vel találkozunk, és ismét a (7,5) párt feltételezzük, akkor valahol az esetek 90%-ában 100%-ból igazunk lesz. De ha feltételezzük a (2, 10) párost, akkor az esetek 30%-ából csak 1%-ban lesz igazunk, ami 3,33% helyes tipp, szemben a 90%-kal, ha a (7,5) párt feltételezzük. Ez minden – ez a Kalman-szűrő algoritmus lényege. Vagyis a Kálmán-szűrő nem garantálja, hogy nem hibázik az összegző meghatározásakor, de garantálja, hogy a minimális számú alkalommal hibázik (a hiba valószínűsége minimális lesz), mivel statisztikákat használ - hiányzó számpárok hisztogramja. Azt is hangsúlyozni kell, hogy a Kálmán-szűrési algoritmusban gyakran használják az úgynevezett valószínűségi eloszlási sűrűséget (PDF). Meg kell értenie azonban, hogy a jelentése ugyanaz, mint a hisztogramé. Ezenkívül a hisztogram egy PDF-alapú függvény, és annak közelítése (lásd például).
Ezt a hisztogramot elvileg két változó függvényében is ábrázolhatjuk - vagyis az xy sík feletti felületként. Ahol magasabb a felület, ott nagyobb a valószínűsége a megfelelő párnak. A 2. ábra egy ilyen felületet mutat be.

2. ábra
Mint látható az x + y = 12 egyenes felett (amelyben összesen 12 párra van lehetőség), a felületi pontok különböző magasságokban és a legmagasabb magasságban helyezkednek el a (7,5) koordinátákkal rendelkező opciónál. És amikor 12-vel egyenlő összeggel találkozunk, az esetek 90%-ában ennek az összegnek az oka pontosan a (7,5) pár. Azok. ennek a párnak, amely összesen 12-t ad, a legnagyobb az előfordulási valószínűsége, feltéve, hogy az összeg 12.
Így a Kálmán-szűrő mögött meghúzódó gondolatot itt ismertetjük. Erre épül mindenféle módosítás - egylépcsős, többlépcsős visszatérő stb. A Kalman-szűrő mélyebb tanulmányozására ajánlom a Van Tries G. Theory of detection, estimation and modulation című könyvet.
p.s. Azok számára, akik érdeklődnek a matematika fogalmainak elmagyarázása iránt, az úgynevezett „ujjakon”, tanácsot adhat ehhez a könyvhöz, és különösen a „Matematika” rész fejezeteihez (magát a könyvet vagy egyes fejezeteit megvásárolhatja azt).
A Random Forest az egyik kedvenc adatbányászati algoritmusom. Először is, hihetetlenül sokoldalú, regressziós és osztályozási problémák megoldására egyaránt használható. Anomáliák keresése és előrejelzők kiválasztása. Másodszor, ez egy olyan algoritmus, amelyet nagyon nehéz helytelenül alkalmazni. Egyszerűen azért, mert más algoritmusokkal ellentétben kevés konfigurálható paramétere van. Alapjában véve is meglepően egyszerű. És ugyanakkor figyelemre méltó a precizitása.
Mi az ötlet egy ilyen csodálatos algoritmus mögött? Az ötlet egyszerű: mondjuk van valami nagyon gyenge algoritmusunk. Ha sok különböző modellt készítünk ezzel a gyenge algoritmussal, és átlagoljuk az előrejelzéseik eredményét, akkor a végeredmény sokkal jobb lesz. Ez az úgynevezett ensemble training in action. A Random Forest algoritmust ezért "Véletlen erdőnek" nevezik, mivel a kapott adatokhoz számos döntési fát hoz létre, majd átlagolja előrejelzéseik eredményét. Itt fontos szempont a véletlenszerűség eleme az egyes fák létrehozásában. Hiszen világos, hogy ha sok egyforma fát hozunk létre, akkor az átlagolásuk eredménye egy fa pontossága lesz.
Hogyan működik? Tegyük fel, hogy van néhány bemeneti adatunk. Minden oszlop valamilyen paraméternek, minden sor valamilyen adatelemnek felel meg.
A teljes adatkészletből véletlenszerűen kiválaszthatunk bizonyos számú oszlopot és sort, és ezek alapján döntési fát építhetünk.

2012. május 10. csütörtök
2012. január 12. csütörtök

Ez minden. A 17 órás repülés véget ért, Oroszország maradt a tengerentúlon. Egy hangulatos, 2 hálószobás San Francisco-i lakás ablakán keresztül a híres kaliforniai Szilícium-völgy néz ránk. Igen, ez az oka annak, hogy mostanában gyakorlatilag nem írtam. Költöztünk.
Az egész 2011 áprilisában kezdődött, amikor telefonos interjút készítettem a Zyngánál. Akkor az egész valami játéknak tűnt, aminek semmi köze a valósághoz, és el sem tudtam képzelni, hogy ennek mi lesz az eredménye. 2011 júniusában Zynga Moszkvába érkezett és interjúsorozatot készített, körülbelül 60 telefonos interjún átesett jelöltet vettek figyelembe, és közülük körülbelül 15-öt választottak ki (nem tudom a pontos számot, valaki később meggondolta magát, valaki azonnal visszautasította). Az interjú meglepően egyszerűnek bizonyult. Nincsenek programozási feladatok, nincsenek trükkös kérdések a sraffozások formájával kapcsolatban, leginkább a chatelhetőséget tesztelték. A tudást pedig véleményem szerint csak felületesen értékelték.
És akkor kezdődött a trükk. Először megvártuk az eredményeket, majd az ajánlatot, majd az LCA jóváhagyását, majd a vízumkérelem jóváhagyását, majd az USA-ból érkező dokumentumokat, majd a sorban állást a nagykövetségen, majd egy kiegészítő ellenőrzést, majd a Vízum. Időnként úgy tűnt számomra, hogy készen állok mindent eldobni és gólt szerezni. Időnként kételkedtem, hogy kell-e nekünk ez az Amerika, elvégre Oroszországban sem rossz. Az egész folyamat körülbelül hat hónapig tartott, ennek eredményeként december közepén megkaptuk a vízumot és elkezdtük az indulásra való felkészülést.
Hétfő volt az első munkanapom. Az irodában minden feltétel adott nem csak a munkához, hanem az élethez is. Reggeli, ebéd és vacsora saját szakácsainktól, egy csomó változatos étel mindenhol összezsúfolva, edzőterem, masszázs és még fodrászat is. Mindez a dolgozók számára teljesen ingyenes. Sokan biciklivel jutnak munkába, és több helyiség is van a járművek tárolására. Általában még soha nem találkoztam ilyesmivel Oroszországban. Mindennek azonban megvan a maga ára, azonnal figyelmeztettek minket, hogy sokat kell dolgoznunk. Számomra nem egészen világos, hogy az ő mércéjük szerint mi a "sok".
Remélhetőleg azonban a rengeteg munka ellenére belátható időn belül folytathatom a blogírást, és talán elmondhatok valamit az amerikai életről és programozói munkáról Amerikában. Várj és láss. Addig is gratulálok mindenkinek a közelgő újévhez és karácsonyhoz, és hamarosan találkozunk!
Felhasználási példaként kinyomtatjuk az orosz cégek osztalékhozamát. Alapárnak a részvény nyilvántartás zárásának napján érvényes záróárát vesszük. Valamilyen oknál fogva ez az információ nem a trojka webhelyén található, de sokkal érdekesebb, mint az osztalék abszolút értéke.
Figyelem! A kód végrehajtása hosszú ideig tart, mert minden promócióhoz kérést kell küldenie a finam szervereknek, és meg kell kapnia az értékét.
Eredmény<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0) (próbáld meg ((idézetek<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0) (nn<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

Hasonlóképpen készíthet statisztikákat az elmúlt évekről.
Valahogy úgy történt, hogy nagyon szeretek mindenféle algoritmust, amelyeknek világos és logikus matematikai indoklása van) De gyakran az interneten található leírásuk annyira túlterhelt képletekkel és számításokkal, hogy egyszerűen lehetetlen megérteni az algoritmus általános jelentését. De egy eszköz / mechanizmus / algoritmus lényegének és működési elvének megértése sokkal fontosabb, mint a hatalmas képletek memorizálása. Bármilyen elcsépelt is, a több száz képlet memorizálása sem segít semmit, ha nem tudod, hogyan és hol alkalmazd őket -val a gyakorlatban. Igyekszem nem túlterhelni a matematikai számításokkal, hogy tiszta legyen az anyag és könnyű legyen az olvasás.
És ma erről fogunk beszélni Kálmán szűrő, derítsük ki, mi ez, miért és hogyan használják.
Kezdjük egy kis példával. Álljunk szemben egy repülő repülőgép koordinátájának meghatározásával. Sőt, természetesen a koordinátát (jelöljük ki) a lehető legpontosabban kell meghatározni. 
A repülőn előre telepítettünk egy szenzort, ami megadja a kívánt helyadatokat, de mint minden ezen a világon, a szenzorunk sem tökéletes. Ezért érték helyett a következőket kapjuk:
hol van a szenzorhiba, vagyis egy valószínűségi változó. Így a mérőberendezés pontatlan leolvasásaiból a repülőgép valós helyzetéhez lehető legközelebb eső koordinátaértéket () kell megkapnunk.
A probléma fel van vetve, térjünk rá a megoldására.
Ismertesse velünk az irányító műveletet (), aminek köszönhetően a gép repül (a pilóta elmondta, melyik karokat húzza meg 😉). Ekkor a k-adik lépésben a koordináta ismeretében megkaphatjuk a (k + 1) lépésben az értéket:
Úgy tűnik, ez az, amire szüksége van! És itt nincs szükség Kálmán-szűrőre. De nem minden ilyen egyszerű .. A valóságban nem tudunk minden, a repülést befolyásoló külső tényezőt figyelembe venni, ezért a képlet a következő formát ölti:
hol van a külső hatások, a motor tökéletlensége stb.
Szóval mi történik? A (k + 1) lépésnél egyrészt pontatlan az érzékelő leolvasása, másrészt az előző lépésben kapott értékből kapott pontatlanul számított érték.
A Kalman-szűrő ötlete az, hogy a kívánt koordináta pontos becslését (esetünkben) két pontatlan értékből (különböző súlyegyütthatókkal véve) kapja meg. Általában a mért érték bármilyen lehet (hőmérséklet, sebesség...). Íme, mi történik:
Matematikai számításokkal minden lépésben megkaphatunk egy képletet a Kálmán-együttható kiszámításához, de ahogyan a cikk elején megállapodtunk, nem fogunk belemenni a számításokba, különösen mivel a gyakorlatban bebizonyosodott, hogy a Kálmán-együttható mindig k növekedésével egy bizonyos értékre hajlik. Megkapjuk képletünk első egyszerűsítését:
Most tegyük fel, hogy nincs kommunikáció a pilótával, és nem ismerjük a vezérlési műveletet. Úgy tűnik, hogy ebben az esetben nem használhatjuk a Kálmán szűrőt, de ez nem így van 😉 Egyszerűen „kidobjuk” a képletből, amit nem tudunk, akkor
A legegyszerűbb Kálmán képletet kapjuk, amely ennek ellenére az ilyen „kemény” egyszerűsítések ellenére tökéletesen megbirkózik a feladatával. Ha grafikusan ábrázolja az eredményeket, valami ilyesmit kap:

Ha az érzékelőnk nagyon pontos, akkor természetesen a K súlyozási tényezőnek közel kell lennie egyhez. Ha fordított a helyzet, vagyis nem túl jó a szenzorunk, akkor K legyen közelebb a nullához.
Valószínűleg ennyi, így találtuk ki a Kálmán-szűrő algoritmust! Remélem hasznos és érthető volt a cikk =)
 Információs és kommunikációs technológiák a zeneoktatásban
Információs és kommunikációs technológiák a zeneoktatásban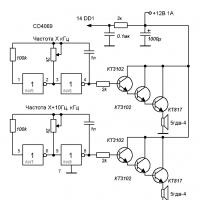 Yagma Medical Physics nagyhullámú impedanciájú eszközök
Yagma Medical Physics nagyhullámú impedanciájú eszközök Az információs kompetencia kialakulásának jellemzői Iskolások információs kompetenciájának kialakulása
Az információs kompetencia kialakulásának jellemzői Iskolások információs kompetenciájának kialakulása USB programozó (AVR): leírás, cél
USB programozó (AVR): leírás, cél Hp pavilion dv7 elemzés. Számítógépes erőforrás U SM
Hp pavilion dv7 elemzés. Számítógépes erőforrás U SM Hogyan telepíthetek DLL fájlokat Windows rendszeren?
Hogyan telepíthetek DLL fájlokat Windows rendszeren? Tűzfal letiltása A tűzfal zavarja a letiltás lejátszását
Tűzfal letiltása A tűzfal zavarja a letiltás lejátszását