على الإنترنت ، بما في ذلك على Habré ، يمكنك العثور على الكثير من المعلومات حول مرشح Kalman. لكن من الصعب العثور على اشتقاق سهل الهضم للصيغ نفسها. بدون استنتاج ، يُنظر إلى كل هذا العلم على أنه نوع من الشامانية ، وتبدو الصيغ كمجموعة من الرموز مجهولة الهوية ، والأهم من ذلك ، أن العديد من العبارات البسيطة التي تكمن على سطح نظرية لا يمكن فهمها. سيكون الغرض من هذه المقالة هو التحدث عن هذا المرشح بلغة يمكن الوصول إليها قدر الإمكان.
مرشح كالمان هو أداة قوية لتصفية البيانات. مبدأها الرئيسي هو أنه عند التصفية ، يتم استخدام المعلومات حول فيزياء الظاهرة نفسها. على سبيل المثال ، إذا كنت تقوم بتصفية البيانات من عداد السرعة للسيارة ، فإن القصور الذاتي للسيارة يمنحك الحق في إدراك القفزات السريعة جدًا في السرعة كخطأ في القياس. مرشح كالمان مثير للاهتمام لأنه ، بمعنى ما ، هو أفضل مرشح. سنناقش بمزيد من التفصيل أدناه ما تعنيه عبارة "الأفضل" بالضبط. في نهاية المقال ، سأوضح أنه في كثير من الحالات يمكن تبسيط الصيغ لدرجة أنه لن يتبقى منها شيء تقريبًا.

برنامج تعليمي

قبل التعرف على مرشح كالمان ، أقترح تذكر بعض التعريفات والحقائق البسيطة من نظرية الاحتمال.

قيمة عشوائية

عندما يقولون أنه تم إعطاء متغير عشوائي ، فإنهم يعنون أن هذه الكمية يمكن أن تأخذ قيمًا عشوائية. يأخذ قيما مختلفة مع احتمالات مختلفة. عندما تتدحرج ، على سبيل المثال ، نرد ، ستسقط مجموعة منفصلة من القيم: عندما يتعلق الأمر ، على سبيل المثال ، بسرعة الجسيم المتجول ، فمن الواضح أنه يتعين على المرء أن يتعامل مع مجموعة مستمرة من القيم. سوف نشير إلى القيم "المسقطة" لمتغير عشوائي من خلال ، ولكن في بعض الأحيان ، سنستخدم نفس الحرف ، والذي نستخدمه للدلالة على متغير عشوائي :.
في حالة وجود مجموعة مستمرة من القيم ، يتميز المتغير العشوائي بكثافة الاحتمال ، والتي تملي علينا أن احتمال "سقوط" المتغير العشوائي في منطقة مجاورة صغيرة لنقطة ذات طول يساوي. كما نرى من الصورة ، فإن هذا الاحتمال يساوي مساحة المستطيل المظلل أسفل الرسم البياني:

في كثير من الأحيان في الحياة ، تكون المتغيرات العشوائية هي Gaussian عندما تكون كثافة الاحتمال متساوية.

نرى أن الوظيفة لها شكل جرس متمركز عند نقطة وبعرض مميز للترتيب.
نظرًا لأننا نتحدث عن التوزيع الغاوسي ، فسيكون من الخطيئة عدم ذكر مصدرها. كما أن الأرقام ثابتة في الرياضيات وتحدث في أكثر الأماكن غير المتوقعة ، كذلك فإن التوزيع الغاوسي أخذ جذورًا عميقة في نظرية الاحتمال. أحد العبارات الرائعة التي تفسر جزئيًا الوجود الغاوسي هو ما يلي:
يجب أن يكون هناك متغير عشوائي بتوزيع عشوائي (في الواقع ، هناك بعض القيود على هذا التعسف ، لكنها ليست صارمة على الإطلاق). دعونا نجري التجارب ونحسب مجموع القيم "المسقطة" للمتغير العشوائي. لنقم بالكثير من هذه التجارب. من الواضح أنه في كل مرة نتلقى قيمة مختلفة للمبلغ. بمعنى آخر ، هذا المجموع هو في حد ذاته متغير عشوائي بقانون توزيع خاص به. اتضح أن قانون التوزيع لهذا المجموع يميل إلى التوزيع الغاوسي (بالمناسبة ، العرض المميز لـ "الجرس" ينمو مثل). اقرأ المزيد في ويكيبيديا: نظرية الحدود المركزية. في الحياة ، غالبًا ما توجد كميات تتكون من عدد كبير من المتغيرات العشوائية المستقلة الموزعة بالتساوي ، وبالتالي يتم توزيعها وفقًا لـ Gaussian.

يقصد

متوسط ​​قيمة المتغير العشوائي هو ما نحصل عليه في الحد إذا أجرينا الكثير من التجارب وحساب المتوسط ​​الحسابي للقيم المسقطة. يُشار إلى المتوسط ​​بطرق مختلفة: يحب علماء الرياضيات الإشارة إلى (توقع) ، وعلماء رياضيات أجانب بواسطة (التوقع). الفيزيائيون من خلال أو. سنعين بطريقة أجنبية:.
على سبيل المثال ، بالنسبة لتوزيع Gaussian ، المتوسط ​​هو.

تشتت

في حالة التوزيع الغوسي ، نرى بوضوح أن المتغير العشوائي يفضل السقوط بالقرب من قيمته المتوسطة. كما يتضح من الرسم البياني ، مبعثر مميز لقيم الترتيب. كيف يمكننا تقدير انتشار القيم لمتغير عشوائي عشوائي إذا عرفنا توزيعه. يمكنك رسم رسم بياني لكثافة احتماله وتقدير عرض الخاصية بالعين. لكننا نفضل السير على طول الطريق الجبري. يمكنك إيجاد متوسط ​​طول الانحراف (المعامل) عن المتوسط ​​:. ستكون هذه القيمة تقديرًا جيدًا للتشتت المميز للقيم. لكننا نعلم جيدًا أن استخدام الوحدات في الصيغ هو أحد الصداع ، لذلك نادرًا ما تُستخدم هذه الصيغة لتقدير الانتشار المميز.
أسهل طريقة (بسيطة من حيث الحسابات) هي العثور على. هذه القيمة تسمى التباين ، وغالبًا ما يشار إليها باسم. يسمى جذر التباين الانحراف المعياري. الانحراف المعياري هو تقدير جيد لانتشار متغير عشوائي.
على سبيل المثال ، بالنسبة لتوزيع Gaussian ، يمكننا حساب أن التباين المحدد أعلاه متساوٍ تمامًا ، مما يعني أن الانحراف المعياري متساوٍ ، وهو ما يتوافق جيدًا مع حدسنا الهندسي.
في الواقع ، هناك عملية احتيال صغيرة مخبأة هنا. الحقيقة هي أنه في تعريف التوزيع الغاوسي ، تحت الأس هو التعبير. هذان في المقام هو بالضبط بحيث يكون الانحراف المعياري مساويًا للمعامل. وهذا يعني أن صيغة التوزيع الجاوسي نفسها مكتوبة في شكل شحذ بشكل خاص حتى نأخذ في الاعتبار انحرافها المعياري.

المتغيرات العشوائية المستقلة

المتغيرات العشوائية تعتمد وليس. تخيل أنك ترمي إبرة على مستو وتكتب إحداثيات كلا الطرفين. يعتمد هذان الإحداثيان على علاقة ، ويرتبطان بشرط أن المسافة بينهما تساوي دائمًا طول الإبرة ، على الرغم من أنها قيم عشوائية.
تكون المتغيرات العشوائية مستقلة إذا كانت نتيجة أولها مستقلة تمامًا عن نتيجة الثانية منها. إذا كانت المتغيرات العشوائية مستقلة ، فإن متوسط ​​قيمة منتجها يساوي منتج متوسط ​​قيمها:

دليل

على سبيل المثال ، وجود عيون زرقاء والتخرج من المدرسة الثانوية بميدالية ذهبية هي متغيرات عشوائية مستقلة. إذا كان أصحاب العيون الزرقاء ، على سبيل المثال ، أصحاب الميداليات الذهبية ، ثم أصحاب الميداليات ذات العيون الزرقاء ، يخبرنا هذا المثال أنه إذا تم إعطاء المتغيرات العشوائية من خلال كثافاتهم الاحتمالية ، فسيتم التعبير عن استقلالية هذه القيم في حقيقة أن كثافة الاحتمال ( تم إسقاط القيمة الأولى ، والثانية) من خلال الصيغة:

ويترتب على ذلك على الفور ما يلي:

كما ترى ، يتم إجراء الإثبات للمتغيرات العشوائية التي لها طيف مستمر من القيم ويتم الحصول عليها من خلال كثافة الاحتمالات. في حالات أخرى ، تكون فكرة الإثبات متشابهة.

مرشح كالمان

صياغة المشكلة

دعنا نشير بالقيمة التي سنقيسها ، ثم نقوم بالتصفية. يمكن أن يكون هذا التنسيق ، والسرعة ، والتسارع ، والرطوبة ، والرائحة الكريهة ، ودرجة الحرارة ، والضغط ، وما إلى ذلك.
لنبدأ بمثال بسيط يقودنا إلى صياغة مشكلة عامة. تخيل أن لدينا سيارة يتم التحكم فيها عن طريق الراديو يمكنها فقط الذهاب ذهابًا وإيابًا. بمعرفة وزن السيارة وشكلها وسطح الطريق وما إلى ذلك ، قمنا بحساب كيفية تأثير عصا التحكم على سرعة الحركة.

ثم سيتغير تنسيق السيارة وفقًا للقانون:

في الحياة الواقعية ، لا يمكننا أن نأخذ في الاعتبار في حساباتنا الاضطرابات الصغيرة التي تؤثر على السيارة (الرياح ، المطبات ، الحصى على الطريق) ، وبالتالي فإن السرعة الحقيقية للسيارة ستختلف عن السرعة المحسوبة. يضاف متغير عشوائي إلى الجانب الأيمن من المعادلة المكتوبة:

لدينا مستشعر GPS مثبت على آلة كاتبة ، والذي يحاول قياس الإحداثيات الحقيقية للسيارة ، وبالطبع لا يمكنه قياسه بالضبط ، ولكنه يقيسه بخطأ ، وهو أيضًا متغير عشوائي. نتيجة لذلك ، نتلقى بيانات خاطئة من المستشعر:

وتتمثل المهمة في أنه بمعرفة قراءات المستشعر الخاطئة ، يمكنك العثور على تقدير تقريبي جيد للإحداثيات الحقيقية للسيارة.
في صياغة المهمة العامة ، يمكن أن يكون أي شيء مسؤولاً عن الإحداثيات (درجة الحرارة ، الرطوبة ...) ، وسيتم الإشارة إلى المصطلح المسؤول عن التحكم في النظام من الخارج بواسطة (في المثال باستخدام آلة). ستبدو معادلات قراءات الإحداثيات والمستشعرات كما يلي:

دعونا نناقش بالتفصيل ما نعرفه:

من الجدير بالذكر أن مهمة التصفية ليست مهمة تنعيم. نحن لا نحاول تلطيف البيانات من المستشعر ، نحن نحاول الحصول على أقرب قيمة للإحداثيات الحقيقية.

خوارزمية كالمان

سوف نجادل عن طريق الاستقراء. تخيل أنه في الخطوة الثالثة وجدنا بالفعل القيمة التي تمت تصفيتها من المستشعر ، والتي تقترب جيدًا من الإحداثيات الحقيقية للنظام. لا تنس أننا نعرف المعادلة التي تتحكم في التغيير في الإحداثي المجهول:

لذلك ، لم نتلق القيمة من المستشعر بعد ، يمكننا أن نفترض أنه في خطوة ما يتطور النظام وفقًا لهذا القانون وسيظهر المستشعر شيئًا قريبًا منه. لسوء الحظ ، لا يمكننا قول أي شيء أكثر دقة حتى الآن. من ناحية أخرى ، في خطوة ، سيكون لدينا قراءة مستشعر غير دقيقة على أيدينا.
فكرة كالمان على النحو التالي. للحصول على أفضل تقريب للإحداثيات الحقيقية ، يجب أن نختار الأرضية الوسطى بين قراءة مستشعر غير دقيق وتنبؤنا بما توقعناه منه. سنعطي وزنًا لقراءة المستشعر وسيظل الوزن على القيمة المتوقعة:

المعامل يسمى معامل كالمان. يعتمد ذلك على خطوة التكرار ، لذلك سيكون من الأصح كتابتها ، ولكن في الوقت الحالي ، حتى لا نشوش معادلات الحساب ، سنحذف فهرسها.
يجب أن نختار معامل كالمان بحيث تكون قيمة الإحداثيات المثلى الناتجة أقرب إلى القيمة الحقيقية. على سبيل المثال ، إذا علمنا أن جهاز الاستشعار الخاص بنا دقيق للغاية ، فسنثق في قراءته أكثر ونعطي القيمة وزنًا أكبر (قريب من واحد). إذا كان المستشعر ، على العكس من ذلك ، غير دقيق تمامًا ، فسنركز أكثر على القيمة المتوقعة من الناحية النظرية.
بشكل عام ، للعثور على القيمة الدقيقة لمعامل كالمان ، ما عليك سوى تقليل الخطأ:

نستخدم المعادلات (1) (تلك الموجودة في المربع بخلفية زرقاء) لإعادة كتابة التعبير عن الخطأ:

دليل

حان الوقت الآن لمناقشة ماذا يعني التعبير تقليل الخطأ؟ بعد كل شيء ، الخطأ ، كما نرى ، هو في حد ذاته متغير عشوائي ويأخذ في كل مرة قيمًا مختلفة. في الواقع ، لا يوجد نهج واحد يناسب الجميع لتحديد ما يعنيه أن الخطأ ضئيل. تمامًا كما في حالة تباين متغير عشوائي ، عندما حاولنا تقدير العرض المميز لانتشاره ، لذلك سنختار هنا أبسط معيار للحسابات. سنقلل من متوسط ​​الخطأ التربيعي:

دعنا نكتب التعبير الأخير:

دليل

من حقيقة أن جميع المتغيرات العشوائية المضمنة في التعبير عن مستقلة ، يترتب على ذلك أن جميع المصطلحات "المتقاطعة" تساوي صفرًا:

استخدمنا حقيقة أن صيغة التباين تبدو أبسط بكثير:

يأخذ هذا التعبير قيمة دنيا عندما (نساوي المشتق بالصفر):

هنا نكتب بالفعل تعبيرًا لمعامل كالمان مع مؤشر الخطوة ، وبالتالي نؤكد أنه يعتمد على خطوة التكرار.
نعوض بالقيمة المثلى التي تم الحصول عليها في التعبير الذي قمنا بتصغيره. استلمنا؛

لقد تم إنجاز مهمتنا. حصلنا على صيغة تكرارية لحساب معامل كالمان.
دعونا نلخص المعرفة المكتسبة في إطار واحد:

مثال

كود ماتلاب

امسح الكل؛ N = 100٪ عدد العينات a = 0.1٪ تسارع sigmaPsi = 1 sigmaEta = 50 ؛ ك = 1: N x = k x (1) = 0 z (1) = x (1) + normrnd (0، sigmaEta) ؛ بالنسبة إلى t = 1: (N-1) x (t + 1) = x (t) + a * t + normrnd (0، sigmaPsi) ؛ ض (تي + 1) = س (تي + 1) + نوررند (0 ، سيجما إيتا) ؛ نهاية؛ ٪ kalman filter xOpt (1) = z (1) ؛ eOpt (1) = sigmaEta ؛ بالنسبة إلى t = 1: (N-1) eOpt (t + 1) = sqrt ((sigmaEta ^ 2) * (eOpt (t) ^ 2 + sigmaPsi ^ 2) / (sigmaEta ^ 2 + eOpt (t) ^ 2 + sigmaPsi ^ 2)) K (t + 1) = (eOpt (t + 1)) ^ 2 / sigmaEta ^ 2 xOpt (t + 1) = (xOpt (t) + a * t) * (1-K (t +1)) + K (t + 1) * z (t + 1) end ؛ مؤامرة (ك ، xOpt ، ك ، ض ، ك ، س)

التحليلات

إذا تتبعنا كيف يتغير معامل كالمان بخطوة التكرار ، فيمكن إثبات أنه يستقر دائمًا عند قيمة معينة. على سبيل المثال ، عندما ترتبط أخطاء جذر متوسط ​​التربيع في المستشعر والنموذج ببعضهما البعض بعشرة إلى واحد ، فإن مخطط معامل كالمان اعتمادًا على خطوة التكرار يبدو كما يلي:

في المثال التالي ، سنناقش كيف يمكن لهذا أن يجعل حياتنا أسهل بكثير.

المثال الثاني

من الناحية العملية ، غالبًا ما يحدث أننا لا نعرف شيئًا على الإطلاق عن النموذج المادي لما نقوم بترشيحه. على سبيل المثال ، تريد تصفية القراءات من مقياس التسارع المفضل لديك. أنت لا تعرف مسبقًا أي قانون تنوي تشغيل مقياس التسارع. معظم المعلومات التي يمكنك الحصول عليها هي تباين خطأ المستشعر. في مثل هذا الموقف الصعب ، يمكن دفع كل جهل بنموذج الحركة إلى متغير عشوائي:

لكن ، بصراحة ، مثل هذا النظام لا يلبي مطلقًا الشروط التي فرضناها على المتغير العشوائي ، لأنه الآن جميع فيزياء الحركة غير المعروفة لنا مخفية هناك ، وبالتالي لا يمكننا القول أنه في أوقات مختلفة من النموذج الأخطاء مستقلة عن بعضها البعض وأن قيمها المتوسطة تساوي صفرًا. في هذه الحالة ، بشكل عام ، لا تنطبق نظرية مرشح كالمان. لكننا لن ننتبه إلى هذه الحقيقة ، ولكن ، بغباء ، نطبق كل الصيغ العملاقة ، ونختار المعاملات بالعين ، بحيث تبدو البيانات التي تمت تصفيتها جذابة.
لكن يمكنك أن تأخذ مسارًا مختلفًا أبسط بكثير. كما رأينا أعلاه ، فإن معامل كالمان يستقر دائمًا نحو قيمة مع زيادة. لذلك ، بدلاً من اختيار المعاملات وإيجاد معامل كالمان باستخدام الصيغ المعقدة ، يمكننا اعتبار هذا المعامل ثابتًا دائمًا ، واختيار هذا الثابت فقط. هذا الافتراض لا يفسد شيئًا تقريبًا. أولاً ، نحن بالفعل نستخدم نظرية كالمان بشكل غير قانوني ، وثانيًا ، يستقر معامل كالمان بسرعة إلى ثابت. نتيجة لذلك ، سيكون كل شيء مبسطًا للغاية. بشكل عام ، لا نحتاج إلى أي معادلات من نظرية كالمان ، نحتاج فقط إلى إيجاد قيمة مقبولة وإدخالها في الصيغة التكرارية:

يوضح الرسم البياني التالي بيانات من مستشعر خيالي تمت تصفيته بطريقتين مختلفتين. بشرط ألا نعلم شيئاً عن فيزياء الظاهرة. الطريقة الأولى صادقة ، مع كل الصيغ من نظرية كالمان. والثاني مبسط بدون صيغ.

كما نرى ، الأساليب متشابهة تقريبًا. لوحظ اختلاف بسيط فقط في البداية ، عندما لم يستقر معامل كالمان بعد.

مناقشة

كما رأينا ، فإن الفكرة الرئيسية لمرشح كالمان هي إيجاد معامل مثل القيمة المصفاة

في المتوسط ​​، سيكون أقل اختلاف عن القيمة الحقيقية للإحداثي. يمكننا أن نرى أن القيمة المصفاة هي دالة خطية لقراءة المستشعر والقيمة المصفاة السابقة. والقيمة المصفاة السابقة هي بدورها دالة خطية لقراءة المستشعر وقيمة التصفية السابقة. وهكذا ، حتى تتكشف السلسلة بالكامل. وهذا يعني أن القيمة المصفاة تعتمد على للجميعقراءات المستشعر السابقة خطيًا:

لذلك ، يسمى مرشح كالمان مرشح خطي.
يمكن إثبات أن مرشح كالمان هو الأفضل بين جميع المرشحات الخطية. الأفضل بمعنى أن المربع المتوسط ​​لخطأ المرشح ضئيل.

حالة متعددة الأبعاد

يمكن تعميم النظرية الكاملة لمرشح كالمان على الحالة متعددة الأبعاد. تبدو الصيغ هناك مخيفة أكثر قليلاً ، لكن فكرة اشتقاقها هي نفسها كما في الحالة أحادية البعد. يمكنك رؤيتهم في هذا المقال الممتاز: http://habrahabr.ru/post/140274/.
وفي هذا رائع فيديويتم تحليل مثال على كيفية استخدامها.

تعتبر مرشحات Wiener هي الأنسب لمعالجة العمليات أو أقسام العمليات بشكل عام (معالجة الكتل). للمعالجة المتسلسلة ، يلزم تقدير حالي للإشارة في كل دورة ساعة ، مع مراعاة المعلومات التي تدخل إدخال المرشح أثناء عملية المراقبة.

مع تصفية Wiener ، ستتطلب كل عينة إشارة جديدة إعادة حساب جميع أوزان المرشح. في الوقت الحالي ، أصبحت المرشحات التكيفية منتشرة على نطاق واسع ، حيث يتم استخدام المعلومات الجديدة الواردة لتصحيح تقييم الإشارة الذي تم إجراؤه مسبقًا باستمرار (تتبع الهدف في الرادار ، وأنظمة التحكم الآلي في التحكم ، وما إلى ذلك). تعتبر المرشحات التكيفية من النوع التكراري المعروف باسم مرشح كالمان ذات أهمية خاصة.

تستخدم هذه المرشحات على نطاق واسع في حلقات التحكم في أنظمة التنظيم والتحكم الأوتوماتيكية. ومن هناك ظهروا ، كما يتضح من مثل هذه المصطلحات المحددة المستخدمة لوصف عملهم على أنه فضاء الدولة.

تتمثل إحدى المهام الرئيسية التي يتعين حلها في ممارسة الحوسبة العصبية في الحصول على خوارزميات سريعة وموثوقة لتعلم الشبكات العصبية. في هذا الصدد ، قد يكون من المفيد استخدام المرشحات الخطية في حلقة التغذية الراجعة. نظرًا لأن خوارزميات التدريب تكرارية بطبيعتها ، يجب أن يكون هذا المرشح مقدرًا تعاوديًا متسلسلًا.

مشكلة تقدير المعلمة

من مشاكل نظرية القرارات الإحصائية ، والتي لها أهمية عملية كبيرة ، مشكلة تقدير متجهات الحالة ومعلمات الأنظمة ، والتي تمت صياغتها على النحو التالي. افترض أنه من الضروري تقدير قيمة معامل المتجه $ X $ ، والذي لا يمكن الوصول إليه للقياس المباشر. بدلاً من ذلك ، يتم قياس معامل آخر $ Z $ ، اعتمادًا على $ X $. مشكلة التقدير هي الإجابة على السؤال: ماذا يمكن أن يقال عن $ X $ ، بمعرفة $ Z $. في الحالة العامة ، يعتمد إجراء التقييم الأمثل للمتجه $ X $ على المعيار المقبول لجودة التقييم.

على سبيل المثال ، يتطلب النهج البايزي لمشكلة تقدير المعلمة استكمال معلومات مسبقة حول الخصائص الاحتمالية للمعامل الذي يتم تقديره ، والذي غالبًا ما يكون مستحيلًا. في هذه الحالات ، يلجأون إلى طريقة المربعات الصغرى (OLS) ، والتي تتطلب قدرًا أقل من المعلومات المسبقة.

دعونا نفكر في تطبيق OLS للحالة عندما يكون متجه الملاحظة $ Z $ مرتبطًا بمتجه تقدير المعلمة $ X $ بواسطة نموذج خطي ، وتحتوي الملاحظة على ضوضاء $ V $ غير مرتبطة بالمعلمة المقدرة:

$ Z = HX + V $ ، (1)

حيث $ H $ مصفوفة تحويل تصف العلاقة بين الكميات المرصودة والمعلمات المقدرة.

يتم كتابة التقدير $ X $ لتقليل الخطأ التربيعي على النحو التالي:

$ X_ (оц) = (H ^ TR_V ^ (- 1) H) ^ (- 1) H ^ TR_V ^ (- 1) Z $ ، (2)

دع الضوضاء $ V $ غير مرتبطة ، في هذه الحالة المصفوفة $ R_V $ هي فقط مصفوفة الهوية ، وتصبح معادلة التقدير أبسط:

X_ دولار أمريكي (نقاط) = (H ^ TH) ^ (- 1) H ^ TZ $ ، (3)

الكتابة في شكل مصفوفة توفر الورق بشكل كبير ، ولكن قد يكون الأمر غير معتاد بالنسبة للبعض. المثال التالي ، مأخوذ من دراسة يو إم كورشونوف ، "الأسس الرياضية لعلم التحكم الآلي" ، يوضح كل هذا.
الدائرة الكهربائية التالية متاحة:

القيم المرصودة في هذه الحالة هي قراءات الأجهزة $ A_1 = 1 A ، A_2 = 2 A ، V = 20 B $.

بالإضافة إلى ذلك ، فإن المقاومة $ R = 5 $ أوم معروفة. مطلوب تقدير بأفضل طريقة ، من وجهة نظر معيار الحد الأدنى لمتوسط ​​مربع الخطأ ، قيم التيارات $ I_1 $ و $ I_2 $. أهم شيء هنا هو وجود علاقة ما بين القيم المرصودة (قراءات الأداة) والمعلمات المقدرة. وهذه المعلومات تأتي من الخارج.

في هذه الحالة ، هذه هي قوانين كيرشوف ، في حالة التصفية (التي ستتم مناقشتها بمزيد من التفصيل) - نموذج الانحدار الذاتي لسلسلة زمنية ، والتي تفترض اعتماد القيمة الحالية على القيم السابقة.

لذا ، فإن معرفة قوانين كيرشوف ، التي لا علاقة لها بنظرية القرارات الإحصائية ، تجعل من الممكن إنشاء اتصال بين القيم المرصودة والمعلمات المقدرة (من درس الهندسة الكهربائية - يمكنهم التحقق ، والباقي سيكون لديهم لأخذ كلمتهم من أجلها):

$$ z_1 = A_1 = I_1 + \ xi_1 = 1 $$

$$ z_2 = A_2 = I_1 + I_2 + \ xi_2 = 2 $$

$$ z_2 = V / R = I_1 + 2 * I_2 + \ xi_3 = 4 $$

إنه في شكل متجه:

$$ \ تبدأ (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ start (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) \ start (vmatrix) I_1 \ \ I_2 \ end (vmatrix) + \ start (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

أو $ Z = HX + V $ حيث

$$ Z = \ start (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ start (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix) ؛ H = \ start (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) ؛ X = \ start (vmatrix) I_1 \\ I_2 \ end (vmatrix) ؛ V = \ start (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

بالنظر إلى قيم التداخل غير المرتبط ببعضها البعض ، نجد تقدير I 1 و I 2 بطريقة المربعات الصغرى وفقًا للصيغة 3:

$ H ^ TH = \ start (vmatrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatrix) \ start (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) = \ start (vmatrix) 3 & 3 \\ 3 & 5 \ end (vmatrix) ؛ (H ^ TH) ^ (- 1) = \ frac (1) (6) \ start (vmatrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) $؛

$ H ^ TZ = \ start (vmatrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatrix) \ start (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix) = \ start (vmatrix) 7 \ 10 \ نهاية (مصفوفة) ؛ X (ots) = \ frac (1) (6) \ start (vmatrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) \ start (vmatrix) 7 \\ 10 \ end (vmatrix) = \ frac (1) (6) \ start (vmatrix) 5 \\ 9 \ end (vmatrix) $؛

إذن I_1 = 5/6 = 0.833 دولار أسترالي ؛ I_2 دولار أمريكي = 9/6 = 1.5 دولار أمريكي.

مهمة الترشيح

على عكس مشكلة تقدير المعلمات ، التي لها قيم ثابتة ، في مشكلة التصفية ، يلزم تقدير العمليات ، أي العثور على التقديرات الحالية لإشارة تتغير بمرور الوقت ، مشوهة بالضوضاء ، وبالتالي ، لا يمكن الوصول إليه لقياس مباشر. بشكل عام ، يعتمد نوع خوارزميات التصفية على الخصائص الإحصائية للإشارة والضوضاء.

سنفترض أن الإشارة المفيدة هي دالة متغيرة ببطء للوقت ، والتداخل هو ضوضاء غير مرتبطة. سنستخدم طريقة المربعات الصغرى ، مرة أخرى بسبب عدم وجود معلومات مسبقة حول الخصائص الاحتمالية للإشارة والتداخل.

أولاً ، نحصل على تقدير للقيمة الحالية لـ $ x_n $ بناءً على $ k $ المتاح لأحدث قيم السلسلة الزمنية $ z_n، z_ (n-1)، z_ (n-2) \ dots z_ (ن- (ك -1)) $. نموذج الملاحظة هو نفسه كما في مشكلة تقدير المعلمة:

من الواضح أن $ Z $ عبارة عن متجه عمود يتكون من القيم المرصودة للسلسلة الزمنية $ z_n، z_ (n-1)، z_ (n-2) \ dots z_ (n- (k-1)) $، $ V $ - عمود متجه للضوضاء $ \ xi _n، \ xi _ (n-1)، \ xi_ (n-2) \ dots \ xi_ (n- (k-1)) $ ، تشويه الحقيقة الإشارة. ماذا تعني الرموز $ H $ و $ X $؟ ما ، على سبيل المثال ، متجه العمود $ X $ الذي يمكن أن نتحدث عنه إذا كان كل ما هو مطلوب هو إعطاء تقدير للقيمة الحالية للسلسلة الزمنية؟ وما المقصود بمصفوفة التحويل $ H $ غير واضح على الإطلاق.

لا يمكن الإجابة على كل هذه الأسئلة إلا إذا تم تقديم مفهوم نموذج توليد الإشارة في الاعتبار. وهذا يعني أن هناك حاجة إلى نموذج ما للإشارة الأصلية. هذا أمر مفهوم ، في حالة عدم وجود معلومات مسبقة حول الخصائص الاحتمالية للإشارة والتداخل ، كل ما تبقى هو وضع افتراضات. يمكنك أن تسميها الكهانة على القهوة ، لكن الخبراء يفضلون مصطلحات مختلفة. يطلق عليه على "مجفف الشعر" نموذج حدودي.

في هذه الحالة ، يتم تقدير معلمات هذا النموذج بالذات. عند اختيار نموذج توليد إشارة مناسب ، تذكر أنه يمكن توسيع أي وظيفة تحليلية في سلسلة تايلور. من الخصائص المذهلة لسلسلة Taylor أن شكل الدالة عند أي مسافة محدودة $ t $ من نقطة ما $ x = a $ يتم تحديده بشكل فريد من خلال سلوك الوظيفة في منطقة صغيرة لا متناهية من النقطة $ x = a $ (نتحدث عن مشتقاته من الرتب الأولى والأعلى).

وبالتالي ، فإن وجود سلسلة تايلور يعني أن الوظيفة التحليلية لها هيكل داخلي مع اقتران قوي جدًا. على سبيل المثال ، إذا قصرنا أنفسنا على ثلاثة أعضاء من سلسلة Taylor ، فسيبدو نموذج توليد الإشارة كما يلي:

$ x_ (n-i) = F _ (- i) x_n $ ، (4)

$$ X_n = \ start (vmatrix) x_n \\ x "_n \\ x" "_ n \ end (vmatrix) ؛ F _ (- i) = \ start (vmatrix) 1 & -i & i ^ 2/2 \\ 0 & 1 & -i \\ 0 & 0 & 1 \ end (vmatrix) $$

أي ، الصيغة 4 ، لترتيب معين من كثير الحدود (في المثال ، 2) تنشئ اتصالاً بين قيمة $ n $ -th للإشارة في التسلسل الزمني و $ (n-i) $ -th. وبالتالي ، فإن متجه الحالة المقدرة في هذه الحالة يشمل ، بالإضافة إلى القيمة المقدرة الفعلية ، المشتقات الأولى والثانية للإشارة.

في نظرية التحكم الآلي ، يمكن أن يسمى هذا المرشح مرشح الاستاتية من الدرجة الثانية. تبدو مصفوفة التحويل $ H $ لهذه الحالة (يتم إجراء التقدير على أساس العينات الحالية و $ k-1 $ السابقة) كما يلي:

$$ H = \ start (vmatrix) 1 & -k & k ^ 2/2 \\ - & - & - \\ 1 & -2 & 2 \\ 1 & -1 & 0.5 \\ 1 & 0 & 0 \ النهاية (vmatrix) $$

يتم الحصول على كل هذه الأرقام من سلسلة تايلور بافتراض أن الفاصل الزمني بين القيم المتجاورة المرصودة ثابت ويساوي 1.

لذلك ، تم تقليل مهمة التصفية وفقًا لافتراضاتنا إلى مهمة تقدير المعلمات ؛ في هذه الحالة ، يتم تقدير معلمات نموذج توليد الإشارة المعتمد. ويتم تقدير قيم متجه الحالة $ X $ وفقًا لنفس الصيغة 3:

$$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $$

بشكل أساسي ، قمنا بتنفيذ عملية تقدير حدودي على أساس نموذج الانحدار التلقائي لعملية توليد الإشارة.

يمكن تنفيذ الصيغة 3 برمجيًا بسهولة ، لذلك تحتاج إلى ملء المصفوفة $ H $ وعمود المتجه للملاحظات $ Z $. تسمى هذه المرشحات مرشحات الذاكرة المحدودة، حيث أنهم يستخدمون ملاحظات $ k $ الأخيرة للحصول على التقدير الحالي لـ $ X_ (nоц) $. في كل دورة مراقبة جديدة ، تتم إضافة دورة جديدة إلى المجموعة الحالية من الملاحظات ويتم تجاهل القديمة. تسمى هذه العملية للحصول على الدرجات نافذة منزلقة.

تنامي فلاتر الذاكرة

تحتوي المرشحات ذات الذاكرة المحدودة على العيب الرئيسي وهو أنه بعد كل ملاحظة جديدة ، من الضروري إعادة إجراء إعادة حساب كاملة لجميع البيانات المخزنة في الذاكرة. بالإضافة إلى ذلك ، لا يمكن بدء حساب التقديرات إلا بعد تجميع نتائج الملاحظات الأولى $ k $. وهذا يعني أن هذه المرشحات لها وقت عابر طويل.

لمكافحة هذا العيب ، من الضروري التبديل من مرشح الذاكرة الدائمة إلى مرشح باستخدام الذاكرة المتنامية... في مثل هذا المرشح ، يجب أن يتطابق عدد القيم المرصودة التي يتم إجراء التقدير مع الرقم n للملاحظة الحالية. وهذا يجعل من الممكن الحصول على تقديرات تبدأ من عدد المشاهدات التي تساوي عدد مكونات المتجه المقدر $ X $. ويتم تحديد ذلك بترتيب النموذج المعتمد ، أي عدد المصطلحات المستخدمة في النموذج من سلسلة تايلور.

في نفس الوقت ، مع زيادة n ، تتحسن خصائص التنعيم للمرشح ، أي تزداد دقة التقديرات. ومع ذلك ، يرتبط التنفيذ المباشر لهذا النهج بزيادة في التكاليف الحسابية. لذلك ، يتم تنفيذ عوامل تصفية الذاكرة المتزايدة مثل متكرر.

الحقيقة هي أنه بحلول الوقت n لدينا بالفعل تقدير $ X _ ((n-1) оц) $ ، والذي يحتوي على معلومات حول جميع الملاحظات السابقة $ z_n، z_ (n-1)، z_ (n-2) \ النقاط z_ (n- (k-1)) $. يتم الحصول على التقدير $ X_ (nоц) $ من الملاحظة التالية $ z_n $ باستخدام المعلومات المخزنة في التقدير $ X _ ((n-1)) (\ mbox (оц)) $. يسمى هذا الإجراء بالترشيح المتكرر ويتكون مما يلي:

• وفقًا لتقدير $ X _ ((n-1)) (\ mbox (оц)) $ توقع تقدير $ X_n $ وفقًا للصيغة 4 مع $ i = 1 $: $ X _ (\ mbox (nоtsapriori)) = F_1X _ ((n-1) sc) $. هذا تقدير مسبق.
• وفقًا لنتائج الملاحظة الحالية $ z_n $ ، يتم تحويل هذا التقدير المسبق إلى تقدير حقيقي ، أي لاحق ؛
• يتكرر هذا الإجراء في كل خطوة ، بدءًا من $ r + 1 $ ، حيث $ r $ هو ترتيب التصفية.

تبدو الصيغة النهائية للتصفية المتكررة كما يلي:

$ X _ ((n-1) оц) = X _ (\ mbox (nоtsapriori)) + (H ^ T_nH_n) ^ (- 1) h ^ T_0 (z_n - h_0 X _ (\ mbox (nоtsapriori))) $ ، (6)

أين مرشحنا من الدرجة الثانية:

يعد مرشح الذاكرة المتنامي المستند إلى الصيغة 6 حالة خاصة لخوارزمية التصفية المعروفة باسم مرشح كالمان.

في التطبيق العملي لهذه الصيغة ، يجب أن نتذكر أن التقدير المسبق المتضمن فيها يتم تحديده بواسطة الصيغة 4 ، والقيمة $ h_0 X _ (\ mbox (notspriori)) $ هي المكون الأول للمتجه $ X _ (\ mbox (notspriori)) $.

يحتوي مرشح الذاكرة المتنامي على ميزة مهمة واحدة. إذا نظرت إلى الصيغة 6 ، فإن النتيجة النهائية هي مجموع متجه النتيجة المتوقعة ومصطلح التصحيح. هذا التصحيح كبير بالنسبة إلى $ n $ الصغير ويقل مع زيادة $ n $ ، ويميل إلى الصفر مثل $ n \ rightarrow \ infty $. أي ، مع زيادة n ، تنمو خصائص التنعيم للمرشح ويبدأ النموذج المتأصل فيه في الهيمنة. لكن الإشارة الحقيقية يمكن أن تتوافق مع النموذج فقط في مناطق معينة ، وبالتالي تتدهور دقة التنبؤ.

لمكافحة هذا ، بدءًا من بعض $ n $ ، يتم فرض حظر على مزيد من تقليل مصطلح التصحيح. هذا يعادل تغيير عرض النطاق الترددي للمرشح ، أي ، بالنسبة إلى n الصغيرة ، يكون المرشح أوسع (أقل بالقصور الذاتي) ، بالنسبة إلى n الكبيرة يصبح أكثر قصورًا.

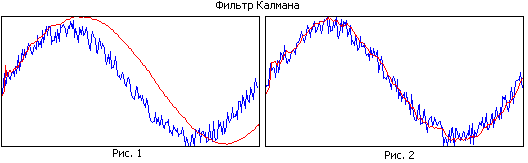
قارن الشكل 1 والشكل 2. في الشكل الأول ، يحتوي المرشح على ذاكرة كبيرة ، بينما ينعم بشكل جيد ، ولكن بسبب النطاق الضيق ، يتأخر المسار المقدر خلف الحقيقي. في الشكل الثاني ، تكون ذاكرة المرشح أصغر ، وهي سلسة بشكل أسوأ ، لكنها تتبع المسار الحقيقي بشكل أفضل.

المؤلفات

1. YM Korshunov "الأسس الرياضية لعلم التحكم الآلي"
2. بالاكريشنان AV Balakrishnan "نظرية ترشيح كالمان"
3. VNFomin "التقدير المتكرر والترشيح التكيفي"
4. سي إف إن كوين ، P.M. منح "عوامل التكييف التكيفية"

يستخدم هذا المرشح في مجالات مختلفة - من هندسة الراديو إلى الاقتصاد. سنناقش هنا الفكرة الرئيسية لهذا الفلتر ، ومعنى وجوهر هذا المرشح. سيتم تقديمه بأبسط طريقة ممكنة.
لنفترض أن لدينا حاجة لقياس بعض كميات الجسم. في الهندسة الراديوية ، غالبًا ما يتعاملون مع قياسات الفولتية عند خرج جهاز معين (جهاز استشعار ، هوائي ، إلخ). في مثال مخطط كهربية القلب (انظر) نتعامل مع قياسات القدرات الحيوية على جسم الإنسان. في علم الاقتصاد ، على سبيل المثال ، يمكن أن تكون القيمة المقاسة أسعار الصرف. كل يوم يختلف سعر الصرف ، أي كل يوم تعطينا "قياساته" قيمة مختلفة. وإذا أردنا التعميم ، فيمكننا القول إن معظم نشاط الشخص (إن لم يكن كله) يتم اختزاله بدقة إلى قياسات ومقارنات ثابتة لكميات معينة (انظر الكتاب).
لذا ، افترض أننا نقيس شيئًا ما باستمرار. لنفترض أيضًا أن قياساتنا تأتي دائمًا مع بعض الأخطاء - وهذا أمر مفهوم ، لأنه لا توجد أدوات قياس مثالية ، وكل منها ينتج نتيجة مع وجود خطأ. في أبسط الحالات ، يمكن اختزال ما تم وصفه إلى التعبير التالي: z = x + y ، حيث x هي القيمة الحقيقية التي نريد قياسها والتي يمكن قياسها إذا كان لدينا جهاز قياس مثالي ، y هو قدم خطأ القياس بواسطة جهاز القياس ، و z - القيمة التي قمنا بقياسها. لذا فإن مهمة مرشح كالمان هي التخمين (تحديد) من z المقاسة ، ولكن ما هي القيمة الحقيقية لـ x عندما تلقينا z (حيث القيمة الحقيقية وخطأ القياس "تجلس"). من الضروري تصفية (استبعاد) القيمة الحقيقية لـ x من z - إزالة الضوضاء المشوهة y من z. بمعنى ، وجود المبلغ المتاح فقط ، نحتاج إلى تخمين الشروط التي أعطت هذا المبلغ.
في ضوء ما سبق ، سنقوم الآن بصياغة كل شيء على النحو التالي. افترض أن هناك رقمين عشوائيين فقط. نحن نعطي مجموعهم فقط ومطلوب منا أن نحدد من خلال هذا المجموع ما هي الشروط. على سبيل المثال ، لدينا الرقم 12 ويقولون: 12 هو مجموع العددين x و y ، والسؤال هو ما يساوي x و y. للإجابة على هذا السؤال ، نكوّن المعادلة: x + y = 12. حصلنا على معادلة واحدة ذات مجهولين ، لذلك ، بالمعنى الدقيق للكلمة ، لا يمكن إيجاد عددين يعطيان هذا المجموع. لكن لا يزال بإمكاننا قول شيء عن هذه الأرقام. يمكننا القول أنه كان إما 1 و 11 ، أو 2 و 10 ، أو 3 و 9 ، أو 4 و 8 ، وما إلى ذلك ، كما أنه إما 13 و -1 ، أو 14 و -2 ، أو 15 و- 3 ، إلخ. أي بالمجموع (في مثالنا ، 12) ، يمكننا تحديد مجموعة الخيارات الممكنة التي تضيف ما يصل بالضبط إلى 12. أحد هذه الخيارات هو الزوج الذي نبحث عنه ، والذي أعطى بالفعل 12 الآن. تجدر الإشارة أيضًا إلى أن جميع متغيرات أزواج الأعداد التي تعطي إجماليًا 12 تشكل خطًا مستقيمًا كما هو موضح في الشكل 1 ، والذي يتم تقديمه بواسطة المعادلة x + y = 12 (y = -x + 12).

رسم بياني 1

وبالتالي ، فإن الزوج الذي نبحث عنه يقع في مكان ما على هذا الخط المستقيم. أكرر ، من المستحيل الاختيار من بين كل هذه الخيارات الزوج الذي كان في الواقع - الذي أعطى الرقم 12 ، دون أي أدلة إضافية. لكن، في الحالة التي تم فيها اختراع مرشح كالمان ، هناك مثل هذه التلميحات... شيء معروف عن الأرقام العشوائية مقدمًا. على وجه الخصوص ، يُعرف هناك ما يسمى الرسم البياني للتوزيع لكل زوج من الأرقام. عادة ما يتم الحصول عليها بعد ملاحظة طويلة إلى حد ما لحدوث هذه الأرقام العشوائية للغاية. أي ، على سبيل المثال ، من المعروف من التجربة أنه في 5٪ من الحالات ، يسقط الزوج x = 1 ، y = 8 عادةً (نشير إلى هذا الزوج على النحو التالي: (1،8)) ، في 2٪ من الحالات زوج س = 2 ، ص = 3 (2،3) ، في 1٪ من الحالات زوج (3.1) ، في 0.024٪ من الحالات زوج (11.1) ، إلخ. مرة أخرى ، تم تعيين هذا الرسم البياني لجميع الأزواجالأرقام ، بما في ذلك تلك التي تشكل ما مجموعه 12. وهكذا ، لكل زوج ، والذي يعطي إجمالي 12 ، يمكننا القول ، على سبيل المثال ، أن الزوج (1 ، 11) يقع في 0.8٪ من الحالات ، زوج ( 2 ، 10) - في 1٪ من الحالات ، زوج (3 ، 9) - في 1.5٪ من الحالات ، إلخ. وبالتالي ، يمكننا استخدام المدرج التكراري لتحديد النسبة المئوية للحالات التي يكون مجموع شروط الزوج فيها 12. افترض ، على سبيل المثال ، في 30٪ من الحالات أن المجموع هو 12. وفي الـ 70٪ المتبقية تقع الأزواج المتبقية خارج - هؤلاء هم (1،8) ، (2 ، 3) ، (3،1) ، إلخ. - تلك التي تضيف ما يصل إلى أرقام بخلاف 12. ودعنا ، على سبيل المثال ، زوج (7.5) يسقط في 27٪ من الحالات ، في حين أن جميع الأزواج الأخرى التي تضيف ما يصل إلى 12 تسقط في 0.024٪ + 0.8٪ + 1٪ + 1.5٪ +… = 3٪ من الحالات. لذلك ، وفقًا للرسم البياني ، اكتشفنا أن الأرقام التي تعطي إجماليًا 12 تسقط في 30٪ من الحالات. في الوقت نفسه ، نعلم أنه إذا سقط 12 ، فغالبًا (27٪ من 30٪) يكون السبب في ذلك هو الزوج (7.5). هذا هو ، إذا بالفعلمع طرح 12 مرة ، يمكننا القول أنه في 90٪ (27٪ من 30٪ - أو ، وهو نفس العدد 27 مرة من كل 30) ، فإن سبب طرد 12 هو زوج (7.5). مع العلم أن السبب في أغلب الأحيان للحصول على مجموع يساوي 12 هو الزوج (7.5) ، فمن المنطقي أن نفترض أنه على الأرجح سقط الآن. بالطبع ، لا تزال حقيقة أنه في الواقع الآن يتكون الرقم 12 من هذا الزوج المعين ، ومع ذلك ، في المرات القادمة ، إذا صادفنا 12 ، ونفترض مرة أخرى الزوج (7.5) ، ثم في مكان ما في 90٪ من الحالات من 100٪ سنكون على حق. لكن إذا افترضنا الزوج (2 ، 10) ، فسنكون على حق فقط 1٪ من 30٪ من الوقت ، وهو 3.33٪ تخمينات صحيحة مقارنة بـ 90٪ إذا افترضنا الزوج (7.5). هذا كل شيء - هذا هو الهدف من خوارزمية مرشح كالمان. أي أن مرشح كالمان لا يضمن أنه لن يخطئ في تحديد الاستدعاء ، لكنه يضمن أنه سيرتكب خطأ الحد الأدنى لعدد المرات (سيكون احتمال الخطأ ضئيلًا) ، لأنه يستخدم الإحصائيات - رسم بياني لأزواج الأرقام المفقودة. يجب التأكيد أيضًا على أن ما يسمى بكثافة التوزيع الاحتمالي (PDF) غالبًا ما تستخدم في خوارزمية ترشيح كالمان. ومع ذلك ، يجب أن تفهم أن المعنى هو نفس المعنى الموجود في المدرج التكراري. علاوة على ذلك ، الرسم البياني هو وظيفة مبنية على أساس PDF وهو تقريبها (انظر ، على سبيل المثال ،).
من حيث المبدأ ، يمكننا تمثيل هذا الرسم البياني كدالة لمتغيرين - أي كسطح فوق المستوى xy. عندما يكون السطح أعلى ، هناك احتمال أكبر للزوج المقابل. يوضح الشكل 2 مثل هذا السطح.

الصورة 2

كما ترون أعلاه ، الخط المستقيم x + y = 12 (الذي يحتوي على خيارات للأزواج بإجمالي 12) ، توجد نقاط السطح على ارتفاعات مختلفة وأعلى ارتفاع للخيار الذي يحتوي على إحداثيات (7،5). وعندما نواجه مبلغًا يساوي 12 ، في 90٪ من الحالات ، يكون سبب ظهور هذا المجموع هو بالضبط الزوج (7.5). أولئك. هذا الزوج ، بإجمالي 12 ، هو الذي لديه أعلى احتمال لحدوثه ، بشرط أن يكون الإجمالي 12.
وهكذا ، فإن الفكرة وراء مرشح كالمان موصوفة هنا. تم بناء جميع أنواع تعديلاته عليه - خطوة واحدة ، متكررة متعددة الخطوات ، إلخ. من أجل دراسة أعمق لمرشح كالمان ، أوصي بالكتاب: Van Tries G. Theory of Detection، Estimation and Modulation.

ملاحظة.بالنسبة لأولئك المهتمين بشرح مفاهيم الرياضيات ، ما يسمى ب "على الأصابع" ، يمكنك تقديم المشورة لهذا الكتاب ، وعلى وجه الخصوص ، فصول من قسمه "الرياضيات" (يمكنك شراء الكتاب نفسه أو فصول فردية من هو - هي).

تعد Random Forest واحدة من خوارزميات التنقيب عن البيانات المفضلة لدي. أولاً ، إنه متعدد الاستخدامات بشكل لا يصدق ؛ يمكن استخدامه لحل مشاكل الانحدار والتصنيف. ابحث عن الحالات الشاذة وحدد المتنبئين. ثانيًا ، هذه خوارزمية يصعب حقًا تطبيقها بشكل غير صحيح. ببساطة لأنه ، على عكس الخوارزميات الأخرى ، يحتوي على عدد قليل من المعلمات القابلة للتكوين. إنها أيضًا بسيطة بشكل مدهش في جوهرها. وفي الوقت نفسه ، فهي رائعة لدقتها.

ما هي الفكرة من وراء هذه الخوارزمية الرائعة؟ الفكرة بسيطة: لنفترض أن لدينا خوارزمية ضعيفة للغاية ، على سبيل المثال. إذا صنعنا الكثير من النماذج المختلفة باستخدام هذه الخوارزمية الضعيفة وقمنا بعمل متوسط ​​لنتائج تنبؤاتهم ، فإن النتيجة النهائية ستكون أفضل بكثير. هذا هو ما يسمى تدريب الفرقة في العمل. لذلك تسمى خوارزمية Random Forest "Random Forest" ، لأن البيانات التي تم الحصول عليها تخلق العديد من أشجار القرار ثم تقوم بعد ذلك بحساب متوسط ​​نتيجة تنبؤاتها. النقطة المهمة هنا هي عنصر العشوائية في تكوين كل شجرة. بعد كل شيء ، من الواضح أنه إذا أنشأنا العديد من الأشجار المتشابهة ، فإن نتيجة حساب المتوسط ​​سيكون لها دقة شجرة واحدة.

كيف يعمل؟ افترض أن لدينا بعض بيانات الإدخال. يتوافق كل عمود مع بعض المعلمات ، وكل صف يتوافق مع بعض عناصر البيانات.

يمكننا تحديد عدد معين من الأعمدة والصفوف بشكل عشوائي من مجموعة البيانات بأكملها وبناء شجرة قرار بناءً عليها.

الخميس 10 مايو 2012

الخميس 12 يناير 2012

هذا كل شئ. انتهت الرحلة التي استغرقت 17 ساعة ، وتركت روسيا في الخارج. ومن خلال نافذة شقة مريحة من غرفتي نوم في سان فرانسيسكو ، ينظر إلينا وادي السيليكون الشهير ، كاليفورنيا ، الولايات المتحدة الأمريكية. نعم ، هذا هو سبب عدم الكتابة عمليًا مؤخرًا. تحركنا.

بدأ كل شيء في أبريل 2011 عندما كنت أجري مقابلة عبر الهاتف في Zynga. ثم بدا الأمر وكأنه نوع من الألعاب لا علاقة له بالواقع ، ولم أستطع حتى تخيل ما سينتج عنه. في يونيو 2011 ، جاءت Zynga إلى موسكو وأجرت سلسلة من المقابلات ، وتم النظر في حوالي 60 مرشحًا اجتازوا المقابلات الهاتفية ، وتم اختيار حوالي 15 منهم (لا أعرف الرقم الدقيق ، غير شخص ما رأيه لاحقًا ، شخص ما على الفور رفض). اتضح أن المقابلة كانت بسيطة بشكل مدهش. لا توجد مهام برمجية ، ولا أسئلة صعبة حول شكل الفتحات ، ومعظمها تم اختبار القدرة على الدردشة. والمعرفة ، في رأيي ، تم تقييمها بشكل سطحي فقط.

ثم بدأت الحيلة. أولاً ، انتظرنا النتائج ، ثم العرض ، ثم موافقة LCA ، ثم الموافقة على عريضة الحصول على تأشيرة ، ثم المستندات من الولايات المتحدة ، ثم قائمة الانتظار في السفارة ، ثم شيك إضافي ، ثم تأشيرة. بدا لي أحيانًا أنني مستعد لإسقاط كل شيء وإحراز الأهداف. في بعض الأحيان كنت أشك فيما إذا كنا بحاجة إلى أمريكا هذه ، بعد كل شيء ، إنها ليست سيئة في روسيا أيضًا. استغرقت العملية بأكملها حوالي ستة أشهر ، ونتيجة لذلك ، تلقينا في منتصف ديسمبر التأشيرات وبدأنا في الاستعداد للمغادرة.

كان يوم الاثنين أول يوم لي في العمل. المكتب لديه جميع الشروط ليس فقط للعمل ، ولكن أيضًا للمعيشة. وجبات الإفطار والغداء والعشاء من طهاتنا ، ومجموعة من الأطعمة المتنوعة مكتظة في كل مكان ، وصالة رياضية ، ومساج وحتى مصفف شعر. كل هذا مجاني تمامًا للموظفين. يذهب الكثير من الناس إلى العمل بالدراجة وهناك عدة غرف لتخزين المركبات. بشكل عام ، لم أجد شيئًا كهذا في روسيا. ومع ذلك ، كل شيء له سعره الخاص ، وقد حذرنا على الفور من أنه سيتعين علينا العمل كثيرًا. ما هو "الكثير" ، وفقًا لمعاييرهم ، ليس واضحًا جدًا بالنسبة لي.

ومع ذلك ، آمل ، على الرغم من حجم العمل ، أن أكون قادرًا على استئناف التدوين في المستقبل المنظور وربما أخبرك شيئًا عن الحياة الأمريكية والعمل كمبرمج في أمريكا. انتظر و شاهد. في غضون ذلك ، أهنئ الجميع بالعام الجديد وعيد الميلاد القادم وأراكم قريبًا!

للحصول على مثال للاستخدام ، سنطبع عائد توزيعات أرباح الشركات الروسية. كسعر أساسي ، نأخذ سعر إغلاق السهم في يوم إغلاق السجل. لسبب ما ، هذه المعلومات ليست على موقع الترويكا ، لكنها أكثر إثارة للاهتمام من القيم المطلقة للأرباح.
انتباه! يستغرق تنفيذ الكود وقتًا طويلاً ، لأن لكل ترقية ، تحتاج إلى تقديم طلب إلى خوادم finam والحصول على قيمتها.

نتيجة<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0) (جرب ((اقتباسات<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0) (ي<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

وبالمثل ، يمكنك تكوين إحصائيات للسنوات الماضية.

بطريقة ما حدث ذلك لدرجة أنني أحب حقًا جميع أنواع الخوارزميات التي لها تبرير رياضي واضح ومنطقي) ولكن غالبًا ما يكون وصفها على الإنترنت محملاً بالصيغ والحسابات لدرجة أنه من المستحيل فهم المعنى العام للخوارزمية. لكن فهم جوهر ومبدأ تشغيل الجهاز / الآلية / الخوارزمية أهم بكثير من حفظ الصيغ الضخمة. مهما كانت مبتذلة ، فإن حفظ حتى مئات الصيغ لن يساعد في أي شيء إذا كنت لا تعرف كيف وأين تطبقها 😉 في الواقع ، ما الغرض من كل هذا .. قررت التلاعب في وصف بعض الخوارزميات التي كان عليّ التعامل معها مع في الممارسة. سأحاول عدم التحميل الزائد بالحسابات الرياضية ، بحيث تكون المادة واضحة والقراءة سهلة.

واليوم سنتحدث عنه مرشح كالمانفلنكتشف ما هو ولماذا وكيف يتم استخدامه.

لنبدأ بمثال صغير. دعونا نواجه مهمة تحديد تنسيق الطائرة الطائرة. علاوة على ذلك ، بالطبع ، يجب تحديد التنسيق (دعونا نحدده) بأكبر قدر ممكن من الدقة.

على متن الطائرة ، قمنا بتثبيت جهاز استشعار مسبقًا ، والذي يمنحنا بيانات الموقع المطلوبة ، ولكن ، مثل كل شيء في هذا العالم ، فإن مستشعرنا ليس مثاليًا. لذلك ، بدلاً من القيمة ، نحصل على:

أين خطأ المستشعر ، أي متغير عشوائي. وبالتالي ، من القراءات غير الدقيقة لمعدات القياس ، يجب أن نحصل على قيمة الإحداثيات () في أقرب وقت ممكن من الموضع الحقيقي للطائرة.

تم طرح المشكلة ، دعنا ننتقل إلى حلها.

دعنا نعرف إجراء التحكم () ، الذي بفضله تطير الطائرة (أخبرنا الطيار بأي رافعات يسحبها 😉). بعد ذلك ، بمعرفة الإحداثي عند الخطوة k ، يمكننا الحصول على القيمة عند (k + 1) الخطوة:

يبدو أن هذا هو ما تحتاجه! وليس هناك حاجة إلى مرشح كالمان هنا. لكن ليس كل شيء بهذه البساطة .. في الواقع ، لا يمكننا أن نأخذ في الاعتبار جميع العوامل الخارجية التي تؤثر على الرحلة ، لذلك تأخذ الصيغة الشكل التالي:

أين هو خطأ ناتج عن تأثيرات خارجية ، ونقص في المحرك ، وما إلى ذلك.

إذن ماذا يحدث؟ في الخطوة (k + 1) ، لدينا ، أولاً ، قراءة مستشعر غير دقيقة ، وثانيًا ، قيمة محسوبة بشكل غير دقيق تم الحصول عليها من القيمة في الخطوة السابقة.

فكرة مرشح كالمان هي الحصول على تقدير دقيق للإحداثيات المرغوبة (لحالتنا) من قيمتين غير دقيقين (أخذهما مع معاملات وزن مختلفة). بشكل عام ، يمكن أن تكون القيمة المقاسة مطلقًا (درجة الحرارة ، السرعة ..). إليك ما يحدث:

من خلال الحسابات الرياضية ، يمكننا الحصول على صيغة لحساب معامل كالمان في كل خطوة ، ولكن ، كما هو متفق عليه في بداية المقال ، لن نتعمق في الحسابات ، خاصةً أنه قد ثبت عمليًا أن معامل كالمان دائمًا يميل إلى قيمة معينة مع زيادة k. نحصل على أول تبسيط لصيغتنا:

افترض الآن أنه لا يوجد اتصال مع الطيار ، ولا نعرف إجراء التحكم. يبدو أنه في هذه الحالة لا يمكننا استخدام مرشح كالمان ، لكن هذا ليس كذلك 😉 نحن ببساطة "نتخلص" من الصيغة ما لا نعرفه ، إذن

نحصل على صيغة كالمان الأكثر بساطة ، والتي ، على الرغم من هذه التبسيط "الصعبة" ، تتواءم مع مهمتها بشكل مثالي. إذا كنت تمثل النتائج بيانياً ، فستحصل على شيء مشابه لما يلي:

إذا كان المستشعر الخاص بنا دقيقًا للغاية ، فمن الطبيعي أن يكون عامل الترجيح K قريبًا من واحد. إذا كان الوضع معاكسًا ، أي أن المستشعر الخاص بنا ليس جيدًا جدًا ، فيجب أن يكون K أقرب إلى الصفر.

ربما هذا كل شيء ، هكذا اكتشفنا للتو خوارزمية ترشيح كالمان! آمل أن تكون المقالة مفيدة وواضحة =)