Bringing to a stepped form with the solution. Cutting the matrix to a stepped form. Elementary rows and columns transformations. Criterion of linear dependence of vectors
To bring the matrix to a stepped type (Fig. 1.4), you need to perform the following steps.
1. In the first column, select an element other than zero ( lead element ). A string with a leading element ( leading string ) if it is not the first, to rearrange in the first line (conversion I type). If there is no master in the first column (all the elements are zero), then we exclude this column, and continue to search for the lead element in the remainder of the matrix. The conversion ends if all columns are excluded or in the remaining part of the matrix all zero elements.
2. Split all elements of the host string to the lead element (type II transformation). If the leading line is the latter, then on this transformation should be finished.
3. To each row located below the lead, add a leading line multiplied by such a number, respectively, so that the elements that stand under the lead are equal to zero (type III transformation).
4. By eliminating the line and column from consideration, on whose intersection is the leading element, go to clause 1, in which all the actions described are applied to the remainder of the matrix.
7. The theorem is about the row of a row of a row of elemented elements.
The definition theorem for the elements of a string or column allows you to reduce the calculation of the determinant - order () to calculate the procedure determinants .
If the determinant has equal zero elements, then the most convenient to decompose the determinant for the elements of the row or column, which contains the largest number of zeros.
Using the properties of determinants, you can convert the determinant - the order so that all the elements of some row or column, except one, become equal to zero. Thus, the calculation of the determinant - order, if it is different from zero, will be reduced to the calculation of one determinant - order.
Task 3.1.Calculate the determinant
Decision. Adding the first line first, to the third - the first, multiplied by 2, to the fourth - the first, multiplied by -5, we get
Decomposing the determinant for the elements of the first column, we have
In the resulting determinant of the 3rd order, we turn into zero all the elements of the first column, except for the first one. To do this, the second line will add the first, multiplied by (-1), to the third, multiplied by 5, add the first, multiplied by 8. Since the third line was multiplied by 5, then (in order for the determinant not to change) to multiply it on . Have
The resulting determinant will be decomposed on the elements of the first column:
8. Laplace Theorem (1). Theorem About Stranki Dopname (2)
1) Identifies the determination of the elements of any row on their iaalgebracy.
2) Summary of the elements of the determinant for algebraic supplements of the corresponding elements of the other line is zero (the multiplication theorem on other people's algebraic supplements).
9. Arithmetic vector darling.
Any point on the plane under the selected coordinate system is given by a pair (α, β) of its coordinates; The numbers α and β can also be understood as the coordinates of the radius-vector with the end at this point. Similarly, in the Troika space (α, β, γ) determines the point or vector with the coordinates α, β, γ. This is based on a well-known reader the geometric interpretation of systems of linear equations with two or three unknowns. So, in the case of a system of two linear equations with two unknown
a 1 x + B 1 y \u003d C 1,
a 2 x + b 2 y \u003d c 2
each of the equations is interpreted as straight on the plane (see Fig. 26), and the solution (α, β) is as a point of intersection of these direct or as a vector with AIR coordinates (the figure corresponds to the case when the system has a single solution).
Fig. 26.
Similarly, you can enroll with the system of linear equations with three unknown, interpreting each equation as the equation of the plane in space.
In mathematics and various applications (in particular, in coding theory), it is necessary to deal with systems of linear equations containing more than three unknown. The system of linear equations with n unknown x 1, x 2, ..., x n is called a set of equations of the species
a 11 x 1 + a 12 x 2 + ... + and 1n x n \u003d b 1,
a 21 x 1 + a 22 x 2 + ... + a 2n x n \u003d b 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
and m1 x 1 + and m2 x 2 + ... + and mn x n \u003d b m,
where A IJ and B I are arbitrary valid numbers. The number of equations in the system can be anyone and is not associated with the number of unknown. The coefficients at unknown and ij have a double numbering: the first index I indicates the number of the equation, the second index j is the number of the unknown, which costs this coefficient. Any solution of the system is understood as a set (valid) of the values \u200b\u200bof unknown (α 1, α 2, ..., α n), energizing each equation in faithful equality.
Although the direct geometric interpretation of the system (1) at N\u003e 3 is no longer possible, but it is quite possible and in many ways it is convenient to extend to an arbitrary N geometric language of the space of two or three dimensions. This goal and serve further definitions.
Any ordered set of n valid numbers (α 1, α 2, ..., α n) is called a N-dimensional arithmetic vector, and the numbers α 1, α 2, ..., α n coordinates of this vector.
For the designation of vectors, it is used, as a rule, bold and for the vector A with the coordinates α 1, α 2, ..., α n is preserved ordinary form Records:
a \u003d (α 1, α 2, ..., α n).
By analogy with a conventional plane, the set of all n-dimensional vectors that satisfy the linear equation with n unknown are called the hyperplane in N-dimensional space. With this definition, the set of all solutions of the system (1) is nothing but the intersection of several hyperplanes.
Addition and multiplication of N-dimensional vectors are determined by the same rules as for conventional vectors. Namely, if
a \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Two n-dimensional vector, then their sum is called vector
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
The product of the vector and the number λ is called vector
λа \u003d (λα 1, λα 2, ..., λα n). (four)
The set of all N-dimensional arithmetic vectors with the operations of the addition of vectors and multiplication of the vector is called an arithmetic N-dimensional vector space L n.
Using the operations entered, it is possible to consider arbitrary linear combinations of several vectors, i.e. the expression
λ 1 a 1 + λ 2 a 2 + ... + λ k a k,
where λ i is valid numbers. For example, a linear combination of vectors (2) with coefficients λ and μ is a vector
λа + μB \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
In the three-dimensional space of vectors, the top of the vectors I, J, K (coordinate orthops) play a special role, which is decomposed by any vector A:
a \u003d xi + yj + zk,
where x, y, z are valid numbers (the coordinates of the vector a).
In n-dimensional case, the following vectors play the same role:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Every vector A is, obviously, a linear combination of vectors E 1, E 2, ..., E N:
a \u003d a 1 e 1 + a 2 e 2 + ... + a n e n, (6)
moreover, the coefficients α 1, α 2, ..., α n coincide with the coordinates of the vector a.
Denote by 0 vector, all coordinates of which are zero (briefly, zero vector), we introduce the following important definition:
The system of vectors A 1, and 2, ..., and K is called linearly dependent, if there is an equal to zero vector linear combination
λ 1 a 1 + λ 2 a 2 + ... + λ k a k \u003d 0,
in which at least one of the coefficients H 1, λ 2, ..., λ k is different from zero. Otherwise, the system is called linearly independent.
So, vectors
a 1 \u003d (1, 0, 1, 1), a 2 \u003d (1, 2, 1, 1), and 3 \u003d (2, 2, 2, 2)
linearly dependent because
a 1 + a 2 - a 3 \u003d 0.
Linear dependence, as can be seen from the definition, is equivalent (at k ≥ 2) to the fact that at least one of the system vectors is a linear combination of the remaining.
If the system consists of two vectors A 1, a 2, then the linear dependence of the system means that one of the vectors is proportional to another, say, and 1 \u003d λa 2; In a three-dimensional case, it is equivalent to the collinearity of vectors A 1 and A 2. Similarly, the linear dependence of the system I of three vectors in conventional space means the compatination of these vectors. Concept linear dependence It is thus the natural generalization of the concepts of collinearity and comparity.
It is easy to make sure that the vectors E 1, E 2, ..., e n from the system (5) are linearly independent. Therefore, there are systems from N linearly independent vectors in N-dimensional space. It can be shown that any system of larger number of vectors is linearly dependent.
Any System A 1, A 2, ..., and n from n linearly independent vectors of the N-dimensional space L N is called its basis.
Any vector and the spaces L n unfolds, and moreover, by the vector of an arbitrary basis A 1, and 2, ..., and n:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ n a n.
This fact is easily established based on the definition of the basis.
Continuing an analogy with a three-dimensional space, it is possible in the n-dimensional case to determine the scalar product A · B of vectors, believing
a · B \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
With this definition, all the basic properties of the scalar product of three-dimensional vectors are preserved. Vectors A and B are called orthogonal if their scalar product is zero:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
In the theory of linear codes, another important concept is used - the concept of subspace. Subset of V space L N is called the subspace of this space if
1) for any vectors A, B, belonging to V, their sum A + B also belongs to V;
2) for any vector A, belonging to V, and for any actual number λ, the vector λa also belongs to V.
For example, the set of all linear combinations of vectors E 1, E 2 from the system (5) will be a subspace of the space L n.
In a linear algebra, it is proved that in every subspace V, there is such a linearly independent system of vectors A 1, a 2, ..., a k, which every vector and subspace is a linear combination of these vectors:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ k a k.
The specified system of vectors is called the basis of the subspace V.
From the definition of space and subspace immediately follows that the space L n is the commutative group relative to the formation of vectors, and any of its subspace V is a subgroup of this group. In this sense, it is possible, for example, to consider the adjacent classes of space L N by subspace V.
In conclusion, we emphasize that if in the theory of N-dimensional arithmetic space instead of valid numbers (i.e., the elements of the field of valid numbers) consider the elements of an arbitrary field F, then all the definitions and the facts given above would have retained strength.
In the coding theory, an important role plays the case when the field F field of deduction z p, which, as we know, of course. In this case, the corresponding N-dimensional space also contains, as it is not difficult to see, p n elements.
The concept of space, as well as the concept of a group and rings, also allows an axiomatic definition. For details, we send the feeder to any course of a linear algebra.
10. Lynіin Combіnatsiya. Lynіino Zarezhnі Tu inepless system vector.
In this topic, consider the concept of the matrix, as well as types of matrices. Since there are many terms in this topic, I will add summaryTo navigate in the material it was easier.
Definition of the matrix and its element. Designations.
The matrix - This is a table of $ M $ rows and $ n $ columns. Objects of the matrix may be objects of a completely diverse nature: numbers, variables or, for example, other matrices. For example, the $ \\ left matrix (\\ begin (Array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right) $ contains 3 lines and 2 columns; Its elements are integers. Matrix $ \\ left (\\ Begin (Array) (CCCC) A & A ^ 9 + 2 & 9 & SIN X \\\\ -9 & 3T ^ 2-4 & UT & 8 \\ END (Array) \\ Right) $ Contains 2 lines and 4 columns.
Different ways to recording matrices: show / hide
The matrix can be recorded not only in round, but also in square or double direct brackets. Below is the same matrix in various form of recording:
$$ \\ left (\\ begin (array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right); \\; \\; \\ left [\\ begin (array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right]; \\; \\; \\ Left \\ Vert \\ Begin (Array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right \\ Vert $$
The product $ M \\ Times N $ is called the size of the matrix. For example, if the matrix contains 5 lines and 3 columns, then they say about the matrix of the size of $ 5 \\ Times $ 3. Matrix $ \\ Left (\\ Begin (Array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ End (Array) \\ Right) $ has a size of $ 3 \\ Times $ 2.
Typically, the matrices are designated by the large letters of the Latin alphabet: $ a $, $ b $, $ C $ and so on. For example, $ B \u003d \\ Left (\\ Begin (Array) (CCC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right) $. The numbering of strings is topped down; Columns - from left to right. For example, the first line of the $ b $ matrix contains elements 5 and 3, and the second column contains elements 3, -87, 0.
The elements of the matrices are usually denoted by small letters. For example, the elements of the $ a $ matrix are denoted $ a_ (ij) $. Dual index $ ij $ contains information about the position of the element in the matrix. The number $ i $ is the number of the line, and the number $ j $ is the number of the column, on the intersection of which there is an element $ A_ (IJ) $. For example, at the intersection of the second line and the fifth column of the matrix $ A \u003d \\ LEFT (\\ Begin (Array) (CCCCCC) 51 & 37 & -9 & 0 & 9 & 97 \\\\ 1 & 2 & 3 & 41 & 59 & 6 \\ $ 59:
In the same way, at the intersection of the first line and the first column we have an element $ A_ (11) \u003d $ 51; At the intersection of the third row and the second column - the element $ A_ (32) \u003d - $ 15 and so on. I note that the record $ a_ (32) $ is read as "and three two", but not "and thirty two".
For the abbreviated designation of the matrix $ a $, the size of which is $ M \\ Times N $, is used to record $ A_ (M \\ Times N) $. It is often used and such a record:
$$ A_ (M \\ Times (n)) \u003d (A_ (ij)) $$
Here $ (A_ (ij)) $ indicates the designation of the elements of the matrix $ a $, i.e. It suggests that the elements of the $ a $ matrix are referred to as $ A_ (IJ) $. In the deployment form of the matrix $ A_ (M \\ Times N) \u003d (A_ (IJ)) $ can be written as:
$$ A_ (M \\ Times N) \u003d \\ Left (\\ Begin (Array) (CCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1N) \\\\ A_ (21) & A_ (22) & \\ LDOTS & A_ (2N) \\\\ \\ Ldots & \\ Ldots & \\ Ldots & \\ Ldots \\\\ A_ (M1) & A_ (M2) & \\ LDOTS & A_ (MN) \\ END (Array) \\ Right) $$
We introduce another term - equal matrices.
Two matrices of the same size $ A_ (M \\ Times N) \u003d (A_ (IJ)) $ and $ B_ (M \\ Times N) \u003d (B_ (IJ)) $ called equalif their respective elements are equal, i.e. $ A_ (ij) \u003d b_ (ij) $ for all $ i \u003d \\ Overline (1, M) $ and $ j \u003d \\ Overline (1, N) $.
Explanation of the record $ i \u003d \\ Overline (1, M) $: show / hide
Recording "$ i \u003d \\ Overline (1, M) $" means that the $ i $ parameter varies from 1 to m. For example, the record $ i \u003d \\ Overline (1.5) $ indicates that the parameter $ i $ takes values \u200b\u200b1, 2, 3, 4, 5.
So, for the equality of matrices, the execution of two conditions is required: coincidence of the size and equality of the corresponding elements. For example, the matrix $ a \u003d \\ left (\\ begin (array) (CC) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right) $ is not equal to the matrix $ B \u003d \\ left (\\ $ 2. Also, the $ a $ matrix is \u200b\u200bnot equal to the $ c \u003d \\ left matrix (\\ begin (array) (CC) 5 & 3 \\\\ 98 & -87 \\\\ 8 & 0 \\ END (Array) \\ Right) $, since $ A_ ( 21) \\ NEQ C_ (21) $ (i.e. $ 0 \\ NEQ $ 98). But for the matrix $ f \u003d \\ left (\\ begin (array) (CC) 5 & 3 \\ ED (Array) \\ Right) $ can boldly burn $ a \u003d F $ since and dimensions, and the corresponding elements of the matrices $ a $ and $ F $ coincide.
Example №1
Determine the size of the matrix $ a \u003d \\ left (\\ begin (array) (CCC) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\\\ -6 & 8 & 23 \\\\ 11 & -12 & -5 \\ Indicate what is equal to the elements $ A_ (12) $, $ A_ (33) $, $ A_ (43) $.
This matrix contains 5 lines and 3 columns, so the size of its $ 5 \\ Times $ 3. For this matrix, you can also use the designation $ A_ (5 \\ Times 3) $.
An element $ A_ (12) $ is at the intersection of the first line and the second column, therefore $ A_ (12) \u003d - $ 2. An element $ A_ (33) $ is at the intersection of the third line and the third column, therefore $ A_ (33) \u003d 23 $. The element $ A_ (43) $ is at the intersection of the fourth line and the third column, therefore $ A_ (43) \u003d - $ 5.
Answer: $ A_ (12) \u003d - 2 $, $ A_ (33) \u003d 23 $, $ A_ (43) \u003d - $ 5.
Types of matrices depending on their size. Home and side diagonal. Matrix mark.
Let a certain matrix of $ A_ (M \\ Times N) $. If $ m \u003d 1 $ (the matrix consists of one row), then the specified matrix is \u200b\u200bcalled matrix-string. If $ n \u003d 1 $ (the matrix consists of one column), then such a matrix is \u200b\u200bcalled matrix-column. For example, $ \\ left (\\ begin (array) (CCCCC) -1 & -2 & 0 & -9 & 8 \\ END (Array) \\ Right) $ - matrix-string, and $ \\ left (\\ begin (array) (C) -1 \\\\ 5 \\\\ 6 \\ END (Array) \\ Right) $ - column matrix.
If the matrix $ A_ (M \\ Times N) $ is correct to the $ M \\ NE $ condition (i.e., the number of rows is not equal to the number of columns), then it is often said that $ a $ is a rectangular matrix. For example, the $ \\ Left matrix (\\ Begin (Array) (CCCC) -1 & -2 & 0 & 9 \\\\ 5 & 9 & 5 & 1 \\ End (Array) \\ Right) $ has a size $ 2 \\ Times $ 4 those. Contains 2 lines and 4 columns. Since the number of rows is not equal to the number of columns, then this matrix is \u200b\u200brectangular.
If for the matrix $ a_ (m \\ times n) $, the condition is $ m \u003d n $ (i.e., the number of rows is equal to the number of columns), then they say that $ a $ is a square matrix of about $ n $. For example, $ \\ left (\\ begin (array) (CC) -1 & -2 \\\\ 5 & 9 \\ END (Array) \\ Right) $ is a second-order square matrix; $ \\ left (\\ begin (array) (CCC) -1 & -2 & 9 \\\\ 5 & 9 & 8 \\\\ 1 & 0 & 4 \\ END (Array) \\ Right) $ is a third-order square matrix. In general, the square matrix $ A_ (N \\ Times N) $ can be recorded like this:
$$ A_ (N \\ Times N) \u003d \\ Left (\\ Begin (Array) (CCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1N) \\\\ A_ (21) & A_ (22) & \\ LDOTS & A_ (2N) \\\\ \\ Ldots & \\ Ldots & \\ Ldots & \\ Ldots \\\\ A_ (N1) & A_ (N2) & \\ Ldots & A_ (NN) \\ END (Array) \\ Right) $$
It is said that the elements $ a_ (11) $, $ A_ (22) $, $ \\ ldots $, $ A_ (NN) $ are on main diagonal Matrix $ A_ (N \\ Times N) $. These elements are called the main diagonal elements (or simply diagonal elements). Elements $ A_ (1N) $, $ A_ (2 \\; N-1) $, $ \\ ldots $, $ A_ (N1) $ are on side (secondary) diagonal; they are called by-diagonal elements. For example, for the matrix $ C \u003d \\ Left (\\ Begin (Array) (CCCC) 2 & 9 & 9 & 1 \\\\ 5 & 9 & 8 & 0 \\\\ 1 & 0 & 4 & 6 \\ END (Array) \\ Right) $ We have:

Elements $ C_ (11) \u003d 2 $, $ C_ (22) \u003d 9 $, $ C_ (33) \u003d $ 4, $ C_ (44) \u003d $ 6 are the main diagonal elements; Elements $ C_ (14) \u003d 1 $, $ C_ (23) \u003d $ 8, $ C_ (32) \u003d 0 $, $ C_ (41) \u003d - $ 4 - Side diagonal elements.
The sum of the main diagonal elements is called following the matrix and denotes $ \\ tr a $ (or $ \\ sp a $):
$$ \\ TR A \u003d A_ (11) + A_ (22) + \\ LDOTS + A_ (NN) $$
For example, for the matrix $ C \u003d \\ Left (\\ Begin (Array) (CCCC) 2 & -2 & 9 & 1 \\\\ 5 & 9 & 8 & 0 \\\\ 1 & 0 & 4 & -7 \\\\ - 4 & 4 & -9 & 5 & 6 \\ End (Array) \\ Right) $ We have:
$$ \\ TR C \u003d 2 + 9 + 4 + 6 \u003d 21. $$.
The concept of diagonal elements is also used for non-commercial matrices. For example, for the matrix $ B \u003d \\ left (\\ Begin (Array) (CCCCC) 2 & -2 & 9 & 1 & 7 \\\\ 5 & -9 & 0 & 4 & - 6 \\\\ 1 & 0 & 4 & - 7 & -6 \\ END (Array) \\ Right) $ Main diagonal elements will be $ b_ (11) \u003d 2 $, $ b_ (22) \u003d - 9 $, $ b_ (33) \u003d $ 4.
Types of matrices depending on the values \u200b\u200bof their elements.
If all the elements of the matrix $ A_ (M \\ Times N) $ are zero, then such a matrix is \u200b\u200bcalled null And it is usually denoted by the letter $ o $. For example, $ \\ left (\\ begin (array) (CC) 0 & 0 \\\\ 0 & 0 \\\\ 0 & 0 \\ END (Array) \\ Right) $, $ \\ left (\\ begin (array) (CCC) 0 & 0 \\\\ 0 & 0 \\ ED (Array) \\ Right) $ - zero matrices.
Consider some non-zero string of the $ a $ matrix, i.e. Such a string in which there is at least one element other than zero. Lead element The nonzero line will call it first (counting from left to right) a nonzero element. For example, consider such a matrix:
$$ w \u003d \\ left (\\ begin (Array) (CCCC) 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 12 \\ ED (Array) \\ Right) $ $
In the second line the lead will be the fourth element, i.e. $ w_ (24) \u003d 12 $, and in the third line the master will be the second element, i.e. $ w_ (32) \u003d - $ 9.
Matrix $ A_ (M \\ Times N) \u003d \\ Left (A_ (ij) \\ Right) $ called speedIf it satisfies two conditions:
- Zero lines, if any, are located below all non-zero lines.
- The numbers of the leading elements of non-zero rows form a strictly increasing sequence, i.e. If $ A_ (1K_1) $, $ A_ (2K_2) $, ..., $ A_ (rk_r) $ - the leading elements of non-zero lines of the matrix $ a $, then $ k_1 \\ lt (k_2) \\ l \\ ldots \\ lt ( k_r) $.
Examples of stepped matrices:
$$ \\ Left (\\ Begin (Array) (CCCCCC) 0 & 0 & 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ END (Array) \\ Right); \\; \\ Left (\\ Begin (Array) (CCCC) 5 & -2 & 2 & -8 \\\\ 0 & 4 & 0 & 0 \\ ED (Array) \\ Right). $$.
For comparison: Matrix $ Q \u003d \\ Left (\\ Begin (Array) (CCCCC) 2 & -2 & 0 & 1 & 9 \\\\ 0 & 0 & 0 & 7 & 9 \\\\ 0 & 0 & 0 & 10 & 10 & 6 \\ END (Array) \\ Right) $ is not a stepped, since the second condition is broken in determining the stepped matrix. The leading elements in the second and third lines $ Q_ (24) \u003d 7 $ and $ q_ (32) \u003d $ 10 have numbers $ k_2 \u003d $ 4 and $ k_3 \u003d $ 2. For a stepped matrix, the condition $ k_2 \\ lt (k_3) $ must be performed, which in this case is impaired. I note that if you change the second and third lines in places, we will get a stepped matrix: $ \\ left (\\ Begin (Array) (CCCCC) 2 & -5 & 0 & 1 & 9 \\\\ 0 & -5 & 0 & 10 \\\\ 0 & 0 & 0 & 7 & 9 \\ END (Array) \\ Right) $.
A stepped matrix is \u200b\u200bcalled trapezoidal or trapezoidalif for the leading elements $ a_ (1k_1) $, $ a_ (2k_2) $, ..., $ a_ (rk_r) $ Conditions of $ k_1 \u003d 1 $, $ k_2 \u003d 2 $, ..., $ k_r \u003d R $, i.e. Diagonal elements are leading. In general, the trapezoid matrix can be written as follows:
$$ A_ (M \\ Times (N)) \u003d \\ Left (\\ Begin (Array) (CCCCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1R) & \\ LDOTS & A_ (1N) \\\\ A_ (RR) \\ LDOTS & A_ (RN) \\\\ 0 & 0 & 0 \\ LDOTS & 0 & 0 & 0 \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS \\\\ 0 & 0 \\ LDOTS & 0 & \\ LDOTS & 0 \\ END (Array) \\ Right) $$
Examples of trapezoidal matrices:
$$ \\ left (\\ Begin (Array) 4 & 0 & 0 & -4 & 1 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 \\\\ 0 & 0 & 0 & 0 & 0 \\ END (Array) \\ Right); \\; \\ Left (\\ Begin (Array) (CCCC) 5 & -2 & 2 & -8 \\\\ 0 & 4 & 0 & 0 \\ ED (Array) \\ Right). $$.
Let's give a few more definitions for square matrices. If all items square matrixlocated under the main diagonal are zero, then such a matrix is \u200b\u200bcalled upper triangular matrix. For example, $ \\ left (\\ Begin (Array) (CCCC) 2 & -2 & 9 & 1 \\\\ 0 & 9 & 8 & 0 \\\\ 0 & 0 & 4 & 6 \\\\ 0 & 0 & 6 \\ END (Array) \\ Right) $ - upper triangular matrix. Notice that in the definition of the upper triangular matrix, nothing is said about the values \u200b\u200bof the elements located above the main diagonal or on the main diagonal. They can be zero or not, is insignificant. For example, $ \\ left (\\ begin (array) (CCC) 0 & 0 & 9 \\\\ 0 & 0 & 0 \\\\ 0 & 0 \\ END (Array) \\ Right) $ is also an upper triangular matrix.
If all the elements of the square matrix, located above the main diagonal, are zero, then such a matrix is \u200b\u200bcalled lower triangular matrix. For example, $ \\ left (\\ Begin (Array) (CCCC) 3 & 0 & 0 & 0 \\\\ -5 & 1 & 0 & 0 \\\\ 8 & 2 & 1 & 0 \\\\ 5 & 4 & 0 & 6 \\ Note that in defining the lower triangular matrix, nothing is said about the values \u200b\u200bof the elements located under or on the main diagonal. They can be zero or not, it does not matter. For example, $ \\ left (\\ Begin (Array) (CCC) -5 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 9 \\ END (Array) \\ Right) $ and $ \\ left (\\ begin (Array) (CCC) 0 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \\ END (Array) \\ Right) $ - also lower triangular matrices.
Square matrix is \u200b\u200bcalled diagonalIf all the elements of this matrix that are not lying on the main diagonal are zero. Example: $ \\ left (\\ begin (array) (CCCC) 3 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 6 \\ Elements on the main diagonal can be any (equal zero or not), is insignificant.
Diagonal matrix is \u200b\u200bcalled singleIf all the elements of this matrix located on the main diagonal are equal to 1. For example, $ \\ left (\\ begin (Array) (CCCC) 1 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 \\ END (Array) \\ Right) $ is a single fourth order matrix; $ \\ left (\\ begin (array) (CC) 1 & 0 \\\\ 0 & 1 \\ END (Array) \\ Right) $ is a single second-order matrix.
In July 2020, NASA launches an expedition to Mars. The spacecraft will deliver an electronic media to Mars with the names of all registered expedition participants.
Registration of participants is open. Get your ticket for Mars for this link.
If this post decided your problem or just liked you, share a link to it with my friends on social networks.
One of these code options must be copied and insert into the code of your webpage, preferably between the tags
and or immediately after the tag . According to the first version, MathJax is loaded faster and slows down the page. But the second option automatically tracks and loads the latest MathJax versions. If you insert the first code, it will need to be periodically updated. If you insert the second code, the pages will be loaded slower, but you will not need to constantly monitor MathJax updates.Connect MathJax is the easiest way to Blogger or WordPress: Add a widget for inserting a third-party JavaScript code to insert the first or second version of the download code presented above and place the widget closer to the beginning of the template (by the way, it is not at all necessary Since the MathJax script is loaded asynchronously). That's all. Now read the Mathml, LaTEX and ASCIIMATHML markup syntax, and you are ready to insert mathematical formulas On the web pages of your site.
Another New Year's Eve ... Frosty Weather and Snowflakes on the window glass ... All this prompted me to again write about ... Fractals, and about what he knows about this Alpha tungshes. On this occasion, there is an interesting article in which there are examples of two-dimensional fractal structures. Here we will consider more complex examples of three-dimensional fractals.
The fractal can be clearly imagined (describe), as a geometric shape or body (having in mind that both there are many, in this case, a set of points), the details of which have the same shape as the original figure itself. That is, it is a self-like structure, considering the details of which with an increase, we will see the same form as without increasing. Whereas in the case of a conventional geometric shape (not fractal), with an increase we will see the details that have more simple shapethan the original figure itself. For example, with a sufficiently large increase, the part of the ellipse looks like a straight line. With fractals, this does not happen: with any increases, we will again see the same complex shape, which will repeat again and again.
Benoit Mandelbrot (Benoit Mandelbrot), the founder of the science of fractals, in his article Fractals and art in the name of science wrote: "Fractals are geometric forms that are equally complex in their details, as in its general form. That is, if Part of the fractal will be increased to the size of the whole, it will look like an integer, or exactly, or, possibly, with a small deformation. "
To bring the matrix to a stepped type (Fig. 1.4), you need to perform the following steps.
1. In the first column, select an element other than zero ( lead element ). A string with a leading element ( leading string ) if it is not the first, to rearrange in the first line (conversion I type). If there is no master in the first column (all the elements are zero), then we exclude this column, and continue to search for the lead element in the remainder of the matrix. The conversion ends if all columns are excluded or in the remaining part of the matrix all zero elements.
2. Split all elements of the host string to the lead element (type II transformation). If the leading line is the latter, then on this transformation should be finished.
3. To each row located below the lead, add a leading line multiplied by such a number, respectively, so that the elements that stand under the lead are equal to zero (type III transformation).
4. By eliminating the line and column from consideration, on whose intersection is the leading element, go to clause 1, in which all the actions described are applied to the remainder of the matrix.
The theorem is about the row of a row of a row of element.
The definition theorem for the elements of a string or column allows you to reduce the calculation of the determinant - order () to calculate the procedure determinants .
If the determinant has equal zero elements, then the most convenient to decompose the determinant for the elements of the row or column, which contains the largest number of zeros.
Using the properties of determinants, you can convert the determinant - the order so that all the elements of some row or column, except one, become equal to zero. Thus, the calculation of the determinant - order, if it is different from zero, will be reduced to the calculation of one determinant - order.
Task 3.1.Calculate the determinant
Decision.Adding the first line first, to the third - the first, multiplied by 2, to the fourth - the first, multiplied by -5, we get
Decomposing the determinant for the elements of the first column, we have
![]() .
.
In the resulting determinant of the 3rd order, we turn into zero all the elements of the first column, except for the first one. To do this, the second line will add the first, multiplied by (-1), to the third, multiplied by 5, add the first, multiplied by 8. Since the third line was multiplied by 5, then (in order for the determinant not to change) to multiply it on . Have
The resulting determinant will be decomposed on the elements of the first column:
Laplace Theorem (1). Theorem About Stranki Dopname (2)
1) Identifies the determination of the elements of any row on their iaalgebracy.
2) Summary of the elements of the determinant for algebraic supplements of the corresponding elements of the other line is zero (the multiplication theorem on other people's algebraic supplements).
Any point on the plane under the selected coordinate system is given by a pair (α, β) of its coordinates; The numbers α and β can also be understood as the coordinates of the radius-vector with the end at this point. Similarly, in the Troika space (α, β, γ) determines the point or vector with the coordinates α, β, γ. This is based on a well-known reader the geometric interpretation of systems of linear equations with two or three unknowns. So, in the case of a system of two linear equations with two unknown
a 1 x + B 1 y \u003d C 1,
a 2 x + b 2 y \u003d c 2
each of the equations is interpreted as straight on the plane (see Fig. 26), and the solution (α, β) is as a point of intersection of these direct or as a vector with AIR coordinates (the figure corresponds to the case when the system has a single solution).
 Fig. 26.
Fig. 26.
Similarly, you can enroll with the system of linear equations with three unknown, interpreting each equation as the equation of the plane in space.
In mathematics and various applications (in particular, in coding theory), it is necessary to deal with systems of linear equations containing more than three unknown. The system of linear equations with n unknown x 1, x 2, ..., x n is called a set of equations of the species
a 11 x 1 + a 12 x 2 + ... + and 1n x n \u003d b 1,
a 21 x 1 + a 22 x 2 + ... + a 2n x n \u003d b 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
and m1 x 1 + and m2 x 2 + ... + and mn x n \u003d b m,
where A IJ and B I are arbitrary valid numbers. The number of equations in the system can be anyone and is not associated with the number of unknown. The coefficients at unknown and ij have a double numbering: the first index I indicates the number of the equation, the second index j is the number of the unknown, which costs this coefficient. Any solution of the system is understood as a set (valid) of the values \u200b\u200bof unknown (α 1, α 2, ..., α n), energizing each equation in faithful equality.
Although the direct geometric interpretation of the system (1) at N\u003e 3 is no longer possible, but it is quite possible and in many ways it is convenient to extend to an arbitrary N geometric language of the space of two or three dimensions. This goal and serve further definitions.
Any ordered set of n valid numbers (α 1, α 2, ..., α n) is called a N-dimensional arithmetic vector, and the numbers α 1, α 2, ..., α n coordinates of this vector.
To designate vectors, it is usually bold and for the vector A with coordinates α 1, α 2, ..., α n, a regular form of recording is saved:
a \u003d (α 1, α 2, ..., α n).
By analogy with a conventional plane, the set of all n-dimensional vectors that satisfy the linear equation with n unknown are called the hyperplane in N-dimensional space. With this definition, the set of all solutions of the system (1) is nothing but the intersection of several hyperplanes.
Addition and multiplication of N-dimensional vectors are determined by the same rules as for conventional vectors. Namely, if
a \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Two n-dimensional vector, then their sum is called vector
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
The product of the vector and the number λ is called vector
λа \u003d (λα 1, λα 2, ..., λα n). (four)
The set of all N-dimensional arithmetic vectors with the operations of the addition of vectors and multiplication of the vector is called an arithmetic N-dimensional vector space L n.
Using the operations entered, it is possible to consider arbitrary linear combinations of several vectors, i.e. the expression
λ 1 a 1 + λ 2 a 2 + ... + λ k a k,
where λ i is valid numbers. For example, a linear combination of vectors (2) with coefficients λ and μ is a vector
λа + μB \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
In the three-dimensional space of vectors, the top of the vectors I, J, K (coordinate orthops) play a special role, which is decomposed by any vector A:
a \u003d xi + yj + zk,
where x, y, z are valid numbers (the coordinates of the vector a).
In n-dimensional case, the following vectors play the same role:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Every vector A is, obviously, a linear combination of vectors E 1, E 2, ..., E N:
a \u003d a 1 e 1 + a 2 e 2 + ... + a n e n, (6)
moreover, the coefficients α 1, α 2, ..., α n coincide with the coordinates of the vector a.
Denote by 0 vector, all coordinates of which are zero (briefly, zero vector), we introduce the following important definition:
The system of vectors A 1, and 2, ..., and K is called linearly dependent, if there is an equal to zero vector linear combination
λ 1 a 1 + λ 2 a 2 + ... + λ k a k \u003d 0,
in which at least one of the coefficients H 1, λ 2, ..., λ k is different from zero. Otherwise, the system is called linearly independent.
So, vectors
a 1 \u003d (1, 0, 1, 1), a 2 \u003d (1, 2, 1, 1), and 3 \u003d (2, 2, 2, 2)
linearly dependent because
a 1 + a 2 - a 3 \u003d 0.
Linear dependence, as can be seen from the definition, is equivalent (at k ≥ 2) to the fact that at least one of the system vectors is a linear combination of the remaining.
If the system consists of two vectors A 1, a 2, then the linear dependence of the system means that one of the vectors is proportional to another, say, and 1 \u003d λa 2; In a three-dimensional case, it is equivalent to the collinearity of vectors A 1 and a 2. Similarly, the linear dependence of the system I of three vectors in conventional space means the compatination of these vectors. The concept of linear dependence is thus the natural generalization of the concepts of collinearity and companation.
It is easy to make sure that the vectors E 1, E 2, ..., e n from the system (5) are linearly independent. Therefore, there are systems from N linearly independent vectors in N-dimensional space. It can be shown that any system of larger number of vectors is linearly dependent.
Any System A 1, A 2, ..., and n from n linearly independent vectors of the N-dimensional space L N is called its basis.
Any vector and the spaces L n unfolds, and moreover, by the vector of an arbitrary basis A 1, and 2, ..., and n:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ n a n.
This fact is easily established based on the definition of the basis.
Continuing an analogy with a three-dimensional space, it is possible in the n-dimensional case to determine the scalar product A · B of vectors, believing
a · B \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
With this definition, all the basic properties of the scalar product of three-dimensional vectors are preserved. Vectors A and B are called orthogonal if their scalar product is zero:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
In the theory of linear codes, another important concept is used - the concept of subspace. Subset of V space L N is called the subspace of this space if
1) for any vectors A, B, belonging to V, their sum A + B also belongs to V;
2) for any vector A, belonging to V, and for any actual number λ, the vector λa also belongs to V.
For example, the set of all linear combinations of vectors E 1, E 2 from the system (5) will be a subspace of the space L n.
In a linear algebra, it is proved that in every subspace V, there is such a linearly independent system of vectors A 1, a 2, ..., a k, which every vector and subspace is a linear combination of these vectors:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ k a k.
The specified system of vectors is called the basis of the subspace V.
From the definition of space and subspace immediately follows that the space L n is the commutative group relative to the formation of vectors, and any of its subspace V is a subgroup of this group. In this sense, it is possible, for example, to consider the adjacent classes of space L N by subspace V.
In conclusion, we emphasize that if in the theory of N-dimensional arithmetic space instead of valid numbers (i.e., the elements of the field of valid numbers) consider the elements of an arbitrary field F, then all the definitions and the facts given above would have retained strength.
In the coding theory, an important role plays the case when the field F field of deduction z p, which, as we know, of course. In this case, the corresponding N-dimensional space also contains, as it is not difficult to see, p n elements.
The concept of space, as well as the concept of a group and rings, also allows an axiomatic definition. For details, we send the feeder to any course of a linear algebra.
Lynіin Kombіnatsiya. Lynіino Zarezhnі Tu inepless system vector.
instyer combination of vectors
Linear combination of vectors ![]() call vector
call vector
where ![]() - Linear combination coefficients. If a
- Linear combination coefficients. If a ![]() the combination is called trivial, if non-trivial.
the combination is called trivial, if non-trivial.
Linear dependence and independence of vectors
System ![]() linearly dependent
linearly dependent 
System ![]() linearly independent
linearly independent 
Criterion of linear dependence of vectors
For vectors ![]() (r\u003e 1.) It was linearly dependent, it is necessary and enough so that at least one of these vectors is a linear combination of the rest.
(r\u003e 1.) It was linearly dependent, it is necessary and enough so that at least one of these vectors is a linear combination of the rest.
The dimension of the linear space
Linear space V.called n.- dimensional (has dimension n.), if in it:
1) exists n.linear independent vectors;
2) any system n + 1.the vectors are linearly dependent.
Designations: n.\u003d dim V.;.
The system of vectors is called linearly dependentif exist nenulevaset with a linear combination
The system of vectors is called linearly independentif from equality zero linear combination
it should be equal to zero allcoefficients
The question of the linear dependence of vectors in the general case is reduced to the issue of the existence of a non-zero solution in a homogeneous system of linear equations with coefficients equal to the relevant coordinates of these vectors.
In order to well assign the concept of "linear dependence", "linear independence" system of vectors, it is useful to solve the tasks of the following type:
Lynіin Zarezhnіst.І І ІІ Critia Lіnіinoїni.
System vectors it is linearly dependent then and only if one of the system vectors is a linear combination of the remaining vectors of this system.
Evidence. Let the system of the vectors linearly depend on the vectors. Then there is such a set of coefficients ![]() that, with at least one coefficient differ from zero. Let's pretend that . Then
that, with at least one coefficient differ from zero. Let's pretend that . Then
that is, is a linear combination of the remaining system vectors.
Let one of the system vectors be a linear combination of the remaining vectors. Suppose this is a vector, that is ![]() . It's obvious that . It was obtained that the linear combination of system vectors is zero, and one of the coefficients differ from zero (equal).
. It's obvious that . It was obtained that the linear combination of system vectors is zero, and one of the coefficients differ from zero (equal).
Sentence10 . 7 If the vectors system comprises a linearly dependent subsystem, then the entire system is linearly dependent.
Evidence.
Let in the system of the subsystem vectors ![]() , it is linearly dependent, that is, and at least one coefficient is different from zero. Then make a linear combination. Obviously, this linear combination is zero, and that there is nonzero among the coefficients.
, it is linearly dependent, that is, and at least one coefficient is different from zero. Then make a linear combination. Obviously, this linear combination is zero, and that there is nonzero among the coefficients.
The base system of vector_v, їїsts the authorities.
The base of the nonzero system of vectors is called equivalent to it linearly independent subsystem. The zero system of the base does not have.
Property 1:The base of the linear independent system coincides with it itself.
Example: The system of linear independent vectors Since none of the vectors can be linearly exhaled through the rest.
Property 2: (Criteria base)The linearly independent subsystem of this system is its base if and only if it is most linearly independent.
Evidence:Dana System Necessity Let the base. Then, by definition and, if, where, the system is linearly dependent, since it is linearly perhaps through, hence the most linearly independent. AdequacyLet the most linearly independent subsystem, then where. Linearly dependent linearly exercises through the base of the system.
Property 3: (Basic Base Property)Each system vector is given through the database singly.
EvidenceLet the vector take place through the database in two ways, then:, then
Rank system vector.
|
Definition:The rank of the nonzero system of linear vectors is called the number of vectors of its base. The rank of the zero system by definition is zero. Rank properties:1) The rank of the linearly independent system coincides with the number of its vectors. 2) The rank of the linearly dependent system is less than the number of its vectors. 3) ranks of equivalent systems coincide -Rankrank. 4) The rank under the system is less or equal to rank system. 5) If Rankrank, then the total base. 6) The rank of the system does not change if the vector is added to it, which is a linear combination of the remaining vectors of the system. 7) The rank of the system does not change if the vector is removed from it, which is a linear combination of other vectors. |
To find the rank system of vectors, you need to use the Gaussai method to bring the system to triangular or trapezoidal form.
Ekwіvalent_ system vector.
Example:
We transform the data of the vector in the matrix to find the base. We get: 
Now with the help of the Gauss method, we will convert a matrix to the trapezoidal form:
1) in our main matrix, we will nourish the entire first column, in addition to the first line from the second one, the first multiplied on, from the third one, the first multiplied on, and we will not take anything from the fourth, since the first element of the fourth line, that is, the intersection of the first column and The fourth line is zero. We get a matrix:  2) Now in the matrix, change the lines 2, 3 and 4 to the simplicity of the solution, which would be at the site of the element. I will change the fourth line to put instead of the second, the second instead of the third and third to the fourth place. We get a matrix:
2) Now in the matrix, change the lines 2, 3 and 4 to the simplicity of the solution, which would be at the site of the element. I will change the fourth line to put instead of the second, the second instead of the third and third to the fourth place. We get a matrix:  3) In the matrix, you annul all the elements under the element. Since again, the element of our matre is zero is zero, we are not taking anything from the fourth line, and add the third to the third multiplied by. We get a matrix:
3) In the matrix, you annul all the elements under the element. Since again, the element of our matre is zero is zero, we are not taking anything from the fourth line, and add the third to the third multiplied by. We get a matrix:  4) We again change in the matrix of the string 3 and 4 places. We get a matrix:
4) We again change in the matrix of the string 3 and 4 places. We get a matrix:  5) In the matriarpetrybavim, the third line, multiplied by 5. We obtain a matrix that will have a triangular look:
5) In the matriarpetrybavim, the third line, multiplied by 5. We obtain a matrix that will have a triangular look: 
Systems, their ranks coincide due to rank properties and their rank is Rank Rank
Remarks:1) Unlike the traditional Gauss method, if all the elements are divided into a certain number in the matrix string, we do not have the right to reduce the matrix string by virtue of the properties of the matrix. If we want to reduce the string to a certain number, you will have to cut the entire matrix to this number. 2) In the event that we get a linearly dependent string, we can remove it from our matrix and replace to zero string. Example:
 It is immediately seen that the second line is expressed through the first, if the first is the first to 2. in the thiak case, we can replace the entire second string to zero. We get:
It is immediately seen that the second line is expressed through the first, if the first is the first to 2. in the thiak case, we can replace the entire second string to zero. We get:  As a result, bringing a matrix or to a triangular one, or to a trapezoidal form, where it does not have linearly dependent vectors, all the zero vectors of the matrix and will be the base of the matrix, but their number of rank.
As a result, bringing a matrix or to a triangular one, or to a trapezoidal form, where it does not have linearly dependent vectors, all the zero vectors of the matrix and will be the base of the matrix, but their number of rank.
This is also an example of a system of vectors in the form of a graph: a system is given where, and. The base of this system will obviously be a vector and, since vectors are expressed through them. This system in graphical form will look at:
Elehentarnі shuttering. Systems of the stingy form.
Elementary conversion matrix - These are such conversions of the matrix, as a result of which the equivalence of matrices persists. Thus, elementary transformations do not change the set solutions of a system of linear algebraic equations, which this matrix represents.
Elementary transformations are used in the Gauss method to bring the matrix to triangular or stepped form.
Elementary Row Transformations Called:
In some courses of the linear algebra, the matrix strings are not released into a separate elementary conversion due to the fact that the permutation of any two lines of the matrix can be obtained using the multiplication of any string of the matrix to the constant, and the addition of a different line multiplied by a constant to any string of the matrix.
Similarly are determined elementary column transformations.
Elementary transformations reversible.
The designation indicates that the matrix can be obtained from the elementary transformations (or vice versa).
Definition
Square matrix is \u200b\u200bcalled diagonalIf all its elements standing outside the main diagonal are zero.
Comment. Diagonal elements of the matrix (i.e., elements standing on the main diagonal) can also be zero.
Example

Definition
Scalar A diagonal matrix is \u200b\u200bcalled, in which all diagonal elements are equal to each other.
Comment. If the zero matrix is \u200b\u200bsquare, then it is also scalar.
Example
![]()
Definition
Single matrix A scalar matrix of order is called, the diagonal elements of which are equal to 1.
Comment. To reduce the recording, the order of a single matrix can not be written, then a single matrix is \u200b\u200bsimply indicated.
Example
![]() - single second order matrix.
- single second order matrix.
2.10. Cutting the matrix to diagonal
Normal (in particular symmetric) matrix A. can be brought to the diagonal type by the conversion of similarity -
A. = Tλt −1
Here Λ \u003d Diag (λ 1, ..., λ N.) is a diagonal matrix, the elements of which are the eigenvalues \u200b\u200bof the matrix A., but T. - This is a matrix made up of the corresponding matrix eigenvets A.. T. = (v. 1 ,...,v. N.).
For example,

Fig. 23 Bringing to diagonal form
Step matrix
Definition
Speed called a matrix that satisfies the following conditions:
Definition
Speed It is called a matrix that contains strings and in which the first diagonal elements are nonzero, and the elements underlying the main diagonal and the elements of the last rows are zero, that is, this is a matrix of the form:

Definition
The main element A certain row of the matrix is \u200b\u200bcalled its first nonzero element.
Example
The task. Find the main elements of each row of the matrix ![]()
Decision. The main element of the first line is the first nonzero element of this line, and therefore - the main element of the string at number 1; Similarly, the main element of the second line.
Another definition of a stepped matrix.
Definition
The matrix is \u200b\u200bcalled speed, if a:
all its zero lines are standing after nonzero;
in each nonzero line, starting from the second, its main element is to the right (in a column with a large number) of the main element of the previous line.
By definition to step matrices, we will attract a zero matrix, as well as a matrix that contains one line.
Example
Examples of stepped matrices:
![]() , ,
, ,  ,
,  ,
,
Examples of matrices that are not stepped:
![]() ,
,  ,
, 
Example
The task. Find out whether the matrix is  stepped.
stepped.
Decision. Check the fulfillment of the conditions from the definition:
So, the specified matrix is \u200b\u200ba stepped.
 Error appearance during program launch
Error appearance during program launch FRIGATE plugin for Firefox
FRIGATE plugin for Firefox How to show hidden folders and files in Windows
How to show hidden folders and files in Windows Ways how to make a screen on a laptop brighter or darker
Ways how to make a screen on a laptop brighter or darker How to format a flash drive, disk protection
How to format a flash drive, disk protection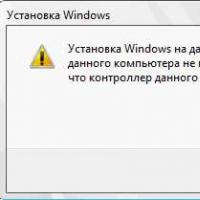 If installing Windows to this disc is not possible
If installing Windows to this disc is not possible During installation of Windows "Make sure that the controller of this disc is included in the computer's BIOS menu.
During installation of Windows "Make sure that the controller of this disc is included in the computer's BIOS menu.