For which the determinant of the matrix is \u200b\u200bneeded. Deterpetes of square matrices. Methods for calculating identifiers
- Release the blue to death!
Let her climbs freedom!
And the ship sails, and the reactor roars ...
- Pasha, did you touch?
I remember class until the 8th I did not like the algebra. At all I did not like. She inflamed me. Because I did not understand anything there.
And then everything has changed, because I am parted one chip:
In mathematics, in general (and algebra in particular), everything is built on a competent and consistent system of definitions. You know definitions, you understand their essence - the rest will not be difficult.
So with the theme of today's lesson. We will consider in detail several related issues and definitions, thanks to which you once and forever understand and with matrices, and with determinants, and with all their properties.
The determinants are a central concept in the algebra of matrices. Like the formulas of abbreviated multiplication, they will chase you throughout the entire course of higher mathematics. Therefore, we read, look and understand thoroughly. :)
And start with the most intimate - and what is the matrix? And how to work with it.
Proper arrangement of indexes in the matrix
The matrix is \u200b\u200bjust a table filled with numbers. Neo here.
One of the key characteristics of the matrix is \u200b\u200bits dimension, i.e. The number of rows and columns from which it consists. It is usually said that a certain $ a $ matrix has a size of $ \\ left [M \\ Times N \\ Right] $, if it has $ m $ rows and $ n $ columns. Record it like this:
Or like this:
There are other designations - everything depends on the preferences of the lecturer / seminarist / author of the textbook. But in any case, with all these $ \\ left] $ and $ ((a) _ (ij)) $ ((a) _ (ij)), the same problem arises:
What index for what is responsible for? First goes the line number, then the column? Or vice versa?
When reading lectures and textbooks, the answer will seem obvious. But when on the exam in front of you - only a leaf with a task, you can pass through and suddenly get confused.
Therefore, let's deal with this question once and forever. To begin with, let us recall the conventional coordinate system from the School Course of Mathematics:
Introduction of the coordinate system on the plane
Remember it? She has the beginning of the coordinate (point $ o \u003d \\ left (0; 0 \\ right) $) an axis of $ x $ and $ y $, and each point on the plane is uniquely determined by coordinates: $ a \u003d \\ left (1; 2 \\ And now let's take this design and put it next to the matrix so that the origin of the coordinate is in the upper left corner. Why there? Yes, because opening a book, we start to read from the left
top corner pages - Remember it is easier than light. But where to send axles? We will direct them so that our entire virtual "page" is covered by these axes. True, for this you have to turn our coordinate system. Only
possible variant this location: Overlaying coordinate system on the matrix
 Now every matrix cell has unambiguous coordinates of $ x $ and $ y $. For example, a record $ ((a) _ (24)) $ means that we appeal to the element with coordinates $ x \u003d 2 $ and $ y \u003d $ 4. The dimensions of the matrix are also definitely set by a pair of numbers:
Now every matrix cell has unambiguous coordinates of $ x $ and $ y $. For example, a record $ ((a) _ (24)) $ means that we appeal to the element with coordinates $ x \u003d 2 $ and $ y \u003d $ 4. The dimensions of the matrix are also definitely set by a pair of numbers: Definition of indexes in the matrix
 Just look at this picture carefully. Play coordinates (especially when you work with real matrices and determinants) - and very soon will understand that even in the most difficult theorems and definitions you understand what we are talking about.
Just look at this picture carefully. Play coordinates (especially when you work with real matrices and determinants) - and very soon will understand that even in the most difficult theorems and definitions you understand what we are talking about. Figured out? Well, go to the first step of enlightenment - the geometric definition of the determinant. :)
Geometric definition
First of all, I would like to note that the determinant exists only for square matrices of the type $ \\ left [N \\ Times N \\ Right] $. The determinant is the number that is read on the defined rules and is one of the characteristics of this matrix (there are other characteristics: rank, own vector, but about it in other lessons).
So what is this characteristic? What does he mean? Everything is simple:
The determinant of the square matrix $ a \u003d \\ left [N \\ Times N \\ Right] $ is the volume of $ n $-dimensional parallelepiped, which is formed if we consider the matrix rows as vectors forming the roof of this parallelepiped.
For example, the determinant of the 2x2 size matrix is \u200b\u200bsimply the area of \u200b\u200bthe parallelogram, and for the 3x3 matrix it is already the volume of 3-dimensional parallelepipeda, which is the same that so infuriates all high school students in the stereometry lessons.
At first glance, this definition may seem completely inadequate. But let's not hurry with conclusions - I look at the examples. In fact, everything is elementary, Watson:
A task. Find the determinants of the matrices:
\\ [\\ left | \\ Begin (Matrix) 1 & 0 \\\\ 0 & 3 \\\\ End (Matrix) \\ Right | \\ quad \\ left | \\ Begin (Matrix) 1 & -1 \\\\ 2 & 2 \\\\ End (Matrix) \\ Right | \\ quad \\ left | \\ Begin (Matrix) 2 & 0 & 0 \\\\ 1 & 3 & 0 \\\\ 1 & 1 & 4 \\\\ End (Matrix) \\ Right | \\]
Decision. The first two determinants are 2x2. So it's just square parallelograms. Having draw them and consider the square.
The first parallelogram is built in vector $ ((V) _ (1)) \u003d \\ left (1; 0 \\ right) $ and $ ((V) _ (2)) \u003d \\ left (0; 3 \\ right) $:
The determinant 2x2 is the area of \u200b\u200bthe parallelogram
Obviously, it is not just a parallelogram, but quite a rectangle. His area is equal
The second parallelogram is built in vector $ ((V) _ (1)) \u003d \\ left (1; -1 \\ right) $ and $ ((V) _ (2)) \u003d \\ left (2; 2 \\ right) $. Well, so what? This is also a rectangle:
Another determinant 2x2
The sides of this rectangle (in fact - the length of the vectors) are easily considered by the Pythagora theorem:
\\ [\\ Begin (Align) & \\ Left | ((v) _ (1)) \\ right | \u003d \\ sqrt ((((1) ^ (2)) + ((\\ left (-1 \\ right)) ^ (2))) \u003d \\ SQRT (2); \\\\ & \\ Left | ((v) _ (2)) \\ right | \u003d \\ sqrt (((2) ^ (2)) + ((2) ^ (2))) \u003d \\ sqrt (8) \u003d 2 \\ SQRT (2); \\\\ & S \u003d \\ Left | ((V) _ (1)) \\ Right | \\ Cdot \\ left | ((v) _ (2)) \\ Right | \u003d \\ SQRT (2) \\ CDot 2 \\ SQRT (2) \u003d 4. \\\\\\ End (Align) \\]
It remains to deal with the latest determinant - there is already a 3x3 matrix. We have to remember stereometer:
The determinant 3x3 is the volume of parallelepiped
It looks brainstorm, but in fact it is enough to remember the formula of the volume of parallelepiped:
where $ s $ is the base area (in our case, this is the area of \u200b\u200bthe parallelogram on the plane of $ oxy $), $ H $ is an height conducted to this base (in essence, $ Z $ -Cordinity $ ((V) _ (3) ) $).
The area of \u200b\u200bthe parallelogram (we ran separately) is also considered easy:
\\ [\\ begin (align) & s \u003d 2 \\ cdot 3 \u003d 6; \\\\ & V \u003d S \\ Cdot H \u003d 6 \\ CDot 4 \u003d 24. \\\\\\ End (Align) \\]
That's all! Record answers.
Answer: 3; four; 24.
A little remark about the designation system. Someone will probably not like that I ignore the "arrows" above the vectors. Allegedly so you can confuse the vector with a point or something else.
But let's seriously: we are already adult boys and girls, so we understand from the context when it comes to the vector, and when - about the point. The arrows only clog the story, and without that tissue stuffed with mathematical formulas.
And further. In principle, nothing interferes with considering and the determinant of the 1x1 matrix - such a matrix is \u200b\u200bsimply one cell, and the number recorded in this cell will be determined. But here there is an important note:
Unlike classical volume, the determinant will give us the so-called " oriented volume", I.e. Volume taking into account the sequence of consideration of row vectors.
And if you want to get the volume in the classical sense of the word, you will have to take the module of the determinant, but now it is not necessary to steam about it - all the same, after a few seconds, we will learn to consider any determinant with any signs, sizes, etc. :)
Algebraic definition
With all the beauty and clarity of the geometric approach, he has a serious disadvantage: he does not tell us anything about how this very determinant is considered.
Therefore, now we will analyze an alternative definition - algebraic. For this, we will need a brief theoretical preparation, but at the output we will get a tool that allows you to read in the matrices as you like.
True, there will appear new problem... But first things first.
Permutations and inversion
Let's drink in a line of numbers from 1 to $ n $. It turns out something like this:
Now (purely on joke) change a couple of numbers in places. You can change the neighboring:
And it is possible - not very neighboring:
And you know what? And nothing! In algebra, this crap is called permutation. And she has a bunch of properties.
Definition. The permutation of the length $ n $ is a string of $ n $ different numbers recorded in any sequence. The first $ n $ natural numbers are usually considered (i.e., just 1, 2, ..., $ n $), and then mix them to obtain the desired permutation.
The permutations are indicated in the same way as the vectors are simply the letter and consistent listing of their elements in brackets. For example: $ p \u003d \\ left (1; 3; 2 \\ Right) $ or $ p \u003d \\ left (2; 5; 1; 4; 3 \\ Right) $. The letter can be any, but let there be $ per $. :)
Further, for simplicity of presentation, we will work with the permutations of length 5 - they are already quite serious for observing any suspicious effects, but not yet so harshs for the rapid brain, as the permutations of length 6 or more. Here are examples of such permutations:
\\ [\\ begin (align) & ((p) _ (1)) \u003d \\ left (1; 2; 3; 4; 5 \\ right) \\\\ \\ ((p) _ (2)) \u003d \\ left (1 ; 3; 2; 5; 4 \\ RIGHT) \\\\ & ((p) _ (3)) \u003d \\ left (5; 4; 3; 2; 1 \\ Right) \\\\\\ End (Align) \\]
Naturally, the permutation of the length $ n $ can be considered as a function that is defined on the set of $ \\ left \\ (1; 2; ...; n \\ right \\) $ and therefore it displays this set for yourself. Returning to the newly recorded permutations of $ ((p) _ (1)) $, $ ((p) _ (2)) $ and $ ((p) _ (3)) $, we can legally write:
\\ [((p) _ (1)) \\ left (1 \\ right) \u003d 1; ((p) _ (2)) \\ left (3 \\ right) \u003d 2; ((p) _ (3)) \\
The number of different permutations of the length $ n $ is always limited and equal to $ n! $ Is an easily proof fact of combinatorics. For example, if we want to write down all the permutations of length 5, we will very much, because there will be such permutations
One of the key characteristics of any permutation is the number of inversions in it.
Definition. Inversion in the permutation of $ p \u003d \\ left (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \\ Right) $ - every couple $ \\ left (((a) _ (i)); ((a) _ (j)) \\ right) $ such that $ i \\ lt j $, but $ ((a) _ (i)) \\ gt ( (a) _ (j)) $. Simply put, inversion is when a greater number is to the left of the smaller (not necessarily neighboring).
We will denote by $ n \\ left (P \\ Right) $ number of inversions in the permutation of $ p $, but be prepared to meet with other designations in different textbooks and from different authors - there are no uniform standards here. The topic of inversions is very extensive, and a separate lesson will be devoted to her. Now our task is to just learn to consider them in real tasks.
For example, we calculate the number of inversions in the permutation of $ p \u003d \\ left (1; 4; 5; 3; 2 \\ Right) $:
\\ [\\ left (4; 3 \\ right); \\ left (4; 2 \\ right); \\ left (5; 3 \\ right); \\ left (5; 2 \\ right); \\ left (3; 2 \\ RIGHT ). \\]
Thus, $ n \\ left (p \\ right) \u003d $ 5. As you can see, nothing terrible in it. I will immediately say: further we will be interested in not so much the number of $ n \\ left (P \\ Right) $, how much is its readiness / oddness. And here we smoothly go to the key term of today's lesson.
What is the determinant
Let a square matrix $ a \u003d \\ left [N \\ Times N \\ Right] $. Then:
Definition. The identifier of the matrix $ a \u003d \\ left] $ is the algebraic amount of $ n! $ Terms compiled as follows. Each term is a product of $ n $ matrix elements taken according to one of each row and each column, multiplied by (-1) to the degree of inversions:
\\ [\\ left | A \\ Right | \u003d \\ Sum \\ Limits_ (n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}
A fundamental point when choosing multipliers for each term in the determinant is the fact that no two factors stand in one line or in one column.
Due to this, it is possible without limiting the generality to assume that the $ i $ index indices ((a) _ (i; j)) $ "run" values \u200b\u200b1, ..., $ n $, and indices $ j $ are some permutation from First:
And when there is a rearrangement of $ p $, we will easily consider the inversion $ n \\ left (P \\ Right) $ - and the next term is ready for the next term.
Naturally, no one forbids to change the places of multipliers in anyone (or in all at once - what are it finally?), And then the first indices will also be some permutation. But in the end, nothing will change: the total number of inversions in the $ I $ and $ J $ indexes retains readiness with such perversions, which is quite consistent with the old-good rule:
From the permutation of multipliers, the number of numbers does not change.
But it is not necessary to check this rule to multiply the matrices - in contrast to multiplication of numbers, it is not commutative. But I'm broken. :)
Matrix 2x2.
In fact, it is possible to consider the 1x1 matrix - it will be one cell, and its determinant, as it is easy to guess, is equal to the number recorded in this cell. Nothing interesting.
Therefore, let's look at a square matrix of 2x2 dimensions:
\\ [\\ left [\\ begin (MATRIX) ((a) _ (11)) & ((a) _ (12)) \\\\ ((a) _ (21)) & ((a) _ (22)) \\\\ End (Matrix) \\ RIGHT] \\]
Since the number of rows in it is $ n \u003d $ 2, the determinant will contain $ n! \u003d 2! \u003d 1 \\ Cdot 2 \u003d $ 2 components. Drink them:
\\ [\\ begin (align) & ((\\ left (-1 \\ right)) ^ (n \\ left (1; 2 \\ right))) \\ Cdot ((a) _ (11)) \\ CDOT ((A) _ (22)) \u003d ((\\ left (-1 \\ right)) ^ (0)) \\ Cdot ((a) _ (11)) \\ Cdot ((a) _ (22)) \u003d ((a) _ (11)) ((a) _ (22)); \\\\ & ((\\ left (-1 \\ right)) ^ (n \\ left (2; 1 \\ right))) \\ cdot ((a) _ (12)) \\ CDOT ((a) _ (21)) \u003d ((\\ left (-1 \\ right)) ^ (1)) \\ Cdot ((a) _ (12)) \\ Cdot ((a) _ (21)) \u003d ((a) _ (12)) ( (a) _ (21)). \\\\\\ End (Align) \\]
Obviously, in the permutation of $ \\ left (1; 2 \\ right) $ consisting of two elements, there are no inversions, therefore $ n \\ left (1; 2 \\ right) \u003d 0 $. But in the permutation of $ \\ left (2; 1 \\ right) $ one inversion is available (actually 2< 1), поэтому $N\left(2;1 \right)=1.$
Total universal formula for calculating the determinant for the 2x2 matrix looks like this:
\\ [\\ left | \\ Begin (Matrix) ((a) _ (11)) & ((a) _ (12)) \\\\ ((a) _ (21)) & ((a) _ (22)) \\\\\\ END ( Matrix) \\ Right | \u003d ((a) _ (11)) ((a) _ (22)) - ((a) _ (12)) ((a) _ (21)) \\]
Graphically, this can be represented as a product of elements standing on the main diagonal, minus the product of elements on a side:
 The determinant of the 2x2 matrix
The determinant of the 2x2 matrix Consider a couple of examples:
\\ [\\ left | \\ Begin (Matrix) 5 & 6 \\\\ 8 & 9 \\\\ End (Matrix) \\ Right |; \\ quad \\ left | \\ Begin (Matrix) 7 & 12 \\\\ 14 & 1 \\\\ End (Matrix) \\ Right |. \\]
Decision. Everything is considered in one line. First matrix:
And the second:
Answer: -3; -161.
However, it was too simple. Let's look at the 3x3 matrices - there is already interesting.
Matrix 3x3
Now consider the square 3x3 size matrix:
\\ [\\ left [\\ begin (Matrix) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\\\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\\\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33) ) \\\\\\ End (Matrix) \\ RIGHT] \\]
When calculating its determinant, we will get $ 3! \u003d 1 \\ CDot 2 \\ CDot 3 \u003d $ 6 terms - not too much for panic, but it's enough to start looking for some patterns. To begin with, we drink all the permutations of three elements and consider inversion in each of them:
\\ [\\ begin (align) & ((p) _ (1)) \u003d \\ left (1; 2; 3 \\ right) \\ rightarrow n \\ left (((p) _ (1)) \\ Right) \u003d n \\ \\\\ & ((p) _ (2)) \u003d \\ left (1; 3; 2 \\ right) \\ rightarrow n \\ left ((((p) _ (2)) \\ right) \u003d n \\ left (1; 3 ; 2 \\ RIGHT) \u003d 1; \\\\ & ((p) _ (3)) \u003d \\ left (2; 1; 3 \\ right) \\ rightarrow n \\ left (((p) _ (3)) \\ right) \u003d n \\ left (2; 1 ; 3 \\ RIGHT) \u003d 1; \\\\ & ((p) _ (4)) \u003d \\ left (2; 3; 1 \\ right) \\ rightarrow n \\ left (((p) _ (4)) \\ right) \u003d n \\ left (2; 3 ; 1 \\ RIGHT) \u003d 2; \\\\ & ((p) _ (5)) \u003d \\ left (3; 1; 2 \\ right) \\ rightarrow n \\ left (((p) _ (5)) \\ right) \u003d n \\ left (3; 1 ; 2 \\ RIGHT) \u003d 2; \\\\ & ((p) _ (6)) \u003d \\ left (3; 2; 1 \\ right) \\ rightarrow n \\ left (((p) _ (6)) \\ Right) \u003d n \\ left (3; 2 ; 1 \\ RIGHT) \u003d 3. \\\\\\ End (Align) \\]
As expected, 6 permutations of $ ((p) _ (1)) $, ... $ ((p) _ (6)) $ ((Naturally, could be written in another sequence - the essence of this is not Changes), and the number of inversions in them varies from 0 to 3.
In general, we will have three terms with the "plus" (where $ n \\ left (P \\ Right) $ is one) and three more with a "minus". In general, the determinant will be considered by the formula:
\\ [\\ left | \\ Begin (Matrix) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\\\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\\\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33)) \\\\\\ END (Matrix) \\ Right | \u003d \\ Begin (Matrix) ((a) _ (11)) ((a) _ (22)) ((a) _ (33)) + ((a) _ (12)) ( (a) _ (23)) ((a) _ (31)) + ((a) _ (13)) ((a) _ (21)) ((a) _ (32)) - \\\\ - ( (a) _ (13)) ((a) _ (22)) ((a) _ (31)) - ((a) _ (12)) ((a) _ (21)) ((a) _ (33)) - ((a) _ (11)) ((a) _ (23)) ((a) _ (32)) \\\\\\ End (Matrix) \\]
That's just not need to sit down and fiercely to sharpen all these indexes! Instead of incomprehensible digits, it is better to remember the following mnemonic rule:
Triangle rule. To find the determinant of the 3x3 matrix, it is necessary to fold three works of elements on the main diagonal and in the vertices of an equally chained triangles with a side parallel to this diagonal, and then subtract the same three works, but on the side diagonal. Schematically, it looks like this:
3x3 matrix determinant: Rule of triangles
It is these triangles (or pentagram - who likes how best) love to draw in all sorts of textbooks and algebra techniques. However, we will not be about sad. Let's better consider one such determinant - for warm-ups before the real tint. :)
A task. Calculate the determinant:
\\ [\\ left | \\ Begin (Matrix) 1 & 2 & 3 \\\\ 4 & 5 & 6 \\\\ 7 & 8 & 1 \\\\ End (Matrix) \\ Right | \\]
Decision. We work according to the rule of triangles. First, consider the three components made up of elements on the main diagonal and in parallel to it:
\\ [\\ Begin (Align) & 1 \\ CDOT 5 \\ CDOT 1 + 2 \\ CDOT 6 \\ CDOT 7 + 3 \\ CDOT 4 \\ CDOT 8 \u003d \\\\ & \u003d 5 + 84 + 96 \u003d 185 \\\\\\ End (Align) \\]
Now we understand with a side diagonal:
\\ [\\ Begin (Align) & 3 \\ CDOT 5 \\ CDOT 7 + 2 \\ CDOT 4 \\ CDOT 1 + 1 \\ CDOT 6 \\ CDOT 8 \u003d \\\\ & \u003d 105 + 8 + 48 \u003d 161 \\\\ End (Align) \\]
It remains only to subtract from the first number of the second - and we will get the answer:
That's all!
However, the determinants of the 3x3 matrices are not the top of the skill. The most interesting is waiting for us further. :)
General scheme for calculating determinants
As we know, with the growth of the dimension of the matrix $ n $ the number of terms in the determinant is $ n! $ And grow rapidly. Still, factorial is that you don't fuck a dog rather fast growing function.
Already for the 4x4 matrices, the determinants are altered (i.e. through the permutations) becomes somehow not very good. About 5x5 and more generally silent. Therefore, some properties of the determinant are connected to the case, but for their understanding, a small theoretical preparation is needed.
Ready? Go!
What is minor matrix
Let an arbitrary matrix $ a \u003d \\ left [M \\ Times N \\ Right] $. Notice: not necessarily square. Unlike determinants, minors are such nyashki that exist not only in harsh square matrices. We choose in this matrix several (for example, $ k $) rows and columns, and the $ 1 \\ le k \\ le m $ and $ 1 \\ le k \\ le n $. Then:
Definition. Minor is about $ k $ - the determinant of the square matrix arising from the intersection of the selected $ k $ columns and rows. Also, I will be called this new matrix itself.
It is indicated by such minor $ ((m) _ (k)) $. Naturally, one matrix may have a whole bunch of minors about $ k $. Here is an example of a minor of order 2 for the $ \\ left matrix [5 \\ Times 6 \\ Right] $:
Choice of $ k \u003d $ 2 columns and rows for minor formation
It is absolutely optional that the selected lines and columns stood near, as in the considered example. The main thing is that the number of selected rows and columns is the same (this is the number $ K $).
There is another definition. Perhaps someone else will like the soul:
Definition. Let the rectangular matrix $ a \u003d \\ left [M \\ Times N \\ Right] $. If, after crossing out one or more columns and one or several rows, a square matrix of the size of $ \\ left [k \\ time k \\ right] $ is formed, then its determinant is a minor $ ((m) _ (k)) $ . We will sometimes call the matrix too, it will be clear from the context.
As my cat spoke, sometimes it is better to crawl once from the 11th floor there is food than meowing, sitting on the balcony.
Example. Let the matrix be given
Choosing a string 1 and column 2, we get minor of the first order:
\\ [((M) _ (1)) \u003d \\ left | 7 \\ RIGHT | \u003d 7 \\]
Choosingrs 2, 3 and columns 3, 4, we get a second-order minor:
\\ [((M) _ (2)) \u003d \\ left | \\ Begin (Matrix) 5 & 3 \\\\ 6 & 1 \\\\ End (Matrix) \\ Right | \u003d 5-18 \u003d -13 \\]
And if you choose all three lines, as well as columns 1, 2, 4, there will be a minor of the third order:
\\ [((M) _ (3)) \u003d \\ left | \\ Begin (Matrix) 1 & 7 & 0 \\\\ 2 & 4 & 3 \\\\ 3 & 0 & 1 \\\\ End (Matrix) \\ Right | \\]
The reader will not be difficult to find other minors of orders of 1, 2 or 3. Therefore, we go further.
Algebraic add-ons
"Well OK, and what do these minions give us minions?" - Surely you ask. By yourself - nothing. But in square matrices, every minor appears "companion" - an additional minor, as well as an algebraic addition. And together, these two ears will allow us to climb the determinants like nuts.
Definition. Let the square matrix $ a \u003d \\ left [N \\ Times N \\ Right] $, in which the minor $ ((m) _ (k)) $ is selected. Then an additional minor for minor $ ((m) _ (k)) $ is a piece of the initial matrix $ A $, which will remain when highlighting all rows and columns involved in the preparation of minor $ ((m) _ (k)) $:
Additional minor to minor $ ((m) _ (2)) $
Specify one moment: an additional minor is not just a "piece of the matrix", but the determinant of this piece.
An additional minors are designated with the help of "Stars": $ M_ (k) ^ (*) $:
where the $ a \\ nabla operation ((m) _ (k)) literally means "delete from $ a $ strings and columns included in $ ((m) _ (k)) $. This operation is not generally accepted in mathematics - I just came up with it for the beauty of the narration. :)
Additional minors are rarely used by themselves. They are part of a more complex design - algebraic supplement.
Definition. Algebraic addition of minor $ ((m) _ (k)) $ is an additional minor $ M_ (k) ^ (*) $ multiplied by $ ((\\ left (-1 \\ right)) ^ (S)) $ where $ s $ is the sum of numbers of all rows and columns involved in the initial minor $ ((m) _ (k)) $.
As a rule, the algebraic addition of minor $ ((m) _ (k)) $ is denoted by $ ((a) _ (k)) $. Therefore:
\\ [((A) _ (k)) \u003d ((\\ left (-1 \\ right)) ^ (s)) \\ Cdot M_ (k) ^ (*) \\]
Complicated? At first glance - yes. But it is not exactly. Because in fact everything is easy. Consider an example:
Example. Dana Matrix 4x4:
Choose a minor of the second order
\\ [((M) _ (2)) \u003d \\ left | \\ Begin (Matrix) 3 & 4 \\\\ 15 & 16 \\\\ End (Matrix) \\ Right | \\]
The captain is obvious as it hints to us that, in the preparation of this minor, strings 1 and 4 were involved, as well as columns 3 and 4. We finish them - we get an additional minor:
It remains to find the number $ s $ and get an algebraic addition. Since we know the numbers of the involved lines (1 and 4) and columns (3 and 4), everything is simple:
\\ [\\ begin (align) & s \u003d 1 + 4 + 3 + 4 \u003d 12; \\\\ & ((a) _ (2)) \u003d ((\\ left (-1 \\ right)) ^ (s)) \\ Cdot M_ (2) ^ (*) \u003d ((\\ Left (-1 \\ RIGHT) ) ^ (12)) \\ Cdot \\ left (-4 \\ right) \u003d - 4 \\ end (align) \\]
Answer: $ ((a) _ (2)) \u003d - $ 4
That's all! In fact, all the difference between an additional minor and an algebraic addition - only in the minus front, and it is not always.
Laplas Theorem
And so we came to what, in fact, all these minors and algebraic additions were needed.
Laplace Theorem on the decomposition of the determinant. Let $ k $ of strings (columns), and $ 1 \\ le k \\ le n-1 $, are selected in the $ \\ left [N \\ Times N \\ Right] $. Then the determinant of this matrix is \u200b\u200bequal to the sum of all the works of minors of the order of $ k $ contained in the selected lines (columns), on their algebraic additions:
\\ [\\ left | A \\ right | \u003d \\ sum (((m) _ (k)) \\ cdot ((a) _ (k))) \\]
Moreover, such terms will be exactly $ C_ (n) ^ (k) $.
Okay, okay: about $ c_ (n) ^ (k) $ - this is me already in the original Laplace theorem there was nothing like that. But nobody canceled the combinatorics, and literally a quick look at the condition will allow you to make it yourself to make sure that the components will be so much. :)
We will not prove it, even though it does not represent much difficulties - all the calculations are reduced to old-kind permutations and readiness / oddness of inversions. Nevertheless, the proof will be presented in a separate paragraph, and today we have a purely practical lesson.
Therefore, we turn to a private case of this theorem when minors are individual matrix cells.
Decomposition of the string and column
What now let's spell about - just there is a basic tool for working with determinants, for which all this game was inhabited with permutations, miners and algebraic additions.
Read and enjoy:
Consequence of the Laplace Theorem (decomposition of a string / column). Let one line be selected in the Matrix of the $ \\ left] $ of [N \\ Times N \\ Right] $. Miners in this line will be $ n $ individual cells:
\\ [((M) _ (1)) \u003d ((a) _ (ij)), \\ quad j \u003d 1, ..., n \\]
Additional minors are also easily considered: just take the original matrix and highlight the string and column containing $ ((a) _ (ij)) $. We will call such minors $ m_ (ij) ^ (*) $.
For an algebraic supplement, the number of $ s $ is still needed, but in the case of Minor about 1, it is simply the sum of the "coordinate" of the cell $ ((a) _ (ij)) $:
And then the original determinant can be written through $ ((a) _ (ij)) $ and $ m_ (ij) ^ (*) $ according to the Laplace Theorem:
\\ [\\ left | A \\ Right | \u003d \\ Sum \\ Limits_ (j \u003d 1) ^ (n) (((a) _ (ij)) \\ CDOT ((\\ left (-1 \\ right)) ^ (i + j)) \\ CDOT ((M) _ (ij))) \\]
That's what it is decomposition formula for string. But the same is true for columns.
From this consequence, you can immediately formulate several conclusions:
- This scheme works equally well for both rows and columns. In fact, the discontinuity will most often go on columns than on rows.
- The number of terms in the decomposition is always exactly $ n $. This is significantly less than $ c_ (n) ^ (k) $ and even more than $ n! $.
- Instead of one determinant $ \\ left [N \\ Times N \\ Right] $, you will have to consider several size determinants per unit less: $ \\ left [\\ left (N-1 \\ Right) \\ Times \\ Left (N-1 \\ Right) \\ Right ] $.
The last fact is especially important. For example, instead of a brutal determinant, 4x4 now it will be enough to calculate several determinants of 3x3 - we can cope with them. :)
A task. Find the determinant:
\\ [\\ left | \\ Begin (Matrix) 1 & 2 & 3 \\\\ 4 & 5 & 6 \\\\ 7 & 8 & 9 \\\\ End (Matrix) \\ Right | \\]
Decision. We will decompose this determinant on the first line:
\\ [\\ Begin (Align) \\ Left | A \\ Right | \u003d 1 \\ CDOT ((\\ left (-1 \\ right)) ^ (1 + 1)) \\ CDOT \\ Left | \\ Begin (Matrix) 5 & 6 \\\\ 8 & 9 \\\\ End (Matrix) \\ Right | + \\\\ 2 \\ Cdot ((\\ Left (-1 \\ Right)) ^ (1 + 2)) \\ CDOT \\ left | \\ Begin (Matrix) 4 & 6 \\\\ 7 & 9 \\\\ End (Matrix) \\ Right | + \\\\ 3 \\ CDOT ((\\ Left (-1 \\ Right)) ^ (1 + 3)) \\ CDOT \\ left | \\ Begin (Matrix) 4 & 5 \\\\ 7 & 8 \\\\ End (Matrix) \\ Right | \u003d & \\\\\\ End (Align) \\]
\\ [\\ Begin (Align) & \u003d 1 \\ Cdot \\ left (45-48 \\ Right) -2 \\ CDOT \\ LEFT (36-42 \\ RIGHT) +3 \\ CDOT \\ LEFT (32-35 \\ RIGHT) \u003d \\\\ \\\\\\ End (Align) \\]
A task. Find the determinant:
\\ [\\ left | \\ Begin (Matrix) 0 & 1 & 1 & 0 \\\\ 1 & 0 & 1 & 1 \\\\ 1 & 1 & 0 & 1 \\\\ 1 & 1 & 1 & 0 \\\\ End (Matrix) \\ Right | \\
Decision. For a diversity, let's work with columns this time. For example, two zero are present in the last column - obviously, it will significantly reduce the calculation. Now you will see why.
So, we declare the determinant for the fourth column:
\\ [\\ Begin (Align) \\ Left | \\ Begin (Matrix) 0 & 1 & 1 & 0 \\\\ 1 & 0 & 1 & 1 \\\\ 1 & 1 & 0 & 1 \\\\ 1 & 1 & 1 & 0 \\\\ End (Matrix) \\ Right | \u003d 0 \\ CDOT ((\\ Left (-1 \\ Right)) ^ (1 + 4)) \\ Cdot \\ Left | \\ Begin (Matrix) 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\ 1 & 1 & 1 \\\\ End (Matrix) \\ Right | + \\\\ +1 \\ CDOT ((\\ Left (-1 \\ \\ Begin (Matrix) 0 & 1 & 1 \\\\ 1 & 1 & 0 \\\\ 1 & 1 & 1 \\\\ End (Matrix) \\ Right | + & \\\\ +1 \\ Cdot ((\\ Left (-1 \\ \\ Begin (Matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 1 \\\\ End (Matrix) \\ Right | + \\\\0 \\ CDOT ((\\ Left (-1 \\ \\ Begin (Matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\ End (Matrix) \\ Right | \\\\\\ End (Align) \\]
And here - oh, miracle! - The two components immediately fly to the cat under the tail, since they have a "0" multiplier. There are two more determinants of the 3x3, with which we will easily figure out:
\\ [\\ Begin (Align) & \\ Left | \\ Begin (Matrix) 0 & 1 & 1 \\\\ 1 & 1 & 0 \\\\ 1 & 1 & 1 \\\\ End (Matrix) \\ Right | \u003d 0 + 0 + 1-1-1-0 \u003d -1; \\\\ & \\ Left | \\ Begin (Matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 1 \\\\ End (Matrix) \\ Right | \u003d 0 + 1 + 1-0-0-1 \u003d 1. \\\\\\ End (Align) \\]
We return to the source and find the answer:
\\ [\\ left | \\ Begin (Matrix) 0 & 1 & 1 & 0 \\\\ 1 & 0 & 1 & 1 \\\\ 1 & 1 & 0 & 1 \\\\ 1 & 1 & 1 & 0 \\\\ End (Matrix) \\ Right | \u003d 1 \\ CDOT \\ LEFT (-1 \\ RIGHT) + \\ LEFT (-1 \\ RIGHT) \\ CDOT 1 \u003d -2 \\]
That's it. And no 4! \u003d 24 terms did not have to be considered. :)
Answer: -2.
The main properties of the determinant
In the last task, we saw how the presence of zeros in the strings (columns) of the matrix sharply simplifies the decomposition of the determinant and in general all the calculations. The natural question arises: whether it is impossible to make that these zeros appear even in that matrix where they were originally not?
The answer is unequivocal: can. And here we assist the properties of the determinant:
- If you change two lines (column) in places, the determinant will not change;
- If one line (column) is multiplied by the number $ k $, then the entire determinant will also multiply by the number $ k $;
- If you take one line and add (subtract) it how much time from another one, the determinant will not change;
- If the two lines of the determinant are the same, either proportional or one of the rows is filled with zeros, then the entire determinant is zero;
- All the above properties are true for columns.
- When transposing the matrix, the determinant does not change;
- The determinant of the work of the matrices is equal to the product of the determinants.
Of particular value is the third property: we can remove from one line (column) the other until zeros appear in the right places.
Most often, the calculations are reduced to "reset" the entire column everywhere, except for one element, and then decompose the determinant for this column, having received a matrix of 1 less matrix.
Let's see how it works in practice:
A task. Find the determinant:
\\ [\\ left | \\ Begin (Matrix) 1 & 2 & 3 & 4 \\\\ 4 & 1 & 2 & 3 \\\\ 3 & 3 & 4 & 1 & 2 \\\\ 2 & 3 & 4 & 1 \\\\ End (Matrix) \\ Right | \\ Decision. Zeros here, as it were, not observed at all, so you can "drop" on any row or column - the volume of calculations will be approximately the same. Let's not finish and "reset" the first column: there is already a cell with a unit in it, so we simply take the first line and subtract it 4 times from the second, 3 times from the third and 2 times from the last one.
As a result, we get a new matrix, but its determinant will be the same:
\\ [\\ Begin (Matrix) \\ left | \\ Begin (Matrix) 1 & 2 & 3 & 4 \\\\ 4 & 1 & 2 & 3 \\\\ 3 & 3 & 4 & 1 & 2 \\\\ 2 & 3 & 4 & 1 \\\\ End (Matrix) \\ Right | \\ \\ Begin (Matrix) 1 & 2 & 3 & 4 \\\\ 4-4 \\ CDOT 1 & 1-4 \\ CDOT 2 & 2-4 \\ CDOT 3 & 3-4 \\ CDOT 4 \\\\ 3-3 \\ CDOT 1 & 4-3 \\ CDOT 2 & 1-3 \\ CDOT 3 & 2-3 \\ CDOT 4 \\\\ 2-2 \\ CDOT 1 & 3-2 \\ CDOT 2 & 4-2 \\ CDOT 3 & 1-2 \\ CDOT 4 \\ \\ Begin (Matrix) 1 & 2 & 3 & 4 \\\\ 0 & -7 & -10 & -8 & -10 \\\\ 0 & -1 & -10 \\\\ 0 & -1 & -2 & -7 \\\\ \\\\\\ End (Matrix) \\]
Now with non-vulnerable patch launch this determinant on the first column:
\\ [\\ Begin (Matrix) 1 \\ CDOT ((\\ Left (-1 \\ Right)) ^ (1 + 1)) \\ Cdot \\ Left | \\ Begin (Matrix) -7 & -10 & -13 \\\\ -2 & -8 & -10 \\\\ -1 & -2 & -7 \\\\ -1 End (Matrix) \\ Right | +0 \\ Cdot ((\\ ... \\ Right | + \\\\0 \\ Cdot ((\\ left (-1 \\ right)) ^ (3 + 1)) \\ CDot \\ Left | ... \\ Right | +0 \\ Cdot ((\\ left (-1 \\ right)) ^ (4 + 1)) \\ Cdot \\ left | ... \\ Right | \\\\\\ End (Matrix) \\]
It is clear that "surviving" only the first term - in the rest I didn't even write out the determinants, because they still multiply on zero. The coefficient in front of the determinant is equal to one, i.e. It can not write it.
But you can make "minuses" of all three rows of the determinant. In essence, we made a multiplier three times (-1):
\\ [\\ left | \\ Begin (Matrix) -7 & -10 & -13 \\\\ -2 & -8 & -10 \\\\ -1 -1 & -2 & -7 \\\\ End (Matrix) \\ Right | \u003d \\ CDOT \\ LEFT | \\ Begin (Matrix) 7 & 10 & 13 \\\\ 2 & 8 & 10 \\\\ 1 & 2 & 7 \\\\ End (Matrix) \\ Right | \\]
We received a small determinant 3x3, which can already be calculated according to the rule of triangles. But we will try to decompose it and on the first column - the benefit in the last line is proudly the unit is:
\\ [\\ Begin (Align) & \\ Left (-1 \\ Right) \\ Cdot \\ Left | \\ Begin (Matrix) 7 & 10 & 13 \\\\ 2 & 8 & 10 \\\\ 1 & 2 & 7 \\\\ End (Matrix) \\ Right | \\ Begin (Matrix) -7 \\\\ -2 \\\\ \\ Uparrow \\ \\ Begin (Matrix) 0 & -4 & -36 \\\\ 0 & 4 & -4 \\\\ 1 & 2 & 7 \\\\ End (Matrix) \\ Right | \u003d \\\\ \\ \u003d \\ Cdot \\ left | \\ Begin (Matrix) -4 & -36 \\\\ 4 & -4 \\\\\\ End (Matrix) \\ Right | \u003d \\ Left (-1 \\ Right) \\ Cdot \\ Left | \\ Begin (Matrix) -4 & -36 \\\\ 4 & -4 \\\\\\ End (Matrix) \\ Right | \\\\\\ End (Align) \\]
You can, of course, can still be painted and decompose the 2x2 matrix on the line (column), but we are adequate to you, so we just consider the answer:
\\ [\\ Left (-1 \\ Right) \\ CDOT \\ Left | \\ Begin (Matrix) -4 & -36 \\\\ 4 & -4 \\\\\\ End (Matrix) \\ Right | \u003d \\ Left (-1 \\ Right) \\ Cdot \\ left (16 + 144 \\ RIGHT) \u003d - 160 \\ This is how dreams are broken. Just -160 in response. :)
Answer: -160.
A couple of comments before we turn to the last task:
The initial matrix was symmetrical relative to the side diagonal. All minors in decomposition are also symmetrical about the same side diagonal.
- Strictly speaking, we could not put anything at all, but simply bring the matrix to the ultra-deductive form when there are solid zeros under the main diagonal. Then (in exact accordance with the geometric interpretation, by the way) the determinant is equal to the product $ ((a) _ (ii)) $ - numbers on the main diagonal.
- \\ [\\ left | \\ Begin (Matrix) 1 & 1 & 1 & 1 \\\\ 3 & 4 & 8 & 16 \\\\ 3 & 9 & 27 & 81 \\\\ 5 & 25 & 125 & 625 \\\\\\ End (Matrix) \\ Right | \\ Decision. Well, here the first line is straightforwarded by "zeroing". Take the first column and deduct exactly once from all others:
A task. Find the determinant:
\\ [\\ Begin (Align) & \\ Left | \\ Begin (Matrix) 1 & 1 & 1 & 1 \\\\ 2 & 4 & 8 & 16 \\\\ 3 & 9 & 125 & 81 \\\\ 5 & 25 & 125 & 625 \\\\\\ End (Matrix) \\ Right | \u003d \\\\ & \u003d \\ left | \\ Begin (Matrix) 1 & 1-1 & 1-1 & 1-1 \\\\ 2 & 4-2 & 8-2 & 16-2 \\\\ 3 & 9-3 & 27-3 & 81-3 \\\\ \\ Begin (Matrix) 1 & 0 & 0 & 0 \\\\ 2 & 2 & 6 & 14 \\\\ 3 & 6 & 24 & 78 \\\\ 5 & 20 & 120 & 620 \\\\\\ End (Matrix) \\ Right | \\\\\\ End (Align) \\]
Unlock on the first line, and then we endure common factories from the remaining lines:
\\ [\\ Cdot \\ Left | \\ Begin (Matrix) 2 & 6 & 14 \\\\ 6 & 24 & 78 \\\\ 20 & 120 & 620 \\\\\\ End (Matrix) \\ Right | \u003d \\ Cdot \\ left | \\ Begin (Matrix) 1 & 3 & 7 \\\\ 1 & 4 & 13 \\\\ 1 & 6 & 31 \\\\ End (Matrix) \\ Right | \\]
Over again, we observe the "beautiful" numbers, but in the first column - we declare the determinant on it:
\\ [\\ Begin (Align) & 240 \\ Cdot \\ Left | \\ Begin (Matrix) 1 & 3 & 7 \\\\ 1 & 4 & 13 \\\\ 1 & 6 & 31 \\\\ End (Matrix) \\ Right | \\ Begin (Matrix) \\ Downarrow \\\\ -1 \\\\ -1 \\ \\ Begin (Matrix) 1 & 3 & 7 \\\\ 0 & 1 & 6 \\\\ 0 & 3 & 24 \\\\ End (Matrix) \\ Right | \u003d \\\\ \\ \u003d 240 \\ CDOT ((\\ LEFT (-1 \\ \\ Begin (Matrix) 1 & 6 \\\\ 3 & 24 \\\\ End (Matrix) \\ Right | \u003d \\\\ & \u003d 240 \\ CDOT 1 \\ CDOT \\ LEFT (24-18 \\ RIGHT) \u003d 1440 \\\\\\ END ( align) \\]
Order. The task is solved.
Answer: 1440.
Deterpetes and their properties. Permutation Numbers 1, 2, ..., N is called any arrangement of these numbers in a certain order. In elementary algebra, it is proved that the number of all permutations that can be formed from n numbers is 12 ... n \u003d n!. For example, of three numbers 1, 2, 3, you can form 3! \u003d 6 permutations: 123, 132, 312, 321, 231, 213. It is said that in this permutation of the number I and J constitute inversion (mess), if i\u003e j, but I stand in this permutation earlier than j, that is, if more than the leftmost less.
The permutation is called even (or odd)If in it, accordingly, even (odd) the total number of inversions. The operation by which from one permutation is moving to another composed of the same N numbers, called Forceed nth degree.
The substitution that translates one permutation to another is written by two rows in common brackets, and the numbers occupying the same places in the permutations under consideration are called corresponding And one beneath one is written. For example, the symbol denotes a substitution in which 3 goes to 4, 1 → 2, 2 → 1, 4 → 3. The substitution is called even (or odd) if the total number of inversions in both rows of substitution is even (odd). Any substitution of N-essential can be recorded in the form, i.e. With a natural arrangement of numbers in the top row.
Let us give a square matrix of order n
Consider all possible works for n elements of this matrix taken one by one and only one of each line and each column, i.e. Works of the form:
![]() , (4.4)
, (4.4)
where the indices q 1, q 2, ..., q n make up some permutation from numbers
1, 2, ..., n. The number of such works is equal to the number of different permutations from N characters, i.e. Equally n!. The mark of the work (4.4) is equal to (- 1) q, where Q is the number of inversions in the rearrangement of the second element indices.
Determinant N-order, the corresponding matrix (4.3), is called the algebraic amount n! members of the form (4.4). A symbol is used to record the determinant  or Deta \u003d.
or Deta \u003d.  (determine, or determinant, matrix a).
(determine, or determinant, matrix a).
Properties of determinants
1. The determinant does not change during transposition.
2. If one of the rows of the determinant consists of zeros, then the determinant is zero.
3. If the determinant rearrange two lines, the determinant will change the sign.
4. The determinant containing two identical lines is zero.
5. If all the elements of some string of the determinant are multiplied by a number k, then the determinant itself multiplies on K.
6. The determinant containing two proportional lines is zero.
7. If all items i-th row The determinant is presented as the sum of the two terms A I j \u003d b j + C j (j \u003d 1, ..., n), then the determinant is equal to the amount of determinants, in which all lines besides i-oh, are the same as in the specified definite, and i-I line In one of the components consists of elements B j, in the other - from the elements C j.
8. The determinant does not change if the corresponding elements of another line are added to the elements of one of its rows multiplied by the same number.
Comment. All properties remain valid if instead of rows take columns.
MinorM i J element A I J determined D N-th order is called the determinant of the order of N-1, which is obtained from D crossing the string and column containing this item.
Algebraic supplement The element A i J determined D is called its minor M I J, taken with a sign (-1) i + j. Algebraic addition of the element A i j will be denoted by a i j. Thus, a i j \u003d (-1) i + j m i j.
Methods of practical calculation of determinants based on the fact that the procedure n may be expressed through the determinants of lower orders, gives the following theorem.
Theorem (Determination of the determinant on a string or column).
The determinant is equal to the amount of the works of all elements of the arbitrary line (or column) on their algebraic additions. In other words, there is a decomposition D by i-th elements strings
d \u003d a i 1 a i 1 + a i 2 a i 2 + ... + a i n a i n (i \u003d 1, ..., n)
or jar column
d \u003d a 1 j a 1 j + a 2 j a 2 j + ... + a n j a n j (j \u003d 1, ..., n).
In particular, if all elements of the string (or column), except for one, are zero, then the determinant is equal to this element multiplied by its algebraic addition.
The formula for calculating the third order determinant.


To facilitate memorization of this formula:


Example 2.4.Without calculating the determinant, show that it is zero.
Decision.The first will be subtracted from the second line, we obtain the determinant equal to the original one. If the third line also deduct the first one, then the determinant will be proportional to the two lines. Such a determinant is zero.
Example 2.5.Calculate the determinant d \u003d, decomposing it by elements of the second column.
Decision.We will decompose the determinant for the elements of the second column:
D \u003d A 12 A 12 + A 22 A 22 + A 32 A 32 \u003d
 .
.

Example 2.6. Calculate the determinant
 ,
,
in which all elements on one side of the main diagonal are zero.
Decision.Spatize the determinant A on the first line:
 .
.
The determinant, standing on the right, can be decomposed again on the first line, then we get:
 .
.
Example 2.7. Calculate the determinant  .
.
Decision.If each row of the determinant, starting with the second, add the first line, will result in a determinant in which all the elements below the main diagonal will be zero. Namely, we get the determinant:  equal to the source.
equal to the source.
Arguing, as in the previous example, we find that it is equal to the product of the elements of the main diagonal, i.e. N!. The method by which this determinant is calculated is called the way to bring to the triangular form.
Often, the university includes tasks of higher mathematics, in which it is necessary calculate the determinant of the matrix. By the way, the determinant can only be in square matrices. Below will look at the main definitions, which properties have a determinant and how to calculate it correctly .. Also on the examples, we show a detailed solution.
What is the determinant of the matrix: calculating the determinant using the definition
The determinant of the matrix
The second order is the number.
The determinant of the matrix is \u200b\u200bdenoted - (abbreviated from the Latin name determinants), or.
If: then it turns out
Recall a few more auxiliary definitions:
Definition
An ordered set of numbers that consists of elements is called the permutation of order.
For a set that contains elements there is a factorial (N), which is always indicated exclamation familiar:. The permutations differ from each other only by the order of the following. To make it clearer, give an example:
Consider a variety of three elements (3, 6, 7). Total permutations 6, since.:
Definition
Inversion in the permutation of order is an ordered set of numbers (it is also called in bijection), where of them two numbers form a confusion. It is when more of the numbers in this permutation is located to the left of a smaller number.
Above, we considered an example with a permutation inversion, where there were numbers. So, take the second line, where the judging by these numbers it turns out that, and, since the second element is greater than the third element. Take for comparison the sixth string, where numbers are located :. There are three couples here:, and since Title \u003d "(! Lang: Rendered by QuickTex.com" height="13" width="42" style="vertical-align: 0px;">; , так как title="Rendered by QuickLatex.com." height="13" width="42" style="vertical-align: 0px;">; , – title="Rendered by QuickLatex.com." height="12" width="43" style="vertical-align: 0px;">.!}
We will not study the inversion itself, but the permutations will be very useful to us in the future considering the topic.
Definition
Determined Matrix X - Number:
- rearrangement of numbers from 1 to an infinite number, and - the number of inversions in the permutation. Thus, the determinant includes terms, which are called "member of the determinant".
It is possible to calculate the determinant of the second order matrix, the third and even fourth. It is also worth mentioning:
Definition
the determinant of the matrix is \u200b\u200ba number that is equal
To understand this formula, we describe it in more detail. The determinant of the square matrix X is the amount that contains the terms, and each term is a product of a certain number of matrix elements. At the same time, in each work there is an element from each row and each column of the matrix.
Before a certain term, it may appear if the elements of the matrix in the work go in order (by line number), and the number of inversions in the permutation of the set of columns are odd.
It was mentioned above that the determinant of the matrix is \u200b\u200bdenoted or, that is, the determinant is often called determinant.
So, back to the formula:
From the formula, it is clear that the determinant of the first order matrix is \u200b\u200ban element of the same matrix.
Calculation of the determinant of the second order matrix
Most often in practice, the matrix determinant is solved by the methods of the second, third and less frequently, the fourth order. Consider how the determinant of the second order matrix is \u200b\u200bcalculated:
In the second order matrix, it follows that factorial. Before applying the formula
It is necessary to determine which data we turn out:
2. Rearrangements: and;
3. The number of inversions in the permutation: and, since Title \u003d "(! Lang: Rendered by QuickTex.com" height="13" width="42" style="vertical-align: -1px;">;!}
4. Relevant works: and.
It turns out:
Based on the foregoing, we get a formula for calculating the determinant of the second order square matrix, that is, x:
Consider on specific exampleHow to calculate the second order square matrix determinant:
Example
A task
Calculate the determinant of the X matrix:
Decision
So, we turn out ,,,.
To solve, it is necessary to take advantage of the previously considered formula:
We substitute the number from the example and find:
Answer
The determinant of the second order matrix \u003d.
Calculation of the third-order matrix determinant: an example and solution by the formula
Definition
The third-order matrix determinant is the number obtained from nine given numbers located in the form of a square table,
The third order determinant is almost the same as the second order determinant. The difference is only in the formula. Therefore, if you well navigate in the formula, then there will be no problems with the solution.
Consider a third-order square matrix *:
Based on this matrix, we understand that, accordingly, factorial \u003d, which means that the entire permutation is obtained
To apply the formula correctly, you need to find data:
So, the total permutations of the set:
The number of inversions in the permutation, and the corresponding works \u003d;
Number of inversions in the permutation title \u003d "(! Lang: Rendered by QuickTex.com" height="18" width="65" style="vertical-align: -4px;">, соответствующие произведения = ;!}
Inversions in the permutation of title \u003d "(! Lang: Rendered by QuickTex.com" height="18" width="65" style="vertical-align: -4px;"> ;!}
. ; Inversions in the permutation of title \u003d "(! Lang: Rendered by QuickTex.com" height="18" width="118" style="vertical-align: -4px;">, соответствующие произведение = !}
. ; Inversions in the permutation of title \u003d "(! Lang: Rendered by QuickTex.com" height="18" width="118" style="vertical-align: -4px;">, соответствующие произведение = !}
. ; Inversions in the permutation of title \u003d "(! Lang: Rendered by QuickTex.com" height="18" width="171" style="vertical-align: -4px;">, соответствующие произведение = .!}
Now we have:
Thus, we obtained the formula for calculating the determinant of the matrix of order x:
Finding the third order matrix according to the rule of the triangle (Sarrusus rule)
As mentioned above, the elements of the 3rd order determinant are located in three rows and three columns. If you enter the designation of the general element, then the first element indicates the line number, and the second element from the indexes is the column number. There is home (elements) and side (elements) diagonal of the determinant. The components in the right part are called the members of the determinant).
It can be seen that each member of the determinant is in the scheme only one element in each row and each column.
You can calculate the determinant using a rectangle rule, which is depicted in the form of a schema. Red-based members of the determinant from the elements of the main diagonal, as well as members from the elements that are in the top of the triangles, are on one side, parallel to the main diagonal (levy scheme), take a sign.
Members with blue arrows from cell diagonal elements, as well as from elements that are in the vertices of triangles, which have parties parallel to the side diagonal (right scheme) are taken with a sign.

The following example will learn how to calculate the third-order square matrix determinant.
Example
A task
Calculate the third order matrix determinant:
Decision
In this example:
Calculate the determinant using the formula or scheme, which were considered above:
Answer
The determinant of the third order matrix \u003d
The main properties of the third-order matrix determinants
Based on previous definitions and formulas, consider the main properties of the determinant of the matrix.
1. The size of the determinant will not change when replacing the corresponding rows, columns (such a replacement is called transpose).
On the example, it is convinced that the determinant of the matrix is \u200b\u200bequal to the determinant of the transposed matrix:
Recall the formula for calculating the determinant:
We transform the matrix:
Calculate the determinant of the transposed matrix:
We made sure that the determinant of the transported matrix is \u200b\u200bequal to the original matrix, which indicates the right solution.
2. The identifier sign will change to the opposite if it is switched in places any two columns or two lines.
Consider on the example:
Two third-order matrices (X) are given:
It is necessary to show that these matrices are opposite.
Decision
In the matrix and the matrix changed lines (third from the first, and from the first to third). According to the second property, the determinants of two matrices should be different. That is, one matrix with a positive sign, and the second one is negative. Let's check this property by applying the formula to calculate the determinant.
The property is true, since.
3. The determinant is zero, if there are the same corresponding elements in two lines (columns). Let the identifier be the same elements of the first and second columns:
Changing the same columns in places, we, according to the property 2, we obtain a new determinant: \u003d. On the other hand, the new determinant coincides with the original, since the same responses elements, that is \u003d. From these equations, we turn out: \u003d.
4. The determinant is zero if all the elements of the same row (column) zeros. This statement floates from the fact that each member of the determinant in the formula (1) is one, and only one element from each line (column), which has some zeros.
Consider on the example:
We show that the determinant of the matrix is \u200b\u200bzero:
In our matrix there are two identical columns (second and third), therefore, based on this propertyThe determinant should be zero. Check:
And indeed, the determinant of the matrix with two identical columns is zero.
5. The total multiplier of the elements of the first string (column) can be reached for the identifier sign:
6. If the elements of one row or one column of the determinant are proportional to the corresponding elements of the second line (column), then such a determinant is zero.
Indeed, for the property of 5, the ratio of proportionality can be made for the sign of the determinant, and then take advantage of the property 3.
7. If each of the elements of the string (columns) of the determinant is the sum of the two terms, this determinant can be submitted as the sum of the respective determinants:
To check, it is enough to write down in the deployment of the software (1) the determinant that in the left part of equality, then separately group members in which items are contained and objects from the obtained groups of terms will be the first and second determinant with the right part of equality.
8. The definition values \u200b\u200bwill not change if the corresponding elements of the second line (column) multiplied with the same number are added to the element of a string or one column:
This equality is obtained based on properties 6 and 7.
9. The determinant of the matrix ,, equals the amount of works of elements of any row or column on their algebraic additions.
Here the software implies an algebraic addition of the matrix element. Using this property, you can calculate not only the matrix of the third order, but also the matrices of more higher orders (x or x). Forward words are a recurrent formula that is needed in order to calculate the determinant of the matrix of any order. Remember it, as it is often used in practice.
It is worth saying that with the help of the ninth property, you can calculate the determinants of the matrices of not only the fourth order, but also more of the higher orders. However, it is necessary to make a lot of computing operations and be attentive, since the slightest error in signs will lead to an incorrect decision. Matrices of higher orders are most convenient to solve the Gauss method, and talk about it later.
10. The determinant of the work of the matrices of one order is equal to the product of their determinants.
Consider on the example:
Example
A task
Make sure that the determinant of two matrices is equal to the product of their determinants. Two matrices are given:
Decision
First we find the product of the determinants of two matrices and.
Now we will perform multiplication of both matrices and thus we calculate the determinant:
Answer
We made sure that
Calculation of the determinant of the matrix using the Gauss method
The determinant of the matrix Updated: November 22, 2019 by the author: Scientific articles.ru.
You can put in line with some numbercalculated by a specific rule and called determinant.
The need to introduce a concept determinant - numbersCharacterized square order matrix n. , closely related to solving systems of linear algebraic equations.
The determinant of the matrix BUT We will denote: | BUT| or D.
Determinant of the first order matrixBUT = (but 11) called an element but eleven . For example, for BUT \u003d (-4) We have | BUT| = -4.
Second order matrix determinantcalled numberdefined by the formula
|BUT| = .
For example, | BUT| =  .
.
 |
 |
 |
||
Words this rule can be written as: with his sign you need to take the product of the elements connected main diagonal, and the works of elements connected by the vertices of triangles, whose base parallel to the main diagonal. With reverse sign, similar works are taken, only relative to the side diagonal.
For example,
Determination of the determinant of the matrix n.- It will not be ordered, but we will show the method of finding it.
In the future, instead of words the determinant of the matrix n.order We will say simple determinant n.order. We introduce new concepts.
Let a square matrix be given n.-o order.
MinorM. IJ element but IJ matrix BUTcalled determinant (n.-1) -go order obtained from the matrix BUT Hacking out i.Line I. j.-to column.
Algebraic addition A IJ element A IJ matrix A is called His Minor, taken with a sign (-1) i + J:
BUT ij \u003d (-1) i + j M. IJ,
those. An algebraic addition or coincides with its minor, when the sum of the lines and column numbers - an even number, or differs from it, when the sum of the line numbers and column is an odd number.
For example, for elements but 11 I. but 12 matrix A \u003d.  Minora
Minora
M. 11 = BUT 11 =  ,
,
M. 12 =  ,
,
but BUT 12 = (-1) 1+2 M. 12 = -8.
Theorem (on the decomposition of the determinant) . The determinant of the square matrix is \u200b\u200bequal to the amount of the works of the elements of any row (column) on their algebraic additions, i.e.
|BUT| = but I1 A. i1 +. but I2. A. I2 + ... + but IN. A. in,
for anyone i. = 1, 2, …, n.
|BUT| = but 1J. A. 1J +. but 2J. A. 2J + ... + but NJ. A. NJ,
for anyone j. = 1, 2, …, n.
The first formula is called i.lines, And the second - decomposition of the determinant for elements j.-to column.
It is not difficult to understand that with the help of these formulas any determinant n.-o order can be reduced to the amount of determinants whose order will be 1 less, etc. So far, do not reach the determinants of the 3rd or 2nd orders, the calculation of which no longer represents difficulties.
To find the determinant, the following main properties can be applied:
1. If some string (or column) of the determinant consists of zeros, then the determinant itself is zero.
2. When permuting any two lines (or two columns), the determinant is multiplied by -1.
3. The determinant with two identical or proportional lines (or columns) is zero.
4. The general factor of the elements of any row (or column) can be made for the sign of the determinant.
5. The value of the determinant will not change if all the rows and columns are swapped.
6. The value of the determinant will not change if one of the rows (or to one of the columns) add another string (column) multiplied by any number.
7. The amount of the works of elements of some line (or column) of the matrix to algebraic supplements of the elements of another string (column) of this matrix is \u200b\u200bzero.
8. The determinant of the work of two square matrices is equal to the product of their determinants.
The introduction of the concept of the matrix determinant allows you to determine another action with matrices - finding the reverse matrix.
For each non-zero number there is an opposite number, such that the product of these numbers gives a unit. For square matrices, there is also such a concept.
The matrix BUT -1 called inversetowards square Matrix BUTif with multiplying this matrix on this on both on the right and the left is obtained single matrix.
BUT× BUT -1 = BUT -1 × BUT= E.
From the definition it follows that only the square matrix has a reverse; In this case, the reverse matrix will be the square of the same order. However, not every square matrix has its own reverse.
In the general case, the calculation rule of the identifiers $ n $ -to order is quite bulky. For determinants of the second and third order, there are rational methods for their calculations.
Calculations of second-order determinants
To calculate the determinant of the matrix of the second order, it is necessary to take the work of elements of the side diagonal from the product of the elements of the main diagonal:
$$ \\ left | \\ begin (array) (LL) (A_ (11)) & (A_ (12)) \\\\ (A_ (21)) & (A_ (22)) \\ END (Array) \\ Right | \u003d A_ (11) \\ Example
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ END (Array) \\ Right | \u003d 11 \\ CDOT 5 - (- 2) \\ CDOT 7 \u003d 55 + 14 \u003d 69 $
Decision. Answer.
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69 Methods for calculating third-order determinants
For calculating third-order determinants, there are such rules.
Triangle rule
Schematically this rule can be depicted as follows:
The product of the elements in the first determinant, which are connected by straight, is taken with a "plus" sign; Similarly, for the second determinant - the corresponding works are taken with the "minus" sign, i.e.

$$ \\ left | \\ Begin (Array) (CCC) (A_ (11)) & (A_ (12)) & (A_ (13)) \\\\ (A_ (21)) & (A_ (22)) & (A_ (23)) \\\\ (A_ (31)) & (A_ (32)) & (A_ (33)) \\ END (Array) \\ Right | \u003d A_ (11) A_ (22) A_ (33) + A_ (12) A_ ( 23) A_ (31) + A_ (13) A_ (21) A_ (32) - $$
$$ - A_ (11) A_ (23) A_ (32) -A_ (12) A_ (21) A_ (33) -A_ (13) A_ (22) A_ (31) $$
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Calculate the identifier $ \\ left | \\ Begin (Array) (RRR) (3) & (3) & (-1) \\\\ (4) & (1) & (3) \\\\ (1) & (-2) & (-2) \\ END (Array) \\ Right | $ by triangles.
Decision. $ \\ left | \\ Begin (Array) (RRR) (3) & (3) & (-1) \\\\ (4) & (1) & (3) \\\\ (1) & (-2) & (-2) \\ END (Array) \\ Right | \u003d 3 \\ CDOT 1 \\ CDOT (-2) +4 \\ Cdot (-2) \\ CDOT (-1) + $
$$ + 3 \\ CDOT 3 \\ CDOT 1 - (- 1) \\ CDOT 1 \\ CDOT 1-3 \\ CDOT (-2) \\ CDOT 3-4 \\ CDOT 3 \\ CDOT (-2) \u003d 54 $$
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69
Sarrus rule
To the right of the determinant add the first two columns and the works of elements on the main diagonal and on diagonals, parallel to it, they take a plus sign; And the works of elements of the side diagonal and diagonals, to it parallel, with the "minus" sign:

$$ - A_ (13) A_ (22) A_ (31) -A_ (11) A_ (23) A_ (32) -A_ (12) A_ (21) A_ (33) $$
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Calculate the identifier $ \\ left | \\ Begin (Array) (RRR) (3) & (3) & (-1) \\\\ (4) & (1) & (3) \\\\ (1) & (-2) & (-2) \\ END (Array) \\ Right | $ Using the Sarryus rule.
Decision. 
$$ + (- 1) \\ CDOT 4 \\ CDOT (-2) - (- 1) \\ CDOT 1 \\ CDOT 1-3 \\ CDOT 3 \\ CDOT (-2) -3 \\ CDOT 4 \\ CDOT (-2) \u003d 54 $$.
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69 $ \\ left | \\ Begin (Array) (RRR) (3) & (3) & (-1) \\\\ (4) & (1) & (3) \\\\ (1) & (-2) & (-2) \\ END (Array) \\ Right | \u003d $ 54
Decomposition of the string or column
The determinant is equal to the amount of product elements of the determinant on their algebraic supplements. Usually choose the string / column, in which there is zeros. A string or column for which / wow decomposition is conducted, will be denoted by an arrow.
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Declaring on the first line, calculate the determinant $ \\ left | \\ Begin (Array) (LLL) (1) & (2) & (3) \\\\ (4) & (5) & (6) \\\\ (7) & (8) & (9) \\ END (Array) \\ Right | $
Decision. $ \\ left | \\ Begin (Array) (LLL) (1) & (2) & (3) \\\\ (4) & (5) & (6) \\\\ (7) & (8) & (9) \\ END (Array) \\ Right | \\ leftarrow \u003d a_ (11) \\ Cdot A_ (11) + A_ (12) \\ Cdot A_ (12) + A_ (13) \\ CDot A_ (13) \u003d $
$ 1 \\ Cdot (-1) ^ (1 + 1) \\ Cdot \\ Left | \\ Begin (Array) (CC) (5) & (6) \\\\ (8) & (9) \\ END (Array) \\ Right | +2 \\ Cdot (-1) ^ (1 + 2) \\ Cdot \\ Left | \\ Begin (Array) (CC) (4) & (6) \\\\ (7) & (9) \\ END (Array) \\ Right | +3 \\ Cdot (-1) ^ (1 + 3) \\ Cdot \\ Left | \\ Begin (Array) (CC) (4) & (5) \\ (7) & (8) \\ END (Array) \\ Right | \u003d -3 + 12-9 \u003d 0 $
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69
This method allows the calculation of the determinant to be reduced to the calculation of the determinant of a lower order.
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Calculate the identifier $ \\ left | \\ Begin (Array) (LLL) (1) & (2) & (3) \\\\ (4) & (5) & (6) \\\\ (7) & (8) & (9) \\ END (Array) \\ Right | $
Decision. We will perform the following transformations above the stakes of the determinant: from the second line, take four first, and from the third first line multiplied by seven, as a result, according to the properties of the determinant, we obtain the determinant equal to this.
$$ \\ left | \\ Begin (Array) (CCC) (1) & (2) & (3) \\\\ (4) & (5) & (6) \\\\ (7) & (8) & (9) \\ END (Array) \\ Right | \u003d \\ left | \\ Begin (Array) (CCC) (1) & (2) & (3) \\\\ (4-4 \\ CDOT 1) & (5-4 \\ CDOT 2) & (6-4 \\ CDOT 3) \\\\ ( 7-7 \\ CDOT 1) & (8-7 \\ CDOT 2) & (9-7 \\ CDOT 3) \\ END (Array) \\ Right | \u003d $$
$$ \u003d \\ left | \\ Begin (Array) (RRR) (1) & (2) & (3) \\\\ (0) & (-3) & (-6) \\\\ (0) & (-6) & (-12) \\ \\ Begin (Array) (CCC) (1) & (2) & (3) \\\\ (0) & (-3) & (-6) \\\\ (0) & (2 \\ Cdot (-3)) & (2 \\ Cdot (-6)) \\ END (Array) \\ Right | \u003d 0 $$
The determinant is zero, since the second and third lines are proportional.
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69 $ \\ left | \\ Begin (Array) (LLL) (1) & (2) & (3) \\\\ (4) & (5) & (6) \\\\ (7) & (8) & (9) \\ END (Array) \\ RIGHT | \u003d 0 $
To calculate the fourth-order determinants and above, either decomposition on a string / column, or bringing to a triangular form, or using the Laplace Theorem.
Decomposition of the determinant on elements of a string or column
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Calculate the identifier $ \\ left | \\ Begin (Array) (LLLL) (9) & (8) & (7) & (6) \\\\ (5) & (4) & (3) & (2) \\\\ (1) & (0) & (1) & (2) \\\\ (3) & (4) & (5) & (6) \\ END (Array) \\ Right | $, settling it on some row elements or some column.
Decision. Pre-execute the elementary conversion over the rows of the determinant, making as much zeros as possible either in the string or in the column. To do this, at first from the first line, we take away nine-thirds, from the second - five thirds and from the fourth - three third lines, we get:
$$ \\ left | \\ Begin (Array) (CCCC) (9) & (8) & (7) & (6) \\\\ (5) & (4) & (3) & (2) \\\\ (1) & (0) & (1) & (2) \\\\ (3) & (4) & (5) & (6) \\ END (Array) \\ Right | \u003d \\ left | \\ Begin (Array) (CCCC) (9-1) & (8-0) & (7-9) & (6-18) \\\\ (5-5) & (4-0) & (3-5) & (2-10) \\\\ (1) & (0) & (1) & (2) \\\\ (0) & (4) & (2) & (0) \\ END (Array) \\ Right | \u003d \\ \\ Begin (Array) (RRRR) (0) & (8) & (-2) & (-12) \\\\ (0) & (4) & (-2) & (-8) \\\\ (1) & (0) & (1) & (2) \\\\ (0) & (4) & (2) & (0) \\ End (Array) \\ Right | $$
The resulting determinant will be decomposed on the elements of the first column:
$$ \\ left | \\ Begin (Array) (RRRR) (0) & (8) & (-2) & (-12) \\\\ (0) & (4) & (-2) & (-8) \\\\ (1) & (0) & (1) & (2) \\\\ (0) & (4) & (2) & (0) \\ END (Array) \\ Right | \u003d 0 + 0 + 1 \\ Cdot (-1) ^ ( 3 + 1) \\ Cdot \\ Left | \\ Begin (Array) (RRR) (8) & (-2) & (-12) \\\\ (4) & (-2) & (-8) \\\\ (4) & (2) & (0) \\
The resulting third-order determinant also decompose on the elements of the string and column, previously obtained zeros, for example, in the first column. For this, from the first line, we take two second lines from the first line, and from the third - the second:
$$ \\ left | \\ Begin (Array) (RRR) (8) & (-2) & (-12) \\\\ (4) & (-2) & (-8) \\\\ (4) & (2) & (0) \\ \\ Begin (Array) (RRR) (0) & (2) & (4) \\\\ (4) & (-2) & (-8) \\\\ (0) & (4) & (8) \\ END ( Array) \\ Right | \u003d 4 \\ Cdot (-1) ^ (2 + 2) \\ Cdot \\ left | \\ Begin (Array) (LL) (2) & (4) \\\\ (4) & (8) \\ End (Array) \\ Right | \u003d $$
$$ \u003d 4 \\ CDOT (2 \\ CDOT 8-4 \\ CDOT 4) \u003d 0 $$
$ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | \u003d $ 69 $ \\ left | \\ Begin (Array) (CCCC) (9) & (8) & (7) & (6) \\\\ (5) & (4) & (3) & (2) \\\\ (1) & (0) & (1) & (2) \\\\ (3) & (4) & (5) & (6) \\ END (Array) \\ Right | \u003d 0 $
Comment
The latter and penultimate determinants could not be calculated, but to immediately conclude that they are zero, as they contain proportional lines.
Determine the determinant for triangular
Via elementary transformations Above lines or columns, the determinant is driven to a triangular form and then its value, according to the properties of the determinant, is equal to the product of elements on the main diagonal.
The task.
Calculate the second order determinant $ \\ left | \\ Begin (Array) (RR) (11) & (-2) \\\\ (7) & (5) \\ End (Array) \\ Right | $ Calculate the identifier $ \\ delta \u003d \\ left | \\ Begin (Array) (RRRR) (- 2) & (1) & (3) & (2) \\\\ (3) & (0) & (-1) & (2) \\\\ (-5) & ( 2) & (3) & (0) \\\\ (4) & (-1) & (2) & (-3) \\ End (Array) \\ Right | $ bringing it to a triangular form.
Decision. First we make zeros in the first column under the main diagonal. All transformations will be easier if the $ element $ (11) $ is equal to 1. To do this, we will change the first and second columns of the determinant, which, according to the properties of the determinant, will lead to what it will change the sign to the opposite:
$$ \\ Delta \u003d \\ left | \\ Begin (Array) (RRRR) (- 2) & (1) & (3) & (2) \\\\ (3) & (0) & (-1) & (2) \\\\ (-5) & ( 2) & (3) & (0) \\\\ (4) & (-1) & (2) & (-3) \\ END (Array) \\ Right | \u003d - \\ Left | \\ Begin (Array) (RRRR) (1) & (-2) & (3) & (2) \\\\ (0) & (3) & (-1) & (2) \\\\ (2) & (- 5) & (3) & (0) \\\\ (-1) & (4) & (2) & (-3) \\ END (Array) \\ Right | $$
$$ \\ Delta \u003d - \\ Left | \\ Begin (Array) (RRRR) (1) & (-2) & (3) & (2) \\\\ (0) & (3) & (-1) & (2) \\\\ (0) & (- 1) & (-3) & (-4) \\\\ (0) & (2) & (5) & (-1) \\ End (Array) \\ Right | $$
Next, we get zeros in the second column on the site of elements under the main diagonal. And again, if the diagonal element is equal to $ \\ pm $ 1, then the calculations will be simpler. For this, we change the second and third lines in places (and at the same time changes to the opposite sign of the determinant):
$$ \\ Delta \u003d \\ left | \\ Begin (Array) (RRRR) (1) & (-2) & (3) & (2) \\\\ (0) & (-1) & (-3) & (-4) \\\\ (0) & (3) & (-1) & (2) \\\\ (0) & (2) & (5) & (-1) \\ END (Array) \\ Right | $$
 Cellular - what it is on the iPad and what's the difference
Cellular - what it is on the iPad and what's the difference Go to digital television: What to do and how to prepare?
Go to digital television: What to do and how to prepare? Social polls work on the Internet
Social polls work on the Internet Savin recorded a video message to the Tyuments
Savin recorded a video message to the Tyuments Menu of Soviet tables What was the name of Thursday in Soviet canteens
Menu of Soviet tables What was the name of Thursday in Soviet canteens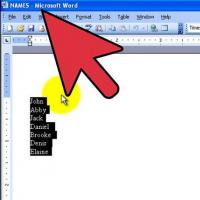 How to make in the "Word" list alphabetically: useful tips
How to make in the "Word" list alphabetically: useful tips How to see classmates who retired from friends?
How to see classmates who retired from friends?