Приведення до ступінчастому увазі з рішенням. Приведення матриці до ступінчастого вигляду. Елементарні перетворення рядків і стовпців. Критерій лінійної залежності векторів
Щоб привести матрицю до ступінчастого вигляду (рис. 1.4), потрібно виконати наступні дії.
1. У першому стовпці вибрати елемент, відмінний від нуля ( провідний елемент ). Рядок з провідним елементом ( провідна рядок ), Якщо вона не перша, переставити на місце першого рядка (перетворення I типу). Якщо в першому стовпці немає ведучого (всі елементи дорівнюють нулю), то виключаємо цей стовпець, і продовжуємо пошук провідного елементу в решти матриці. Перетворення закінчуються, якщо виключені всі стовпці або в частині матриці всі елементи нульові.
2. Розділити всі елементи провідного рядка на провідний елемент (перетворення II типу). Якщо провідна рядок остання, то на цьому перетворення слід закінчити.
3. До кожної рядку, розташованої нижче провідною, додати провідний рядок, помножену відповідно на таке число, щоб елементи, які стоять під провідним виявилися рівними нулю (перетворення III типу).
4. Виключивши з розгляду рядок і стовпець, на перетині яких стоїть провідний елемент, перейти до пункту 1, в якому всі описані дії застосовуються до решти матриці.
7. Теорема про розклад візначніка по елементів рядка.
Теорема про розкладання визначника за елементами рядка або стовпця дозволяє звести обчислення визначника - го порядку () до обчислення визначників порядку .
Якщо визначник має рівні нулю елементи, то зручніше за все розкладати визначник за елементами тієї рядки або стовпці, який містить найбільшу кількість нулів.
Використовуючи властивості визначників, можна перетворити визначник - го порядку так, щоб всі елементи деякого рядка або стовпця, крім одного, стали рівними нулю. Таким чином, обчислення визначника - го порядку, якщо він відмінний від нуля, зведеться до обчислення одного визначника - го порядку.
Завдання 3.1.обчислити визначник
Рішення. Додавши до другої рядку першу, до третьої - першу, помножену на 2, до четвертої - першу, помножену на -5, отримаємо
Розкладаючи визначник за елементами першого стовпчика, маємо
В отриманому визначнику 3-го порядку звернемо в нуль всі елементи першого стовпчика, крім першого. Для цього до другої рядку додамо першу, помножену на (-1), до третьої, помноженої на 5, додамо першу, помножену на 8. Так як множили третій рядок на 5, то (для того, щоб визначник не змінився) помножимо його на . маємо
Отриманий визначник розкладемо за елементами першого стовпця:
8. Теорема Лапласа (1). Теорема про чужі ДОПОВНЕННЯ (2)
1) Определітельравенсуммепроізведеній елементів якого-небудь рядка на іхалгебраіческіедополненія.
2) Суммапроізведенійелементовкакой-якого рядка визначника на алгебраїчні доповнення відповідних елементів іншого його рядки дорівнює нулю (теорема про примноження на чужі алгебраїчні доповнення).
9. Аріфметічні векторні простори.
Будь-яка точка на площині при вибраній системі координат задається парою (α, β) своїх координат; числа α і β можна розуміти також як координати радіуса-вектора з кінцем в цій точці. Аналогічно, в просторі трійка (α, β, γ) визначає точку або вектор з координатами α, β, γ. Саме на цьому грунтується добре відома читачеві геометрична інтерпретація систем лінійних рівнянь з двома або трьома невідомими. Так, в разі системи двох лінійних рівнянь з двома невідомими
а 1 х + b 1 у \u003d с 1,
а 2 х + b 2 у \u003d з 2
кожне з рівнянь тлумачиться як пряма на площині (див. рис. 26), а рішення (α, β) - як точка перетину цих прямих або як вектор з координатами аїр (рисунок відповідає випадку, коли система має єдине рішення).
Мал. 26
Аналогічно можна вчинити з системою лінійних рівнянь з трьома невідомими, інтерпретуючи кожне рівняння як рівняння площини в просторі.
В математиці і різних її додатках (зокрема, в теорії кодування) доводиться мати справу з системами лінійних рівнянь, що містять більше трьох невідомих. Системою лінійних рівнянь з n невідомими x 1, х 2, ..., х n називається сукупність рівнянь виду
а 11 х 1 + а 12 х 2 + ... + а 1n х n \u003d b 1,
а 21 х 1 + а 22 х 2 + ... + а 2n х n \u003d b 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
а m1 х 1 + а m2 х 2 + ... + а mn х n \u003d b m,
де a ij і b i - довільні дійсні числа. Число рівнянь в системі може бути будь-яким і ніяк не пов'язане з числом невідомих. Коефіцієнти при невідомих а ij мають подвійну нумерацію: перший індекс i вказує номер рівняння, другий індекс j - номер невідомого, при якому варто даний коефіцієнт. Будь-яке рішення системи розуміється як набір (дійсних) значень невідомих (α 1, α 2, ..., α n), що звертають кожне рівняння в правильну рівність.
Хоча безпосереднє геометричне тлумачення системи (1) при n\u003e 3 вже неможливо, однак цілком можливо і в багатьох відносинах зручно поширити на випадок довільного n геометричний мову простору двох або трьох вимірів. Цій меті і служать подальші визначення.
Всякий упорядкований набір з n дійсних чисел (α 1, α 2, ..., α n) називається n-мірним арифметичним вектором, а самі числа α 1, α 2, ..., α n - координатами цього вектора.
Для позначення векторів використовується, як правило, жирний шрифт і для вектора а з координатами α 1, α 2, ..., α n зберігається звичайна форма записи:
а \u003d (α 1, α 2, ..., α n).
За аналогією зі звичайною площиною безліч всіх n-мірних векторів, що задовольняють лінійним рівнянням з n невідомими, називають гиперплоскостью в n-вимірному просторі. При такому визначенні безліч всіх рішень системи (1) є не що інше, як перетин кількох гіперплоскостей.
Додавання і множення n-мірних векторів визначаються за тими ж правилами, що і для звичайних векторів. А саме, якщо
а \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Два n-мірних вектора, то їх сумою називається вектор
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
Твором вектора а на число λ називається вектор
λа \u003d (λα 1, λα 2, ..., λα n). (4)
Безліч всіх n-мірних арифметичних векторів з операціями додавання векторів і множення вектора на число називається арифметичним n-мірним векторних простором L n.
Використовуючи введені операції, можна розглядати довільні лінійні комбінації декількох векторів, т. Е. Вирази виду
λ 1 a 1 + λ 2 a 2 + ... + λ k a k,
де λ i - дійсні числа. Наприклад, лінійна комбінація векторів (2) з коефіцієнтами λ і μ - це вектор
λа + μb \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
У тривимірному просторі векторів особливу роль відіграє трійка векторів i, j, k (координатні орти), за якими розкладається будь-який вектор а:
a \u003d xi + yj + zk,
де х, у, z - дійсні числа (координати вектора а).
В n-вимірному випадку таку ж роль відіграє наступна система векторів:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Всякий вектор а є, очевидно, лінійна комбінація векторів е 1, e 2, ..., e n:
а \u003d а 1 е 1 + а 2 е 2 + ... + а n е n, (6)
причому коефіцієнти α 1, α 2, ..., α n збігаються з координатами вектора а.
Позначаючи через 0 вектор, всі координати якого дорівнюють нулю (коротко, нульовий вектор), введемо наступну важливу визначення:
Система векторів а 1, а 2, ..., а k називається лінійно залежною, якщо існує рівна нульового вектору лінійна комбінація
λ 1 a 1 + λ 2 a 2 + ... + λ k a k \u003d 0,
в якій хоча б один з коефіцієнтів h 1, λ 2, ..., λ k різниться від нуля. В іншому випадку система називається лінійно незалежною.
Так, вектори
а 1 \u003d (1, 0, 1, 1), а 2 \u003d (1, 2, 1, 1), а 3 \u003d (2, 2, 2, 2)
лінійно залежні, оскільки
a 1 + a 2 - а 3 \u003d 0.
Лінійна залежність, як видно з визначення, рівносильна (при k ≥ 2) того, що хоча б один з векторів системи є лінійною комбінацією інших.
Якщо система складається з двох векторів a 1, а 2, то лінійна залежність системи означає, що один з векторів пропорційний іншому, скажімо, а 1 \u003d λа 2; в тривимірному випадку це рівносильно коллинеарности векторів а 1 і а 2. Точно так же лінійна залежність системи I з трьох векторів в звичайному просторі означає компланарність цих векторів. поняття лінійної залежності є, таким чином, природним узагальненням понять коллинеарности і компланарності.
Неважко переконатися, що вектори е 1, е 2, ..., е n з системи (5) лінійно незалежні. Отже, в n-вимірному просторі існують системи з n лінійно незалежних векторів. Можна показати, що будь-яка система з більшого числа векторів лінійно залежна.
Будь-яка система a 1, а 2, ..., а n з n лінійно незалежних векторів n-мірного простору L n називається його базисом.
Будь-вектор а простору L n розкладається, і до того ж єдиним чином, по векторах довільного базису a 1, а 2, ..., а n:
а \u003d λ 1 a 1 + λ 2 a 2 + ... + λ n a n.
Цей факт легко встановлюється на підставі визначення базису.
Продовжуючи аналогію з тривимірним простором, можна і в n-вимірному випадку визначити скалярний твір а · b векторів, вважаючи
a · b \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
При такому визначенні зберігаються всі основні властивості скалярного твори тривимірних векторів. Вектори а і b називаються ортогональними, якщо їх скалярний добуток дорівнює нулю:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
В теорії лінійних кодів використовується ще одне важливе поняття - поняття підпростору. Підмножина V простору L n називається подпространством цього простору, якщо
1) для будь-яких векторів а, b, що належать V, їх сума а + b також належить V;
2) для будь-якого вектора а, що належить V, і для будь-якого дійсного числа λ вектор λа також належить V.
Наприклад, безліч всіх лінійних комбінацій векторів e 1, е 2 з системи (5) буде подпространством простору L n.
У лінійної алгебрі доводиться, що у всякому підпросторі V існує така лінійно незалежна система векторів a 1, a 2, ..., a k, що всякий вектор а підпростору є лінійною комбінацією цих векторів:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ k a k.
Зазначена система векторів називається базисом підпростору V.
З визначення простору і підпростори безпосередньо випливає, що простір L n є комутативна група щодо операції додавання векторів, а будь-яке його підпростір V є підгрупою цієї групи. У цьому сенсі можна, наприклад, розглядати суміжні класи простору L n по подпространству V.
На закінчення підкреслимо, що якщо в теорії n-мірного арифметичного простору замість дійсних чисел (т. Е. Елементів поля дійсних чисел) розглядати елементи довільного поля F, то все визначення і факти, наведені вище, зберегли б силу.
В теорії кодування важливу роль відіграє випадок, коли поле F поле відрахувань Z p, яке, як ми знаємо, звичайно. В цьому випадку відповідне n-мірний простір також звичайно і містить, як неважко бачити, р n елементів.
Поняття простору, як і поняття групи і кільця, допускає також і аксіоматичне визначення. За подробицями ми відсилаємо живильник до будь-якого курсу лінійної алгебри.
10. Лінійна комбінація. Лінійно залежні та незалежні системи векторів.
У даній темі розглянемо поняття матриці, а також види матриць. Так як в даній темі чимало термінів, то я додам короткий зміст, Щоб орієнтуватися в матеріалі було простіше.
Визначення матриці і її елемента. Позначення.
матриця - це таблиця з $ m $ рядків і $ n $ стовпців. Елементами матриці можуть бути об'єкти абсолютно різноманітної природи: числа, змінні або, наприклад, інші матриці. Наприклад, матриця $ \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $ містить 3 рядки і 2 колонки; елементами її є цілі числа. Матриця $ \\ left (\\ begin (array) (cccc) a & a ^ 9 + 2 & 9 & \\ sin x \\\\ -9 & 3t ^ 2-4 & ut & 8 \\ end (array) \\ right) $ містить 2 рядки і 4 шпальти.
Різні способи запису матриць: показати \\ приховати
Матриця може бути записана не тільки в круглих, а й в квадратних або подвійних прямих дужках. Нижче вказана одна і та ж матриця в різних формах запису:
$$ \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right); \\; \\; \\ Left [\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right]; \\; \\; \\ Left \\ Vert \\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right \\ Vert $$
Твір $ m \\ times n $ називають розміром матриці. Наприклад, якщо матриця містить 5 рядків і 3 стовпці, то говорять про матрицю розміру $ 5 \\ times 3 $. Матриця $ \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $ має $ 3 \\ times 2 $.
Зазвичай матриці позначаються великими літерами латинського алфавіту: $ A $, $ B $, $ C $ і так далі. Наприклад, $ B \u003d \\ left (\\ begin (array) (ccc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $. Нумерація рядків йде зверху вниз; стовпців - зліва направо. Наприклад, перший рядок матриці $ B $ містить елементи 5 і 3, а другий стовпець містить елементи 3, -87, 0.
Елементи матриць зазвичай позначаються маленькими літерами. Наприклад, елементи матриці $ A $ позначаються $ a_ (ij) $. Подвійний індекс $ ij $ містить інформацію про становище елемента в матриці. Число $ i $ - це номер рядка, а число $ j $ - номер стовпця, на перетині яких знаходиться елемент $ a_ (ij) $. Наприклад, на перетині другого рядка і п'ятого стовпчика матриці $ A \u003d \\ left (\\ begin (array) (cccccc) 51 & 37 & -9 & 0 & 9 & 97 \\\\ 1 & 2 & 3 & 41 & 59 & 6 \\ 59 $:
Точно так же на перетині першого рядка та першого стовпчика маємо елемент $ a_ (11) \u003d 51 $; на перетині третього рядка і другого шпальти - елемент $ a_ (32) \u003d - 15 $ і так далі. Зауважу, що запис $ a_ (32) $ читається як "а три два", але не "а тридцять два".
Для скороченого позначення матриці $ A $, розмір якої дорівнює $ m \\ times n $, використовується запис $ A_ (m \\ times n) $. Нерідко використовується і такий запис:
$$ A_ (m \\ times (n)) \u003d (a_ (ij)) $$
Тут $ (a_ (ij)) $ вказує на позначення елементів матриці $ A $, тобто говорить про те, що елементи матриці $ A $ позначаються як $ a_ (ij) $. У розгорнутому вигляді матрицю $ A_ (m \\ times n) \u003d (a_ (ij)) $ можна записати так:
$$ A_ (m \\ times n) \u003d \\ left (\\ begin (array) (cccc) a_ (11) & a_ (12) & \\ ldots & a_ (1n) \\\\ a_ (21) & a_ (22) & \\ ldots & a_ (2n) \\\\ \\ ldots & \\ ldots & \\ ldots & \\ ldots \\\\ a_ (m1) & a_ (m2) & \\ ldots & a_ (mn) \\ end (array) \\ right) $$
Введемо ще один термін - рівні матриці.
Дві матриці однакового розміру $ A_ (m \\ times n) \u003d (a_ (ij)) $ і $ B_ (m \\ times n) \u003d (b_ (ij)) $ називаються рівними, Якщо їх відповідні елементи рівні, тобто $ A_ (ij) \u003d b_ (ij) $ для всіх $ i \u003d \\ overline (1, m) $ і $ j \u003d \\ overline (1, n) $.
Пояснення до запису $ i \u003d \\ overline (1, m) $: показати \\ приховати
Запис "$ i \u003d \\ overline (1, m) $" означає, що параметр $ i $ змінюється від 1 до m. Наприклад, запис $ i \u003d \\ overline (1,5) $ говорить про те, що параметр $ i $ приймає значення 1, 2, 3, 4, 5.
Отже, для рівності матриць слід дотримуватися двох умов: збіг розмірів і рівність відповідних елементів. Наприклад, матриця $ A \u003d \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $ не дорівнює матриці $ B \u003d \\ left (\\ 2 $. Також матриця $ A $ не дорівнює матриці $ C \u003d \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 98 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $, оскільки $ a_ ( 21) \\ neq c_ (21) $ (тобто $ 0 \\ neq 98 $). А ось для матриці $ F \u003d \\ left (\\ begin (array) (cc) 5 & 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ end (array) \\ right) $ можна сміливо записати $ A \u003d F $ оскільки і розміри, і відповідні елементи матриць $ A $ і $ F $ збігаються.
приклад №1
Визначити розмір матриці $ A \u003d \\ left (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\\\ -6 & 8 & 23 \\\\ 11 & -12 & -5 \\ Вказати, чому дорівнюють елементи $ a_ (12) $, $ a_ (33) $, $ a_ (43) $.
Дана матриця містить 5 рядків і 3 стовпці, тому розмір її $ 5 \\ times 3 $. Для цієї матриці можна використовувати також позначення $ A_ (5 \\ times 3) $.
Елемент $ a_ (12) $ знаходиться на перетині першого рядка та другого стовпця, тому $ a_ (12) \u003d - 2 $. Елемент $ a_ (33) $ знаходиться на перетині третього рядка і третього стовпця, тому $ a_ (33) \u003d 23 $. Елемент $ a_ (43) $ знаходиться на перетині четвертого рядка і третього стовпця, тому $ a_ (43) \u003d - 5 $.
відповідь: $ A_ (12) \u003d - 2 $, $ a_ (33) \u003d 23 $, $ a_ (43) \u003d - 5 $.
Види матриць в залежності від їх розміру. Головна і побічна діагоналі. Слід матриці.
Нехай задана деяка матриця $ A_ (m \\ times n) $. Якщо $ m \u003d 1 $ (матриця складається з одного рядка), то задану матрицю називають матриця-рядок. Якщо ж $ n \u003d 1 $ (матриця складається з одного стовпця), то таку матрицю називають матриця-стовпець. Наприклад, $ \\ left (\\ begin (array) (ccccc) -1 & -2 & 0 & -9 & 8 \\ end (array) \\ right) $ - матриця-рядок, а $ \\ left (\\ begin (array) (c) -1 \\\\ 5 \\\\ 6 \\ end (array) \\ right) $ - матриця-стовпець.
Якщо для матриці $ A_ (m \\ times n) $ вірно умова $ m \\ neq n $ (тобто кількість рядків не дорівнює кількості стовпців), то часто говорять, що $ A $ - прямокутна матриця. Наприклад, матриця $ \\ left (\\ begin (array) (cccc) -1 & -2 & 0 & 9 \\\\ 5 & 9 & 5 & 1 \\ end (array) \\ right) $ має $ 2 \\ times 4 $, тобто містить 2 рядки і 4 шпальти. Так як кількість рядків не дорівнює кількості стовпців, то ця матриця є прямокутної.
Якщо для матриці $ A_ (m \\ times n) $ вірно умова $ m \u003d n $ (тобто кількість рядків дорівнює кількості стовпців), то говорять, що $ A $ - квадратна матриця порядку $ n $. Наприклад, $ \\ left (\\ begin (array) (cc) -1 & -2 \\\\ 5 & 9 \\ end (array) \\ right) $ - квадратна матриця другого порядку; $ \\ Left (\\ begin (array) (ccc) -1 & -2 & 9 \\\\ 5 & 9 & 8 \\\\ 1 & 0 & 4 \\ end (array) \\ right) $ - квадратна матриця третього порядку. В загалом вигляді квадратну матрицю $ A_ (n \\ times n) $ можна записати так:
$$ A_ (n \\ times n) \u003d \\ left (\\ begin (array) (cccc) a_ (11) & a_ (12) & \\ ldots & a_ (1n) \\\\ a_ (21) & a_ (22) & \\ ldots & a_ (2n) \\\\ \\ ldots & \\ ldots & \\ ldots & \\ ldots \\\\ a_ (n1) & a_ (n2) & \\ ldots & a_ (nn) \\ end (array) \\ right) $$
Кажуть, що елементи $ a_ (11) $, $ a_ (22) $, $ \\ ldots $, $ a_ (nn) $ знаходяться на головній діагоналі матриці $ A_ (n \\ times n) $. Ці елементи називаються головними діагональними елементами (Або просто діагональними елементами). Елементи $ a_ (1n) $, $ a_ (2 \\; n1) $, $ \\ ldots $, $ a_ (n1) $ знаходяться на побічної (другорядної) діагоналі; їх називають побічними діагональними елементами. Наприклад, для матриці $ C \u003d \\ left (\\ begin (array) (cccc) 2 & -2 & 9 & 1 \\\\ 5 & 9 & 8 & 0 \\\\ 1 & 0 & 4 & -7 \\\\ -4 & -9 & 5 & 6 \\ end (array) \\ right) $ маємо:

Елементи $ c_ (11) \u003d 2 $, $ c_ (22) \u003d 9 $, $ c_ (33) \u003d 4 $, $ c_ (44) \u003d 6 $ є головними діагональними елементами; елементи $ c_ (14) \u003d 1 $, $ c_ (23) \u003d 8 $, $ c_ (32) \u003d 0 $, $ c_ (41) \u003d - 4 $ - побічні діагональні елементи.
Сума головних діагональних елементів називається слідом матриці і позначається $ \\ Tr A $ (або $ \\ Sp A $):
$$ \\ Tr A \u003d a_ (11) + a_ (22) + \\ ldots + a_ (nn) $$
Наприклад, для матриці $ C \u003d \\ left (\\ begin (array) (cccc) 2 & -2 & 9 & 1 \\\\ 5 & 9 & 8 & 0 \\\\ 1 & 0 & 4 & -7 \\\\ - 4 & -9 & 5 & 6 \\ end (array) \\ right) $ маємо:
$$ \\ Tr C \u003d 2 + 9 + 4 + 6 \u003d 21. $$
Поняття діагональних елементів використовується також і для неквадратних матриць. Наприклад, для матриці $ B \u003d \\ left (\\ begin (array) (ccccc) 2 & -2 & 9 & 1 & 7 \\\\ 5 & -9 & 8 & 0 & -6 \\\\ 1 & 0 & 4 & - 7 & -6 \\ end (array) \\ right) $ головними діагональними елементами будуть $ b_ (11) \u003d 2 $, $ b_ (22) \u003d - 9 $, $ b_ (33) \u003d 4 $.
Види матриць в залежності від значень їх елементів.
Якщо всі елементи матриці $ A_ (m \\ times n) $ дорівнюють нулю, то така матриця називається нульовий і позначається зазвичай літерою $ O $. Наприклад, $ \\ left (\\ begin (array) (cc) 0 & 0 \\\\ 0 & 0 \\\\ 0 & 0 \\ end (array) \\ right) $, $ \\ left (\\ begin (array) (ccc) 0 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \\ end (array) \\ right) $ - нульові матриці.
Розглянемо деяку ненульову рядок матриці $ A $, тобто такий рядок, в якій є хоч один елемент, відмінний від нуля. провідним елементом ненульовий рядки назвемо її перший (рахуючи зліва направо) ненульовий елемент. Для прикладу розглянемо таку матрицю:
$$ W \u003d \\ left (\\ begin (array) (cccc) 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 12 \\\\ 0 & -9 & 5 & 9 \\ end (array) \\ right) $ $
У другому рядку провідним буде четвертий елемент, тобто $ W_ (24) \u003d 12 $, а в третьому рядку провідним буде другий елемент, тобто $ W_ (32) \u003d - 9 $.
Матриця $ A_ (m \\ times n) \u003d \\ left (a_ (ij) \\ right) $ називається ступінчастою, Якщо вона задовольняє двом умовам:
- Нульові рядки, якщо вони є, розташовані нижче всіх ненульових рядків.
- Номери провідних елементів ненульових рядків утворюють строго зростаючу послідовність, тобто якщо $ a_ (1k_1) $, $ a_ (2k_2) $, ..., $ a_ (rk_r) $ - провідні елементи ненульових рядків матриці $ A $, то $ k_1 \\ lt (k_2) \\ lt \\ ldots \\ lt ( k_r) $.
Приклади східчастих матриць:
$$ \\ left (\\ begin (array) (cccccc) 0 & 0 & 2 & 0 & -4 & 1 \\\\ 0 & 0 & 0 & 0 & -9 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\ end (array) \\ right); \\; \\ Left (\\ begin (array) (cccc) 5 & -2 & 2 & -8 \\\\ 0 & 4 & 0 & 0 \\\\ 0 & 0 & 0 & -10 \\ end (array) \\ right). $$
Для порівняння: матриця $ Q \u003d \\ left (\\ begin (array) (ccccc) 2 & -2 & 0 & 1 & 9 \\\\ 0 & 0 & 0 & 7 & 9 \\\\ 0 & -5 & 0 & 10 & 6 \\ end (array) \\ right) $ не є ступінчастою, так як порушено другу умову в визначенні ступінчастою матриці. Провідні елементи в другій і третій рядках $ q_ (24) \u003d 7 $ і $ q_ (32) \u003d 10 $ мають номера $ k_2 \u003d 4 $ і $ k_3 \u003d 2 $. Для ступінчастою матриці повинна бути виконана умова $ k_2 \\ lt (k_3) $, яке в даному випадку порушено. Зазначу, що якщо поміняти місцями другу і третю рядки, то отримаємо ступінчасту матрицю: $ \\ left (\\ begin (array) (ccccc) 2 & -2 & 0 & 1 & 9 \\\\ 0 & -5 & 0 & 10 & 6 \\\\ 0 & 0 & 0 & 7 & 9 \\ end (array) \\ right) $.
Ступінчасту матрицю називають трапецієподібної або трапецеидальной, Якщо для провідних елементів $ a_ (1k_1) $, $ a_ (2k_2) $, ..., $ a_ (rk_r) $ виконані умови $ k_1 \u003d 1 $, $ k_2 \u003d 2 $, ..., $ k_r \u003d r $, тобто провідними є діагональні елементи. У загальному вигляді трапецієвидну матрицю можна записати так:
$$ A_ (m \\ times (n)) \u003d \\ left (\\ begin (array) (cccccc) a_ (11) & a_ (12) & \\ ldots & a_ (1r) & \\ ldots & a_ (1n) \\\\ a_ (rr) & \\ ldots & a_ (rn) \\\\ 0 & 0 & \\ ldots & 0 & \\ ldots & 0 \\\\ \\ ldots & \\ ldots & \\ ldots & \\ ldots & \\ ldots & \\ ldots \\\\ 0 & 0 & \\ ldots & 0 & \\ ldots & 0 \\ end (array) \\ right) $$
Приклади трапецієподібних матриць:
$$ \\ left (\\ begin (array) (cccccc) 4 & 0 & 2 & 0 & -4 & 1 \\\\ 0 & -2 & 0 & 0 & -9 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 & 0 & 0 \\ end (array) \\ right); \\; \\ Left (\\ begin (array) (cccc) 5 & -2 & 2 & -8 \\\\ 0 & 4 & 0 & 0 \\\\ 0 & 0 & -3 & -10 \\ end (array) \\ right). $$
Дамо ще кілька визначень для квадратних матриць. Якщо всі елементи квадратної матриці, Розташовані під головною діагоналлю, дорівнюють нулю, то таку матрицю називають верхньої трикутною матрицею. Наприклад, $ \\ left (\\ begin (array) (cccc) 2 & -2 & 9 & 1 \\\\ 0 & 9 & 8 & 0 \\\\ 0 & 0 & 4 & -7 \\\\ 0 & 0 & 0 & 6 \\ end (array) \\ right) $ - верхня трикутна матриця. Зауважте, що у визначенні верхньої трикутної матриці нічого не сказано про значення елементів, розташованих над головною діагоналлю або на головній діагоналі. Вони можуть бути нульовими чи ні, - це несуттєво. Наприклад, $ \\ left (\\ begin (array) (ccc) 0 & 0 & 9 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \\ end (array) \\ right) $ - теж верхня трикутна матриця.
Якщо всі елементи квадратної матриці, розташовані над головною діагоналлю, дорівнюють нулю, то таку матрицю називають нижньої трикутної матрицею. Наприклад, $ \\ left (\\ begin (array) (cccc) 3 & 0 & 0 & 0 \\\\ -5 & 1 & 0 & 0 \\\\ 8 & 2 & 1 & 0 \\\\ 5 & 4 & 0 & 6 \\ Зауважте, що у визначенні нижньої трикутної матриці нічого не сказано про значення елементів, розташованих під або на головній діагоналі. Вони можуть бути нульовими чи ні, - це неважливо. Наприклад, $ \\ left (\\ begin (array) (ccc) -5 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 9 \\ end (array) \\ right) $ і $ \\ left (\\ begin (array) (ccc) 0 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \\ end (array) \\ right) $ - теж нижні трикутні матриці.
Квадратна матриця називається діагональної, Якщо всі елементи цієї матриці, що не лежать на головній діагоналі, дорівнюють нулю. Приклад: $ \\ left (\\ begin (array) (cccc) 3 & 0 & 0 & 0 \\\\ 0 & -2 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 6 \\ Елементи на головній діагоналі можуть бути будь-якими (рівними нулю чи ні), - це несуттєво.
Діагональна матриця називається одиничної, Якщо всі елементи цієї матриці, розташовані на головній діагоналі, дорівнюють 1. Наприклад, $ \\ left (\\ begin (array) (cccc) 1 & 0 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\ end (array) \\ right) $ - одинична матриця четвертого порядку; $ \\ Left (\\ begin (array) (cc) 1 & 0 \\\\ 0 & 1 \\ end (array) \\ right) $ - одинична матриця другого порядку.
У липні 2020 року NASA запускає експедицію на Марс. Космічний апарат доставить на Марс електронний носій з іменами всіх зареєстрованих учасників експедиції.
Реєстрація учасників відкрита. Отримайте свій квиток на Марс за цим посиланням.
Якщо цей пост вирішив вашу проблему або просто сподобався вам, поділіться посиланням на нього зі своїми друзями в соціальних мережах.
Один з цих варіантів коду потрібно скопіювати і вставити в код вашої веб-станиці, бажано між тегами
і або ж відразу після тега . За першим варіантом MathJax подгружается швидше і менше гальмує сторінку. Зате другий варіант автоматично відстежує і підвантажує свіжі версії MathJax. Якщо вставити перший код, то його потрібно буде періодично оновлювати. Якщо вставити другий код, то сторінки будуть завантажуватися повільніше, зате вам не потрібно буде постійно стежити за оновленнями MathJax.Підключити MathJax найпростіше в Blogger або WordPress: в панелі управління сайтом додайте віджет, призначений для вставки стороннього коду JavaScript, скопіюйте в нього перший або другий варіант коду завантаження, представленого вище, і розмістіть віджет ближче до початку шаблону (до речі, це зовсім не обов'язково , оскільки скрипт MathJax завантажується асинхронно). От і все. Тепер вивчіть синтаксис розмітки MathML, LaTeX і ASCIIMathML, і ви готові вставляти математичні формули на веб-сторінки свого сайту.
Черговий напередодні Нового Року ... морозна погода і сніжинки на віконному склі ... Все це спонукало мене знову написати про ... фракталах, і про те, що знає про це Вольфрам Альфа. З цього приводу є цікава стаття, в якій є приклади двовимірних фрактальних структур. Тут же ми розглянемо більш складні приклади тривимірних фракталів.
Фрактал можна наочно уявити (описати), як геометричну фігуру або тіло (маючи на увазі, що і те і інше є безліч, в даному випадку, безліч точок), деталі якої мають таку ж форму, як і сама вихідна фігура. Тобто, це самоподібна структура, розглядаючи деталі якої при збільшенні, ми будемо бачити ту ж саму форму, що й без збільшення. Тоді як у випадку звичайної геометричної фігури (НЕ фрактала), при збільшенні ми побачимо деталі, які мають більш просту форму, Ніж сама вихідна фігура. Наприклад, при досить великому збільшенні частина еліпса виглядає, як відрізок прямої. З фракталами такого не відбувається: при будь-якому їх збільшенні ми знову побачимо ту ж саму складну форму, яка з кожним збільшенням буде повторюватися знову і знову.
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки про фрактали, в своїй статті Фрактали і мистецтво в ім'я науки написав: "Фрактали - це геометричні форми, які в рівній мірі складні в своїх деталях, як і в своїй загальній формі. Тобто, якщо частина фрактала буде збільшена до розміру цілого, вона буде виглядати, як ціле, або в точності, або, можливо, з невеликою деформацією ".
Щоб привести матрицю до ступінчастого вигляду (рис. 1.4), потрібно виконати наступні дії.
1. У першому стовпці вибрати елемент, відмінний від нуля ( провідний елемент ). Рядок з провідним елементом ( провідна рядок ), Якщо вона не перша, переставити на місце першого рядка (перетворення I типу). Якщо в першому стовпці немає ведучого (всі елементи дорівнюють нулю), то виключаємо цей стовпець, і продовжуємо пошук провідного елементу в решти матриці. Перетворення закінчуються, якщо виключені всі стовпці або в частині матриці всі елементи нульові.
2. Розділити всі елементи провідного рядка на провідний елемент (перетворення II типу). Якщо провідна рядок остання, то на цьому перетворення слід закінчити.
3. До кожної рядку, розташованої нижче провідною, додати провідний рядок, помножену відповідно на таке число, щоб елементи, які стоять під провідним виявилися рівними нулю (перетворення III типу).
4. Виключивши з розгляду рядок і стовпець, на перетині яких стоїть провідний елемент, перейти до пункту 1, в якому всі описані дії застосовуються до решти матриці.
Теорема про розклад візначніка по елементів рядка.
Теорема про розкладання визначника за елементами рядка або стовпця дозволяє звести обчислення визначника - го порядку () до обчислення визначників порядку .
Якщо визначник має рівні нулю елементи, то зручніше за все розкладати визначник за елементами тієї рядки або стовпці, який містить найбільшу кількість нулів.
Використовуючи властивості визначників, можна перетворити визначник - го порядку так, щоб всі елементи деякого рядка або стовпця, крім одного, стали рівними нулю. Таким чином, обчислення визначника - го порядку, якщо він відмінний від нуля, зведеться до обчислення одного визначника - го порядку.
Завдання 3.1.обчислити визначник
Рішення.Додавши до другої рядку першу, до третьої - першу, помножену на 2, до четвертої - першу, помножену на -5, отримаємо
Розкладаючи визначник за елементами першого стовпчика, маємо
![]() .
.
В отриманому визначнику 3-го порядку звернемо в нуль всі елементи першого стовпчика, крім першого. Для цього до другої рядку додамо першу, помножену на (-1), до третьої, помноженої на 5, додамо першу, помножену на 8. Так як множили третій рядок на 5, то (для того, щоб визначник не змінився) помножимо його на . маємо
Отриманий визначник розкладемо за елементами першого стовпця:
Теорема Лапласа (1). Теорема про чужі ДОПОВНЕННЯ (2)
1) Определітельравенсуммепроізведеній елементів якого-небудь рядка на іхалгебраіческіедополненія.
2) Суммапроізведенійелементовкакой-якого рядка визначника на алгебраїчні доповнення відповідних елементів іншого його рядки дорівнює нулю (теорема про примноження на чужі алгебраїчні доповнення).
Будь-яка точка на площині при вибраній системі координат задається парою (α, β) своїх координат; числа α і β можна розуміти також як координати радіуса-вектора з кінцем в цій точці. Аналогічно, в просторі трійка (α, β, γ) визначає точку або вектор з координатами α, β, γ. Саме на цьому грунтується добре відома читачеві геометрична інтерпретація систем лінійних рівнянь з двома або трьома невідомими. Так, в разі системи двох лінійних рівнянь з двома невідомими
а 1 х + b 1 у \u003d с 1,
а 2 х + b 2 у \u003d з 2
кожне з рівнянь тлумачиться як пряма на площині (див. рис. 26), а рішення (α, β) - як точка перетину цих прямих або як вектор з координатами аїр (рисунок відповідає випадку, коли система має єдине рішення).
 Мал. 26
Мал. 26
Аналогічно можна вчинити з системою лінійних рівнянь з трьома невідомими, інтерпретуючи кожне рівняння як рівняння площини в просторі.
В математиці і різних її додатках (зокрема, в теорії кодування) доводиться мати справу з системами лінійних рівнянь, що містять більше трьох невідомих. Системою лінійних рівнянь з n невідомими x 1, х 2, ..., х n називається сукупність рівнянь виду
а 11 х 1 + а 12 х 2 + ... + а 1n х n \u003d b 1,
а 21 х 1 + а 22 х 2 + ... + а 2n х n \u003d b 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
а m1 х 1 + а m2 х 2 + ... + а mn х n \u003d b m,
де a ij і b i - довільні дійсні числа. Число рівнянь в системі може бути будь-яким і ніяк не пов'язане з числом невідомих. Коефіцієнти при невідомих а ij мають подвійну нумерацію: перший індекс i вказує номер рівняння, другий індекс j - номер невідомого, при якому варто даний коефіцієнт. Будь-яке рішення системи розуміється як набір (дійсних) значень невідомих (α 1, α 2, ..., α n), що звертають кожне рівняння в правильну рівність.
Хоча безпосереднє геометричне тлумачення системи (1) при n\u003e 3 вже неможливо, однак цілком можливо і в багатьох відносинах зручно поширити на випадок довільного n геометричний мову простору двох або трьох вимірів. Цій меті і служать подальші визначення.
Всякий упорядкований набір з n дійсних чисел (α 1, α 2, ..., α n) називається n-мірним арифметичним вектором, а самі числа α 1, α 2, ..., α n - координатами цього вектора.
Для позначення векторів використовується, як правило, жирний шрифт і для вектора а з координатами α 1, α 2, ..., α n зберігається звичайна форма запису:
а \u003d (α 1, α 2, ..., α n).
За аналогією зі звичайною площиною безліч всіх n-мірних векторів, що задовольняють лінійним рівнянням з n невідомими, називають гиперплоскостью в n-вимірному просторі. При такому визначенні безліч всіх рішень системи (1) є не що інше, як перетин кількох гіперплоскостей.
Додавання і множення n-мірних векторів визначаються за тими ж правилами, що і для звичайних векторів. А саме, якщо
а \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Два n-мірних вектора, то їх сумою називається вектор
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
Твором вектора а на число λ називається вектор
λа \u003d (λα 1, λα 2, ..., λα n). (4)
Безліч всіх n-мірних арифметичних векторів з операціями додавання векторів і множення вектора на число називається арифметичним n-мірним векторних простором L n.
Використовуючи введені операції, можна розглядати довільні лінійні комбінації декількох векторів, т. Е. Вирази виду
λ 1 a 1 + λ 2 a 2 + ... + λ k a k,
де λ i - дійсні числа. Наприклад, лінійна комбінація векторів (2) з коефіцієнтами λ і μ - це вектор
λа + μb \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
У тривимірному просторі векторів особливу роль відіграє трійка векторів i, j, k (координатні орти), за якими розкладається будь-який вектор а:
a \u003d xi + yj + zk,
де х, у, z - дійсні числа (координати вектора а).
В n-вимірному випадку таку ж роль відіграє наступна система векторів:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Всякий вектор а є, очевидно, лінійна комбінація векторів е 1, e 2, ..., e n:
а \u003d а 1 е 1 + а 2 е 2 + ... + а n е n, (6)
причому коефіцієнти α 1, α 2, ..., α n збігаються з координатами вектора а.
Позначаючи через 0 вектор, всі координати якого дорівнюють нулю (коротко, нульовий вектор), введемо наступну важливу визначення:
Система векторів а 1, а 2, ..., а k називається лінійно залежною, якщо існує рівна нульового вектору лінійна комбінація
λ 1 a 1 + λ 2 a 2 + ... + λ k a k \u003d 0,
в якій хоча б один з коефіцієнтів h 1, λ 2, ..., λ k різниться від нуля. В іншому випадку система називається лінійно незалежною.
Так, вектори
а 1 \u003d (1, 0, 1, 1), а 2 \u003d (1, 2, 1, 1), а 3 \u003d (2, 2, 2, 2)
лінійно залежні, оскільки
a 1 + a 2 - а 3 \u003d 0.
Лінійна залежність, як видно з визначення, рівносильна (при k ≥ 2) того, що хоча б один з векторів системи є лінійною комбінацією інших.
Якщо система складається з двох векторів a 1, а 2, то лінійна залежність системи означає, що один з векторів пропорційний іншому, скажімо, а 1 \u003d λа 2; в тривимірному випадку це рівносильно коллинеарности векторів а 1 і а 2. Точно так же лінійна залежність системи I з трьох векторів в звичайному просторі означає компланарність цих векторів. Поняття лінійної залежності є, таким чином, природним узагальненням понять коллинеарности і компланарності.
Неважко переконатися, що вектори е 1, е 2, ..., е n з системи (5) лінійно незалежні. Отже, в n-вимірному просторі існують системи з n лінійно незалежних векторів. Можна показати, що будь-яка система з більшого числа векторів лінійно залежна.
Будь-яка система a 1, а 2, ..., а n з n лінійно незалежних векторів n-мірного простору L n називається його базисом.
Будь-вектор а простору L n розкладається, і до того ж єдиним чином, по векторах довільного базису a 1, а 2, ..., а n:
а \u003d λ 1 a 1 + λ 2 a 2 + ... + λ n a n.
Цей факт легко встановлюється на підставі визначення базису.
Продовжуючи аналогію з тривимірним простором, можна і в n-вимірному випадку визначити скалярний твір а · b векторів, вважаючи
a · b \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
При такому визначенні зберігаються всі основні властивості скалярного твори тривимірних векторів. Вектори а і b називаються ортогональними, якщо їх скалярний добуток дорівнює нулю:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
В теорії лінійних кодів використовується ще одне важливе поняття - поняття підпростору. Підмножина V простору L n називається подпространством цього простору, якщо
1) для будь-яких векторів а, b, що належать V, їх сума а + b також належить V;
2) для будь-якого вектора а, що належить V, і для будь-якого дійсного числа λ вектор λа також належить V.
Наприклад, безліч всіх лінійних комбінацій векторів e 1, е 2 з системи (5) буде подпространством простору L n.
У лінійної алгебрі доводиться, що у всякому підпросторі V існує така лінійно незалежна система векторів a 1, a 2, ..., a k, що всякий вектор а підпростору є лінійною комбінацією цих векторів:
a \u003d λ 1 a 1 + λ 2 a 2 + ... + λ k a k.
Зазначена система векторів називається базисом підпростору V.
З визначення простору і підпростори безпосередньо випливає, що простір L n є комутативна група щодо операції додавання векторів, а будь-яке його підпростір V є підгрупою цієї групи. У цьому сенсі можна, наприклад, розглядати суміжні класи простору L n по подпространству V.
На закінчення підкреслимо, що якщо в теорії n-мірного арифметичного простору замість дійсних чисел (т. Е. Елементів поля дійсних чисел) розглядати елементи довільного поля F, то все визначення і факти, наведені вище, зберегли б силу.
В теорії кодування важливу роль відіграє випадок, коли поле F поле відрахувань Z p, яке, як ми знаємо, звичайно. В цьому випадку відповідне n-мірний простір також звичайно і містить, як неважко бачити, р n елементів.
Поняття простору, як і поняття групи і кільця, допускає також і аксіоматичне визначення. За подробицями ми відсилаємо живильник до будь-якого курсу лінійної алгебри.
Лінійна комбінація. Лінійно залежні та незалежні системи векторів.
інейная комбінація векторів
Лінійною комбінацією векторів ![]() називають вектор
називають вектор
де ![]() - коефіцієнти лінійної комбінації. якщо
- коефіцієнти лінійної комбінації. якщо ![]() комбінація називається тривіальною, якщо-нетривіальною.
комбінація називається тривіальною, якщо-нетривіальною.
Лінійна залежність і незалежність векторів
система ![]() лінійно завісімачто
лінійно завісімачто 
система ![]() лінійно незалежна
лінійно незалежна 
Критерій лінійної залежності векторів
Для того щоб вектори ![]() (r\u003e 1) Були лінійно залежні, необхідно і достатньо, щоб хоча б один з цих векторів був лінійною комбінацією інших.
(r\u003e 1) Були лінійно залежні, необхідно і достатньо, щоб хоча б один з цих векторів був лінійною комбінацією інших.
Розмірність лінійного простору
лінійне простір Vназивається n-мірним (має розмірність n), Якщо в ньому:
1) існує nлінійно незалежних векторів;
2) будь-яка система n + 1векторів лінійно залежна.
позначення: n\u003d dim V;.
Система векторів називається лінійно залежною,якщо існує ненульовийнаборчіселтакіх, що лінійна комбінація
Система векторів називається лінійно незалежної,якщо з рівності нулю лінійної комбінації
слід рівність нулю всіхкоефіцієнтів
Питання про лінійну залежність векторів в загальному випадку зводиться до питання про існування ненульового рішення у однорідної системи лінійних рівнянь з коефіцієнтами, рівними відповідним координатам даних векторів.
Для того щоб добре засвоїти поняття «лінійна залежність», «лінійна незалежність» системи векторів, корисно вирішити завдання наступного типу:
Лінійна залежність.І і ІІ Критерії лінійної залежності.
система векторів лінійно залежна тоді і тільки тоді, коли один з векторів системи є лінійною комбінацією інших векторів цієї системи.
Доведення. Нехай система векторів лінійно залежна. Тоді існує такий набір коефіцієнтів ![]() , Що, причому хоча б один коефіцієнт відмінний від нуля. Припустимо, що . тоді
, Що, причому хоча б один коефіцієнт відмінний від нуля. Припустимо, що . тоді
тобто є лінійною комбінацією інших векторів системи.
Нехай один з векторів системи є лінійною комбінацією інших векторів. Припустимо, що це вектор, тобто ![]() . Очевидно, що . Отримали, що лінійна комбінація векторів системи дорівнює нулю, причому один з коефіцієнтів відмінний від нуля (дорівнює).
. Очевидно, що . Отримали, що лінійна комбінація векторів системи дорівнює нулю, причому один з коефіцієнтів відмінний від нуля (дорівнює).
Речення10 . 7 Якщо система векторів містить лінійно залежну підсистему, то вся система лінійно залежна.
Доведення.
Нехай в системі векторів підсистема ![]() ,, Є лінійно залежною, тобто, і хоча б один коефіцієнт відмінний від нуля. Тоді складемо лінійну комбінацію. Очевидно, що ця лінійна комбінація дорівнює нулю, і що серед коефіцієнтів є ненульовий.
,, Є лінійно залежною, тобто, і хоча б один коефіцієнт відмінний від нуля. Тоді складемо лінійну комбінацію. Очевидно, що ця лінійна комбінація дорівнює нулю, і що серед коефіцієнтів є ненульовий.
База системи векторів, ее Основна властівість.
Базою ненульовий системи векторів називається еквівалентна їй лінійно незалежна підсистема. Нульова система бази не має.
Властивість 1:База лінійної незалежної системи збігається з нею самою.
приклад: Система лінійно незалежних векторів оскільки жоден з векторів не може бути лінійно вирожен через інші.
Властивість 2: (Критерій Бази)Лінійно незалежна підсистема даної системи є її базою тоді і тільки тоді, коли вона максимально лінійно незалежна.
Доведення:дана система необхідність Нехай база. Тоді за визначенням і, якщо, де, система лінійно залежна, так як лінійно вирожается через, отже максимально лінійно незалежна. достатністьНехай максимально лінійно незалежна підсистема, тоді де. лінійно залежна лінійно вирожается через отже база системи.
Властивість 3: (Основна властивість бази)Кожен вектор системи вирожается через базу єдиним чином.
ДоведенняНехай вектор вирожается через базу двома способами, тоді:, тоді
Ранг системи векторів.
|
визначення:Рангом ненульовий системи векторів лінійного простору називається число векторів її бази. Ранг нульової системи за визначенням дорівнює нулю. Властивості рангу:1) Ранг лінійно незалежної системи збігається з числом її векторів. 2) Ранг лінійно залежною системи менше числа її векторів. 3) Ранги еквівалентних систем збігаються -rankrank. 4) Ранг під системи менше або дорівнює рангу системи. 5) Есліі rankrank, тогдаіімеют загальну базу. 6) Ранг системи не змінити, якщо в неї додати вектор, який є лінійною комбінацією інших векторів системи. 7) Ранг системи не змінити, якщо з неї видалити вектор, який є лінійною комбінацією інших векторів. |
Для знаходження рангу системи векторів, потрібно використовувати метод Гауссаі привести систему до трикутної або трапецієподібної формі.
Еквівалентні системи векторів.
приклад:
Перетворимо дані вектора в матрицю для знаходження бази. отримаємо: 
Тепер за допомогою методу Гаусса будемо преобразоивавать матрицю до трапецеидальному увазі:
1) У нашій основний матриці, будемо анулювати весь перший стовпець крім першого рядка від другої віднімаючи першу помножену на, від третьої віднімаючи першу помножену на, а від четвётой ми нічого не будемо віднімати так як перший елемент четвертої рядки, тобто перетин першого шпальти і четвертої рядки, дорівнює нулю. Отримаємо матрицю:  2) Тепер в матриці, поміняємо місцями рядки 2, 3 і 4 для простоти рішення, що б на місці елемента була одиниця. Четверту рядок поміняємо поставимо замість другої, другу замість третьої і третю на місце четвертої. Отримаємо матрицю:
2) Тепер в матриці, поміняємо місцями рядки 2, 3 і 4 для простоти рішення, що б на місці елемента була одиниця. Четверту рядок поміняємо поставимо замість другої, другу замість третьої і третю на місце четвертої. Отримаємо матрицю:  3) В матриці ануліруем всі елементи під елементом. Оскільки знову елемент нашої матреці дорівнює нулю, ми нічого не забираємо від четвертої рядки, а до третьої додамо другу помножену на. Отримаємо матрицю:
3) В матриці ануліруем всі елементи під елементом. Оскільки знову елемент нашої матреці дорівнює нулю, ми нічого не забираємо від четвертої рядки, а до третьої додамо другу помножену на. Отримаємо матрицю:  4) Знову поміняємо в матриці рядка 3 і 4 місцями. Отримаємо матрицю:
4) Знову поміняємо в матриці рядка 3 і 4 місцями. Отримаємо матрицю:  5) В матріцепрібавім до червётрой рядку третю, помножену на 5. Отримаємо матрицю, яка буде мати трикутний вигляд:
5) В матріцепрібавім до червётрой рядку третю, помножену на 5. Отримаємо матрицю, яка буде мати трикутний вигляд: 
Системи, їх ранги збігаються в силу властивостей рангу і їх ранг дорівнює rank rank
зауваження:1) На відміну від традиційного методу Гаусса, якщо в рядку матриці всі елементи діляться на певне число, ми не маємо право скорочувати її рядок в силу дії властивостей матриці. Якщо ми захочемо скоротити рядок на певне число, доведеться скорочувати всю матрицю на це число. 2) В разі, якщо ми отримаємо лінійно залежну рядок, ми можемо її прибрати з нашого матриці і замінити на нульову рядок. приклад:
 Відразу видно що другий рядок виражається через першу, якщо помножити першу на 2. В Тіаком випадку можемо замінити всю другий рядок на нульову. отримаємо:
Відразу видно що другий рядок виражається через першу, якщо помножити першу на 2. В Тіаком випадку можемо замінити всю другий рядок на нульову. отримаємо:  У підсумку, привівши матрицю, або до трикутного, або до трапецеидальному увазі, де у неї немає лінійно залежних векторів, все не нульові вектори матриці і будуть базою матриці, а їх кількість рангом.
У підсумку, привівши матрицю, або до трикутного, або до трапецеидальному увазі, де у неї немає лінійно залежних векторів, все не нульові вектори матриці і будуть базою матриці, а їх кількість рангом.
Ось так само приклад системи векторів у вигляді графіка: Дана система де,, і. Базою даної системи очевидно буду вектора і, оскільки через них виражаються вектори. Дана система в графічному вигляді буде мати вигляд:
Елементарні превращение. Системи ступінчатого виду.
Елементарні перетворення матриці - це такі перетворення матриці, в результаті яких зберігається еквівалентність матриць. Таким чином, елементарні перетворення не змінюють безліч рішень системи лінійних алгебраїчних рівнянь, яку представляє ця матриця.
Елементарні перетворення використовуються в методі Гаусса для приведення матриці до трикутного або ступенчатому увазі.
Елементарними перетвореннями рядків називають:
У деяких курсах лінійної алгебри перестановка рядків матриці не виділяється в окреме елементарне перетворення в силу того, що перестановку місцями будь-яких двох рядків матриці можна отримати, використовуючи множення будь-якого рядка матриці на константу, і додаток до будь-якому рядку матриці іншого рядка, помноженої на константу,.
аналогічно визначаються елементарні перетворення стовпців.
елементарні перетворення оборотні.
Позначення вказує на те, що матриця може бути отримана з шляхом елементарних перетворень (або навпаки).
визначення
Квадратна матриця називається діагональної, Якщо всі її елементи, що стоять поза головною діагоналі, дорівнюють нулю.
Зауваження. Діагональні елементи матриці (тобто елементи, які стоять на головній діагоналі) можуть також дорівнювати нулю.
приклад

визначення
скалярною називається діагональна матриця, у якої все діагональні елементи рівні між собою.
Зауваження. Якщо нульова матриця є квадратної, то вона також є і скалярною.
приклад
![]()
визначення
одиничною матрицею називається скалярна матриця порядку, діагональні елементи якої рівні 1.
Зауваження. Для скорочення запису порядок одиничної матриці можна не писати, тоді одинична матриця позначається просто.
приклад
![]() - одинична матриця другого порядку.
- одинична матриця другого порядку.
2.10. Приведення матриці до діагонального вигляду
Нормальну (зокрема симетричну) матрицю A можна привести до діагонального вигляду перетворенням подібності -
A = TΛT −1
тут Λ \u003d Diag (λ 1, ..., λ N) - це діагональна матриця, елементами якої є власні значення матриці A, а T - це матриця, складена з відповідних власних векторів матриці A, Тобто T = (v 1 ,...,v N).
наприклад,

Мал. 23 Приведення до діагонального вигляду
ступінчаста матриця
визначення
ступінчастою називається матриця, яка задовольняє таким умовам:
визначення
ступінчастою називається матриця, яка містить рядків і у якій перші діагональних елементів ненульові, а елементи, що лежать нижче головної діагоналі і елементи останніх рядків дорівнюють нулю, тобто це матриця виду:

визначення
головним елементом деякою рядки матриці називається її перший ненульовий елемент.
приклад
Завдання. Визначити основні елементи кожного рядка матриці ![]()
Рішення. Головний елемент першого рядка - це перший ненульовий елемент цього рядка, а тому - головний елемент рядка під номером 1; аналогічно - головний елемент другого рядка.
Інше визначення ступінчастою матриці.
визначення
матриця називається ступінчастою, Якщо:
всі її нульові рядки стоять після ненульових;
в кожній ненульовий рядку, починаючи з другого, її головний елемент варто правіше (в стовпці з великим номером) головного елемента попереднього рядка.
За визначенням до ступінчастим матрицями будемо відносити нульову матрицю, а також матрицю, яка містить один рядок.
приклад
Приклади східчастих матриць:
![]() , ,
, ,  ,
,  ,
,
Приклади матриць, які не є ступінчастими:
![]() ,
,  ,
, 
приклад
Завдання. З'ясувати, чи є матриця  ступінчастою.
ступінчастою.
Рішення. Перевіряємо виконання умов з визначення:
Отже, задана матриця є ступінчастою.
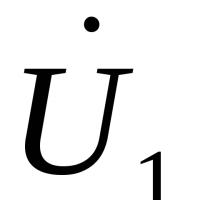 Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок
Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок Ефективний пошук роботи Курс з пошуку роботи
Ефективний пошук роботи Курс з пошуку роботи Основні характеристики і параметри фотодіода
Основні характеристики і параметри фотодіода Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF
Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF Чому згорнуте вікно програми довго розгортається?
Чому згорнуте вікно програми довго розгортається? DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt
DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt Що робити якщо пропав курсор миші
Що робити якщо пропав курсор миші