Pe Internet, inclusiv pe Habré, puteți găsi o mulțime de informații despre filtrul Kalman. Dar este greu de găsit o derivație ușor digerabilă a formulelor în sine. Fără o concluzie, toată această știință este percepută ca un fel de șamanism, formulele arată ca un set fără chip de simboluri și, cel mai important, multe afirmații simple care se află la suprafața unei teorii sunt dincolo de înțelegere. Scopul acestui articol va fi acela de a vorbi despre acest filtru într-un limbaj cât mai accesibil.
Filtrul Kalman este un instrument puternic de filtrare a datelor. Principiul său principal este că la filtrare se utilizează informații despre fizica fenomenului în sine. De exemplu, dacă filtrați datele din vitezometrul unei mașini, atunci inerția mașinii vă oferă dreptul de a percepe salturi prea rapide de viteză ca o eroare de măsurare. Filtrul Kalman este interesant pentru că, într-un fel, este cel mai bun filtru. Vom discuta mai detaliat mai jos ce înseamnă exact cuvintele „cel mai bun”. La finalul articolului voi arăta că în multe cazuri formulele pot fi simplificate în așa măsură încât aproape nimic nu va rămâne din ele.

Program educațional

Înainte de a face cunoștință cu filtrul Kalman, îmi propun să reamintesc câteva definiții și fapte simple din teoria probabilității.

Valoare aleatoare

Când spun că este dată o variabilă aleatoare, înseamnă că această cantitate poate lua valori aleatoare. Ia valori diferite cu probabilități diferite. Când aruncați, să zicem, un zar, un set discret de valori va renunța:. Când vine vorba, de exemplu, de viteza unei particule rătăcitoare, atunci, evident, trebuie să se ocupe de un set continuu de valori. Vom nota valorile „eliminate” ale unei variabile aleatoare cu, dar uneori, vom folosi aceeași literă, pe care o folosim pentru a desemna o variabilă aleatoare:.
În cazul unui set continuu de valori, variabila aleatoare se caracterizează prin densitatea de probabilitate, care ne dictează că probabilitatea ca variabila aleatoare să „cădă” într-o mică vecinătate a unui punct cu lungime este egală cu. După cum putem vedea din imagine, această probabilitate este egală cu aria dreptunghiului umbrit de sub grafic:

Destul de des în viață, variabilele aleatoare sunt gaussiene când densitatea de probabilitate este egală.

Vedem ca functia are forma unui clopot centrat intr-un punct si cu o latime caracteristica ordinului.
Întrucât vorbim despre distribuția Gauss, ar fi un păcat să nu mai vorbim de unde a venit. Așa cum numerele sunt bine stabilite în matematică și apar în locurile cele mai neașteptate, tot așa și distribuția gaussiană și-a luat rădăcini adânci în teoria probabilității. O afirmație remarcabilă care explică parțial omniprezența gaussiană este următoarea:
Să existe o variabilă aleatoare cu o distribuție arbitrară (de fapt, există unele restricții asupra acestui arbitrar, dar nu sunt deloc stricte). Să efectuăm experimente și să calculăm suma valorilor „abandonate” ale variabilei aleatoare. Să facem multe dintre aceste experimente. Este clar că de fiecare dată vom primi o valoare diferită a sumei. Cu alte cuvinte, această sumă este ea însăși o variabilă aleatoare cu propria sa lege de distribuție. Se dovedește că pentru suficient de mare legea distribuției acestei sume tinde către distribuția gaussiană (apropo, lățimea caracteristică a „clopotului” crește ca). Citiți mai multe în Wikipedia: Teorema limitei centrale. În viață, de foarte multe ori există cantități care sunt alcătuite dintr-un număr mare de variabile aleatoare independente distribuite egal și, prin urmare, sunt distribuite conform gaussianului.

Rău

Valoarea medie a unei variabile aleatoare este ceea ce obținem în limită dacă efectuăm o mulțime de experimente și calculăm media aritmetică a valorilor scăzute. Media este desemnată în moduri diferite: matematicienilor le place să desemneze prin (așteptare), iar matematicienilor străini prin (așteptare). Fizicienii sunt prin sau. Vom desemna în mod străin:.
De exemplu, pentru o distribuție Gaussiană, media este.

Dispersia

În cazul distribuției gaussiene, vedem clar că variabila aleatoare preferă să cadă în apropierea valorii sale medii. După cum se poate observa din grafic, împrăștierea caracteristică a valorilor de ordine. Cum putem estima această răspândire a valorilor pentru o variabilă aleatoare arbitrară, dacă îi cunoaștem distribuția. Puteți desena un grafic al densității sale de probabilitate și puteți estima lățimea caracteristică cu ochiul. Dar preferăm să mergem pe calea algebrică. Puteți găsi lungimea medie a abaterii (modulului) de la medie:. Această valoare va fi o bună estimare a împrăștierii caracteristice a valorilor. Dar tu și cu mine știm foarte bine că folosirea modulelor în formule este o durere de cap, așa că această formulă este rar folosită pentru a estima răspândirea caracteristică.
O modalitate mai ușoară (simple din punct de vedere al calculelor) este să găsești. Această valoare se numește varianță și este adesea menționată ca. Rădăcina varianței se numește abatere standard. Abaterea standard este o estimare bună a răspândirii unei variabile aleatorii.
De exemplu, pentru o distribuție Gaussiană, putem calcula că varianța definită mai sus este exact egală, ceea ce înseamnă că abaterea standard este egală, ceea ce este de acord foarte bine cu intuiția noastră geometrică.
De fapt, există o mică fraudă ascunsă aici. Cert este că în definiția distribuției gaussiene, sub exponent se află expresia. Aceste două din numitor sunt tocmai astfel încât abaterea standard să fie egală cu coeficientul. Adică formula de distribuție gaussiană în sine este scrisă într-o formă special ascuțită, astfel încât să luăm în considerare abaterea ei standard.

Variabile aleatoare independente

Variabilele aleatoare sunt dependente și nu. Imaginați-vă că aruncați un ac pe un avion și notați coordonatele ambelor capete. Aceste două coordonate sunt dependente, sunt legate de condiția ca distanța dintre ele să fie întotdeauna egală cu lungimea acului, deși sunt valori aleatorii.
Variabilele aleatoare sunt independente dacă rezultatul primei dintre ele este complet independent de rezultatul celei de-a doua dintre ele. Dacă variabilele aleatoare sunt independente, atunci valoarea medie a produsului lor este egală cu produsul valorilor lor medii:

Dovada

De exemplu, a avea ochi albaștri și a absolvi liceul cu o medalie de aur sunt variabile aleatoare independente. Dacă medaliați cu ochi albaștri, să zicem, medaliați cu aur, atunci medaliați cu ochi albaștri. Acest exemplu ne spune că, dacă variabilele aleatoare sunt date de densitățile lor de probabilitate, atunci independența acestor valori este exprimată prin faptul că densitatea probabilității ( prima valoare a renunțat, iar a doua) se găsește prin formula:

Din aceasta rezultă imediat că:

După cum puteți vedea, demonstrația este efectuată pentru variabile aleatoare care au un spectru continuu de valori și sunt date de densitatea lor de probabilitate. În alte cazuri, ideea de dovadă este similară.

filtru Kalman

Formularea problemei

Să notăm după valoarea pe care o vom măsura și apoi să filtram. Acestea pot fi coordonate, viteză, accelerație, umiditate, miros, temperatură, presiune etc.
Să începem cu un exemplu simplu care ne va conduce la formularea unei probleme generale. Imaginați-vă că avem o mașină controlată prin radio care poate merge doar înainte și înapoi. Cunoscând greutatea mașinii, forma, suprafața drumului etc., am calculat modul în care joystick-ul de control afectează viteza de mișcare.

Apoi coordonatele mașinii se vor schimba conform legii:

În viața reală, nu putem ține cont în calculele noastre de micile perturbații care acționează asupra mașinii (vânt, denivelări, pietricele de pe drum), astfel încât viteza reală a mașinii va diferi de cea calculată. O variabilă aleatorie este adăugată în partea dreaptă a ecuației scrise:

Avem instalat pe o mașină de scris un senzor GPS, care încearcă să măsoare adevărata coordonată a mașinii și, desigur, nu o poate măsura exact, ci o măsoară cu o eroare, care este și o variabilă aleatorie. Ca urmare, primim date eronate de la senzor:

Sarcina este ca, cunoscând citirile greșite ale senzorului, să găsească o bună aproximare pentru coordonatele adevărate a mașinii.
În formularea sarcinii generale, orice poate fi responsabil pentru coordonată (temperatură, umiditate ...), iar termenul responsabil pentru controlul sistemului din exterior va fi notat cu (în exemplul cu o mașină). Ecuațiile pentru citirile de coordonate și senzori vor arăta astfel:

Să discutăm în detaliu ce știm:

Este de remarcat faptul că sarcina de filtrare nu este o sarcină anti-aliasing. Nu încercăm să netezim datele de la senzor, încercăm să obținem cea mai apropiată valoare de coordonata reală.

algoritmul lui Kalman

Vom argumenta prin inducție. Imaginați-vă că la pasul al treilea am găsit deja valoarea filtrată de la senzor, care aproximează bine coordonatele adevărate a sistemului. Nu uitați că cunoaștem ecuația care controlează modificarea coordonatei necunoscute:

prin urmare, neprimind inca valoarea de la senzor, putem presupune ca la un pas sistemul evolueaza conform acestei legi si senzorul va arata ceva apropiat. Din păcate, nu putem spune nimic mai precis până acum. Pe de altă parte, la un pas, vom avea o citire inexactă a senzorului pe mâini.
Ideea lui Kalman este următoarea. Pentru a obține cea mai bună aproximare a coordonatei adevărate, trebuie să alegem calea de mijloc între citirea unui senzor inexact și predicția noastră despre ceea ce ne așteptam de la acesta. Vom acorda greutate citirii senzorului și greutatea va rămâne pe valoarea prezisă:

Coeficientul se numește coeficient Kalman. Depinde de pasul de iterație, așa că mai corect ar fi să-l scriem, dar deocamdată, pentru a nu aglomera formulele de calcul, vom omite indicele lui.
Trebuie să alegem coeficientul Kalman astfel încât valoarea coordonatei optime rezultată să fie cea mai apropiată de cea adevărată. De exemplu, dacă știm că senzorul nostru este foarte precis, atunci vom avea mai multă încredere în citirea lui și vom acorda mai multă greutate valorii (aproape de una). Dacă senzorul, dimpotrivă, este complet inexact, atunci ne vom concentra mai mult pe valoarea prezisă teoretic.
În general, pentru a găsi valoarea exactă a coeficientului Kalman, trebuie doar să minimizați eroarea:

Folosim ecuațiile (1) (cele din caseta cu fundal albastru) pentru a rescrie expresia erorii:

Dovada

Acum este momentul să discutăm ce înseamnă expresia minimizați eroarea? La urma urmei, eroarea, după cum putem vedea, este ea însăși o variabilă aleatorie și de fiecare dată ia valori diferite. De fapt, nu există o abordare unică pentru a defini ceea ce înseamnă că eroarea este minimă. La fel ca și în cazul varianței unei variabile aleatoare, când am încercat să estimăm lățimea caracteristică a răspândirii acesteia, așa că aici vom alege cel mai simplu criteriu de calcul. Vom minimiza media erorii pătrate:

Să scriem ultima expresie:

Dovada

Din faptul că toate variabilele aleatoare incluse în expresia pentru sunt independente, rezultă că toți termenii „încrucișați” sunt egali cu zero:

Am folosit faptul că atunci formula de varianță pare mult mai simplă:.

Această expresie capătă o valoare minimă atunci când (echivalăm derivata cu zero):

Aici scriem deja o expresie pentru coeficientul Kalman cu indicele pasului, prin urmare subliniem că depinde de pasul de iterație.
Inlocuim valoarea optima obtinuta in expresia pentru, pe care am minimizat-o. Noi primim;

Sarcina noastră a fost îndeplinită. Avem o formulă iterativă pentru a calcula coeficientul Kalman.
Să rezumam cunoștințele noastre dobândite într-un singur cadru:

Exemplu

Cod Matlab

Curata tot; N = 100% număr de probe a = 0,1% accelerație sigmaPsi = 1 sigmaEta = 50; k = 1: N x = k x (1) = 0 z (1) = x (1) + normrnd (0, sigmaEta); pentru t = 1: (N-1) x (t + 1) = x (t) + a * t + normrnd (0, sigmaPsi); z (t + 1) = x (t + 1) + normrnd (0, sigmaEta); Sfârșit; % filtru kalman xOpt (1) = z (1); eOpt (1) = sigmaEta; pentru t = 1: (N-1) eOpt (t + 1) = sqrt ((sigmaEta ^ 2) * (eOpt (t) ^ 2 + sigmaPsi ^ 2) / (sigmaEta ^ 2 + eOpt (t) ^ 2 + sigmaPsi ^ 2)) K (t + 1) = (eOpt (t + 1)) ^ 2 / sigmaEta ^ 2 xOpt (t + 1) = (xOpt (t) + a * t) * (1-K (t) +1)) + K (t + 1) * z (t + 1) capăt; grafic (k, xOpt, k, z, k, x)

Analiză

Dacă urmărim cum se modifică coeficientul Kalman odată cu pasul de iterație, se poate demonstra că se stabilizează întotdeauna la o anumită valoare. De exemplu, atunci când erorile rms ale senzorului și ale modelului sunt legate între ele ca zece la unu, atunci graficul coeficientului Kalman în funcție de pasul de iterație arată astfel:

În exemplul următor, vom discuta despre modul în care acest lucru ne poate face viața mult mai ușoară.

Al doilea exemplu

În practică, se întâmplă adesea să nu știm nimic despre modelul fizic al ceea ce filtrăm. De exemplu, doriți să filtrați citirile de la accelerometrul preferat. Nu știi dinainte după ce lege intenționezi să rotești accelerometrul. Cele mai multe informații pe care le puteți obține este variația erorii senzorului. Într-o situație atât de dificilă, toată ignoranța asupra modelului de mișcare poate fi condusă într-o variabilă aleatoare:

Dar, sincer vorbind, un astfel de sistem nu satisface deloc condițiile pe care le-am impus variabilei aleatoare, deoarece acum toată fizica mișcării necunoscută nouă este ascunsă acolo și, prin urmare, nu putem spune că în diferite momente de timp modelul erorile sunt independente unele de altele și că valorile lor medii sunt zero. În acest caz, în general, teoria filtrului Kalman nu este aplicabilă. Însă, nu vom acorda atenție acestui fapt, ci, în mod prostesc, aplicăm tot colosul de formule, alegând coeficienții la ochi, astfel încât datele filtrate să arate drăguț.
Dar poți lua o cale diferită, mult mai simplă. După cum am văzut mai sus, coeficientul Kalman se stabilizează întotdeauna spre o valoare cu creștere. Prin urmare, în loc să alegem coeficienții și să găsim coeficientul Kalman folosind formule complexe, putem considera că acest coeficient este întotdeauna constant și selectam numai această constantă. Această presupunere nu strică aproape nimic. În primul rând, folosim deja ilegal teoria lui Kalman, iar în al doilea rând, coeficientul Kalman se stabilizează rapid la o constantă. Ca rezultat, totul va fi foarte simplificat. În general, nu avem nevoie de nicio formulă din teoria lui Kalman, trebuie doar să găsim o valoare acceptabilă și să o introducem în formula iterativă:

Următorul grafic prezintă date de la un senzor fictiv filtrat în două moduri diferite. Cu condiția să nu știm nimic despre fizica fenomenului. Prima cale este sinceră, cu toate formulele din teoria lui Kalman. Iar al doilea este simplificat, fără formule.

După cum putem vedea, metodele sunt aproape aceleași. O mică diferență se observă doar la început, când coeficientul Kalman nu s-a stabilizat încă.

Discuţie

După cum am văzut, ideea principală a filtrului Kalman este de a găsi un coeficient astfel încât valoarea filtrată

în medie, ar fi cel mai puțin diferit de valoarea reală a coordonatei. Putem vedea că valoarea filtrată este o funcție liniară a citirii senzorului și a valorii filtrate anterioare. Și valoarea filtrată anterioară este, la rândul său, o funcție liniară a citirii senzorului și a valorii filtrate anterioare. Și așa mai departe, până când lanțul se desfășoară complet. Adică, valoarea filtrată depinde de dintre toate citirile anterioare ale senzorului liniar:

Prin urmare, filtrul Kalman se numește filtru liniar.
Se poate dovedi că filtrul Kalman este cel mai bun dintre toate filtrele liniare. Cel mai bun în sensul că pătratul mediu al erorii filtrului este minim.

Caz multidimensional

Întreaga teorie a filtrului Kalman poate fi generalizată la cazul multidimensional. Formulele de acolo arată puțin mai înfricoșătoare, dar însăși ideea derivării lor este aceeași ca și în cazul unidimensional. Le puteți vedea în acest articol excelent: http://habrahabr.ru/post/140274/.
Și în acest minunat video este analizat un exemplu de utilizare a acestora.

Filtrele Wiener sunt cele mai potrivite pentru procesele de procesare sau secțiunile de procese în general (procesare în bloc). Pentru procesarea secvenţială, este necesară o estimare curentă a semnalului la fiecare ciclu de ceas, ţinând cont de informaţiile care intră în intrarea filtrului în timpul procesului de observare.

Cu filtrarea Wiener, fiecare eșantion de semnal nou ar necesita recalcularea tuturor greutăților filtrului. În prezent s-au răspândit filtrele adaptive, în care noile informații primite sunt folosite pentru a corecta continuu evaluarea semnalului efectuată anterior (urmărirea țintei în radar, sisteme de control automate în control etc.). De un interes deosebit sunt filtrele adaptive de tip recursiv cunoscut sub numele de filtru Kalman.

Aceste filtre sunt utilizate pe scară largă în buclele de control din sistemele automate de reglare și control. De acolo au apărut ei, dovadă fiind o terminologie atât de specifică folosită pentru a descrie munca lor ca spațiu de stat.

Una dintre principalele sarcini de rezolvat în practica calculului neuronal este obținerea de algoritmi rapizi și fiabili pentru învățarea rețelelor neuronale. În acest sens, poate fi util să folosiți filtre liniare în bucla de feedback. Deoarece algoritmii de antrenament sunt de natură iterativă, un astfel de filtru trebuie să fie un estimator recursiv secvenţial.

Problema de estimare a parametrilor

Una dintre problemele teoriei deciziilor statistice, de mare importanță practică, este problema estimării vectorilor de stare și a parametrilor sistemelor, care se formulează astfel. Să presupunem că este necesar să se estimeze valoarea parametrului vectorial $ X $, care este inaccesibil măsurării directe. În schimb, se măsoară un alt parametru $ Z $, în funcție de $ X $. Problema de estimare este de a răspunde la întrebarea: ce se poate spune despre $ X $, cunoscând $ Z $. În cazul general, procedura de evaluare optimă a vectorului $ X $ depinde de criteriul acceptat al calității evaluării.

De exemplu, abordarea bayesiană a problemei estimării parametrilor necesită informații complete a priori despre proprietățile probabilistice ale parametrului estimat, ceea ce este adesea imposibil. În aceste cazuri, se recurge la metoda celor mai mici pătrate (OLS), care necesită mult mai puține informații a priori.

Să luăm în considerare aplicarea MOL pentru cazul în care vectorul de observație $ Z $ este legat de vectorul de estimare a parametrilor $ X $ printr-un model liniar, iar observația conține zgomot $ V $ necorelat cu parametrul estimat:

$ Z = HX + V $, (1)

unde $ H $ este o matrice de transformare care descrie relația dintre mărimile observate și parametrii estimați.

Estimarea $ X $ care minimizează eroarea pătrată este scrisă după cum urmează:

$ X_ (оц) = (H ^ TR_V ^ (- 1) H) ^ (- 1) H ^ TR_V ^ (- 1) Z $, (2)

Să nu fie corelat zgomotul $ V $, în acest caz matricea $ R_V $ este doar matricea identității, iar ecuația pentru estimare devine mai simplă:

$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $, (3)

Scrierea sub formă de matrice economisește foarte mult hârtie, dar poate fi neobișnuit pentru unii. Următorul exemplu, preluat din monografia lui Yu. M. Korshunov, „Mathematical Foundations of Cybernetics”, ilustrează toate acestea.
Următorul circuit electric este disponibil:

Valorile observate în acest caz sunt citirile dispozitivelor $ A_1 = 1 A, A_2 = 2 A, V = 20 B $.

În plus, este cunoscută rezistența $ R = 5 $ Ohm. Este necesar să se estimeze în cel mai bun mod, din punctul de vedere al criteriului pătratului mediu minim al erorii, valorile curenților $ I_1 $ și $ I_2 $. Cel mai important lucru aici este că există o relație între valorile observate (citirile instrumentului) și parametrii estimați. Și această informație este adusă din exterior.

În acest caz, acestea sunt legile lui Kirchhoff, în cazul filtrării (despre care vom discuta în continuare) - un model autoregresiv al unei serii de timp, care presupune dependența valorii curente față de cele precedente.

Deci, cunoașterea legilor lui Kirchhoff, care nu are nimic de-a face cu teoria deciziilor statistice, face posibilă stabilirea unei legături între valorile observate și parametrii estimați (cine a studiat ingineria electrică - pot verifica, restul va avea să se creadă pe cuvânt):

$$ z_1 = A_1 = I_1 + \ xi_1 = 1 $$

$$ z_2 = A_2 = I_1 + I_2 + \ xi_2 = 2 $$

$$ z_2 = V / R = I_1 + 2 * I_2 + \ xi_3 = 4 $$

Este sub formă vectorială:

$$ \ begin (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ begin (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) \ begin (vmatrix) I_1 \ \ I_2 \ end (vmatrix) + \ begin (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

Sau $ Z = HX + V $, unde

$$ Z = \ begin (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ begin (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix); H = \ begin (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix); X = \ begin (vmatrix) I_1 \\ I_2 \ end (vmatrix); V = \ begin (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

Având în vedere valorile interferenței necorelate între ele, găsim estimarea lui I 1 și I 2 prin metoda celor mai mici pătrate în conformitate cu formula 3:

$ H ^ TH = \ begin (vmatrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatrix) \ begin (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) = \ begin (vmatrix) 3 & 3 \\ 3 & 5 \ end (vmatrix); (H ^ TH) ^ (- 1) = \ frac (1) (6) \ begin (vmatrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) $;

$ H ^ TZ = \ begin (vmatrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatrix) \ begin (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix) = \ begin (vmatrix) 7 \ \ 10 \ end (vmatrix); X (ots) = \ frac (1) (6) \ begin (vmatrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) \ begin (vmatrix) 7 \\ 10 \ end (vmatrix) = \ frac (1) (6) \ begin (vmatrix) 5 \\ 9 \ end (vmatrix) $;

Deci $ I_1 = 5/6 = 0,833 A $; $ I_2 = 9/6 = 1,5 A $.

Sarcina de filtrare

Spre deosebire de problema estimării parametrilor, care au valori fixe, în problema filtrării se impune estimarea proceselor, adică găsirea estimărilor curente ale unui semnal care se modifică în timp, distorsionat de zgomot, și, prin urmare, , este inaccesibil la măsurarea directă. În general, tipul de algoritmi de filtrare depinde de proprietățile statistice ale semnalului și ale zgomotului.

Vom presupune că semnalul util este o funcție de timp care variază lent, iar interferența este un zgomot necorelat. Vom folosi metoda celor mai mici pătrate, din nou din cauza lipsei de informații a priori despre caracteristicile probabilistice ale semnalului și interferenței.

În primul rând, obținem o estimare a valorii curente de $ x_n $ pe baza $ k $ disponibile a celor mai recente valori ale seriei de timp $ z_n, z_ (n-1), z_ (n-2) \ puncte z_ (n- (k-1)) $. Modelul de observație este același ca în problema de estimare a parametrilor:

Este clar că $ Z $ este un vector coloană format din valorile observate ale seriei de timp $ z_n, z_ (n-1), z_ (n-2) \ puncte z_ (n- (k-1)) $, $ V $ - vector-coloană de zgomot $ \ xi _n, \ xi _ (n-1), \ xi_ (n-2) \ puncte \ xi_ (n- (k-1)) $, deformând adevăratul semnal. Ce înseamnă simbolurile $ H $ și $ X $? Despre ce, de exemplu, vectorul coloană $ X $ putem vorbi dacă tot ceea ce este necesar este să oferim o estimare a valorii curente a seriei temporale? Și ce se înțelege prin matricea de transformare $ H $ nu este deloc clar.

La toate aceste întrebări se poate răspunde numai dacă este introdus în considerare conceptul de model de generare a semnalului. Adică, este nevoie de un model al semnalului original. Acest lucru este de înțeles, în absența informațiilor a priori despre caracteristicile probabilistice ale semnalului și interferenței, nu mai rămâne decât să facem presupuneri. Puteți numi asta o ghicitoare pentru zațul de cafea, dar experții preferă o terminologie diferită. Pe „uscătorul de păr” lor se numește model parametric.

În acest caz, parametrii acestui model particular sunt estimați. Atunci când alegeți un model adecvat de generare a semnalului, amintiți-vă că orice funcție analitică poate fi extinsă într-o serie Taylor. O proprietate uimitoare a seriei Taylor este că forma unei funcții la orice distanță finită $ t $ dintr-un punct $ x = a $ este determinată în mod unic de comportamentul funcției într-o vecinătate infinit de mică a punctului $ x = a $ (vorbim despre derivatele sale de ordinul întâi și superior).

Astfel, existența seriei Taylor înseamnă că funcția analitică are o structură internă cu un cuplaj foarte puternic. Dacă, de exemplu, ne limităm la trei membri ai seriei Taylor, atunci modelul de generare a semnalului va arăta astfel:

$ x_ (n-i) = F _ (- i) x_n $, (4)

$$ X_n = \ begin (vmatrix) x_n \\ x "_n \\ x" "_ n \ end (vmatrix); F _ (- i) = \ begin (vmatrix) 1 & -i & i ^ 2/2 \\ 0 & 1 & -i \\ 0 & 0 & 1 \ end (vmatrix) $$

Adică, formula 4, pentru o ordine dată a polinomului (în exemplu, este 2) stabilește o legătură între valoarea $ n $ -a a semnalului din secvența de timp și $ (n-i) $ -th. Astfel, vectorul de stare estimat în acest caz include, în plus față de valoarea estimată reală, derivatele întâi și a doua ale semnalului.

În teoria controlului automat, un astfel de filtru ar fi numit filtru de ordinul 2 pentru astatism. Matricea de transformare $ H $ pentru acest caz (estimarea este efectuată pe baza eșantioanelor curente și $ k-1 $ anterioare) arată astfel:

$$ H = \ începe (vmatrix) 1 & -k & k ^ 2/2 \\ - & - & - \\ 1 & -2 & 2 \\ 1 & -1 & 0,5 \\ 1 & 0 & 0 \ sfârşitul (vmatrix) $$

Toate aceste numere sunt obținute din seria Taylor presupunând că intervalul de timp dintre valorile adiacente observate este constant și egal cu 1.

Deci, sarcina de filtrare conform ipotezelor noastre a fost redusă la sarcina de a estima parametrii; în acest caz se estimează parametrii modelului de generare a semnalului adoptat. Și estimarea valorilor vectorului de stat $ X $ se efectuează conform aceleiași formule 3:

$$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $$

În esență, am implementat un proces de estimare parametrică bazat pe un model autoregresiv al procesului de generare a semnalului.

Formula 3 poate fi implementată cu ușurință programatic, pentru aceasta trebuie să completați matricea $ H $ și coloana vectorială de observații $ Z $. Aceste filtre sunt numite filtre cu memorie finită, deoarece folosesc ultimele $ k $ observații pentru a obține estimarea curentă a $ X_ (nоц) $. La fiecare nou ciclu de observație, se adaugă unul nou la setul curent de observații, iar cel vechi este eliminat. Acest proces de obținere a notelor se numește fereastra glisanta.

Creșterea filtrelor de memorie

Filtrele cu memorie finită au principalul dezavantaj că după fiecare nouă observație este necesară reefectuarea unei recalculări complete a tuturor datelor stocate în memorie. În plus, calculul estimărilor poate fi început numai după ce au fost acumulate rezultatele primelor observații $ k $. Adică aceste filtre au un timp tranzitoriu lung.

Pentru a combate acest dezavantaj, este necesar să treceți de la un filtru de memorie persistent la un filtru cu memorie în creștere... Într-un astfel de filtru, numărul de valori observate pentru care se face estimarea trebuie să coincidă cu numărul n al observației curente. Aceasta face posibilă obținerea estimărilor pornind de la numărul de observații egal cu numărul de componente ale vectorului estimat $ X $. Și aceasta este determinată de ordinea modelului adoptat, adică câți termeni din seria Taylor sunt folosiți în model.

În același timp, odată cu creșterea n, proprietățile de netezire ale filtrului se îmbunătățesc, adică acuratețea estimărilor crește. Cu toate acestea, implementarea directă a acestei abordări este asociată cu o creștere a costurilor de calcul. Prin urmare, filtrele de memorie în creștere sunt implementate ca recurent.

Cert este că până în momentul n avem deja o estimare $ X _ ((n-1) оц) $, care conține informații despre toate observațiile anterioare $ z_n, z_ (n-1), z_ (n-2) \ puncte z_ (n- (k-1)) $. Estimarea $ X_ (nоц) $ se obține din următoarea observație $ z_n $ folosind informațiile stocate în estimarea $ X _ ((n-1)) (\ mbox (оц)) $. Această procedură se numește filtrare recurentă și constă în următoarele:

• conform estimării $ X _ ((n-1)) (\ mbox (оц)) $ prezice estimarea $ X_n $ conform formulei 4 cu $ i = 1 $: $ X _ (\ mbox (nоtsapriori)) = F_1X _ ((n-1 ) sc) $. Aceasta este o estimare a priori;
• conform rezultatelor observaţiei curente $ z_n $, această estimare a priori se transformă într-una adevărată, adică a posteriori;
• această procedură se repetă la fiecare pas, începând de la $ r + 1 $, unde $ r $ este ordinea de filtrare.

Formula finală pentru filtrarea recurentă arată astfel:

$ X _ ((n-1) оц) = X _ (\ mbox (nоtsapriori)) + (H ^ T_nH_n) ^ (- 1) h ^ T_0 (z_n - h_0 X _ (\ mbox (nоtsapriori))) $ , (6 )

unde pentru filtrul nostru de a doua comandă:

Un filtru de memorie în creștere bazat pe Formula 6 este un caz special al unui algoritm de filtrare cunoscut sub numele de filtru Kalman.

În implementarea practică a acestei formule, trebuie amintit că estimarea a priori inclusă în ea este determinată de formula 4, iar valoarea $ h_0 X _ (\ mbox (notspriori)) $ este prima componentă a vectorului $ X _ (\ mbox (notspriori)) $.

Filtrul de memorie în creștere are o caracteristică importantă. Dacă te uiți la formula 6, atunci scorul final este suma vectorului de scor prezis și a termenului corector. Această corecție este mare pentru $ n $ mici și scade odată cu creșterea $ n $, tinzând spre zero ca $ n \ rightarrow \ infty $. Adică, odată cu creșterea lui n, proprietățile de netezire ale filtrului cresc și modelul inerent acestuia începe să domine. Dar semnalul real poate corespunde modelului numai în anumite zone, prin urmare, precizia prognozei se deteriorează.

Pentru a combate acest lucru, pornind de la niște $ n $, se impune o interdicție privind reducerea în continuare a termenului de corecție. Acest lucru este echivalent cu schimbarea lățimii de bandă a filtrului, adică pentru n mic filtrul este mai larg (mai puțin inerțial), pentru n mare devine mai inerțial.

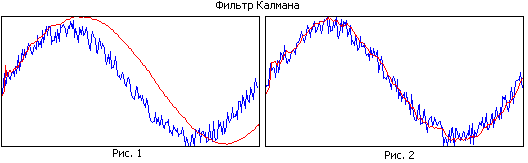
Comparați Figura 1 și Figura 2. În prima figură, filtrul are o memorie mare, în timp ce se netezește bine, dar din cauza benzii înguste, traiectoria estimată rămâne în urmă cu cea reală. În a doua figură, memoria filtrului este mai mică, se netezește mai rău, dar urmează mai bine traiectoria reală.

Literatură

1. YM Korshunov „Bazele matematice ale ciberneticii”
2. A.V. Balakrishnan „Teoria filtrării Kalman”
3. VNFomin „Estimarea recurentă și filtrarea adaptivă”
4. C.F.N. Cowen, P.M. Acordați „Filtre adaptive”

Acest filtru este utilizat în diverse domenii - de la inginerie radio până la economie. Aici vom discuta despre ideea principală, sensul, esența acestui filtru. Va fi prezentat în cel mai simplu mod posibil.
Să presupunem că avem nevoie de a măsura unele cantități ale unui obiect. În inginerie radio, cel mai adesea se ocupă de măsurători ale tensiunilor la ieșirea unui anumit dispozitiv (senzor, antenă etc.). În exemplul cu un electrocardiograf (vezi) avem de-a face cu măsurători ale biopotențialelor pe corpul uman. În economie, de exemplu, valoarea măsurată poate fi cursul de schimb. În fiecare zi cursul de schimb este diferit, adică în fiecare zi „măsurătorile lui” ne dau o valoare diferită. Și dacă să generalizăm, atunci putem spune că cea mai mare parte a activității unei persoane (dacă nu toată) se reduce tocmai la măsurători-comparații constante ale anumitor cantități (vezi cartea).
Deci, să presupunem că măsurăm constant ceva. Să presupunem, de asemenea, că măsurătorile noastre vin întotdeauna cu o eroare - acest lucru este de înțeles, deoarece nu există instrumente de măsurare ideale și fiecare produce un rezultat cu o eroare. În cel mai simplu caz, ceea ce s-a descris se poate reduce la următoarea expresie: z = x + y, unde x este valoarea adevărată pe care dorim să o măsurăm și care ar fi măsurată dacă am avea un dispozitiv de măsurare ideal, y este eroarea de măsurare introdusă de dispozitivul de măsurare și z - valoarea pe care am măsurat-o. Așadar, sarcina filtrului Kalman este să ghicească (determină) din z-ul măsurat, dar care a fost valoarea adevărată a lui x când am primit z-ul nostru (în care valoarea adevărată și eroarea de măsurare „stau”). Este necesar să se filtreze (înlăturați) valoarea adevărată a lui x din z - eliminați zgomotul de distorsionare y din z. Adică, având la îndemână doar suma, trebuie să ghicim ce termeni au dat această sumă.
În lumina celor de mai sus, vom formula acum totul după cum urmează. Să presupunem că există doar două numere aleatorii. Ni se dă doar suma lor și ni se cere să stabilim prin această sumă care sunt termenii. De exemplu, ni s-a dat numărul 12 și ei spun: 12 este suma numerelor x și y, întrebarea este cu ce sunt x și y egali. Pentru a răspunde la această întrebare, compunem ecuația: x + y = 12. Am obținut o ecuație cu două necunoscute, prin urmare, strict vorbind, nu este posibil să găsim două numere care au dat această sumă. Dar mai putem spune ceva despre aceste cifre. Putem spune că au fost fie numerele 1 și 11, fie 2 și 10, fie 3 și 9, fie 4 și 8 etc., de asemenea, este fie 13 și -1, fie 14 și -2, fie 15 și - 3, etc. Adică prin suma (în exemplul nostru, 12), putem determina setul de opțiuni posibile care însumează exact 12. Una dintre aceste opțiuni este perechea pe care o căutăm, care de fapt a dat 12 chiar acum. De asemenea, merită remarcat faptul că toate variantele de perechi de numere care dau un total de 12 formează o linie dreaptă prezentată în Fig. 1, care este dată de ecuația x + y = 12 (y = -x + 12).

Fig. 1

Astfel, perechea pe care o căutăm se află undeva pe această linie dreaptă. Repet, este imposibil să alegi dintre toate aceste opțiuni perechea care a fost de fapt - care a dat cifra 12, fără a avea niciun indiciu suplimentar. Dar, în situația pentru care a fost inventat filtrul Kalman, există astfel de indicii... Se știe ceva despre numerele aleatoare dinainte. În special, așa-numita histogramă de distribuție pentru fiecare pereche de numere este cunoscută acolo. Se obține de obicei după o observare destul de lungă a apariției acestor numere foarte aleatorii. Adică, de exemplu, se știe din experiență că în 5% din cazuri o pereche x = 1, y = 8 cade de obicei (notăm această pereche ca: (1,8)), în 2% din cazuri o pereche. x = 2, y = 3 ( 2,3), în 1% din cazuri o pereche (3,1), în 0,024% din cazuri o pereche (11,1) etc. Din nou, această histogramă este setată pentru toate cuplurile numere, inclusiv cele care formează un total de 12. Astfel, pentru fiecare pereche, care dă un total de 12, putem spune că, de exemplu, o pereche (1, 11) iese în 0,8% din cazuri, o pereche ( 2, 10) - în 1% din cazuri, o pereche (3, 9) - în 1,5% din cazuri etc. Astfel, putem folosi histograma pentru a determina în ce procent din cazuri suma termenilor unei perechi este 12. Să presupunem, de exemplu, în 30% din cazuri suma este 12. Iar în restul de 70% perechile rămase cad out - acestea sunt (1,8), (2, 3), (3,1), etc. - cele care însumează alte numere decât 12. Și să cadă, de exemplu, o pereche (7,5) în 27% din cazuri, în timp ce toate celelalte perechi care însumează 12 cad în 0,024% + 0,8% + 1% + 1,5% +... = 3% din cazuri. Deci, conform histogramei, am aflat că numerele care dau un total de 12 cad în 30% din cazuri. În același timp, știm că dacă 12 a scăzut, atunci cel mai adesea (în 27% din 30%) motivul pentru aceasta este perechea (7,5). Adică dacă deja Cu 12 lansat, putem spune că în 90% (27% din 30% - sau, ceea ce este la fel de 27 de ori din 30), motivul unui 12 aruncat este o pereche (7,5). Știind că cel mai adesea motivul pentru a obține suma egală cu 12 este perechea (7,5), este logic să presupunem că, cel mai probabil, a căzut acum. Desigur, încă nu este un fapt că, de fapt, acum numărul 12 este format din această pereche specială, totuși, de data viitoare, dacă întâlnim 12 și presupunem din nou perechea (7,5), atunci undeva în 90% din cazuri din 100% vom avea dreptate. Dar dacă presupunem perechea (2, 10), atunci vom avea dreptate doar 1% din 30% din timp, ceea ce reprezintă 3,33% presupuneri corecte comparativ cu 90% dacă presupunem perechea (7,5). Asta e tot - acesta este punctul de vedere al algoritmului de filtru Kalman. Adică, filtrul Kalman nu garantează că nu va face o greșeală în determinarea sumandului, dar garantează că va greși de câte ori se va face o greșeală de câte ori (probabilitatea de eroare va fi minimă), deoarece folosește statistici - o histogramă a perechilor de numere lipsă. De asemenea, trebuie subliniat faptul că așa-numita densitate de distribuție a probabilității (PDF) este adesea folosită în algoritmul de filtrare Kalman. Cu toate acestea, trebuie să înțelegeți că sensul este același cu cel al histogramei. Mai mult, o histogramă este o funcție construită pe baza PDF-ului și este o aproximare a acesteia (vezi, de exemplu,).
În principiu, putem reprezenta această histogramă în funcție de două variabile - adică ca o suprafață deasupra planului xy. Acolo unde suprafața este mai mare, există o probabilitate mai mare de apariție a unei perechi corespunzătoare. Figura 2 prezintă o astfel de suprafață.

fig. 2

După cum puteți vedea mai sus, linia dreaptă x + y = 12 (care are opțiuni pentru perechi care oferă un total de 12) punctele de suprafață sunt situate la diferite înălțimi și cea mai mare înălțime pentru opțiunea cu coordonate (7,5). Iar când întâlnim o sumă egală cu 12, în 90% din cazuri motivul apariției acestei sume este tocmai perechea (7,5). Acestea. această pereche, dând un total de 12, este cea care are cea mai mare probabilitate de apariție, cu condiția ca totalul să fie 12.
Astfel, ideea din spatele filtrului Kalman este descrisă aici. Pe el sunt construite tot felul de modificări - într-un singur pas, recurent în mai multe etape etc. Pentru un studiu mai profund al filtrului Kalman, recomand cartea: Van Tries G. Theory of detection, estimation and modulation.

p.s. Pentru cei care sunt interesați să explice conceptele de matematică, ceea ce se numește „pe degete”, le puteți sfătui această carte și, în special, capitolele din secțiunea ei „Matematică” (puteți achiziționa cartea în sine sau capitole individuale de la aceasta).

Random Forest este unul dintre algoritmii mei preferați de extragere a datelor. În primul rând, este incredibil de versatil; poate fi folosit pentru a rezolva atât probleme de regresie, cât și de clasificare. Căutați anomalii și selectați predictori. În al doilea rând, acesta este un algoritm care este cu adevărat dificil de aplicat incorect. Pur și simplu pentru că, spre deosebire de alți algoritmi, are puțini parametri configurabili. De asemenea, este surprinzător de simplu la bază. Și, în același timp, este remarcabil prin precizie.

Care este ideea din spatele unui astfel de algoritm minunat? Ideea este simplă: să presupunem că avem un algoritm foarte slab, să zicem. Dacă facem o mulțime de modele diferite folosind acest algoritm slab și facem o medie a rezultatului predicțiilor lor, atunci rezultatul final va fi mult mai bun. Acesta este așa-numitul antrenament de ansamblu în acțiune. Algoritmul Random Forest se numește așadar „Random Forest”, pentru datele obținute creează mulți arbori de decizie și apoi face media rezultatului predicțiilor lor. Un punct important aici este elementul aleatoriu în crearea fiecărui copac. La urma urmei, este clar că, dacă creăm mulți copaci identici, atunci rezultatul medierii lor va avea acuratețea unui singur copac.

Cum lucrează? Să presupunem că avem niște date de intrare. Fiecare coloană corespunde unui parametru, fiecare rând corespunde unui element de date.

Putem selecta aleatoriu un anumit număr de coloane și rânduri din întregul set de date și putem construi un arbore de decizie pe baza acestora.

joi, 10 mai 2012

joi, 12 ianuarie 2012

Asta e tot. Zborul de 17 ore s-a încheiat, Rusia a rămas peste ocean. Iar prin fereastra unui apartament confortabil cu 2 dormitoare San Francisco, faimoasa Silicon Valley, California, SUA se uită la noi. Da, tocmai acesta este motivul pentru care practic nu am scris în ultima vreme. Ne-am mutat.

Totul a început în aprilie 2011, când făceam un interviu telefonic la Zynga. Apoi totul mi s-a părut un fel de joc care nu avea nimic de-a face cu realitatea și nici nu mi-am putut imagina în ce va rezulta. În iunie 2011, Zynga a venit la Moscova și a realizat o serie de interviuri, au fost luați în considerare aproximativ 60 de candidați care au promovat interviurile telefonice și au fost selectați aproximativ 15 dintre ei (nu știu numărul exact, cineva s-a răzgândit ulterior, cineva imediat refuzat). Interviul s-a dovedit a fi surprinzător de simplu. Nu a fost testată nicio sarcină de programare, nicio întrebare dificilă cu privire la forma trapelor, mai ales capacitatea de a discuta. Iar cunoștințele, după părerea mea, au fost evaluate doar superficial.

Și atunci a început trucul. În primul rând, am așteptat rezultatele, apoi oferta, apoi aprobarea LCA, apoi aprobarea petiției pentru viză, apoi documentele din SUA, apoi coada la ambasada, apoi un control suplimentar, apoi Visa. Uneori mi se părea că sunt gata să renunț la totul și să marchez. Uneori mă îndoiam dacă avem nevoie de această America, la urma urmei, nici în Rusia nu este rău. Întregul proces a durat aproximativ șase luni, drept urmare, la jumătatea lunii decembrie am primit vize și am început să ne pregătim pentru plecare.

Luni a fost prima mea zi la serviciu. Biroul are toate condițiile nu numai pentru a lucra, ci și a locui. Mic dejun, prânz și cine de la bucătarii noștri, o grămadă de mâncare variată înghesuită peste tot, o sală de sport, masaj și chiar un coafor. Toate acestea sunt complet gratuite pentru angajați. Mulți oameni ajung la muncă cu bicicleta și există mai multe încăperi pentru depozitarea vehiculelor. În general, nu am întâlnit niciodată așa ceva în Rusia. Totul, însă, are propriul preț, am fost imediat avertizați că va trebui să muncim mult. Ce este „mult”, după standardele lor, nu îmi este foarte clar.

Sper totuși că, în ciuda volumului de muncă, voi putea relua bloggingul în viitorul apropiat și poate să vă spun ceva despre viața și munca americană ca programator în America. Așteaptă și vezi. Între timp, îi felicit pe toți pentru Anul Nou și Crăciunul care vin și ne vedem curând!

Pentru un exemplu de utilizare, vom tipări randamentul dividendelor companiilor rusești. Ca preț de bază, luăm prețul de închidere al unei acțiuni în ziua închiderii registrului. Din anumite motive, aceste informații nu se află pe site-ul troicii, dar sunt mult mai interesante decât valorile absolute ale dividendelor.
Atenţie! Executarea codului durează mult, deoarece pentru fiecare promoție, trebuie să faceți o cerere către serverele finam și să obțineți valoarea acesteia.

Rezultat<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0) (încercați ((ghilimele<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0) (dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

În mod similar, puteți construi statistici pentru anii trecuți.

Cumva s-a întâmplat că îmi plac foarte mult tot felul de algoritmi care au o justificare matematică clară și logică) Dar adesea descrierea lor pe Internet este atât de supraîncărcată cu formule și calcule încât este pur și simplu imposibil de înțeles sensul general al algoritmului. Dar înțelegerea esenței și principiului de funcționare a unui dispozitiv / mecanism / algoritm este mult mai importantă decât memorarea unor formule uriașe. Oricât de banal ar fi, memorarea chiar și a sutelor de formule nu va ajuta la nimic dacă nu știi cum și unde să le aplici 😉 De fapt, pentru ce sunt toate acestea .. Am decis să încurc descrierea unor algoritmi cu care trebuia să mă ocup cu în practică. Voi încerca să nu mă supraîncărc cu calcule matematice, astfel încât materialul să fie clar și lectura ușoară.

Și astăzi vom vorbi despre filtru Kalman, să ne dăm seama ce este, de ce și cum se folosește.

Să începem cu un mic exemplu. Să ne confruntăm cu sarcina de a determina coordonatele unui avion zburător. Mai mult, desigur, coordonatele (să o desemnăm) ar trebui determinată cât mai precis posibil.

În avion, am preinstalat un senzor, care ne oferă datele de locație dorite, dar, ca tot pe lumea asta, senzorul nostru nu este perfect. Prin urmare, în loc de o valoare, obținem:

unde este eroarea senzorului, adică o variabilă aleatorie. Astfel, din citirile inexacte ale aparaturii de masura, trebuie sa obtinem valoarea coordonatei () cat mai aproape de pozitia reala a aeronavei.

Problema este pusă, să trecem la rezolvarea ei.

Anunțați-ne acțiunea de control (), datorită căreia zboară avionul (pilotul ne-a spus ce pârghii trage 😉). Apoi, cunoscând coordonatele la pasul k, putem obține valoarea la pasul (k + 1):

S-ar părea că de asta ai nevoie! Și nu este nevoie de filtru Kalman aici. Dar nu totul este atât de simplu.. În realitate, nu putem lua în considerare toți factorii externi care afectează zborul, așa că formula ia următoarea formă:

unde este o eroare cauzată de influențe externe, imperfecțiunea motorului etc.

Deci ce se întâmplă? La pasul (k + 1), avem, în primul rând, o citire inexactă a senzorului și, în al doilea rând, o valoare calculată incorect, obținută din valoarea din pasul anterior.

Ideea filtrului Kalman este de a obține o estimare exactă a coordonatei dorite (pentru cazul nostru) din două valori imprecise (luându-le cu coeficienți de greutate diferiți). În general, valoarea măsurată poate fi absolut orice (temperatură, viteză..). Iată ce se întâmplă:

Prin calcule matematice, putem obține o formulă de calcul a coeficientului Kalman la fiecare pas, dar, așa cum sa convenit la începutul articolului, nu vom aprofunda în calcule, mai ales că s-a stabilit în practică că coeficientul Kalman întotdeauna tinde spre o anumită valoare cu creșterea k. Obținem prima simplificare a formulei noastre:

Acum să presupunem că nu există nicio comunicare cu pilotul și nu cunoaștem acțiunea de control. S-ar părea că în acest caz nu putem folosi filtrul Kalman, dar nu este așa 😉 Pur și simplu „aruncăm” din formulă ceea ce nu știm, atunci

Obținem cea mai simplificată formulă a lui Kalman, care totuși, în ciuda unor astfel de simplificări „grele”, își face față perfect sarcinii. Dacă reprezentați rezultatele grafic, obțineți ceva de genul următor:

Dacă senzorul nostru este foarte precis, atunci, în mod natural, factorul de ponderare K ar trebui să fie aproape de unu. Dacă situația este inversă, adică senzorul nostru nu este foarte bun, atunci K ar trebui să fie mai aproape de zero.

Probabil asta e tot, așa tocmai ne-am dat seama de algoritmul de filtrare Kalman! Sper că articolul a fost util și clar =)