Лінійна залежність базис розмірність заміна базису. Існування базису векторного простору Доповнити базис підпростору до базису всього простору
Визначення. Система елементів хь ..., хч лінійного простору V називається лінійно залежною, якщо знайдуться числа а », ..., otq, не всі рівні нулю і такі, що Якщо рівність (1) виконується тільки при а] \u003d ... \u003d aq \u003d 0, то система елементів xj ,. .., х9 називається лінійно незалежною. Справедливі наступні твердження. Теорема 1. Система елементів Х \\, ..., xq (q ^ 2) лінійно залежна в тому і тільки в тому випадку, якщо хоча б один з її елементів можна представити у вигляді лінійної комбінації інших. Припустимо спочатку, що система елементів хь ..., xq лінійно залежна. Будемо вважати для визначеності, що в рівності (1) відмінний від нуля коефіцієнт а9. Переносячи всі складові, крім останнього, в праву частину, після поділу на otq Ф Про отримаємо, що елементxq є лінійною комбінацією елементів xi, ..., xq: Назад, якщо один з елементів дорівнює лінійної комбінації інших, то, переносячи його в ліву частина, отримаємо лінійну комбінацію в якій є відмінні від нуля коефіцієнти (-1 Ф 0). Значить, система елементів Xi, _____ xq лінійно залежна. Теорема 2. Нехай система елементів Х |, ..., Х9 лінійно незалежна і у \u003d а \\ Х \\ +. + Aqxq. Тоді коефіцієнти ori, ..., aq визначаються по елементу у єдиний образ. м Нехай Тоді Лінійна залежність Базис Розмірність Заміна базису звідки. з лінійної незалежності елементів Х |, ..., xq випливає, що а (і, отже, а Теорема 3. Система елементів, що містить лінійно залежну підсистему, лінійно залежна. "Нехай перші q елементів системи хь ..., xq, xg + l, ..., хт лінійно залежні. Тоді знайдеться лінійна комбінація цих елементів така, що й не всі коефіцієнти від ", ..., aq дорівнюють нулю. Додаючи елементи, ..., хт з нульовими множителями, отримуємо, що і в лінійній комбінації рис-5 дорівнюють нулю не всі коефіцієнти. Приклад. Вектори з Vj лінійно залежні тоді і тільки тоді, коли вони компланарні (рис.5). Упорядкована система елементів в |, ..., е "лінійного простору V називається базисом цього лінійного простору, якщо елементи в |, ..., єп лінійно незалежні і кожен елемент з V можна представити у вигляді їх лінійної комбінації. Упорядкованість означає тут, що кожному елементу приписаний певний (порядковий) номер. з однієї системи п елементів можна побудувати п! упорядкованих систем. Приклад, Нехай а.Ь.с - трійка некомпланарних векторів з V j (рис.6). Тоді впорядковані трійки - різні базиси Нехай з \u003d (в! ... єп) - базис простору V. Тоді для будь-якого елемента х з V знайдеться набір чисел ..., З такою, що В силу теореми 2 числа, ..., с - координати елемента х в базисі з - визначені однозначно. Подивимося, що відбувається з координатами елементів при простейшіхдействіях зніми. Нехай і дл я будь-якого числа а Таким чином, при складанні елементів їх відповідні координати складаються, а при множенні елемента на число все його координати множаться на це число. Координати елементачасто зручно записувати у вигляді стовпчика. Наприклад, п - координатний стовпець елемента в базисі с. Розкладемо довільну систему елементів Х |, ..., х, по базису с, і розглянемо координатні стовпчики елементів Х |, ..., х9 в цьому базисі: Теорема 4. Система елементів х \\, ..., xq лінійно залежна тоді і тільки тоді, коли лінійно залежна система їх координатних стовпчиків в якомусь базисі. * Нехай причому хоча б один з коефіцієнтів А * відмінний від нуля. Запишемо це докладніше Звідси в силу єдиності розкладання елемента по базису випливає, що Лінійна залежність Базис Розмірність Заміна базису Таким чином, лінійна комбінація координатних стовпців елементів xt, ..., xq дорівнює нульовому стовпцю (з тими ж коефіцієнтами А |, ..., А?). Це і означає, що система координатних стовпців лінійно залежна. Якщо ж виконується рівність (2), то, проводячи міркування в зворотному порядку, отримуємо формулу (1). Тим самим, звернення в нуль деякої нетривіальною (хоча б один з коефіцієнтів відмінний від нуля) лінійної комбінації елементів лінійного простору рівнозначно тому, що нетривіальна лінійна комбінація їх координатних стовпчиків (з тими ж коефіцієнтами) дорівнює нульовому стовпцю. Теорема 5. Нехай базис з лінійного простору V складається з п елементів. Тоді будь-яка система з т елементів, де т\u003e п, лінійно залежна. або, що теж, * В силу теореми 3 досить розглянути випадок Нехай Xj, ..., хп + | - довільні елементи простору V. Розкладемо кожен елемент по базису з і запишемо координати елементів ........... у вигляді матриці, відводячи стовпець координатам елемента. Отримаємо матрицю з п рядків ип + 1 стовпців - З огляду на те, що ранг матриці К не перевищує числа п її рядків, стовпці матриці К (їх п + 1) лінійно залежні. А так як це координатні стовпчики елементів, то відповідно до теореми 4 система елементів Х | ..... х "+ | також лінійно залежна. Слідство. Все базиси лінійного простору V складаються з однакового чіиа елементів. Нехай базис з складається з п елементів, а базис з "з п елементів. В силу тільки що доведеної теореми з лінійної незалежності системи е \\, ..., е" п робимо висновок, що п "^ п. Змінюючи базиси е і з" місцями, в силу цієї ж теореми одержуємо, що п ^ п ". Тим самим, п \u003d п. Лшкрность / олінейногопространства V називається число елементів базису цього простору. Приклад 1. Базис координатного простору Еп утворюють елементи 4 Система елементів ei.ej ,. .., єп лінійно незалежна: з рівності отримуємо, що і означає, Крім того, будь-який елемент Е, \u003d ... з R "можна записати у вигляді лінійної комбінації елементів Тим самим, розмірність простору R дорівнює п. Приклад 2. Однорідна лінійна система має ненульові рішення, володіє фундаментальною системою рішень (ФСР). ФСР є базисом лінійного простору рішень однорідної системи. Розмірність цього лінійного простору дорівнює числу елементів ФСР, тобто п - р де г - ранг матриці коефіцієнтів однорідної системи, an - число невідомих. Приклад 3. Розмірність лінійного простору Мп многочленів ступеня не вище п дорівнює п + 1. 4 Так як всякий многочлен / * (() ступеня не вище п має вигляд то досить показати лінійну незалежність елементів в | \u003d. Розглянемо рівність де t довільно. Вважаючи t \u003d 0, отримуємо, що «о \u003d 0. 5 Зак.750 Продифференцируем рівність (3) по t: Знову покласти t \u003d 0, отримаємо, щО 0 | \u003d 0. Продовжуючи цей процес, послідовно переконуємося в тому, що оо \u003d «I \u003d ... \u003d а" \u003d 0. Це. означає, що система елементів в | \u003d 1, ..., ЕП4) \u003d * п лінійно незалежна. Отже, шукана розмірність дорівнює п + 1. Угоду. Далі в цій главі всюди вважається, якщо не визначено інше, що розмірність лінійного простору V рівна. Ясно, що якщо W - підпростір n-мірного лінійного простору V, то dim W ^ п. Покажемо, що в п-вимірному лінійному просторі V є лінійні підпростори будь-якої розмірності до ^ п. Нехай з \u003d - базис простору V. Легко переконатися втому, чтолінейная оболонка має розмірність к. За визначенням Теорема б (про поповнення базису). Пустьсістема елементів лінійного простору V розмірності п лінійно незалежна і к. Тоді в просторі V знайдуться елементи а * + 1, ..., ап такі, що система а "- базис V. М Нехай b - довільний елемент лінійного простору V. Якщо система лінійно залежна, то ^ так як в нетривіальною лінійної комбінації коефіцієнт внаслідок лінійної незалежності системи a Якби розкладання виду (4) можна було б написати для будь-якого елемента b простору V, то вихідна система а |, ..., а * була б базисом згідно з визначенням. Але в силу умови це неможливо. Тому повинен існувати елемент a * + i € V такий, що поповнена система ai, ..., аь, а * + | буде л іній але незалежною. Якщо до + 1 \u003d п, то ця система - базис простору V. Якщо до + 1, то для системи a слід повторити попередні міркування. Таким способом будь-яку задану лінійно незалежну систему елементів можна добудувати до базису всього простору V. Приклад. Доповнити систему з двох векторів а | \u003d (1,2,0,1), aj \u003d (-1,1.1,0) простору R4 до базису цього простору. М Візьмемо в просторі R4 вектори aj \u003d (і покажемо, що система векторів ai.aj.aj, а4 - базис R4. Ранг матриці рядками якої є координати векторів ААГ, аз, Е4, дорівнює чотирьом. Це означає, що рядки матриці А, а, значить, і вектори at. аг. аз, а ^ лінійно незалежні.\u003e Подібний підхід використовується і в загальному випадку: щоб доповнити систему до лінійно незалежних елементів до базису простору, матриця Лінійна залежність Базис Розмірність Заміна базису елементарними перетвореннями рядків приводиться до трапецієподібної формі, а потім доповнюється п - до рядками виду так, щоб ранг одержуваної матриці дорівнював п. Справедливо наступне твердження. Теорема 7. Нехай - лінійні підпростори лінійного простору V, Тоді. Заміна базису Нехай - базиси лінійного простору V. Розкладемо елементи базису з по базису с. Маємо Ці співвідношення зручно записати в матричної формі Матриця називається матрицею переходу від базису з базису з ". Властивості матриці переходу Доказ пов ого властивості проводиться від противного. З рівності det S \u003d 0 випливає лінійна залежність стовпців матриці S. Ці стовпці є координатними стовпчиками елементове ", ...» е "п в базисі с. Тому (і внаслідок теореми 4) елементи е "і ..., е" п повинні бути лінійно залежними. Останнє суперечить тому, що з "- базис. Значить, припущення, що det S \u003d 0, невірно. 2. Якщо ..., і ..., - координати елемента х в базисах з і з" відповідно, то _ Замінюючи в формулою їх виразами (1), отримуємо, що звідси в силу єдиності розкладання елемента по базису маємо I Переходячи до матричної записи знайдених рівності, переконуємося в справедливості властивості 2. 3. S-1 - матриця переходу від базису з "до базису с.
нехай V векторний простір над полем Р, S - система векторів з V.
Визначення 1. Базисом системи векторів S називається така впорядкована лінійно незалежна підсистема B 1, B 2, ..., B R системи S, Що будь-який вектор системи S лінійна комбінація векторів B 1, B 2, ..., B R.
Визначення 2. Рангом системи векторів S називається число векторів базису системи S. Позначається ранг системи векторів S символом R \u003d rang S.
Якщо S \u003d ( 0 ), То система не має базису і передбачається, що rang S= 0.
Приклад 1. Нехай дана система векторів A 1 = (1,2), A 2 = (2,3), A 3 = (3,5), A 4 \u003d (1,3). вектора A 1 , A 2 утворюють базис даної системи, так як вони лінійно незалежні (див. Приклад 3.1) і A 3 = A 1 + A 2 , A 4 = 3A 1 - A 2. Ранг даної системи векторів дорівнює двом.
теорема 1 (Теорема про базисах). Нехай S - кінцева система векторів з V, S ≠{0 }. Тоді справедливі твердження.
1 ° Будь-яку лінійно незалежну підсистему системи S можна доповнити до базису.
2 ° Система S володіє базисом.
2 ° Будь-які два базису системи S містять однакове число векторів, т. Е. Ранг системи не залежить від вибору базису.
4 ° якщо R \u003d rang S, то будь-які r лінійно незалежних векторів утворюють базис системи S.
5 ° якщо R \u003d rang S, То будь-які k\u003e r векторів системи S лінійно залежні.
6 ° будь-вектор A € S єдиним чином лінійно виражається через вектори базису, т. Е., Якщо B1, B2, ..., BR базис системи S, то
A = A1 B 1 + A2 B 2 +...+ ARB R; A1 , A2 , ..., AN € P,(1)
І таке уявлення єдино.
В силу 5 ° базис це Максимально лінійно незалежна підсистема системи S, А ранг системи S число векторів в такий підсистемі.
подання вектора A у вигляді (1) називається Розкладанням вектора по векторах базису, А числа a1, a2 , ..., ar називаються координатами вектора A В даному базисі.
Доведення. 1 ° Хай B 1, B 2, ..., B K - лінійно незалежна підсистема системи S. Якщо кожен вектор системи SЛінійно виражається через вектори нашої підсистеми, то за визначенням вона є базисом системи S.
Якщо є вектор в системі S , Який лінійно не виражає через вектора B 1, B 2, ..., B K, То позначимо його через B K+1. тоді системи B 1, B 2, ..., B K, B K+1 - лінійно незалежна. Якщо кожен вектор системи SЛінійно виражається через вектори цієї підсистеми, то за визначенням вона є базисом системи S.
Якщо є вектор в системі S , Який лінійно не виражає через B 1, B 2, ..., B K, B K+1, то повторимо міркування. Продовжуючи цей процес, ми або прийдемо до базису системи S, Або збільшимо число векторів в лінійно незалежної системи на одиницю. Так як в системі S кінцеве число векторів, то друга альтернатива не може тривати нескінченно і на певному етапі отримаємо базис системи S.
2 ° Нехай S кінцева система векторів і S ≠{0 ). Тоді в системі S є вектор B 1 ≠ 0, який утворює лінійно незалежну підсистему системи S . По першій частині його можна доповнити до базису системи S . Таким чином система S володіє базисом.
3 ° Припустимо, що система S має два базису:
B 1, B 2, ..., B R , (2)
C 1, C 2, ..., C S , (3)
За визначенням базису система векторів (2) лінійно незалежна і (2) Í S . Далі за визначенням базису кожен вектор системи (2) лінійна комбінація векторів системи (3). Тоді по основній теоремі про двох системах векторів R £ S. Аналогічно доказавается, що S £ R. З цих двох нерівностей слід R = S.
4 ° Нехай R \u003d rang S, A 1, A 2, ..., A R - лінійно незалежна підсистема S. Покажемо, що вона є базисом систем S. Якщо вона не є базисом, то по першій частині її можна доповнити до базису і отримаємо базис A 1, A 2, ..., A R, A R+1,..., A R+T , Що містить більш ніж R
5 ° Якщо K векторів A 1, A 2, ..., A K (K > R) системи S - лінійно незалежні, то по першій частині цю систему векторів можна доповнити до базису і отримаємо базис A 1, A 2, ..., A K, A K+1,..., A K+T , Що містить більш ніж R векторів. Це суперечить доведеному в третій частині.
6 ° Нехай B 1, B 2, ..., B R базис системи S. За визначенням базису будь-який вектор A € S є лінійна комбінація векторів базису:
A \u003d a1 B 1 + a2 B 2 + ... + ar B R.
Доводячи єдиність такого уявлення допустимо противне, що є ще одне подання:
A \u003d b1 B 1 + b2 B 2 + ... + br B R.
Віднімаючи рівності почленно знаходимо
0 \u003d (A1 - b1) B 1 + (a2 - b2) B 2 + ... + (ar - br) B R.
Так як базис B 1, B 2, ..., B R лінійно незалежна система, то всі коефіцієнти ai - bi \u003d 0; I = 1, 2, ..., R. Отже, ai \u003d bi; I = 1, 2, ..., R і єдиність доведена.
Головізін В.В. Лекції з алгебри і геометрії. 5
Лекції з алгебри і геометрії. Семестр 2.
Лекція 23. Базис векторного простору.
Короткий зміст: критерій лінійної залежності системи ненульових векторів, підсистеми системи векторів, що породжує система векторів, мінімальна породжує система і максимальна лінійно незалежна система, базис векторного простору і 4 його рівносильні визначення, розмірність векторного простору, конечномерное векторний простір і існування його базису, доповнення до базису.
п.1. Критерій лінійної залежності системи ненульових векторів.
Теорема. Система ненульових векторів лінійно залежна тоді і тільки тоді, коли знайдеться вектор системи, який лінійно виражається через попередні вектори цієї системи.
Доведення. Нехай система складається з ненульових векторів і лінійно залежна. Розглянемо систему з одного вектора:  . Оскільки
. Оскільки  , То система
, То система  - лінійно незалежна. Приєднаємо до неї вектор
- лінійно незалежна. Приєднаємо до неї вектор  . Якщо отримана система
. Якщо отримана система  лінійно незалежна, то приєднаємо до неї наступний вектор:
лінійно незалежна, то приєднаємо до неї наступний вектор:  . І т.д. продовжуємо до тих пір, поки не отримаємо лінійно залежну систему
. І т.д. продовжуємо до тих пір, поки не отримаємо лінійно залежну систему  , Де. Такий номер обов'язково знайдеться, тому що вихідна система
, Де. Такий номер обов'язково знайдеться, тому що вихідна система  є лінійно залежною за умовою.
є лінійно залежною за умовою.
Отже, з побудови, отримали лінійно залежну систему  , Причому, система
, Причому, система  є лінійно незалежною.
є лінійно незалежною.
система  представляє нульовий вектор нетривіально, тобто знайдеться такої ненульовий набір скалярів
представляє нульовий вектор нетривіально, тобто знайдеться такої ненульовий набір скалярів  , що
, що
де скаляр  .
.
Дійсно, в іншому випадку, якщо  , То ми мали б нетривіальне уявлення нульового вектора лінійно незалежною системою
, То ми мали б нетривіальне уявлення нульового вектора лінійно незалежною системою  , що неможливо.
, що неможливо.
Розділивши останнє рівність на ненульовий скаляр  , Ми можемо висловити з нього вектор
, Ми можемо висловити з нього вектор  :
:
![]() ,
,
Так як зворотне твердження очевидно, то теорема доведена.
п.2. Підсистеми системи векторів векторного простору.
Визначення. Будь-яке непорожнє підмножина системи векторів  називається підсистемою даної системи векторів.
називається підсистемою даної системи векторів.
Приклад. нехай  - система з 10 векторів. Тоді системи векторів:
- система з 10 векторів. Тоді системи векторів:  ;
;
 ,
,
 - підсистеми даної системи векторів.
- підсистеми даної системи векторів.
Теорема. Якщо система векторів містить лінійно залежну підсистему, то сама система векторів теж лінійно залежна.
Доведення. Нехай дана система векторів  і нехай для визначеності підсистема
і нехай для визначеності підсистема  , де
, де  є лінійно залежною. Тоді вона представляє нульовий вектор нетривіально:
є лінійно залежною. Тоді вона представляє нульовий вектор нетривіально:
де серед коефіцієнтів  є хоча б один не рівний нулю. Але тоді рівність є нетривіальне уявлення нульового вектора:
є хоча б один не рівний нулю. Але тоді рівність є нетривіальне уявлення нульового вектора:
звідки, за визначенням, слід лінійна залежність системи  , Ч.т.д.
, Ч.т.д.
Теорема доведена.
Слідство. Будь-яка підсистема лінійно незалежної системи векторів є лінійно незалежною.
Доведення. Припустимо противне. Нехай якась підсистема даної системи є лінійно залежною. Тоді з теореми слід лінійна залежність даної системи, що суперечить умові.
Слідство доведено.
п.3. Системи стовпців арифметичного векторного простору стовпців.
З результатів попереднього параграфа, як окремий випадок, слід теорема.
1) Система стовпців є лінійно залежною тоді і тільки тоді, коли в системі знайдеться хоча б один стовпець, який лінійно виражається через інші стовпці даної системи.
2) Система стовпців є лінійно незалежної тоді і тільки тоді, коли жоден стовпець системи лінійно не виражає через інші стовпці даної системи.
3) Система стовпців, що містить нульовий стовпець є лінійно залежною.
4) Система стовпців, що містить два рівних стовпці є лінійно залежною.
5) Система стовпців, що містить два пропорційних стовпчика є лінійно залежною.
6) Система стовпців, що містить лінійно залежну підсистему, є лінійно залежною.
7) Будь-яка підсистема лінійно незалежної системи стовпців є лінійно незалежною.
Єдине, що, можливо, тут потрібно уточнити це поняття пропорційних стовпців.
Визначення. Два ненульових стовпчика  називають пропорційними, якщо знайдеться скаляр
називають пропорційними, якщо знайдеться скаляр  , Такий, що
, Такий, що  або
або
 ,
,
 ,
…,
,
…,
 .
.
Приклад. система  є лінійно залежною, так як її перші два стовпці пропорційні.
є лінійно залежною, так як її перші два стовпці пропорційні.
Зауваження. Ми вже знаємо (див. Лекцію 21), що визначник дорівнює нулю, якщо система його стовпців (рядків) є лінійно залежною. Надалі буде доведено, що вірно і зворотне твердження: якщо визначник дорівнює нулю, то система його стовпців і система його рядків є лінійно залежними.
п.4. Базис векторного простору.
Визначення. система векторів  векторного простору над полем К називається породжує (утворює) системою векторів цього векторного простору, якщо вона представляє будь-якої його вектор, тобто якщо знайдеться такий набір скалярів
векторного простору над полем К називається породжує (утворює) системою векторів цього векторного простору, якщо вона представляє будь-якої його вектор, тобто якщо знайдеться такий набір скалярів  , Що.
, Що.
Визначення. Система векторів векторного простору називається мінімальної породжує системою, якщо при видаленні з цієї системи будь-якого вектора вона перестає бути породжує системою.
Зауваження. З визначення відразу ж випливає, що якщо породжує система векторів не є мінімальною, то знайдеться хоча б один вектор системи, при видаленні якого з системи, що залишилася система векторів і раніше буде породжує.
Лемма (Про лінійно залежною породжує системі.)
Якщо в лінійно залежною і породжує системі векторів один з векторів лінійно виражається через інші, то його можна видалити з системи і залишилася система векторів буде породжує.
Доведення. нехай система  лінійно залежна і породжує, і нехай один з її векторів лінійно виражається через інші вектори цієї системи.
лінійно залежна і породжує, і нехай один з її векторів лінійно виражається через інші вектори цієї системи.
Для визначеності і для простоти запису допустимо, що
Так як  - породжує система, то
- породжує система, то  знайдеться такий набір скалярів
знайдеться такий набір скалярів  , що
, що
 .
.
Звідси отримуємо,
тобто будь-який вектор х лінійно виражається через вектори системи  , А це означає, що вона є породжує системою, ч.т.д.
, А це означає, що вона є породжує системою, ч.т.д.
Слідство 1. лінійно залежна і породжує система векторів не є мінімальною.
Доведення. Відразу ж випливає з леми і визначення мінімальної породжує системи векторів.
Слідство 2. Мінімальна породжує система векторів є лінійно незалежною.
Доведення. Допустивши противне, приходимо до протиріччя зі слідством 1.
Визначення. Система векторів векторного простору називається максимальною лінійно незалежною системою, якщо при додаванні до цієї системи будь-якого вектора вона стає лінійно залежною.
Зауваження. З визначення відразу ж випливає, що якщо система є лінійно незалежної, але не максимальної, то знайдеться вектор, при додаванні якого до системи, виходить лінійно незалежна система.
Визначення. Базисом векторного простору V над полем K називається впорядкована система його векторів, що представляє будь-який вектор векторного простору єдиним способом.
Інакше кажучи, система векторів  векторного простору V над полем K називається його базисом, якщо
векторного простору V над полем K називається його базисом, якщо  існує єдиний набір скалярів
існує єдиний набір скалярів  , Такий, що.
, Такий, що.
Теорема. (Про чотирьох рівносильних визначеннях базису.)
нехай  - упорядкована система векторів векторного простору. Тоді наступні твердження рівносильні:
- упорядкована система векторів векторного простору. Тоді наступні твердження рівносильні:
1. Система  є базисом.
є базисом.
2. Система  є лінійно незалежної і породжує системою векторів.
є лінійно незалежної і породжує системою векторів.
3. Система  є максимальною лінійно незалежною системою векторів.
є максимальною лінійно незалежною системою векторів.
4. Система  є мінімальною породжує системою векторів.
є мінімальною породжує системою векторів.
Доведення.
Нехай система векторів  є базисом. З визначення базису відразу ж випливає, що ця система векторів є породжує системою векторів векторного простору, тому нам потрібно тільки довести її лінійну незалежність.
є базисом. З визначення базису відразу ж випливає, що ця система векторів є породжує системою векторів векторного простору, тому нам потрібно тільки довести її лінійну незалежність.
Припустимо, що дана система векторів лінійно залежна. Тоді існує два подання нульового вектора - тривіальне і нетривіальне, що суперечить визначенню базису.
Нехай система векторів  є лінійно незалежної і породжує. Нам потрібно довести, що дана лінійно незалежна система є максимальною.
є лінійно незалежної і породжує. Нам потрібно довести, що дана лінійно незалежна система є максимальною.
Припустимо противне. Нехай дана лінійно незалежна система векторів не є максимальною. Тоді, в силу зауваження вище, знайдеться вектор, який можна буде додати до цієї системи і отримана система векторів залишається лінійно незалежною. Однак, з іншого боку, доданий до системи вектор може бути представлений у вигляді лінійної комбінації вихідної системи векторів в силу того, що вона є породжує системою.
І ми отримуємо, що в новій, розширеній, системі векторів один з її векторів лінійно виражається через інші вектори цієї системи. Така система векторів є лінійно залежною. Отримали протиріччя.
Нехай система векторів  векторного простору є максимальною лінійно незалежною. Доведемо, що вона є мінімальною породжує системою.
векторного простору є максимальною лінійно незалежною. Доведемо, що вона є мінімальною породжує системою.
а) Спочатку доведемо, що вона є породжує системою.
Зауважимо, що в силу лінійної незалежності, система  не містить нульового вектора. Нехай - довільний ненульовий вектор. Додамо його до даної системи векторів:
не містить нульового вектора. Нехай - довільний ненульовий вектор. Додамо його до даної системи векторів:  . Отримана система ненульових векторів є лінійно залежною, тому що вихідна система векторів максимальна лінійно незалежна. Значить, в цій системі, знайдеться вектор лінійно виражається через попередні. У вихідній лінійно незалежної системи
. Отримана система ненульових векторів є лінійно залежною, тому що вихідна система векторів максимальна лінійно незалежна. Значить, в цій системі, знайдеться вектор лінійно виражається через попередні. У вихідній лінійно незалежної системи  жоден з векторів не може виражатися через попередні, отже, лінійно виражається через попередні тільки вектор х. Таким чином, система
жоден з векторів не може виражатися через попередні, отже, лінійно виражається через попередні тільки вектор х. Таким чином, система  представляє будь-який ненульовий вектор. Залишилося помітити, що дана система, очевидно, представляє і нульовий вектор, тобто система
представляє будь-який ненульовий вектор. Залишилося помітити, що дана система, очевидно, представляє і нульовий вектор, тобто система  є породжує.
є породжує.
б) Тепер доведемо її мінімальність. Припустимо противне. Тоді один з векторів системи може бути видалений з системи і залишилася система векторів і раніше буде породжує системою і, отже, віддалений з системи вектор теж лінійно виражається через що залишилися вектора системи, що суперечить лінійної незалежності вихідної системи векторів.
Нехай система векторів  векторного простору є мінімальною породжує системою. Тоді вона представляє будь-який вектор векторного простору. Нам потрібно довести єдиність подання.
векторного простору є мінімальною породжує системою. Тоді вона представляє будь-який вектор векторного простору. Нам потрібно довести єдиність подання.
Припустимо противне. Нехай який-небудь вектор х лінійно виражається через вектори даної системи двома різними способами:
Віднімаючи з одного рівності інше, одержуємо:
В силу слідства 2, система  є лінійно незалежної, тобто представляє нульовий вектор тільки трівмально, тому всі коефіцієнти цієї лінійної комбінації повинні бути рівні нулю:
є лінійно незалежної, тобто представляє нульовий вектор тільки трівмально, тому всі коефіцієнти цієї лінійної комбінації повинні бути рівні нулю:
Таким чином, будь-який вектор х лінійно виражається через вектори даної системи єдиним способом, ч.т.д.
Теорема доведена.
п.5. Розмірність векторного простору.
Теорема 1. (Про число векторів в лінійно незалежних і породжують системах векторів.) Число векторів в будь-який лінійно незалежної системи векторів не перевищує числа векторів в будь-який породжує системі векторів цього ж векторного простору.
Доведення. нехай  довільна лінійно незалежна система векторів,
довільна лінійно незалежна система векторів,  - довільна породжує система. Припустимо, що.
- довільна породжує система. Припустимо, що.
Оскільки  породжує система, то вона являє будь-який вектор простору, в тому числі і вектор
породжує система, то вона являє будь-який вектор простору, в тому числі і вектор  . Приєднаємо його до цієї системи. Отримуємо лінійно залежну і породжує систему векторів:
. Приєднаємо його до цієї системи. Отримуємо лінійно залежну і породжує систему векторів:  . Тоді знайдеться вектор
. Тоді знайдеться вектор  цієї системи, який лінійно виражається через попередні вектори цієї системи і його, в силу леми, можна видалити з системи, причому залишилася система векторів буде як і раніше породжує.
цієї системи, який лінійно виражається через попередні вектори цієї системи і його, в силу леми, можна видалити з системи, причому залишилася система векторів буде як і раніше породжує.
 . Оскільки ця система породжує, то вона являє вектор
. Оскільки ця система породжує, то вона являє вектор  і, приєднуючи його до цієї системи, знову отримуємо лінійно залежну і породжує систему:.
і, приєднуючи його до цієї системи, знову отримуємо лінійно залежну і породжує систему:.
Далі все повторюється. Знайдеться вектор в цій системі, який лінійно виражається через попередні, причому це не може бути вектор  , Тому що вихідна система
, Тому що вихідна система  лінійно незалежна і вектор
лінійно незалежна і вектор  не виражає лінійно через вектор
не виражає лінійно через вектор  . Значить, це може бути тільки один з векторів
. Значить, це може бути тільки один з векторів  . Видаляючи його із системи, отримуємо, після перенумерованія, систему, яка буде породжує системою. Продовжуючи цей процес, через кроків отримаємо породжує систему векторів:, де
. Видаляючи його із системи, отримуємо, після перенумерованія, систему, яка буде породжує системою. Продовжуючи цей процес, через кроків отримаємо породжує систему векторів:, де  , Тому що за нашим припущенням. Значить, ця система, як породжує, представляє і вектор, що суперечить умові лінійної незалежності системи
, Тому що за нашим припущенням. Значить, ця система, як породжує, представляє і вектор, що суперечить умові лінійної незалежності системи  .
.
Теорема 1 доведена.
Теорема 2. (Про кількість векторів у базисі.) У будь-якому базисі векторного простору міститься одне і теж число векторів.
Доведення. нехай  і
і  - два довільних базису векторного простору. Будь-базис є лінійно незалежної і породжує системою векторів.
- два довільних базису векторного простору. Будь-базис є лінійно незалежної і породжує системою векторів.
Оскільки перша система лінійно незалежна, а друга - породжує, то, по теоремі 1,  .
.
Аналогічно, друга система лінійно незалежна, а перша - породжує, то. Звідси слідує що  , Ч.т.д.
, Ч.т.д.
Теорема 2 доведена.
Дана теорема дозволяє ввести таке визначення.
Визначення. Розмірністю векторного простору V над полем K називається число векторів в його базисі.
позначення:  або
або  .
.
п.6. Існування базису векторного простору.
Визначення. Векторний простір називається конечномірні, якщо воно володіє кінцевою породжує системою векторів.
Зауваження. Ми будемо вивчати тільки скінченномірні векторні простору. Незважаючи на те, що ми вже досить багато знаємо про базис конечномерного векторного простору, у нас немає впевненості, що базис такого простору взагалі існує. Всі раніше отримані властивості були отримані в припущенні, що базис існує. Наступна теорема закриває це питання.
Теорема. (Про існування базису конечномерного векторного простору.) Будь-яке конечномерное векторний простір має базисом.
Доведення. За умовою існує кінцева породжує система векторів даного конечномерного векторного простору V:  .
.
Зауважимо відразу ж, що якщо породжує система векторів є марною, тобто не містить жодного вектора, то за визначенням вважають, що дане векторне простір є нульовим, тобто  . У цьому випадку за визначенням вважають, що базисом нульового векторного простору є порожній базис і його розмірність за визначенням вважають рівною нулю.
. У цьому випадку за визначенням вважають, що базисом нульового векторного простору є порожній базис і його розмірність за визначенням вважають рівною нулю.
Нехай далі, нульове векторний простір і  кінцева породжує система ненульових векторів. Якщо вона лінійно незалежна, то все доведено, тому що лінійно незалежна і породжує система векторів векторного простору є його базисом. Якщо ж дана система векторів є лінійно залежною, то один з векторів цієї системи лінійно виражається через що залишилися і його можна видалити з системи, причому залишилася система векторів, в силу леми п.5, буде як і раніше породжує.
кінцева породжує система ненульових векторів. Якщо вона лінійно незалежна, то все доведено, тому що лінійно незалежна і породжує система векторів векторного простору є його базисом. Якщо ж дана система векторів є лінійно залежною, то один з векторів цієї системи лінійно виражається через що залишилися і його можна видалити з системи, причому залишилася система векторів, в силу леми п.5, буде як і раніше породжує.
Перенумеруем залишилася систему векторів:  . Далі міркування повторюються. Якщо ця система лінійно незалежна, то вона є базисом. Якщо ж ні, то знову знайдеться вектор в цій системі, який можна видалити, а що залишилася система буде породжує.
. Далі міркування повторюються. Якщо ця система лінійно незалежна, то вона є базисом. Якщо ж ні, то знову знайдеться вектор в цій системі, який можна видалити, а що залишилася система буде породжує.
Повторюючи цей процес, ми не можемо залишитися з порожньою системою векторів, тому що в самому крайньому випадку ми прийдемо до породжує системі з одного ненульового вектора, яка є лінійно незалежної, а, отже, базисом. Тому, на якомусь етапі ми приходимо до лінійно незалежної і породжує системі векторів, тобто до базису.
Теорема доведена.
Лемма. Нехай. тоді:
1. Будь-яка система з вектора є лінійно залежною.
2. Будь-яка лінійно незалежна система з векторів є його базисом.
Доведення. 1). За умовою леми, число векторів в базисі одно і базис є породжує системою, тому число векторів в будь-який лінійно незалежної системи не може перевершувати.
2). Як випливає з тільки що доведеного, будь-яка лінійно незалежна система з векторів цього векторного простору є максимальною, а отже, базисом.
Лема доведена.
Теорема (Про доповнення до базису.) Будь-яка лінійно незалежна система векторів векторного простору може бути доповнена до базису цього простору.
Доведення. Нехай векторне простір розмірності n і  деяка лінійно незалежна система його векторів. тоді
деяка лінійно незалежна система його векторів. тоді  .
.
якщо  , То за попередньою лемі, ця система є базисом і доводити нічого.
, То за попередньою лемі, ця система є базисом і доводити нічого.
Якщо ж  , Тоді дана система є не максимальної лінійної незалежною системою (інакше вона була б базисом, що неможливо, тому що). Отже, знайдеться вектор
, Тоді дана система є не максимальної лінійної незалежною системою (інакше вона була б базисом, що неможливо, тому що). Отже, знайдеться вектор  , Такий, що система
, Такий, що система  - лінійно незалежна.
- лінійно незалежна.
Якщо, тепер, то система  є базисом.
є базисом.
Якщо ж  , Все повторюється. Процес поповнення системи не може тривати нескінченно, тому що на кожному кроці ми отримуємо лінійно незалежну систему векторів простору, а за попередньою лемі число векторів в такій системі не може перевищувати розмірності простору. Отже, на якомусь етапі ми прийдемо до базису даного простору.
, Все повторюється. Процес поповнення системи не може тривати нескінченно, тому що на кожному кроці ми отримуємо лінійно незалежну систему векторів простору, а за попередньою лемі число векторів в такій системі не може перевищувати розмірності простору. Отже, на якомусь етапі ми прийдемо до базису даного простору.
Теорема доведена.
п.7. Приклад.
1. Нехай К - довільне поле, - арифметичне векторний простір стовпців висоти. Тоді. Для доказу розглянемо систему стовпців цього простору.
Називається конечномірні, якщо воно володіє кінцевою породжує системою векторів.
Зауваження. Ми будемо вивчати тільки скінченномірні векторні простору. Незважаючи на те, що ми вже досить багато знаємо про базис конечномерного векторного простору, у нас немає впевненості, що такого простору взагалі існує. Всі раніше отримані були отримані в припущенні, що базис існує. Наступна закриває це питання.
Теорема. (Про існування базису конечномерного векторного простору.)
Будь-яке конечномерное векторний простір має базисом.
Доведення. За умовою існує кінцева породжує система даного конечномерного векторного простору V:.
Зауважимо відразу ж, що якщо породжує система векторів є марною, тобто не містить жодного вектора, то за визначенням вважають, що дане векторне простір є нульовим, тобто . У цьому випадку за визначенням вважають, що базисом нульового векторного простору є порожній базис і його по визначенню вважають рівною нулю.
Якщо ця система незалежна, то все доведено, тому що лінійно незалежна і породжує система векторів векторного простору є його базисом.
Якщо ж дана система векторів є лінійно залежною, то один з векторів цієї системи лінійно виражається через що залишилися і його можна видалити з системи, причому залишилася система векторів, буде як і раніше породжує.
Перенумеруем залишилася систему векторів:. Далі міркування повторюються.
Якщо ця система лінійно незалежна, то вона є базисом. Якщо ж ні, то знову знайдеться вектор в цій системі, який можна видалити, а що залишилася система буде породжує.
Повторюючи цей процес, ми не можемо залишитися з порожньою системою векторів, тому що в самому крайньому випадку ми прийдемо до породжує системі з одного ненульового вектора, яка є лінійно незалежної, а, отже, базисом. Тому, на якомусь етапі ми приходимо до лінійно незалежної і породжує системі векторів, тобто до базису, ч.т.д.
Теорема доведена.
Лемма. (Про системи векторів в n-вимірному векторному просторі.)
Нехай. тоді:
1. Будь-яка система з вектора є лінійно залежною.
2. Будь-яка лінійно незалежна система з векторів є його базисом.
Доведення. 1). За умовою леми, число векторів в базисі одно і базис є породжує системою, тому число векторів в будь-який лінійно незалежної системи не може перевершувати, тобто будь-яка система містить вектор є лінійно залежною.
2). Як випливає з тільки що доведеного, будь-яка лінійно незалежна система з векторів цього векторного простору є максимальною, а отже, базисом.
Лема доведена.
Теорема (Про доповнення до базису.) Будь-яка лінійно незалежна система векторів векторного простору може бути доповнена до базису цього простору.
Доведення. Нехай векторне простір розмірності n і деяка лінійно незалежна система його векторів. Тоді.
Якщо, то за попередньою лемі, ця система є базисом і доводити нічого.
Якщо ж, тоді дана система є не максимальної незалежної системою (інакше вона була б базисом, що неможливо, тому що). Отже, знайдеться вектор, такий, що система ![]() - лінійно незалежна.
- лінійно незалежна.
Якщо, тепер, то система ![]() є базисом.
є базисом.
Якщо ж, все повторюється. Процес поповнення системи не може тривати нескінченно, тому що на кожному кроці ми отримуємо лінійно незалежну систему векторів простору, а за попередньою лемі число векторів в такій системі не може перевищувати розмірності простору. Отже, на якомусь етапі ми прийдемо до базису даного простору., Ч.т.д.
Визначення. базис
арифметичного векторного простору стовпців висоти n називається канонічним або природним.
 Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок
Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок Ефективний пошук роботи Курс з пошуку роботи
Ефективний пошук роботи Курс з пошуку роботи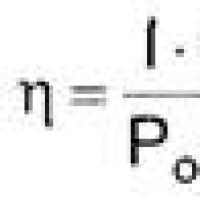 Основні характеристики і параметри фотодіода
Основні характеристики і параметри фотодіода Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF
Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF Чому згорнуте вікно програми довго розгортається?
Чому згорнуте вікно програми довго розгортається? DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt
DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt Що робити якщо пропав курсор миші
Що робити якщо пропав курсор миші