Kötet - Térmodell. A modellezés típusainak osztályozása. Dinamikus modellek. Példák dinamikus modellek felépítésére Térbeli és dinamikus modellek
A műszaki objektumok egyes elemeinek térbeli integrációja széles körben elterjedt tervezési probléma a technológia bármely ágában: rádióelektronikában, gépészetben, energetikában stb. A térmodellezés jelentős részét az egyes elemek és egy műszaki objektum mint pl. a probléma megoldására szolgáló grafikus alkalmazások algoritmusai és szoftveres megvalósítása.
Az elemmodellek felépítése univerzális jellegű, és számos térmodellezési és műszaki objektumok számítógépes tervezési rendszerének változatlan részének tekinthető.
Az alkalmazott grafikus környezet képességeitől függetlenül a grafikus modellek kialakításának jellege szerint az elemek három csoportja különíthető el:
1.Egyedi elemek, amelyek konfigurációja és méretei más hasonló részeken nem ismétlődnek.
2. Egységes elemek, beleértve az alkatrészekre jellemző konfigurációtöredékeket ebből az osztályból... Általános szabály, hogy egy egységes elemnek korlátozott számú szabványos mérete létezik.
3. Összetett elemek, amelyek egy tetszőleges halmazban egyedi és egységes elemeket is tartalmaznak. A használt grafika lehetővé teheti az összetett elemek beágyazását.
Az egyedi elemek térbeli modellezése nem túl nehéz. A modellkonfiguráció közvetlen kialakítása interaktív módban történik, majd a szoftveres implementáció a modellalkotási protokoll vagy a kapott elem szöveges leírása alapján történik.
2. A térbeli konfigurációjú töredékek szekvenciális kiválasztása és méretük meghatározása;
3. Egy elem grafikus modelljének kötése más elemekhez, műszaki objektumokhoz vagy rendszerekhez;
4. További információk megadása a modellezett elemről
Az egyesített elemek modelljeinek kialakításának ez a megközelítése megbízható szoftvermegvalósítást biztosít.
Az alkotómodell egyedi és egységes modellelemek gyűjteményéből áll. Az összetett elem modellje eljárásilag az egységes elem modelljéhez hasonlóan épül fel, amelyben az elemek kész modelljei grafikus töredékként működnek. A fő jellemzők a mellékelt modellek összekapcsolásának módja és az egyes töredékek kompozit elemmé kombinálásának mechanikája. Ez utóbbit elsősorban a grafikus eszközök képességei határozzák meg.
A grafikus környezet és a műszaki információkat tartalmazó adatbázis-kezelő rendszer (DBMS) integrációja biztosítja a modellezési rendszer nyitottságát egyéb tervezési problémák megoldására is: előzetes tervezési számítások, elembázis kiválasztása, tervdokumentáció (szöveges és grafikus) stb. Az adatbázisok (DB) a grafikus modellek követelményei és a kapcsolódó feladatok információigényei. Eszközként bármilyen grafikus környezettel összekapcsolt DBMS használható. A legáltalánosabb természet az egységes elemekből álló modellek felépítése. Az első szakaszban az azonos típusú elemek nómenklatúrájának rendszerezése eredményeként a cél és a grafikai töredékek összetétele egy hipotetikus minta jön létre, vagy egy modellezett elem meglévő mintáját választják ki, amely teljes modellezett készlettel rendelkezik. a tárgy részei.
Interpolációs módszerek diszkrét pontokhoz.
A pontok szerinti interpoláció általános problémája a következőképpen fogalmazódik meg: számos pont (interpolációs csomópont) van megadva, amelyekben ismert a jellemzők helyzete és értékei, meg kell határozni a jellemzők értékeit egyéb pontok, amelyeknek csak a pozíciója ismert. Ugyanakkor megkülönböztetik a globális és lokális interpoláció módszereit, amelyek között vannak egzakt és közelítő módszerek.
A teljes területre kiterjedő globális interpoláció esetén egyetlen számítási funkciót használunk egyszerre z = F (x, y). Ebben az esetben egy érték módosítása (x, y) a bemeneten a teljes eredő DEM-et érinti. Lokális interpoláció esetén a számítási algoritmust ismételten alkalmazzák néhány mintára egy közös ponthalmazból, rendszerint egymáshoz közel. Ezután a pontok kiválasztásának változása csak a terület egy kis területének feldolgozásának eredményeit érinti. A globális interpolációs algoritmusok sima felületeket hoznak létre, kevés hirtelen változással; olyan esetekben használatosak, amikor a felület alakját ismertnek tételezzük fel, például trend esetén. Ha a teljes adatkészlet nagy része bekerül a helyi interpolációs folyamatba, az lényegében globálissá válik.
Precíz interpolációs technikák.
Pontos interpolációs módszerek reprodukálja az adatokat azokban a pontokban (csomópontokban), amelyeken az interpoláció alapul, és a felület áthalad az összes ismert értékű ponton. szomszédsági elemzés, amelyben a szimulált jellemzők összes értékét egyenlőnek tekintjük a legközelebbi ismert pont értékeivel. Ennek eredményeként a Thyssen-sokszögek a határokon éles értékváltozással jönnek létre. Ezt a módszert a környezeti vizsgálatokban, hatászónák értékelésénél alkalmazzák, és inkább névleges adatokra alkalmas.
A módszerben B-spline darabonkénti lineáris polinom létrehozása, amely lehetővé teszi olyan szakaszok sorozatának létrehozását, amelyek végül egy felületet alkotnak folytonos első és második deriválttal. A módszer biztosítja a magasságok, lejtések, görbületek folytonosságát. Az így kapott DEM raszteres formában van. Ezt a helyi interpolációs módszert főleg sima felületekre használják, és nem alkalmas olyan felületekre, ahol kifejezett változások vannak - ez éles ingadozásokhoz vezet a spline-ban. Széles körben használják az általános célú felületinterpolációs és kontúrsimító programokban ezek rajzolásakor.
Az TIN modellekben az egyes háromszögeken belüli felületet általában egy sík ábrázolja. Mivel minden háromszög három csúcsának magasságával van beállítva, egy közös mozaikfelületen a szomszédos szakaszokhoz tartozó háromszögek pontosan illeszkednek az oldalakhoz: a kialakult felület folytonos. Ha azonban vízszinteseket rajzolunk a felületre, akkor ebben az esetben egyenesek és párhuzamosak lesznek a háromszögeken belül, és a határokon éles irányváltozás következik be. Ezért egyes TIN-alkalmazások esetében minden háromszögön belül egy matematikai felületet hoznak létre, amelyet a háromszögek határain a lejtőszögek egyenletes változása jellemez. Trendek elemzése. A felületet polinom közelíti, a kimenet pedig algebrai függvényként strukturált, amellyel értékeket számíthat ki a raszteres pontokon vagy a felületen bárhol. Lineáris egyenlet, mint pl z = a + bx + su ferde sík felületet ír le, és a másodfokú z = egy + bx + su + dx2 + exu + fy2 -egyszerű domb vagy völgy. Általánosságban elmondható, hogy a felület bármely szakasza th a rendnek nincs több (T - 1) váltakozó csúcsok és mélypontok. Például egy köbfelületnek bármely szakaszában lehet egy maximum és egy minimum. Jelentős élhatások lehetségesek, mivel a polinommodell konvex felületet hoz létre.
Mozgóátlag és távolság súlyozott átlag módszerei legszélesebb körben használják, különösen simán változó felületek modellezésére. Az interpolált értékek az értékek átlagát jelentik P ismert pontokat, vagy az interpolált pontokból kapott átlagot, és általában a képlettel ábrázoljuk
Közelítő módszerek az interpolációhoz.
Közelítő interpolációs módszerek olyan esetekben használják, amikor bizonyos bizonytalanság van a rendelkezésre álló felületi adatokkal kapcsolatban; azon alapulnak, hogy sok adathalmaz lassan változó felületi trendet mutat, amely a helyi, gyorsan változó eltérésekre rakódik rá, ami pontatlanságokhoz vagy hibákhoz vezet az adatokban. Ilyen esetekben a felület közelítéssel történő simítás csökkentheti a hibás adatok hatását a kapott felület karakterére.
Interpolációs módszerek a területekhez.
A terület szerinti interpoláció az adatok átvitele az egyik forrásterület-készletből (kulcs) egy másik halmazba (cél), és gyakran használják egy terület zónázásakor. Ha a célterületek kulcsterületek csoportosítása, ez egyszerű. Nehézségek merülnek fel, ha a célterületek határai nem kapcsolódnak az eredeti kulcsterületekhez.
Tekintsünk két lehetőséget a terület szerinti interpolációra: az elsőben az interpoláció eredményeként a célterületek interpolált mutatójának összértéke (például népességszám) nem marad meg maradéktalanul, a másodikban pedig megmarad.
Képzelje el, hogy vannak népességi adatok bizonyos területekre adott határokkal, és ezeket ki kell terjeszteni egy finomabb zónahálóra, amelynek határai általában nem esnek egybe az elsővel.
A technika a következő. Minden egyes forrásterületre (kulcsterületre) a népsűrűséget úgy számítják ki, hogy a teljes lakosok számát elosztják a helyszín területével, és az így kapott értéket a központi ponthoz (centroid) rendelik. Ezen pontkészlet alapján, a fent leírt módszerek egyikével, egy szabályos rácsot interpolálnak, a hálózat minden cellájánál a populációt úgy határozzák meg, hogy megszorozzák a számított sűrűséget a cella területével. Az interpolált rács rákerül a kapott térképre, az egyes cellák értékei a megfelelő célterület határaira vonatkoznak. Ezután kiszámítjuk az egyes így kapott körzetek összlakosságát.
A módszer hátrányai közé tartozik a központi pont kiválasztásának nem teljesen egyértelmű meghatározása; A pontonkénti interpolációs módszerek nem megfelelőek, és ami a legfontosabb, a kulcsterületek interpolált mutatójának összértéke (jelen esetben a népszámlálási területek összlakossága) nem kerül mentésre. Például, ha a forrászóna két célzónára van felosztva, akkor az ezekben lévő teljes populáció az interpoláció után nem feltétlenül lesz egyenlő a forrászóna populációjával.
Az interpoláció második változatában a térinformatikai technológiás átfedés, vagy sima felület kialakításának módszereit alkalmazzák, amelyek az úgynevezett adaptív interpoláción alapulnak.
Az első módszerben a kulcs- és célterületeket egymásra helyezzük, meghatározzuk az egyes kezdeti területek részesedését a célterületeken, az egyes kezdeti területek mutatóinak értékeit felosztjuk a különböző parcellák területeinek arányában. célterületek. Úgy tekintjük, hogy a mutató sűrűsége az egyes területeken belül azonos, például ha a mutató a terület összlakossága, akkor a népsűrűséget állandónak tekintjük.
A második módszer célja, hogy sima felületet hozzon létre párkányok nélkül (az attribútumértékek nem változhatnak hirtelen a területek határain), és az indikátor összértékének fenntartása az egyes területeken belül. Technikája a következő. A kulcsterületeket ábrázoló kartogramra egy sűrű raszter kerül ráhelyezve, az egyes területek indikátorának összértéke egyenlően oszlik el a raszter átfedő cellái között, az értékek simításra kerülnek úgy, hogy a raszter minden cellájának értékét helyettesítjük a környék átlaga (2 × 2, 3 × 3, 5 × 5 ablaknál), és összegezze az egyes területek összes cellájának értékét. Továbbá az összes cella értékeit arányosan állítják be úgy, hogy a terület indikátorának összértéke egybeessen az eredeti értékkel (például ha az összeg 10%-kal kisebb, mint az eredeti érték, akkor az egyes cellák értékei sejt 10%-kal nő. Az eljárást addig ismételjük. a változások leállnak.
Az ismertetett módszernél a tartományokon belüli homogenitás nem szükséges, de a határokon belüli túl erős eltérések az indikátorban befolyásolhatják az interpoláció minőségét.
Az eredmények a térképen kontúrvonalakkal vagy folyamatos féltónusokkal ábrázolhatók.
A módszer alkalmazása megköveteli bizonyos peremfeltételek felállítását, hiszen az eredeti területek perifériája mentén a raszterelemek túlléphetnek a vizsgált területen, vagy olyan területekkel szomszédosak, amelyek nem rendelkeznek az interpolált indikátor értékével. Hozzárendelheti például a népsűrűséget 0-hoz (tó stb.), vagy egyenlőnek veheti a vizsgált terület középpontjától legtávolabbi cellák értékével.
Területenkénti interpoláció esetén nagyon nehéz esetek adódhatnak, például amikor az egyes városok népességére vonatkozó adatok alapján térképet kell készíteni, amelyen az "elterjedési területek" láthatók, különösen, ha ezeket a területeket a térkép léptékén egy pont. A probléma kis forrásterületeknél is jelentkezik, amikor nincsenek határfájlok, és csak a középpont pozíciója van feltüntetve az adatokban. Itt különböző megközelítések lehetségesek: a pontokat, amelyekhez az adatok hozzá vannak rendelve, körökkel helyettesítjük, amelyek sugarát a szomszédos centroidok távolságai alapján becsüljük meg; a népsűrűség küszöbértékének meghatározása egy terület városi területhez való hozzárendeléséhez; az egyes városok lakosságának eloszlása a területükön úgy, hogy a központban nagyobb legyen a népsűrűség, a külterületeken pedig csökken; a mutató küszöbértékével ellátott pontok mentén vonalak húzódnak, amelyek korlátozzák a lakott területeket.
Gyakran előfordul, hogy a csak pontszerű adatokból területinterpolációval folyamatos felület létrehozása helytelen eredményekhez vezet.
A felhasználó általában szubjektíven és elsősorban vizuálisan értékeli a módszer alkalmazásának sikerességét. Mostanáig sok kutató alkalmaz kézi interpolációt vagy „szemmel” interpolációt (ezt a módszert általában nem értékelik nagyra a geográfusok és térképészek, de a geológusok széles körben alkalmazzák). Jelenleg a szakértők tudásának a tudásbázisok létrehozásának módszereivel történő „kinyerésére” és egy interpolációt végző szakértői rendszerbe történő bevezetésére tesznek kísérletet.
A modellt statikusnak nevezzük, ha a bemeneti és kimeneti műveletek időben állandóak. Statikus modell az egyensúlyi állapotot írja le.
Egy modellt dinamikusnak nevezünk, ha a bemeneti és kimeneti változók idővel változnak. Dinamikus modell leírja a vizsgált objektum tranziens üzemmódját.
Az objektumok dinamikus tulajdonságainak tanulmányozása lehetővé teszi, hogy a Huygens-Hadamard-féle bizonyosság alapelvének megfelelően választ adjunk arra a kérdésre: hogyan változik egy objektum állapota ismert hatások hatására és adott kezdeti állapot esetén.
A statikus modellre példa a technológiai művelet időtartamának az erőforrások költségétől való függése. A statikus modellt az algebrai egyenlet írja le
A dinamikus modellre példa a vállalkozás kereskedelmi kibocsátásának volumenének függősége a tőkebefektetések méretétől és időzítésétől, valamint a ráfordított erőforrásoktól.
A dinamikus modellt gyakran differenciálegyenlettel írják le
Az egyenlet köti az ismeretlen változót Yés származékai független változóval tés egy adott időfüggvény X (t)és származékai.
Egy dinamikus rendszer működhet folyamatos vagy diszkrét időben, egyenlő időközönként kvantálva. Az első esetben a rendszert egy differenciálegyenlet, a második esetben pedig egy véges differenciálegyenlet írja le.
Ha a bemeneti, kimeneti változók és idők halmazai végesek, akkor a rendszert a állapotgép.
Egy állapotgépet a bemeneti állapotok véges halmaza jellemez; állapotok véges halmaza; belső állapotok véges halmaza; átmeneti funkció T (x, q) a belső állapotok változásának sorrendjének meghatározása; kimenetek funkciója P (x, q) a kimenet állapotának beállítása a bemenet állapotától és a belső állapottól függően.
A determinisztikus automaták általánosítása sztochasztikus automaták, amelyeket az egyik állapotból a másikba való átmenet valószínűségével jellemeznek. Ha egy dinamikus rendszer működése a felmerülő igények kiszolgálása, akkor a rendszermodell a metódusok segítségével készül sorban állás elmélet.
A dinamikus modellt ún helyhez kötött ha a bemeneti változók transzformációs tulajdonságai idővel nem változnak. Különben úgy hívják nem helyhez kötött.
Megkülönböztetni determinisztikus és sztochasztikus (valószínűségi) modell. A determinisztikus operátor lehetővé teszi, hogy az ismert bemeneti változókból egyértelműen meghatározzuk a kimeneti változókat.
Determinizmus modellek csak azt jelentik a bemeneti változók transzformációjának nem véletlenszerűsége, amelyek maguk is lehetnek determinisztikusak és véletlenszerűek is.
A sztochasztikus operátor lehetővé teszi a bemeneti változók valószínűségi eloszlásának meghatározását a bemeneti változók és rendszerparaméterek adott valószínűségi eloszlásából.
A bemeneti és kimeneti változók tekintetében a modelleket a következőképpen osztályozzuk:
1. A bemeneti változók fel vannak osztva sikerültés ellenőrizhetetlen... Az előbbieket a kutató belátása szerint módosíthatja, és a tárgy felhasználja. Utóbbiak vezetésre alkalmatlanok.
2. A bemeneti és kimeneti változók vektorainak méretétől függően megkülönböztetünk egydimenziós és többdimenziós modellek. Az egydimenziós modell alatt olyan modellt értünk, amelyben a bemeneti és kimeneti változók egyidejűleg skaláris mennyiségek. A többdimenziós modell olyan modell, amelyben a vektorok x(t) és y(t) mérettel rendelkezik n³ 2.
3. Olyan modelleket nevezünk, amelyekben a bemeneti és kimeneti változók időben és nagyságrendben folytonosak folyamatos... Olyan modelleket hívunk, amelyekben a bemeneti és kimeneti változók időben vagy nagyságrendben diszkrétek diszkrét.
Vegye figyelembe, hogy a komplex rendszerek dinamikája nagymértékben függ az emberek döntéseitől. Az összetett rendszerekben lezajló folyamatokat nagyszámú paraméter jellemzi – nagy abból a szempontból, hogy a megfelelő egyenletek és összefüggések nem oldhatók meg analitikusan. A gyakran vizsgált komplex rendszerek egyedülállóak a hasonló célú rendszerekhez képest is. Az ilyen rendszerekkel végzett kísérletek időtartama általában hosszú, és gyakran összemérhető az élettartamukkal. Néha a rendszerrel végzett aktív kísérletek általában elfogadhatatlanok.
Egy összetett objektum esetében gyakran lehetetlennek bizonyul az egyes vezérlési lépések tartalmának meghatározása. Ez a körülmény olyan nagyszámú helyzetet határoz meg, amely az objektum állapotát jellemzi, hogy gyakorlatilag lehetetlen elemezni mindegyiknek a meghozott döntésekre gyakorolt hatását. Ebben a helyzetben ahelyett, hogy egy merev vezérlőalgoritmus a megvalósítás minden lépésében egy bizonyos egyértelmű megoldást írna elő, egy olyan utasításkészletet kell használni, amely megfelel a matematikában általában számításnak. A számítási algoritmussal ellentétben a folyamat folytatása az egyes lépésekben nem rögzített, és lehetőség van a megoldáskeresési folyamat tetszőleges folytatására. A számításokat és hasonló rendszereket a matematikai logika tanulmányozza.
1.5. Az összetett objektumok rendszermodelljének felépítésének koncepciója
Az összetett objektumok különálló, szerkezetileg elszigetelt elemek összessége: technológiai egységek, közlekedési utak, elektromos hajtások stb., amelyeket anyag, energia és információáramlások, és interakcióba lép vele környezet mint egész. Az összetett objektumokban lezajló energia- és tömegcsere folyamatok irányítottak és a mezők és az anyag mozgásával (hőcsere, szűrés, diffúzió, deformáció stb.) kapcsolódnak. Ezek a folyamatok általában instabil fejlődési szakaszokat tartalmaznak, és az ilyen folyamatok kezelése inkább művészet, mint tudomány. E körülmények miatt az ilyen objektumok kezelésének minősége instabil. A technológiai személyzet képesítésével szemben támasztott követelmények meredeken emelkednek, és a képzésük ideje jelentősen megnő.
A rendszer eleme egy bizonyos objektum (anyag, energia, információ), amely számos számunkra fontos tulajdonsággal rendelkezik, amelynek belső szerkezete (tartalma) az elemzés célja szempontjából nem érdekes.
Az elemeket jellel fogjuk jelölni M, és azok teljes mérlegelt (lehetséges) halmaza - keresztül (M)... Egy elem halmazhoz való tartozását szokás rögzíteni.
Kommunikáció Nevezzük meg az elemek közötti cserét, ami a mérlegelés szempontjából fontos: anyag, energia, információ.
Egyetlen kommunikációs aktus az hatás... Egy elem összes hatásának kijelölése M Tételenként 1 db M 2 keresztül x 12, és az elem M 2 on M 1 - keresztül x A 21. ábrán a kapcsolatot grafikusan is ábrázolhatja (1.6. ábra).
Rizs. 1.6. Két elem összekapcsolása
Rendszer nevezzük egy olyan elemkészletet, amely a következő tulajdonságokkal rendelkezik:
a) linkek, amelyek a rajtuk lévő elemről elemre történő átmenetek révén lehetővé teszik a halmaz bármely két elemének összekapcsolását;
b) a halmaz egyes elemeinek tulajdonságaitól eltérő tulajdonság (cél, funkció).
Nevezzük a jellemzőt a) rendszerkapcsolatnak, b) - funkciójának. A rendszer úgynevezett "tuple" (azaz felsorolás formájában megjelenő sorozat) definícióját alkalmazva írhatunk
ahol Σ a rendszer; ( M} – benne lévő elemek halmaza; ( x) - hivatkozások halmaza; F - a rendszer funkciója (új tulajdonsága).
A rekordot a rendszer legegyszerűbb leírásának tekintjük.
Szinte minden tárgy egy bizonyos nézőpontból rendszernek tekinthető. Fontos tisztában lenni azzal, hogy egy ilyen nézet hasznos-e, vagy bölcsebb-e megfontolni ezt a tárgyat elem. Tehát a rendszer rádiótechnikai táblának tekinthető , a bemeneti jelet a kimenetre konvertálni. Az elembázis specialistája számára a rendszer egy csillámkondenzátor lesz ebben a táblában, a geológusnak pedig - és maga a csillám, amely meglehetősen bonyolult szerkezettel rendelkezik.
Nagy rendszer nevezzünk olyan rendszert, amely jelentős számú azonos típusú elemet és azonos típusú kapcsolatokat tartalmaz.
Összetett rendszer nevezzünk olyan rendszert, amely különböző típusú elemekből áll, és közöttük heterogén kapcsolat van.
Gyakran csak egy nagyot tekintenek összetett rendszernek. Az elemek heterogenitása írással hangsúlyozható
Egy nagy, de mechanikailag nem bonyolult rendszer egy rudakból vagy például egy gázvezetékből összeállított daru gém. Ez utóbbi elemei a hegesztési varratok vagy támasztékok közötti szakaszok lesznek. Az elhajlás számításánál a gázvezeték elemeit valószínűleg viszonylag kis (körülbelül egy méteres) csőszakaszoknak tekintik. Ez a jól ismert végeselem módszerrel történik. Ebben az esetben a kapcsolat hatalmi (energetikai) jellegű - minden elem a szomszédosra hat.
A rendszer, a nagy rendszer és az összetett rendszer közötti különbségtétel önkényes. Tehát az első pillantásra homogének rakéták vagy hajók testét általában összetett rendszernek nevezik a különböző típusú válaszfalak jelenléte miatt.
A komplex rendszerek fontos osztálya az automatizált rendszerek. Az „automatizált” szó egy személy részvételét, tevékenységének rendszeren belüli felhasználását jelöli a technikai eszközök jelentős szerepének megőrzése mellett. Tehát egy műhely, egy szakasz, egy szerelvény lehet automatizált és automatikus („automatikus műhely”). Egy összetett rendszer esetében az automatizált mód előnyösebb. Például egy ember által támogatott repülőgép leszállása, míg az autopilótát általában csak viszonylag egyszerű mozgásokhoz használják. Jellemzőek azok a helyzetek is, amikor a műszaki eszközökkel kidolgozott megoldást személy jóváhagyja a kivitelezésre.
Így, automatizált rendszer komplex rendszernek nevezzük, melynek meghatározó szerepe kétféle elemből áll: a) technikai eszközök formájában; b) emberi cselekvések formájában. Szimbolikus jelölése (vö. és
ahol M T – technikai eszközökkel, mindenekelőtt számítógépek; M H - döntések és egyéb emberi tevékenységek; M"- a rendszer többi eleme.
Összesen ( x) ebben az esetben az ember és a technológia közötti összefüggések megkülönböztethetők ( x T - H}.
A szerkezet egy rendszert elemcsoportokra való felosztásának nevezzük, feltüntetve a köztük lévő kapcsolatokat, változatlan a mérlegelés teljes ideje alatt, és képet ad a rendszer egészéről.
Ennek a felosztásnak lehet anyagi (valódi), funkcionális, algoritmikus és egyéb alapja. A szerkezet elemcsoportjait általában a különböző csoportok elemei közötti egyszerű vagy viszonylag gyengébb kapcsolatok elve alapján különböztetjük meg. Célszerű a rendszer felépítését grafikus diagram formájában ábrázolni, amely cellákból (csoportokból) és az őket összekötő vonalakból (hivatkozásokból) áll. Az ilyen sémákat strukturálisnak nevezzük.
A szerkezet szimbolikus felírásához elemgyűjtemény helyett bevezetjük ( M), elemcsoportok halmaza ( M*) és e csoportok közötti kapcsolatok halmaza ( x * Ekkor a rendszer felépítése így írható fel
A szerkezetet az elemek csoportokba foglalásával kaphatjuk meg. Vegye figyelembe, hogy a funkció (cél) F rendszer kimaradt.
Mondjunk példákat a szerkezetekre. Egy előregyártott híd anyagszerkezete a helyszínen összeállított egyedi szakaszokból áll. Egy ilyen rendszer durva blokkdiagramja csak ezeket a szakaszokat és a csatlakoztatás sorrendjét jelzi. Ez utóbbi a kapcsolat, amely itt erõteljes természetû. A funkcionális szerkezetre példa a belső égésű motor felosztása energiaellátó, kenő-, hűtési, nyomaték-átviteli rendszerekre stb. Egy olyan rendszerre, ahol az anyagi és a funkcionális struktúrák egyesülnek, egy tervezőintézet különböző részlegei vannak. ugyanazon probléma oldalai.
Egy tipikus algoritmikus struktúra egy algoritmus (diagram) szoftver eszköz cselekvési sorrendet jelezve. Az algoritmikus struktúra egy olyan utasítás is lesz, amely meghatározza a műszaki objektum hibás működésének észlelésekor végrehajtandó műveleteket.
1.6. Az összetett objektumok tanulmányozását célzó mérnöki kísérlet főbb szakaszai
Ismertesse meg egy összetett objektumok tanulmányozását célzó mérnöki kísérlet főbb szakaszait.
1. A modell fizikai alapjainak felépítése.
A modell fizikai alapjainak felépítése, amely lehetővé teszi az ellenőrzés minőségét meghatározó leglényegesebb folyamatok kiemelését, valamint a determinisztikus és statisztikai komponensek arányának meghatározását a megfigyelt folyamatokban. A modell fizikai alapja egy összetett objektum "tervezésének" felhasználásával épül fel a vizsgált objektum leírására használt különböző tématerületeken. Minden témakör meghatározza saját rendszerek az objektum lehetséges „mozgásának” korlátozása. Ezen korlátok összességének figyelembe vétele lehetővé teszi a használt modellek komplexumának alátámasztását és konzisztens modell felépítését.
A modell „keretének”, azaz fizikai alapjának felépítése a vizsgált objektumot jellemző kapcsolatrendszer leírására redukálódik, különös tekintettel a megmaradási törvényekre és a folyamatok kinetikájára. Az objektumot jellemző összefüggésrendszer elemzése lehetővé teszi a folyamatok megfigyelt viselkedését elindító mechanizmusok térbeli és időbeli skálájának meghatározását, a statisztikai elem folyamatleíráshoz való hozzájárulásának minőségi jellemzését, valamint hogy feltárjuk a megfigyelt idősorok alapvető heterogenitását (ha létezik!).
A „keretrendszer” felépítése a külső és belső destabilizáló tényezők és a rendszer hatékonysága közötti ok-okozati összefüggések a priori adatainak megállapítására redukálódik, és ezen összefüggések kvantitatív becsléseit az objektumon végzett kísérletek konkretizálják. . Így garantált a kapott eredmények általánossága az objektumok egész osztályára vonatkozóan, konzisztenciája a korábban megszerzett ismeretekkel, valamint a kísérleti kutatások mennyiségének csökkentése. A modell „keretét” olyan strukturális-fenomenológiai megközelítéssel kell felépíteni, amely egyesíti a tárgy tanulmányozását a „külső” hatásokra adott reakcióival és a kutatás tárgya belső szerkezetének feltárásával.
2. A megfigyelési eredmények statisztikai stabilitásának ellenőrzése és a szabályozott változók változásának természetének meghatározása.
A statisztikai stabilitás empirikus alátámasztása a mintanagyság növekedésével az empirikus átlag stabilitásának vizsgálatára redukálódik (hosszabbító sorozat séma). A kísérleti úton kapott értékek kiszámíthatatlansága, mint ismeretes, nem szükséges és nem is elégséges feltétele a valószínűségelméleti fogalmak alkalmazásának. A valószínűségelmélet alkalmazásának szükséges feltétele a kezdeti mennyiségek átlagolt jellemzőinek stabilitása. Ezért a statisztikai robusztusság empirikus indukcióját alkalmazó tesztre van szükség n-az eredeti valószínűségi változó dimenziós empirikus eloszlásfüggvénye és valószínűségi eloszlása mintabecslésekhez.
3. Hipotézisek felállítása és tesztelése a vizsgált objektum "mozgásának" szerkezetére és paramétereire vonatkozóan.
Vegyük észre, hogy a statisztikai megközelítés megválasztásának oka általában a megfigyelt folyamat szabálytalansága, kaotikus jellege és éles törései. Ebben az esetben a kutató nem tudja vizuálisan észlelni a mintázatokat a megfigyelések sorozatában, és azt egy véletlenszerű folyamat megvalósításaként érzékeli. Ezt hangsúlyozzuk jön a legegyszerűbb minták kimutatásáról, hiszen az összetett minták kimutatása a megfigyelési eredmények irányított matematikai feldolgozását igényli.
4. A kimeneti változók előrejelzése a determinisztikus és statisztikai komponensek végeredményhez való hozzájárulásának figyelembevételével történik.
Vegye figyelembe, hogy csak a statisztikai megközelítés alkalmazása az előrejelzéshez komoly nehézségekbe ütközik. Először is, ahhoz, hogy döntéseket hozhassunk az aktuális veszteségek minimalizálásáról, nem azt kell tudni, hogy a folyamat átlagosan hogyan alakul, hanem azt, hogy egy adott időn belül hogyan fog viselkedni. Másodszor, általános esetben egy nem stacionárius, véletlenszerű folyamat előrejelzésének problémája van, változó matematikai elvárással, varianciával és az eloszlási törvény alakjával.
5. Az objektum szabályozási jellemzőinek és a vezérlőrendszer várható hatékonyságának felmérésére irányuló számítási kísérlet tervezése és megvalósítása.
A komplex rendszerek szerkezetének szintetizálásának problémái csak a legegyszerűbb esetekben oldhatók meg analitikusan. Ezért szükség van a tervezett rendszer elemeinek imitációs modellezésére (MI).
Az IM egy speciális módszer az összetett szerkezetű objektumok tanulmányozására, amely az objektum egyes elemeinek összes bemeneti és kimeneti változójának numerikus reprodukálásából áll. Az IM lehetővé teszi, hogy a struktúra elemzésének és szintézisének szakaszában ne csak a rendszer elemei közötti statisztikai kapcsolatokat vegyük figyelembe, hanem a működésének dinamikus vonatkozásait is.
Az IM elkészítéséhez a következőket kell tennie:
- a modellezés tárgyában kiválasztani azokat a legegyszerűbb elemeket, amelyekhez ismert a kimeneti változók számítási módja;
- az objektumban lévő elemek kapcsolódási sorrendjét leíró kommunikációs egyenletek felállítása;
- elkészíteni az objektum szerkezeti diagramját;
- válassza ki a modellezés automatizálásának eszközeit;
- IM programot kidolgozni;
- számítási kísérletek elvégzése az MI megfelelőségének, a szimulációs eredmények stabilitásának, valamint az MI vezérlés változásaira és zavaró hatásokra való érzékenységének felmérésére;
- a modell segítségével megoldani a vezérlőrendszer szintézisének problémáját.
A modellezés típusainak osztályozása különböző szempontok alapján történhet. A modellek számos jellemző alapján különböztethetők meg: a modellezett objektumok jellege, alkalmazási területei és a modellezés mélysége. Fontolja meg a 2 osztályozási lehetőséget. Az osztályozás első változata. A modellezési módszereket a modellezés mélysége szempontjából két csoportra osztják: anyagi (tárgy) és ideális modellezésre. Az anyagmodellezés egy tárgy és egy modell anyagi analógiáján alapul. Ezt a vizsgált tárgy alapvető geometriai, fizikai vagy funkcionális jellemzőinek reprodukálásával hajtják végre. A fizikai modellezés az anyagmodellezés speciális esete. Az analóg szimuláció a fizikai modellezés speciális esete. Különböző fizikai természetű, de ugyanazokkal a matematikai összefüggésekkel leírható jelenségek analógiáján alapul. Az analóg modellezésre példa a mechanikai rezgések (például egy rugalmas gerenda) vizsgálata ugyanazon differenciálegyenletekkel leírt elektromos rendszer segítségével. Mivel az elektromos rendszerrel végzett kísérletek általában egyszerűbbek és olcsóbbak, a mechanikai rendszer analógjaként vizsgálják (például hidak rezgésének vizsgálatakor).
Az ideális modellezés ideális (mentális) analógián alapul. A közgazdasági kutatásban (on magas szint megvalósításuk, és nem az egyes vezetők szubjektív vágyai alapján) a modellezés fő típusa. Az ideális modellezés viszont két alosztályra oszlik: jel (formalizált) és intuitív modellezés. A jelmodellezésben a modellek diagramok, grafikonok, rajzok, képletek. A jelmodellezés legfontosabb típusa a matematikai modellezés, amelyet logikai és matematikai konstrukciók segítségével hajtanak végre.
Az intuitív modellezés a tudomány és a gyakorlat azon területein található meg, ahol a kognitív folyamat kezdeti szakaszban van, vagy nagyon összetett rendszerszintű kapcsolatok állnak fenn. Az ilyen tanulmányokat gondolatkísérleteknek nevezik. A közgazdaságtan főként szimbolikus vagy intuitív modellezést alkalmaz; leírja a tudósok világképét vagy a dolgozók gyakorlati tapasztalatait az irányítás terén. A második osztályozási lehetőség az ábrán látható. 1.3 A teljesség osztályozási kritériumának megfelelően a modellezést teljesre, hiányosra és közelítőre osztják. Teljesen szimulálva a modellek időben és térben azonosak az objektummal. Hiányos szimulációk esetén ez az azonosság nem marad meg. A közelítő modellezés a hasonlóságon alapul, amelyben a valós objektum egyes aspektusait egyáltalán nem modellezik. A hasonlóságelmélet azt állítja, hogy az abszolút hasonlóság csak akkor lehetséges, ha az egyik tárgyat egy másik pontosan ugyanolyan objektum helyettesíti. Ezért a modellezés során abszolút hasonlóság nem következik be. A kutatók arra törekednek, hogy a modell csak a rendszer vizsgált aspektusát tükrözze jól. Például a diszkrét információátviteli csatornák zajtűrésének felmérésére a funkcionális ill információs modellek rendszereket nem lehet megtervezni. A modellezés céljának eléréséhez a feltételes valószínűségek mátrixával leírt eseménymodellt || рij || a j-edik ábécé i-edik karakterének átmenetei A médium típusától és a modell aláírásától függően a következő modellezési típusokat különböztetjük meg: determinisztikus és sztochasztikus, statikus és dinamikus, diszkrét, folytonos és diszkrét-folytonos . A determinisztikus modellezés olyan folyamatokat jelenít meg, amelyekben feltételezzük a véletlen hatások hiányát. A sztochasztikus modellezés számításba veszi a valószínűségi folyamatokat és eseményeket. A statikus modellezés az objektum állapotának leírására szolgál egy meghatározott időpontban, a dinamikus modellezés pedig az objektum időbeni tanulmányozására. Ugyanakkor működnek analóg (folyamatos), diszkrét és vegyes modellekkel. A hordozó megvalósítási formájától függően a modellezést mentálisra és valósra osztják. Mentális modellezést akkor alkalmazunk, ha a modellek adott időintervallumban nem valósíthatók meg, vagy annak nincsenek feltételei fizikai teremtés(például a mikrovilág helyzete). A valós rendszerek mentális modellezése vizuális, szimbolikus és matematikai formában valósul meg. Jelentős számú eszközt és módszert fejlesztettek ki az ilyen típusú modellezés funkcionális, információs és eseménymodelljei megjelenítésére. A valós tárgyakról alkotott emberi elképzeléseken alapuló vizuális modellezéssel vizuális modellek jönnek létre, amelyek tükrözik az objektumban előforduló jelenségeket és folyamatokat. Ilyen modellek például az oktatási plakátok, képek, diagramok, diagramok. A hipotetikus modellezés egy valós objektumban zajló folyamat szabályszerűségére vonatkozó hipotézisen alapul, amely tükrözi a kutatónak az objektumról való tudásának szintjét, és az objektum bemenete és kimenete közötti ok-okozati összefüggéseken alapul. tanulmányozás alatt. Ezt a fajta modellezést akkor használják, ha az objektum ismerete nem elegendő a formális modellek felépítéséhez.
A dinamikus modellezés egy többlépcsős folyamat, minden lépés megfelel a gazdasági rendszer viselkedésének egy bizonyos időszakra. Minden aktuális lépés megkapja az előző lépés eredményeit, amely bizonyos szabályok szerint meghatározza az aktuális eredményt és adatokat generál a következő lépéshez.
Így egy dinamikus modell gyorsított módban lehetővé teszi egy komplex gazdasági rendszer, mondjuk egy vállalkozás fejlődésének tanulmányozását egy bizonyos tervezési időszak alatt, az erőforrás-ellátás (nyersanyag, személyi állomány, pénzügy, technológia) változásának feltételei mellett. az elért eredményeket mutassa be a vállalkozás adott időszakra vonatkozó megfelelő fejlesztési tervében.
A matematikai programozás dinamikus optimalizálási problémáinak megoldására létrehozták a modellek megfelelő osztályát, a dinamikus programozást, melynek alapítója a híres amerikai matematikus, R. Bellman lett. Ennek az osztálynak a problémájának megoldására egy speciális módszert javasolt az „optimalitás elvén”, amely szerint optimális megoldás feladatot úgy találjuk meg, hogy felosztjuk n szakaszok, amelyek mindegyike egy-egy változóhoz tartozó részproblémát jelent. A számítást úgy kell elvégezni, hogy az egyik részfeladat optimális eredménye a következő részfeladat kezdőadata legyen, figyelembe véve az egyenleteket és a köztük lévő kapcsolatra vonatkozó megszorításokat, az utolsónak az eredménye a teljes probléma. Ebben a kategóriában minden modellben közös, hogy az aktuális vezetői döntések „megjelennek” mind a közvetlenül a döntés időpontjában, mind az azt követő időszakokban. Ebből következően a legfontosabb gazdasági hatások különböző időszakokban jelentkeznek, nem csak egy időszakon belül. Az ilyen gazdasági következmények főszabály szerint azokban az esetekben bizonyulnak jelentősnek, amikor új tőkebefektetések lehetőségével, a termelési kapacitás növelésével vagy a személyzet e célból történő képzésével kapcsolatos vezetői döntésekről van szó. előfeltételek megteremtése a jövedelmezőség növelésére vagy a költségek csökkentésére a következő időszakokban.
A modellek jellemző alkalmazási területei dinamikus programozás a döntések meghozatalakor:
A készletek feltöltésének pillanatát és a feltöltési megbízás nagyságát meghatározó készletkezelési szabályok kidolgozása.
A termelés ütemezésének és a foglalkoztatás kiegyenlítésének elveinek kialakítása ingadozó termékkereslet mellett.
A szükséges alkatrészmennyiség meghatározása a drága berendezések hatékony használatának biztosítása érdekében.
A szűkös tőkebefektetések felosztása lehetséges új felhasználási irányok között.
A dinamikus programozás módszerével megoldott feladatokban a célfüggvény (optimalizált kritérium) értékét a teljes folyamatra az egyes értékek egyszerű összegzésével kapjuk meg. fi (x) ugyanazt a kritériumot külön lépésekben, azaz
Ha az f (x) kritérium (vagy függvény) rendelkezik ezzel a tulajdonsággal, akkor additívnak (additív) nevezzük.
Dinamikus programozási algoritmus
1. A kiválasztott lépésben beállítjuk (a kényszerfeltételek által meghatározott) a jellemző változó értékeinek halmazát. utolsó lépés, a rendszer lehetséges állapotai az utolsó előtti lépésben. Minden lehetséges állapothoz és a kiválasztott változó minden értékéhez kiszámítjuk a célfüggvény értékeit. Ezek közül az utolsó előtti lépés minden eredményéhez kiválasztjuk a célfüggvény optimális értékeit és a vizsgált változó megfelelő értékeit. Az utolsó előtti lépés minden kimenetelénél emlékezzünk a változó optimális értékére (vagy több értékre, ha több ilyen érték is van) és a célfüggvény megfelelő értékére. Megkapjuk és javítjuk a megfelelő táblázatot.
2. Áttérünk az optimalizálásra az előzőt megelőző szakaszban ("visszafelé" mozgás), megkeresve az új változó optimális értékét, a következő változók korábban talált optimális értékeit rögzítve. A célfüggvény optimális értéke a következő lépésekben (a következő változók optimális értékeivel) az előző táblázatból olvasható ki. Ha az új változó az első lépést jellemzi, akkor lépjen a 3. pontra. Ellenkező esetben megismételjük a 2. lépést a következő változóhoz.
H. Adott a feladatban szereplő kezdeti feltétel, az első változó minden lehetséges értékére kiszámítjuk a célfüggvény értékét. Kiválasztjuk az első változó optimális értékének megfelelő célfüggvény optimális értékét.
4. Az első változó ismert optimális értékével meghatározzuk a következő (második) lépés kezdeti adatait, és az utolsó táblázat szerint a következő (második) változó optimális értékét (értékeit).
5. Ha a következő változó nem jellemzi az utolsó lépést, akkor lépjen a 4. pontra. Ellenkező esetben lépjen a 6. tételre.
6. Kialakítjuk (kiírjuk) az optimális megoldást.
Felhasznált irodalom jegyzéke
1. Microsoft Office 2010. Egy önálló használati útmutató. Y. Stotsky, A. Vasziljev, I. Telina. Péter. 2011, - 432 p.
2. Figurnov V.E. IBM PC a felhasználó számára. Kiadó 7. sz. - M .: Infra-M, 1995.
3. Levin A. Önálló kézikönyv a számítógépen végzett munkához. M.: Tudás, 1998, - 624 p.
4. Informatika: műhely a munka technológiájáról személyi számítógép/ Szerk. prof. N.V. Makarova - M.: Pénzügy és statisztika, 1997 - 384p.
5. Informatika: Tankönyv / Szerk. prof. N.V. Makarova - M.: Pénzügy és Statisztika, 1997 - 768 p.
Hasonló információk.
Bevezetés
dinamikus modell matematikai
A dinamikus modell egy elméleti konstrukció (modell), amely egy objektum állapotának változását (dinamikáját) írja le. A dinamikus modell tartalmazhat szakaszok vagy fázisok leírását, vagy alrendszerek állapotdiagramját. Gyakran van matematikai kifejezése, és főleg a társadalomtudományokban (például a szociológiában) használják, amelyek dinamikus rendszerekkel foglalkoznak, de a tudomány modern paradigmája hozzájárul ahhoz, hogy ezt a modellt is rendelkezik széleskörű felhasználás kivétel nélkül minden tudományban, beleértve. természetben és műszakiban.
A gazdasági és matematikai modellek a gazdaságot fejlődésben írják le (szemben a statikusakkal, amelyek egy adott pillanatban jellemzik állapotát). A dinamikus modell felépítésének két módja van:
optimalizálás (a gazdasági fejlődés optimális pályájának kiválasztása sok lehetséges közül)
leíró jellegű, amelynek középpontjában az egyensúlyi pálya (vagyis a kiegyensúlyozott, kiegyensúlyozott növekedés) fogalma áll.
Dinamikus ágazatközi modellek, tervszámítások közgazdasági és matematikai modelljei, amelyek lehetővé teszik a termelés, a tőkebefektetések (valamint a tárgyi eszközök és termelőkapacitások üzembe helyezése) évenkénti meghatározását az anyagágakra vonatkozóan. összekapcsolásukban. A dinamikus szektorközi modellekben a tervezési időszak minden évére a „nettó” végtermék mennyisége és szerkezete (személyes és állami fogyasztás, forgótőke- és állami tartalékok felhalmozása, export-import egyensúly, a növekedéssel nem járó tőkebefektetések). a vizsgált időszak termelése), valamint az időszak eleji befektetett eszközök mennyisége és szerkezete. A dinamikus szektorközi modellekben a statikus interszektorális modellekben rejlő közvetlen költségek együtthatója mellett speciális együtthatók kerülnek bevezetésre, amelyek a tőkebefektetések anyagi szerkezetét jellemzik.
Az alkalmazott matematikai apparátus típusa szerint a dinamikus interszektorális modelleket egyensúlyi és optimális modellekre osztják. Az egyensúlyi dinamikus iparágak közötti modellek lineáris egyenletrendszerként és lineáris differenciál- vagy differenciálegyenletek formájában is bemutathatók. Az egyensúlyi dinamikus szektorközi modelleket a késleltetés (az építkezés megkezdése és a megépült létesítmény üzembe helyezése közötti időkülönbség) is megkülönbözteti. Az optimális dinamikus szektorközi modelleket egy bizonyos optimalitási kritérium jelenléte, a lineáris egyenletrendszer felváltása egyenlőtlenségi rendszerrel, valamint a munkaerőre és a természeti erőforrásokra vonatkozó speciális korlátozások bevezetése jellemzi.
A dinamikus fizikai és virtuális objektumok objektíven léteznek. Ez azt jelenti, hogy ezek az objektumok bizonyos törvényeknek megfelelően működnek, függetlenül attól, hogy egy személy ismeri és érti őket vagy sem. Például egy autó vezetéséhez egyáltalán nem szükséges tudni, hogyan működik a motor, mi történik benne, és ez miért okozza az autó mozgását, ha megnyomja a gázt vagy elfordítja a kormányt. De ha az ember nem autót kíván vezetni, hanem vezérlőrendszert tervez hozzá, akkor már feltétlenül szükséges a folyamatok dinamikájának ismerete és megértése.
A dinamikus objektumokat és azok lineáris modelljeit több mint két évszázada sok tudós és mérnök alaposan tanulmányozta és elemezte. E tanulmányok és elemzések eredményeit az alábbiakban minőségileg, koncentrált formában mutatjuk be, ahogyan azt a szerző érzékelteti. Ez mindenekelőtt a dinamikus rendszerek lineáris modelljére, osztályozására, tulajdonságaik leírására és konzisztencia tartományára vonatkozik.
Ezenkívül az alábbiakban a nemlineáris rendszerek néhány tulajdonságát tárgyaljuk. A szavak, a "dinamikus", "dinamikus" kifejezések szilárdan és széles körben bekerültek az emberi tudás különböző területeibe, a mindennapi életben a szó tágabb értelmében vett energikus mozgás érzelmi jelzőjeként, a gyors változások szinonimájaként használatosak. A javasolt műben a „dinamikus” kifejezést szűk és közvetlen jelentésében fogjuk használni, ami „erőt”, azaz „erőt” jelent. a dinamikus objektum olyan tárgy, amely külső hatásoknak van kitéve, ami a szó legtágabb értelmében mozgáshoz vezet.
1. Dinamikus modellek: fogalom, típusok
A dinamikus tárgy egy fizikai test, műszaki eszköz vagy olyan folyamat, amelynek vannak bemenetei, a külső hatások lehetséges alkalmazási pontjai, és ezeket a hatásokat érzékelve, és kimenetekkel, pontokkal, a fizikai mennyiségek értékei jellemzik a tárgy állapotát. Egy objektum úgy tud reagálni a külső hatásokra, hogy megváltoztatja belső állapotát és az állapotát jellemző kimeneti értékeket. A tárgyra gyakorolt hatás, reakciója általában idővel változik, megfigyelhető, pl. megfelelő műszerekkel mérhető. Az objektum belső szerkezete egymásra ható dinamikus elemekből áll.
Ha elolvassa és elgondolkodik a fenti laza definíción, láthatja, hogy különálló dinamikus objektum "tiszta" formájában, mint önmagában lévő dolog nem létezik: az objektum leírásához a modellnek 4 hatásforrást is tartalmaznia kell ( generátorok):
a környezet és a hatások táplálásának mechanizmusa
az objektumnak terekben kell kiterjesztése
időben működni
a modellben mérőeszközöknek kell lenniük.
A tárgyat érő becsapódás lehet valamilyen fizikai mennyiség: erő, hőmérséklet, nyomás, elektromos feszültség és egyéb fizikai mennyiségek vagy több mennyiség kombinációja, a reakció, a tárgy válasza az ütközésre, lehet mozgás a térben, pl. például elmozdulás vagy sebesség, hőmérséklet-változás, áramerősség stb.
A dinamikus objektumok lineáris modelljeinél érvényesül a szuperpozíció (overlay) elve, azaz. a hatások egy halmazára adott reakció egyenlő az mindegyikre adott reakciók összegével, és a hatás nagy léptékű változása megfelel az arra adott reakció arányos változásának. Egy hatás több objektumra vagy egy objektum több elemére is alkalmazható.
A dinamikus objektum fogalma tartalmazza és kifejezi a rá gyakorolt hatás és a válasz közötti ok-okozati összefüggést. Például egy hatalmas testre kifejtett erő és annak helyzete és mozgása, egy elemre adott elektromos feszültség és a benne folyó áram között.
Általános esetben a dinamikus objektumok nemlineárisak, beleértve a diszkrétséget is, például gyorsan megváltoztathatják a szerkezetet, amikor a cselekvés elér egy bizonyos szintet. De általában a működési idő nagy részében a dinamikus objektumok időben folytonosak, kis jeleknél pedig lineárisak. Ezért az alábbiakban a fő figyelmet a lineáris folytonos dinamikus objektumokra fordítjuk.
Folytonossági példa: autó az úton halad -időben folyamatosan működő tárgy, helyzete az időtől folyamatosan függ. Az idő nagy részében egy autót úgy lehet tekinteni, mint vonal objektum, lineáris üzemmódban működő objektum. És csak balesetek, ütközések esetén, amikor például egy autó megsemmisül, nemlineáris objektumként kell leírni.
Egy objektum kimeneti értékének linearitása és időbeni folytonossága csak egy kényelmes speciális, de fontos eset, amely lehetővé teszi egy dinamikus objektum jelentős számú tulajdonságának egyszerű figyelembevételét.
Másrészt, ha egy objektumot különböző időskálán zajló folyamatok jellemeznek, akkor sok esetben megengedhető és hasznos a cseréje. leggyorsabb folyamatok diszkrét időbeli változásuk.
Ezt a munkát elsősorban a dinamikus objektumok lineáris modelljeinek szenteljük determinisztikus hatások hatására. Tetszőleges típusú sima determinisztikus hatások generálhatók diszkrét, viszonylag ritka additív hatással a hatás alsó származékaira adagolt deltával -funkciókat. Az ilyen modellek összhangban vannak a valós objektumok nagyon széles osztályára vonatkozó viszonylag kis hatásokkal. Például így jönnek létre a vezérlőjelek számítógépes játékok autó vagy repülőgép vezérlésének szimulálása a billentyűzetről. A véletlen behatások továbbra is kívül esnek a mérlegelési körön.
Egy dinamikus objektum lineáris modelljének konzisztenciáját különösen az határozza meg, hogy a kimeneti értéke kellően sima, pl. hogy ez és több alacsonyabb idejű deriváltja folytonos-e. Az a tény, hogy a valós objektumok kimeneti értékei időben simán változnak. Például egy repülőgép nem tud azonnal mozogni a tér egyik pontjáról a másikra. Ráadásul, mint minden hatalmas test, nem tudja hirtelen megváltoztatni a sebességét, ehhez végtelen erőre lenne szükség. De egy repülőgép vagy autó gyorsulása hirtelen megváltozhat.
A dinamikus objektum fogalma egyáltalán nem határozza meg átfogóan a fizikai objektumot. Például, ha egy autót dinamikus objektumként ír le, megválaszolhatja azokat a kérdéseket, hogy milyen gyorsan gyorsul és lassul, milyen simán halad egyenetlen utakon és egyenetlenségeken, milyen hatásokat tapasztalnak az autó vezetője és utasai az úton történő vezetés során. , melyik hegyet tud megmászni stb. P. De egy ilyen modellnél nem mindegy, hogy milyen színű az autó, nem fontos az ára stb., amennyiben ezek nem befolyásolják az autó gyorsulását. A modellnek tükröznie kell a modellezett objektum fő tulajdonságait valamilyen kritérium vagy kritériumrendszer szempontjából, és figyelmen kívül kell hagynia a másodlagos tulajdonságait. Ellenkező esetben túl bonyolult lesz, ami megnehezíti a kutatót érdeklő tulajdonságok elemzését.
Másrészt, ha a kutatót pontosan az autó színének időbeli változása érdekli, amelyet különféle tényezők, például napfény vagy öregedés okoz, akkor erre az esetre a megfelelő differenciálegyenlet felállítható és megoldható.
A valós tárgyak, valamint elemeik, amelyek dinamikus objektumnak is tekinthetők, nem csak érzékelnek egy bizonyos forrásból származó hatásokat, hanem maguk is hatnak erre a forrásra, ellensúlyozzák azt. A vezérelt objektum kimeneti értéke sok esetben egy másik, következő dinamikus objektum bemenete, ami viszont az objektum működési módját is befolyásolhatja. Hogy. egy dinamikus objektum kapcsolatai a külvilággal, ahhoz képest kétirányúak.
Sok probléma megoldása során gyakran egy dinamikus objektum viselkedését csak időben veszik figyelembe, és a térbeli jellemzőit, ha azok közvetlenül nem érdeklik a kutatót, nem veszik figyelembe és nem veszik figyelembe, kivéve a jel késleltetésének egyszerűsített figyelembevétele, amely az ütközés terjedési idejéből adódhat.a térben a forrástól a vevőig.
A dinamikus objektumokat differenciálegyenletek (differenciálegyenlet-rendszer) írják le. Sok gyakorlatilag fontos esetben ez egy lineáris, közönséges differenciálegyenlet (ODE) vagy egy ODE rendszer. A dinamikus objektumok típusainak sokfélesége meghatározza a differenciálegyenletek nagy jelentőségét, mint a leírásukra szolgáló univerzális matematikai apparátus, amely lehetővé teszi ezen objektumok elméleti kutatását (elemzését), és az ilyen elemzések alapján modellek megalkotását. és az emberek számára hasznos rendszereket, eszközöket, eszközöket építeni, a körülöttünk lévő világ szerkezetének magyarázatára, legalábbis a makrokozmosz (nem mikro- és nem mega-) léptékében.
Egy dinamikus objektum modellje akkor konzisztens, ha megfelelő, megfelel egy valós dinamikus objektumnak. Ez a megfeleltetés egy bizonyos térbeli-időbeli területre és hatástartományra korlátozódik.
A dinamikus objektummodell megvalósítható, ha meg tud építeni valódi tárgy, amelynek viselkedése cselekvések hatására egy bizonyos tér-idő tartományban és a bemeneti műveletek egy bizonyos osztályára és tartományára megfelel a modell viselkedésének.
Az osztályok szélessége, a dinamikus objektumok struktúráinak sokfélesége ahhoz a feltételezéshez vezethet, hogy ezek együttesen számtalan tulajdonsággal rendelkeznek. Azonban egy kísérlet e tulajdonságok, valamint a dinamikus objektumok működési elveinek megragadására és megértésére, a maguk sokféleségében, egyáltalán nem olyan reménytelen.
A helyzet az, hogy ha a dinamikus objektumokat a differenciálegyenletek megfelelően leírják, és ez pontosan így van, akkor egy bármilyen típusú dinamikus objektumot jellemző tulajdonságkészletet a differenciálegyenletét jellemző tulajdonságok halmaza határozza meg. Elmondható, hogy legalábbis a lineáris objektumok esetében meglehetősen korlátozott és viszonylag kis számú ilyen alapvető tulajdonság létezik, ezért a dinamikus objektumok alapvető tulajdonságainak halmaza is korlátozott. Ezekre a tulajdonságokra alapozva és az ezeket birtokló elemek kombinálásával dinamikus objektumokat hozhat létre sokféle jellemzővel.
Tehát a dinamikus objektumok fő tulajdonságai elméletileg differenciálegyenleteikből származnak, és korrelálnak a megfelelő valós objektumok viselkedésével.
Dinamikus objektum -olyan objektum, amely érzékeli az időben változó külső hatásokat, és a kimeneti érték megváltoztatásával reagál rájuk. Az objektum belső szerkezete egymásra ható dinamikus elemekből áll. Az objektumok hierarchiáját alulról a legegyszerűbb modellek korlátozzák, és azok tulajdonságain alapul.
A tárgyra gyakorolt hatás, valamint reakciója fizikai, mérhető mennyiség, lehet fizikai mennyiségek halmaza is, matematikailag vektorokkal leírva.
Amikor a dinamikus objektumokat differenciálegyenletekkel írjuk le, hallgatólagosan azt feltételezzük, hogy a dinamikus objektum minden eleme annyi energiát (ilyen energiát) kap és fogyaszt, amennyi a rendeltetésének megfelelően a normál működéshez szükséges, válaszul a bejövő hatásokra. Az objektum ennek az energiának egy részét a bemeneti műveletből kaphatja, és ezt a differenciálegyenlet kifejezetten leírja, a másik része származhat harmadik féltől származó forrásokés nem jelennek meg a differenciálegyenletben. Ez a megközelítés nagyban leegyszerűsíti a modell elemzését anélkül, hogy torzítaná az elemek és a teljes objektum tulajdonságait. Ha szükséges, a külső környezettel való energiacsere folyamata részletesen leírható explicit formában, és ezek is differenciál- és algebrai egyenletek lesznek.
Egyes speciális esetekben az objektum kimenőjelének minden energia (teljesítmény) forrása a bemeneti művelet: egy kar, egy hatalmas test erővel történő gyorsítása, passzív elektromos áramkör satöbbi.
Általános esetben a hatást úgy tekinthetjük, mint az energiaáramlás szabályozását a kimenő jel szükséges teljesítményének eléréséhez: szinuszos jel erősítője, ideális erősítő stb.
A dinamikus objektumok – akárcsak dinamikus objektumnak is tekinthető elemeik – nemcsak érzékelik a hatást annak forrásából, hanem maguk is hatnak erre a forrásra: például a klasszikus mechanikában ezt a Newton harmadik törvényében megfogalmazott elv fejezi ki. : a hatás egyenlő a reakcióval, az elektrotechnikában a forrásfeszültség a forrás és a terhelés közötti dinamikus egyensúly eredménye. Hogy. egy dinamikus objektum kapcsolatai a külvilággal, ahhoz képest kétirányúak.
Lényegében egy dinamikus objektum minden eleme kétirányú, akárcsak maga az objektum a külső objektumokhoz képest. Ez Newton harmadik, általa a mechanika számára megfogalmazott törvényének általánosításából következik: egy test ellenereje egyenlő a másik test által rá ható erővel, és arra irányul, és a kémiában is a formában fogalmazódik meg. Le Chatelier elvének. Összefoglalva azt mondhatjuk, hogy az egyik dinamikus elem hatása a másikra találkozik valamiféle ellenállással. Például egy feszültségforrás elektromos terhelése ellentétes az árammal, megváltoztatva a feszültség értékét a forrás kimenetén. Általános esetben a terhelés ellenhatása befolyásolja a forrás működési módját, és viselkedésüket ennek eredményeként lehetőség szerint valamilyen dinamikus egyensúlyba való átmenet határozza meg.
Sok esetben a hatásforrás teljesítménye sokkal nagyobb, mint a dinamikus objektum vevőjének szükséges bemeneti teljesítménye. Ebben az esetben a dinamikus objektum gyakorlatilag nem befolyásolja a forrás (generátor) működési módját, és a kapcsolat a forrástól az objektumig egyirányúnak tekinthető. Egy elem ilyen egyirányú modellje, amely egy objektum racionális fizikai strukturálásán alapul, nagyban leegyszerűsíti a rendszer leírását és elemzését. Valójában sok műszaki objektum, bár messze nem mindegyik, pontosan ennek az elvnek megfelelően épül fel, különösen a vezérlési problémák megoldására szolgáló rendszerek tervezésekor. Más esetekben, például egy probléma megoldásánál, amikor a motor maximális hatásfokának elérése szükséges, nem elhanyagolható az ellenkezés.
Egy dinamikus objektum szerkezetének részletezésével el lehet jutni az elemi, hagyományosan nem egyszerűsített objektumokhoz. Az ilyen objektumokat a legegyszerűbb algebrai és differenciálegyenletek írják le. Valójában az ilyen elemek összetett szerkezetűek is lehetnek, de a modellezés során kényelmesebb egyetlen egészként felfogni őket, amelynek tulajdonságait ezek a viszonylag egyszerű egyenletek határozzák meg, amelyek a reakciót összekapcsolják az ütközéssel.
1.1 Fizikai modellek
Ez egy objektum vagy rendszer kinagyított vagy kicsinyített leírásának neve. A fizikai modell sajátossága, hogy bizonyos értelemben modellezett integritásnak tűnik.
A fizikai modell leghíresebb példája egy épülő repülőgép másolata, amely az arányok teljes tiszteletben tartásával készült, mondjuk 1:50 arányban. Az új tervezésű repülőgép fejlesztésének egyik szakaszában szükségessé válik az alapvető aerodinamikai paraméterek ellenőrzése. Ebből a célból az elkészített példányt egy speciális (szélcsatornában) átfújják, majd a kapott leolvasást alaposan megvizsgálják. Ennek a megközelítésnek az előnyei egyértelműek. Éppen ezért az összes vezető repülőgépgyártó minden új repülőgép fejlesztésénél alkalmaz ilyen típusú fizikai modelleket.
A többemeletes épületek kisebb példányait gyakran szélcsatornában helyezik el, szimulálva az építési területre jellemző szélrózsát. Fizikai modelleket is használnak a hajógyártásban.
1.2 Matematikai modellek
Ez azoknak a modelleknek a neve, amelyek matematikai szimbólumokat és módszereket használnak egy objektum vagy esemény tulajdonságainak és jellemzőinek leírására. Ha egy probléma átvihető a képletek nyelvére, akkor az nagyon leegyszerűsödik. A matematikai megközelítés azért is egyszerű, mert jól meghatározott merev szabályoknak engedelmeskedik. ,amely rendelettel vagy más módon nem törölhető. Életünk összetettsége éppen abban rejlik, hogy sok, ami benne történik, gyakran mentes a konvencióktól. A matematika a jelenségek leegyszerűsített leírásával foglalkozik. Lényegében bármely képlet (vagy képletkészlet) a konstrukció egy bizonyos szakaszát képviseli matematikai modell... A tapasztalat azt mutatja, hogy meglehetősen egyszerű modellt építeni (egyenletet írni). Ebben a modellben és ezért leegyszerűsített formában nehéz átadni a vizsgált jelenség lényegét.
A valós tárgy bármely funkcionális elemének megvan a maga szerkezete, az egész objektumhoz hasonlóan mentálisan vagy fizikailag kölcsönható elemekre osztható. Az elemi dinamikus objektum egy valós objektum racionálisan kiválasztott eleme, amelyet hagyományosan oszthatatlannak tekintünk, és amely összességében rendelkezik valamilyen alapvető tulajdonsággal, például tehetetlenséggel, és a legegyszerűbb algebrai vagy differenciálegyenlettel leírható pontossággal.
A dinamikus objektumok legfontosabb, alapvető tulajdonsága a tehetetlenségük. Fizikailag a tehetetlenség abban nyilvánul meg, hogy a tárgy nem azonnal, hanem fokozatosan reagál a külső hatásokra, és külső hatások hiányában igyekszik fenntartani állapotát és viselkedését. Matematikailag a tehetetlenség abban fejeződik ki, hogy egy valós objektum kimeneti értéke időben folytonos. Sőt, a kibocsátott mennyiség egyes alacsonyabb deriváltjainak is folytonosnak kell lenniük, nem változhatnak ugrásszerűen korlátozott teljesítményű hatások hatására, beleértve a hirtelen, időben változókat is.
A legegyszerűbb inerciális dinamikus objektumok -kinedin .Ezek olyan elemi tárgyak, amelyek mentálisan vagy fizikailag el vannak szigetelve egy összetett objektum szerkezetétől, és kellő pontossággal engedelmeskednek a legegyszerűbb, különböző rendű differenciálegyenleteknek. Az ilyen modellek konzisztensek, legalábbis bizonyos tér-idő tartományban és a jelnagyságok korlátozott tartományában.
Egy dinamikus objektum, egy bizonyos differenciálegyenletnek megfelelő objektum tehetetlenségének matematikai leírása az, hogy az ütközés közvetetten befolyásolja az objektum reakcióját, közvetlenül befolyásolja a reakció egyik vagy másik deriváltját az idő függvényében, vagy több őket egyszerre. Ez ahhoz a tényhez vezet, hogy a reakció csak idővel nyilvánul meg.
Valóban, egy ilyen leírás megfelel a valós tárgyak viselkedésének. Például néhány, viszonylag kicsi pillanatnyi betáplálásával, amely nem változik, miután egy másodrendű elemi objektumra ütést, például egy tehetetlenségi tömegre ható erőt fejt ki, a tárgy egy ideig, bár kis ideig megmarad. ugyanabban az állapotban, mint a betáplálás előtt, ugyanolyan sebességgel rendelkezik, mint korábban.
De a második származék, i.e. gyorsulás, hirtelen ugrik, arányosan a kifejtett erő nagyságával. És ezért csak az idő múlásával, és nem azonnal, a második derivált jelenléte a sebesség változásában, tehát a későbbiekben és a test térbeli helyzetében nyilvánul meg.
1.3 Analóg modellek
Ez egy olyan modell neve, amely a vizsgált objektumot analógként ábrázolja, amely valódi objektumként viselkedik, de nem úgy néz ki.
Íme két meglehetősen tipikus példa.
1. példa Az erőfeszítés és az eredmények közötti kapcsolatot szemléltető grafikon egy analóg modell. ábrán látható grafikon. Az 1.1 megmutatja, hogy a hallgatónak a vizsgára való felkészüléséhez szükséges idő hogyan befolyásolja az eredményt.
Rizs. 1.1. Az erőfeszítés és az eredmények kapcsolatát bemutató grafikon
2. példa Tegyük fel, hogy meg kell találnia a leggazdaságosabb módot a rendszeres ismert áruszállításokhoz három városba, ehhez csak egy raktárt kell építeni. A fő követelmény: a raktár helyének olyannak kell lennie, hogy az összes szállítási költség a legalacsonyabb legyen (úgy kell tekinteni, hogy az egyes szállítások költsége megegyezik a raktár és a rendeltetési hely közötti távolság és a raktár össztömegének szorzatával. szállított áruk és tonnakilométerben mérik).
A terület térképét egy rétegelt lemezre ragasztjuk. Ezután minden város helyén lyukakat vágunk át, szálakat vezetünk át rajtuk, és a város áruigényével arányos súlyokat rögzítünk hozzájuk (1.2. ábra). Kösse össze a szálak szabad végeit egy csomóba, és engedje el. A gravitáció hatására a rendszer egyensúlyi állapotba kerül. A rétegelt lemez lapon a csomópont által elfoglalt hely, amely megfelel a raktár optimális helyének (1.3. ábra).
Megjegyzés. Az egyszerűség kedvéért nem vesszük figyelembe azon utak költségeit, amelyeket át kell építeni.
Rizs. 1.2. Tereptérkép egy rétegelt lemez lapon
Rizs. 1.3. Optimális raktári elhelyezkedés
2. Diszkrét objektumok matematikai modelljeinek felépítése
2.1 Populációs modell
Érdekes módon a matematikai modell felépítése gyakran egyáltalán nem nehéz. Ehhez gyakran a legegyszerűbb és legkönnyebben megmagyarázható feltételezéseket alkalmazzák. Leírjuk, hogyan lehet ezt megtenni egy szinte valós példa segítségével. Képzeljük el a következő képet. 18. század közepe Közép-Európa ,tartományi plébánia, templom, plébánosok - a környező falvak lakói, a plébános észreveszi, hogy a templom szűk lett az istentiszteletre: nőtt a plébánosok száma. A plébános elmélkedik: ha a jövőben tovább növekszik a plébánosok száma, akkor új templomot kell építeni, amihez jelentős pénzre lesz szükség.
A pap tisztában van azzal, hogy a templom építésének ideje és mérete nagyban függ attól, hogy a környező lakók száma hogyan változik. És úgy dönt, hogy megpróbálja kiszámítani. Próbáljuk meg, és a modern elnevezések és nyelvezet segítségével megfogalmazzuk érvelésének lehetséges menetét.
Jelöljük x-szel a plébánosok számát az n-edik év végére. Számuk egy évben, i.e. az (n + 1) év végére természetes, hogy x-szel jelöljük n + 1 .Ekkor az idei szám változása a különbséggel írható le
Két természetes okból következik be - emberek születnek és meghalnak (az egyszerűség kedvéért feltételezzük, hogy a migrációs vírus akkor még nem érte el ezt a területet). A születések és az elhalálozások évenkénti számát plébániai könyvek segítségével nem nehéz meghatározni. Megszámolva a születések és elhalálozások számát a különböző években, a pap úgy dönt, hogy a kapott számokat és d1, ..., dk összehasonlítja az összes plébánosok számával ezekben az években x1, .., xk, és észreveszi, hogy az arányok x1, ..., xk az évektől nagyon kevéssé különböznek. Ugyanez vonatkozik a kapcsolatokra is.
A számítások egyszerűsítése érdekében ezeket a kapcsolatokat állandónak tekintjük és jelöljük? és? illetőleg. Így a születések száma ben n-edik év egyenlőnek bizonyul, a halálozások száma xn, a természetes okokból bekövetkezett változás pedig + xn - xn.
Ennek eredményeként eljutunk az Xn = Xn - Xn relációhoz, vagy részletesebben:
xn + 1 = xn + Xn-xn
Tedd? = 1 +? -?. Ekkor a számunkra érdekes képlet alakot ölt
A modell megépült.
Most próbáljuk meg kitalálni, mi történt, vagyis elemezzük a felépített modellt. Három eset lehetséges:
1)?>1(?=?-?>0 -többen születnek, mint meghalnak) és a plébánosok száma évről évre nő,
2)?=1 (?=?-?=0 -annyian halnak meg, ahányan születnek) és a plébánosok száma évről évre változatlan,
3)?<0 (?=?-?<0 -többen halnak meg, mint ahányan születnek) és a plébánosok száma folyamatosan csökken.
Mivel a modell elkészítésének motivációja az volt, hogy megtudjuk, milyen gyorsan növekszik a plébánosok száma, kezdjük az 1. esettel.
1. eset. Tehát a plébánosok száma növekszik. De hogyan, milyen gyorsan? Itt az ideje, hogy röviden felidézzük a figyelmeztető történetet (szomorú példázatot) a sakk ismeretlen feltalálójáról. Azt mondják, hogy a játék nagyon tetszett a gazdag és mindenható maharadzsának, aki azonnal úgy döntött, hogy megjutalmazza a feltalálót, és nagylelkűen felajánlotta, hogy kiválasztja a jutalmat. Ahogy mondani szokás, miután lekefélte a figurákat a sakktábláról, egy búzaszemet tett az 1. cellára, a 2. -két szem, 3-án -négy szem, 4-én -nyolc szem (2.1. ábra), és azt javasolta a maharadzsának, hogy adjon parancsot a szolgáknak, hogy a javasolt törvény szerint szórják ki a búzaszemeket a sakktábla többi cellájára, azaz így: 1,2,4,8 ,16, ..., 263.
Rizs. 2.1. Sakktábla probléma és maharadzsa jutalom
Maharaj majdnem megsértette ezt az egyszerű kérést, és beleegyezett. hosszú időbe telik, amíg elkészül. De a feltaláló ragaszkodott hozzá. – parancsolta Maharaja. És a szolgák azonnal rohantak végrehajtani ezt a "fényt" gyakorlat. Mondanunk sem kell, hogy nem tudták végrehajtani a maharadzsa parancsát. Az a tény, hogy a búzaszemek teljes száma a sakktáblán egyenlőnek kellett volna lennie 2-vel 64 - 1,ami jóval magasabb, mint amit ma már az egész világon egy év alatt termesztenek. Nagyon röviden fejezzük be a példázatot: a maharadzsa ismeretlen helyzetbe került. -nyilvánosan ígéretet tett, és nem tudta teljesíteni. A tettest azonban azonnal megtalálták. Talán ezért nem őrizte meg a történelem a sakk feltalálójának nevét. Próbáljuk meg azonban grafikonon ábrázolni, hogy milyen gyorsan növekszik a szemcsék száma az egyes következő cellákban, a jobb áttekinthetőség érdekében a szomszédos pontokat összekötve (2.2. ábra).
Rizs. 2,2-2,3. Exponenciális népességváltozás
A sakk feltalálója által javasolt szabály X n + 1 = 2x n az (1) képlet speciális esete ?= 2, és ehhez hasonlóan leírja azt a törvényt, amelyet követve egy geometriai haladást alkotó számsort kapunk. Bármilyen ?>1x változását illusztráló kép n ,hasonló alakja van - x n exponenciálisan fog növekedni. 1820-ban Londonban T.R. Malthus megjelentette "A politikai gazdaságtan alapelvei gyakorlati alkalmazásuk szempontjából" című munkáját (orosz fordításban). -"Tapasztalatok a népesedés törvényéről..." T. 1-2. SPb., 1868), amelyben különösen elhangzott, hogy az emberek biológiai tulajdonságai miatt a populáció a geometriai progresszió törvénye szerint szaporodik,
x n = 1 =?x n, ?>1,
míg a megélhetési eszközök csak a számtani progresszió törvénye szerint növekedhetnek, y n + 1 = y n + d ,d> 0. Ez a különbség a mennyiségi változás mértékében közvetlenül összefügg a populáció túlélési problémáival (2.3. ábra) ,nem maradhatott észrevétlen, és elég kemény kritikát és erősen átpolitizált vitákat váltott ki az érintett körökben. Próbáljunk meg a kritika tényéből egy hasznos következtetést levonni a felépített modell megfelelőségéről (1). Természetesen a helyzet leírásának egyszerűsítésénél néhány körülményt figyelmen kívül kell hagyni, azokat jelentéktelennek tekinteni. Úgy tűnik azonban, hogy nincs egységes nézet arról, hogy mi a lényeges és mi nem. Nem lehet például figyelni arra, hogy elkezdődött az eső. De el kell ismerni, hogy egy dolog száz métert futni zuhogó esőben, és egészen más -egy óra séta ebben az esőben esernyő nélkül. Itt is hasonlót figyelünk meg: 3-4 évre előre számolva az (1) képlet elég jól működik, de az erre épülő hosszú távú előrejelzés hibásnak bizonyul.
Fontos következtetés. Amikor javaslatot tesz egy olyan modellre, amelyet megépít vagy választ, feltétlenül jeleznie kell, hogy milyen korlátokon belül használható, és figyelmeztetnie kell, hogy ezeknek a határoknak a megszegése súlyos hibákhoz vezethet (és valószínűleg az is). Röviden, minden modellnek megvan a maga erőforrása. Blúz vagy ing vásárlásakor megszoktuk a címkék jelenlétét, amelyek a megengedett legnagyobb vasalási hőmérsékletet, a megengedett mosási módokat stb. vasalni, hogy egyszer átmenjen rajta -egyéb az anyagon. Megteheted. De szeretne blúzt vagy inget viselni ilyen vasalás után? 2. eset. A populáció mérete nem változik (2.4. ábra). 3. eset. A populáció kihalóban van (2.5. ábra).
Rizs. 2.4. Népességi grafikon állandó populációval
Rizs. 2.5. Népességi grafikon csökkenő számokkal
Szándékosan részletesen foglalkoztunk a populációs modell leírásával, egyrészt azért, mert ez az egyik első ilyen modell, másrészt azért, hogy példáján keresztül bemutassuk, milyen fő állomásain van a népesedési modell felépítésének problémája. matematikai modell megy keresztül.
Megjegyzés 1. Ennek a populációs modellnek a leírásakor nagyon gyakran a differenciális változatára támaszkodunk: x =?x (itt x = x (t) -időfüggő népességnagyság, x " -idő derivált, ?-állandó).
Megjegyzés 2. Nagy x értékek esetén a létfenntartási forrásokért folyó versengés az érték csökkenéséhez vezet ?,és ezt a merev modellt le kell cserélni egy lágyabb modellre: x =?(x) x ,amelyben az együttható ?a lakosság nagyságától függ. A legegyszerűbb esetben ezt a függőséget a következőképpen írjuk le:
? (x) = a-bx
ahol a és b -konstans számok, és a megfelelő egyenlet alakját veszi fel
x = ax-bx 2
És elérkeztünk egy bonyolultabb, úgynevezett logisztikai modellhez, amely már elég jól leírja a népességdinamikát. A logisztikus görbe elemzése (2.6. ábra) tanulságos és érdekes lehet az olvasó számára. A logisztikai modell más folyamatokat is jól leír, például a reklámozás hatékonyságát.
Rizs. 2.6. Logisztikai görbe
2.2 A ragadozó-zsákmány modell
A fentiek a lakosság akadálytalan szaporodásáról szóltak. Valós körülmények között azonban egy populáció együtt él más populációkkal, és sokféle kapcsolatban van velük. Itt egy gyors pillantást vetünk az antagonista ragadozópárra -áldozat (lehet egy hiúzpár -nyúl és egy pár katicabogár -levéltetű), és próbálja nyomon követni, hogyan változhat a két interakcióban részt vevő fél száma idővel. A zsákmánypopuláció önállóan, míg a ragadozópopuláció csak a zsákmány rovására létezhet. Jelöljük a zsákmánypopuláció méretét x-en, a ragadozópopuláció méretét y-n keresztül. Ragadozó hiányában a zsákmány az x egyenlet szerint szaporodik = fejsze ,a> 0 ,és a ragadozó zsákmány hiányában a törvény szerint kihal y =-y ,?>0.A ragadozó minél több zsákmányt eszik meg, annál több és annál több. Ezért ragadozó jelenlétében a zsákmányszám a törvény szerint változik
x = fejsze- ? xy, ?>0
Az elfogyasztott zsákmány mennyisége hozzájárul a ragadozó szaporodásához, amit így írhatunk le: y =-y +xy , ?>0.
Így megkapjuk az egyenletrendszert
x = ax- xy
y = - y +xy
ráadásul x? 0, y? 0.
Predator modell -az áldozat épül.
Mint a korábbi modell, számunkra a leginkább érdekes az egyensúlyi pont (x *, y *), ahol x * és y * -nem nulla megoldása az egyenletrendszerre
ax-? xy =0
Y + xy =0
vagy x (a- y ) = 0, y (- ?+? x )=0
Ezt a rendszert mindkét populáció számának x = 0, y stabilitási feltételéből kapjuk =0
Az egyensúlyi pont koordinátái -ez a vonalak metszéspontja
a-? y =0 (2)
?+? x =0 (3)
könnyen kiszámítható:
, (2.7. ábra).
Rizs. 2.7. Egyenletrendszer megoldása
Az O (0,0) koordináták origója a (2) egyenlet által megadott vízszintes egyeneshez viszonyított pozitív félsíkban, a (3) egyenlet által adott függőleges egyeneshez képest pedig a negatív félsíkban található (ábra 2.8). Így az első negyed (és csak ez érdekel minket, mivel x> 0 és y> 0) négy régióra van osztva, amelyeket kényelmesen a következőképpen jelölünk: 1 - (+, +), 2 - (-, + ), 3- ( -, -), 4 - (+, -).
Rizs. 2.8. A megoldási tartomány felosztása kvadránsokra
Legyen a Q (x0, y0) kezdeti állapot a IV. Ekkor az egyenlőtlenségek? -? Y0> 0, -? +? X0<0? из которых следует, что скорости x" и у" в этой точке должны быть разных знаков, x>0, y<0 и, значит, величина х должна возрастать, а величина убывать.
Hasonló módon elemezve x és y viselkedését a 2., 3. és 4. tartományban, az ábrán látható képhez jutunk. 2.9.
Rizs. 2.9. X és y változtatása kvadránsokkal
Így a Q kezdeti állapot a zsákmány és a ragadozó számának periodikus ingadozásához vezet, így a rendszer egy idő után ismét Q állapotba tér vissza (2.10. ábra).
Rizs. 2.10. A ragadozók és a zsákmány számának ciklikus ingadozása
Amint a megfigyelések azt mutatják, egyszerűsége ellenére a javasolt modell minőségileg helyesen tükrözi a ragadozó-zsákmány rendszer abundanciájának oszcilláló jellegét (2.11. ábra).
Rizs. 2.11. A nyúl - hiúz és levéltetvek - katicabogár rendszerek rezgései
Valódi megfigyelések. Néha meglehetősen veszélyes beleavatkozni a természeti törvények olyan cselekedeteibe, amelyeket nem értünk. -a rovarölő szerek használata (kivéve, ha szinte teljesen elpusztítják a rovarokat) végső soron azon rovarok populációjának növekedéséhez vezet, amelyek számát más ragadozó rovarok szabályozzák. Egy Amerikába véletlenül bekerült levéltetű az összes citrustermelést veszélyeztette. Hamarosan odahozták természetes ellenségét. -katicabogár, amely azonnal nekilátott, és nagymértékben csökkentette a levéltetvek számát. A pusztulás folyamatának felgyorsítása érdekében a gazdálkodók DDT-t használtak, de ennek eredményeként megnőtt a levéltetvek száma, ami a rizsre nézve. 2.11 ,nem nehéz megjósolni.
2.3 Mobilizációs modell
A politikai vagy társadalmi mozgósítás kifejezés az emberek bevonását jelenti egy pártba vagy annak támogatói közé, bármilyen társadalmi mozgalomba stb. Mivel a mozgósítás jelenlegi szintje szorosan összefügg a múltbeli szinttel, és a jövőbeni mozgósítás attól függ. A mai sikerek propagandakampányán jól látszik, hogy a megfelelő modell felépítésénél figyelembe kell venni az időfaktort. Más szóval, meg kell értenie, hogy a kívánt modellnek dinamikusnak kell lennie.
A probléma megfogalmazása .Tükrözi azt a logikát, hogy egy adott régióban két szomszédos időpont között, mondjuk egy hónapra (egy évre, egy hétre, egy napra stb.) változik a mozgósítás mértéke.
A modell építése .Vegyük egységnek a lakosságnak azt a részét, amelynél az ilyen típusú mozgósításnak van értelme. Legyen M n -a mobilizált lakosság aránya a t időpontban n = n .Ekkor a nem mozgósított lakosság aránya 1-Mn lesz (2.12. ábra).
Rizs. 2.12. A mobilizált és nem mobilizált lakosság aránya
A mobilizáció mértéke egy hónap alatt változhat két fő okból:
) a lakosság egy része ezen felül vonzotta; jól látható, hogy ez az érték minél nagyobb, annál nagyobb a t időpontban még meg nem ereszkedett populáció aránya n = n ,és ezért egyenrangúnak tekinthető ?(1-M n ),(itt ?>0- kampányolási együttható, egy adott régióra vonatkozóan állandó);
2) a lakosság egy része csökkent (el különböző okok miatt); jól látható, hogy ez minél jobban csökkenti a megnyugvó népesség arányát, minél nagyobb volt ez az arány tn = n időpontban, ezért a nyugdíjba vonuláshoz kapcsolódó veszteségek egyenlőnek tekinthetők (itt?> 0 konstans nyugdíjarány) . Hangsúlyozzuk, hogy a numerikus paraméterek? és? tükrözi a vizsgált régió lakosságának érintett részeinek érdekeinek, nézeteinek és szándékainak arányos változását. Így a mobilizáció mértékének egységnyi idő alatti változása megegyezik a pótlólagosan vonzott népesség és a nyugdíjas nyugalmazott népesség részaránya közötti különbséggel:
Ez a mobilizációs folyamat egyenlete. Kiépült a mobilizációs modell.
Az utolsó arány könnyen átalakítható a következő formára:
Megjegyzés. Kiegészítő paraméter? nem lehet több 1-nél, mivel a kezdeti paraméterek? és? pozitív. Az így kapott (4) egyenletet lineáris differenciaegyenletnek nevezzük állandó együtthatókkal.
Az ilyen egyenletekkel különböző, többnyire a legegyszerűbb változatokban találkozhatunk.
Az egyik (? = 1-re) azt a szabályt írja le, amely szerint a sorozat minden tagja a másodiktól kezdve az előzőből úgy kapható meg, hogy valamilyen állandó számmal összeadjuk: Mn + 1 =? + Mn, azaz egy aritmetriai progresszió.
A második (? = 0 esetén) azt a szabályt írja le, amely szerint a sorozat minden egyes tagját a másodiktól kezdve kapjuk az előzőből valamilyen állandó számmal való szorzással: Mn + 1 =? Mn, azaz egy geometriai progresszió.
Tegyük fel, hogy ismert az M0 vonzott populáció kezdeti részesedése. Ekkor a (4) egyenlet könnyen megoldható (a határozottság kedvéért ezt feltételezzük). Nekünk van:
A modell alkalmazása.
Próbáljuk meg elemezni ennek a (legegyszerűbb szempontok alapján felépített) modellnek a képességeit.
Kezdjük az esettel |? |<1.
Ehhez átírjuk az utolsó arányt az űrlapba, ahol a következő értéket M * jelöli:
Megjegyzés. Ugyanezt az eredményt kapjuk, ha a (4) egyenletbe betesszük Mn + 1 = Mn = M *.
Valóban, akkor azt kapjuk, hogy M * = + + M *, honnan
A talált M * érték nem függ M0 kezdeti értékétől, a kezdeti paraméterekkel van kifejezve? és? képlet szerint
és ezért engedelmeskedik a 0 feltételnek Hogy a kapott képlet leíróbb legyen, ismét a koordináta módszert használjuk. ábrán. A 2.13 a segédparaméter lehetséges értékeinek tartományát mutatja?, az ábrán. 2.14 - kezdeti paraméterek? és?, és az ábrán. 2,15-17 - a különböző n, M0 és M * megfelelő Mn-értékkészletei (az érzékelés megkönnyítése érdekében a szomszédos pontokat (n, Mn) és (n + l, Mn + 1) egyenes szakaszok kötik össze) . Esemény?<1 проиллюстрирован на рис. 2.18. Természetesen ezek a számok jó képet adnak. De semmi sem akadályoz meg bennünket abban, hogy egészen konkrét értékeket vegyünk fel a М0,? és? és számolja ki részletesen a megfelelő helyzetet. Rizs. 2.13 A lehetséges értékek területei? 2.14 Kezdeti paraméterek? és? Rizs. 2,15 - 2,16 Rizs. 2,17 2,18. Esemény?<1 Például nekünk van , ... (2.19. ábra) Rizs. 2.19. Mobilizálás, amikor Érdekes megjegyezni, hogy a felépített modell a megközelítések és az érvelések egyszerűsége ellenére meglehetősen jól tükrözi a valós folyamatokat. Így a javasolt mozgósítási modellt felhasználták a Lake Country (USA) Demokrata Pártra leadott szavazatok számának dinamikájának tanulmányozására 1920-1968 között, és kiderült, hogy elég jól leírja a mozgósítási folyamat minőségi jellemzőit. 2.4 A fegyverkezési verseny modellje Tekintsünk egy konfliktushelyzetet, amelyben két ország kerülhet, az érthetőség kedvéért nevezzük X és Y országoknak. Jelölje x = x (t) X ország élesítésének költségeit, y = y (t) pedig Y ország élesítési költségeit az adott pillanatban. 1. Feltevés. X ország felfegyverkezik, tartva az Y ország esetleges háborús veszélyétől, amely viszont X ország fegyverkezési kiadásainak növekedését ismerve növeli fegyverkezési kiadásait is. Minden ország a másik kiadási szintjével arányosan változtatja a fegyverzet növekedésének (vagy csökkentésének) ütemét. A legegyszerűbb esetben a következőképpen írható le: ahol ?és ?-pozitív állandók. Az írott egyenleteknek azonban van egy nyilvánvaló hátránya - a fegyverek szintjét semmi sem korlátozza. Ezért ezen egyenletek jobb oldalai természetes korrekciót igényelnek. 2. feltételezés. Minél magasabb egy ország védelmi kiadásainak jelenlegi szintje, annál lassabb a növekedési üteme. Ezzel a következő változtatásokat hajthatja végre az előző rendszeren: x = y -? x y = ? x -y ha ez az ország nem fenyegeti ennek a létezését. Jelöljük a megfelelő állításokat a-val és b-vel (a és b pozitív állandók). Ha az a és b állandók negatívak, akkor ezeket goodwill együtthatónak nevezhetjük. Mindhárom feltételezés alapján az eredmény a következő egyenletrendszer: x = y- x + a y = X - y + b Megépült a fegyverkezési versenymodell. A kapott rendszer megoldása az x (t) és y (t) függvény, amelyet az adott x kezdeti feltételekre határozunk meg. 00 és y 0? 0 (a fegyverkezési verseny kezdeti állapota). Elemezzük az így létrejött rendszert, feltételezve, hogy mindkét ország fegyverkiadásainak mértéke nem időfüggő (helyhez kötött). Ez azt jelenti, hogy x = 0, y = 0 vagy más: Y- ? x + a = 0 X- y + b = 0 Nézzünk egy konkrét példát. Példa. Legyen a fegyverkezési verseny rendszere a következő: x = 3y-5x + 15 y = 3x-4y + 12 Ha az x és y mennyiségek változási sebessége nulla, akkor ezek a mennyiségek szükségszerűen összefüggenek a feltételekkel: Mindegyik egyenlet egy egyenest ír le a síkban (x, y), és ezen egyenesek metszéspontja az első negyedben van (2.20. ábra). Az (a) egyenlet által adott egyenes felosztja a síkot, és az O (0,0) kezdőpont a pozitív félsíkban található. A vizsgált esetben ugyanez igaz a (b) egyenlet által adott egyenesre is (2.21. ábra). Így az első negyed (és minket csak ez érdekel, hiszen mindig x? 0 és y? 0) négy régióra oszlik, amelyeket kényelmesen a következőképpen jelölünk: I - (+, +), II - (-, +), III- (-, -), IV - (+, -). Legyen a kezdeti állapot (x 0, nál nél 0) az I. tartományban van. Ekkor a következő egyenlőtlenségek teljesülnek: (a): 3y0 -5x 0+15>0,
(b): 3x 0-4 év 0+12>0,
amiből az következik, hogy az x "és y" sebességek ezen a ponton pozitívak: x "> 0, y"> 0, és ezért mindkét mennyiségnek (x és y) növekednie kell (2.22. ábra). Rizs. 2.22 .x és y növelése Így az I. tartományban az idő múlásával a megoldás egyensúlyi ponthoz jut. Hasonló módon, elemezve a kezdeti állapot lehetséges helyeit a II., III. és IV. régióban, azt találjuk, hogy a stabil állapot (erőegyensúly) az X és Y országok kezdeti fegyverszintjétől függetlenül elérhető. Az egyetlen különbség az, hogy ha az I. területről a stacionárius állapotba való átmenet a fegyverzetszint egyidejű növekedésével jár, akkor a III. -egyidejű csökkenésük; a II. és IV. régió esetében más a helyzet -az egyik oldal felfegyverzi, míg a másik lefegyverzi. Más esetek is lehetségesek (2.23. ábra). Rizs. 2.23 ... egyéb esetek Érdekes megjegyezni, hogy az elkészített modell képességeit valós helyzetben tesztelték. -az első világháború előtti fegyverkezési verseny. Tanulmányok kimutatták, hogy egyszerűsége ellenére ez a modell meglehetősen megbízhatóan írja le az 1909-1913 közötti európai állapotokat. A fejezet zárásaként idézzük T. Saaty kijelentését a modellről: „A modell sokkal meggyőzőbbnek tűnik, ha a fegyverek helyett a fenyegetés problémáinak tanulmányozására használják, mivel az emberek az ellenséges ellenségesség abszolút szintjére reagálnak. mások által velük szemben, és megtapasztalják az általuk érzett ellenségeskedés mértékével arányos érzést." Következtetés Napjainkban a tudomány egyre nagyobb figyelmet szentel a szervezés és irányítás kérdéseinek, ez megköveteli az összetett, célirányos folyamatok felépítésük, szervezettségük szempontjából történő elemzését. A praxis igénye sajátos módszereket eredményezett, amelyek kényelmesen kombinálhatók „operációkutatás” néven. Ez a kifejezés a matematikai, kvantitatív módszerek alkalmazását jelenti a döntések igazolására a céltudatos emberi tevékenység minden területén. Az operációkutatás célja egy adott probléma megoldásában a legjobb cselekvési mód azonosítása. Ebben a főszerep a matematikai modellezésé. A matematikai modell felépítéséhez szigorúan ismerni kell a vizsgált rendszer működésének célját, és rendelkezni kell azokról a korlátokról, amelyek a megengedett értékek tartományát meghatározzák. A célt és a korlátokat függvények formájában kell bemutatni. Az operációkutatási modellekben azok a változók, amelyektől a megszorítások és a célfüggvény függnek, lehetnek diszkrét (leggyakrabban egész) és folytonos (folyamatos). A megszorításokat és a célfüggvényt viszont lineárisra és nemlineárisra osztják. E modellek megoldására többféle módszer létezik, ezek közül a leghíresebb és leghatékonyabbak a lineáris programozási módszerek, amikor a célfüggvény és az összes megszorítás lineáris. Más típusú matematikai modellek megoldására szolgálnak a dinamikus programozás módszerei (amelyeket ebben a kurzusban tárgyaltunk), az egészszámú programozás, a nemlineáris programozás, a többcélú optimalizálás és a hálózati modellek módszerei. Szinte minden műveletkutatási módszer iteratív jellegű számítási algoritmusokat generál. Ez azt jelenti, hogy a probléma szekvenciálisan (iteratívan) megoldódik, amikor minden lépésben (iteráció) kapunk egy olyan megoldást, amely fokozatosan konvergál az optimális megoldáshoz. Az algoritmusok iteratív jellege általában azonos típusú, terjedelmes számításokhoz vezet. Ez az oka annak, hogy ezeket az algoritmusokat elsősorban számítógépes megvalósításra fejlesztették ki. A modell felépítése a vizsgált helyzet jelentős egyszerűsítésén és ,ezért az alapján levont következtetéseket kellő óvatossággal kell kezelni. -a modell nem tud mindent. Ugyanakkor a látszólag nagyon durva idealizálás is gyakran lehetővé teszi a probléma lényegének mélyebbre ásását. Megpróbálva valamilyen módon befolyásolni a modell paramétereit (kiválasztani, ellenőrizni), lehetőséget kapunk arra, hogy a vizsgált jelenséget kvalitatív elemzésnek vessük alá, és általános következtetéseket vonjunk le. A dinamikus programozás egy matematikai berendezés, amely lehetővé teszi a többlépéses időfüggő folyamatok optimális tervezését. Mivel a dinamikus programozási problémákban a folyamatok időfüggőek, minden szakaszra számos optimális megoldás születik, amelyek biztosítják a teljes folyamat egészének optimális fejlődését. A fázisos tervezéssel a dinamikus programozás nemcsak a problémák megoldásának egyszerűsítését teszi lehetővé, hanem olyan problémák megoldását is, amelyekre a matematikai elemzés módszerei nem alkalmazhatók. Biztosan ,nem ér semmit ,hogy ez a módszer meglehetősen időigényes a nagyszámú változót tartalmazó problémák megoldása során. Bibliográfia 1.Akulich I.L. Matematikai programozás példákban és feladatokban: Tankönyv. kézikönyv. - M .: Felsőiskola, 2009 .Berezhnaya E.V., Berezhnoy V.I. Matematikai modellezési módszerek. - M .: Delo és szerviz, 2009 .Intriligátor M. Az optimalizálás matematikai módszerei és a közgazdaságtan. - M .: Iris-Press, 2008 .Kurbatov V.I., Ugolnitsky G.A. A szociális technológiák matematikai módszerei. - M .: Egyetemi könyv, 2011 .A. V. Monakhov A közgazdasági elemzés matematikai módszerei. - SPb .: Péter, 2007 .Orlova I.V., Polovnikov V.A. Gazdasági és matematikai módszerek és modellek. - M .: Egyetemi tankönyv, 2008 .Popov I.I., Partyka T.L. Matematikai módszerek. - M .: INFRA-M, 2007 .Popova N.V. Matematikai módszerek. - M .: Ankil, 2007 Segítségre van szüksége egy téma feltárásához?
Szakértőink tanácsot adnak vagy oktatói szolgáltatásokat nyújtanak az Önt érdeklő témákban.
Korrepetálás
Kérelmet küldeni a téma megjelölésével már most tájékozódni a konzultáció lehetőségéről.
X360ce - bármilyen joystick csatlakoztatása (útmutató a régi verzióhoz) Telepítse a joystickot a számítógépére Xbox 360-ról
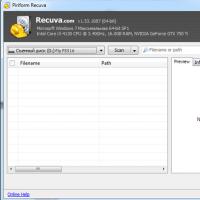Névjegyek helyreállítása Androidon
Pizza Birodalom promóciós kódja október
Miért nem csatlakozik a kormánykerék a számítógéphez?
Hogyan lehet játékkereket csatlakoztatni a számítógéphez
Hogyan kell személyes naplót vezetni és mi a haszna
"Cedar" töltő: leírás, használati utasítás