Produkt matice podľa čísla online. Základné operácie s maticami (sčítanie, násobenie, transpozícia) a ich vlastnosti. Vlastnosti násobenia matice číslom
Táto téma sa bude zaoberať takými operáciami, ako je sčítanie a odčítanie matíc, násobenie matice číslom, násobenie matice maticou a transpozícia matice. Všetky symboly použité na tejto stránke sú prevzaté z predchádzajúcej témy.
Sčítanie a odčítanie matíc.
Súčet $ A + B $ matíc $ A_ (m \ times n) = (a_ (ij)) $ a $ B_ (m \ times n) = (b_ (ij)) $ sa nazýva matica $ C_ (m \ times n) = (c_ (ij)) $, kde $ c_ (ij) = a_ (ij) + b_ (ij) $ pre všetky $ i = \ overline (1, m) $ a $ j = \ overline ( 1, n) $.
Podobná definícia je zavedená aj pre rozdiel matíc:
Rozdiel $ AB $ matíc $ A_ (m \ times n) = (a_ (ij)) $ a $ B_ (m \ times n) = (b_ (ij)) $ je matica $ C_ (m \ times n ) = (c_ (ij)) $, kde $ c_ (ij) = a_ (ij) -b_ (ij) $ pre všetky $ i = \ overline (1, m) $ a $ j = \ overline (1, n ) $.
Vysvetlenie položky $ i = \ overline (1, m) $: show \ hide
Zápis „$ i = \ overline (1, m) $“ znamená, že parameter $ i $ sa pohybuje od 1 do m. Záznam $ i = \ overline (1,5) $ napríklad hovorí, že parameter $ i $ má hodnoty 1, 2, 3, 4, 5.
Je potrebné poznamenať, že operácie sčítania a odčítania sú definované iba pre matice rovnakej veľkosti. Sčítanie a odčítanie matíc sú vo všeobecnosti intuitívne jasné operácie, pretože v skutočnosti znamenajú iba sčítanie alebo odčítanie zodpovedajúcich prvkov.
Príklad č. 1
Sú uvedené tri matice:
$$ A = \ left (\ begin (array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (array) \ right) \; \; B = \ left (\ begin (array) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (array) \ right); \; \; F = \ left (\ begin (array) (cc) 1 & 0 \\ -5 & 4 \ end (array) \ right). $$
Nájdete maticu $ A + F $? Nájdite matice $ C $ a $ D $, ak $ C = A + B $ a $ D = A-B $.
Matica $ A $ obsahuje 2 riadky a 3 stĺpce (inými slovami, veľkosť matice $ A $ je $ 2 \ krát 3 $) a matica $ F $ obsahuje 2 riadky a 2 stĺpce. Veľkosti matice $ A $ a $ F $ sa nezhodujú, preto ich nemôžeme sčítať, t.j. operácia $ A + F $ pre tieto matice nie je definovaná.
Veľkosti matíc $ A $ a $ B $ sú rovnaké, t.j. maticové údaje obsahujú rovnaký počet riadkov a stĺpcov, takže sa na ne dá použiť operácia sčítania.
$$ C = A + B = \ vľavo (\ begin (pole) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (pole) \ right) + \ left (\ begin (pole ) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (array) \ right) = \\ = \ left (\ begin (array) (ccc) -1 + 10 & -2+ ( -25) & 1 + 98 \\ 5 + 3 & 9 + 0 & -8 + ( -14) \ end (pole) \ right) = \ left (\ begin (array) (ccc) 9 & -27 & 99 \\ 8 a 9 & -22 \ end (pole) \ vpravo) $$
Nájdite maticu $ D = A-B $:
$$ D = AB = \ left (\ begin (array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (array) \ right) -\ left (\ begin (array) ( ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (array) \ right) = \\ = \ left (\ begin (array) (ccc) -1-10 & -2 -( -25 ) & 1-98 \\ 5-3 & 9-0 & -8 -( -14) \ end (pole) \ right) = \ left (\ begin (array) (ccc) -11 & 23 & -97 \ \ 2 a 9 a 6 \ koniec (pole) \ vpravo) $$
Odpoveď: $ C = \ left (\ begin (array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \ end (array) \ right) $, $ D = \ left (\ begin (array) (ccc) -11 & 23 & -97 \\ 2 & 9 & 6 \ end (array) \ right) $.
Násobenie matice číslom.
Súčet matice $ A_ (m \ times n) = (a_ (ij)) $ podľa čísla $ \ alpha $ je matica $ B_ (m \ krát n) = (b_ (ij)) $, kde $ b_ (ij) = \ alpha \ cdot a_ (ij) $ pre všetky $ i = \ overline (1, m) $ a $ j = \ overline (1, n) $.
Jednoducho povedané, vynásobenie matice určitým číslom znamená vynásobenie každého prvku danej matice týmto číslom.
Príklad č. 2
Matica je daná: $ A = \ left (\ begin (array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (array) \ right) $. Nájdite matice $ 3 \ cdot A $, $ -5 \ cdot A $ a $ -A $.
$$ 3 \ cdot A = 3 \ cdot \ left (\ begin (array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (array) \ right) = \ left (\ begin ( pole) (ccc) 3 \ cdot (-1) & 3 \ cdot (-2) & 3 \ cdot 7 \\ 3 \ cdot 4 & 3 \ cdot 9 & 3 \ cdot 0 \ end (array) \ right) = \ left (\ begin (array) (ccc) -3 & -6 & 21 \\ 12 & 27 & 0 \ end (array) \ right). \\ -5 \ cdot A = -5 \ cdot \ left (\ begin (array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (array) \ right) = \ left (\ begin (array) (ccc) -5 \ cdot (-1) & -5 \ cdot (-2) & -5 \ cdot 7 \\ -5 \ cdot 4 & -5 \ cdot 9 & -5 \ cdot 0 \ end (pole) \ right) = \ left (\ begin (array) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \ end (pole) \ right). $$
Zápis $ -A $ je skratkou pre $ -1 \ cdot A $. To znamená, že na nájdenie $ -A $ je potrebné vynásobiť všetky prvky matice $ A $ číslom (-1). V skutočnosti to znamená, že znamienko všetkých prvkov matice $ A $ sa zmení na opak:
$$ -A = -1 \ cdot A = -1 \ cdot \ left (\ begin (array) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (array) \ right) = \ vľavo (\ begin (pole) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \ end (pole) \ right) $$
Odpoveď: $ 3 \ cdot A = \ left (\ begin (array) (ccc) -3 & -6 & 21 \\ 12 & 27 & 0 \ end (array) \ right); \; -5 \ cdot A = \ vľavo (\ begin (pole) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \ end (pole) \ right); \; -A = \ left (\ begin (array) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \ end (array) \ right) $.
Súčin dvoch matríc.
Definícia tejto operácie je ťažkopádna a na prvý pohľad nepochopiteľná. Preto najskôr uvediem všeobecnú definíciu a potom podrobne analyzujeme, čo to znamená a ako s tým pracovať.
Matica $ C_ (m \ krát k) = (c_ (ij)) $, pre ktorú je každý prvok $ c_ (ij) $ rovný súčtu súčinov zodpovedajúcich prvkov i-tého riadka matica $ A $ prvkami j-tého stĺpca matice $ B $: $$ c_ (ij) = \ sum \ limits_ (p = 1) ^ (n) a_ (ip) b_ (pj), \ ; \; i = \ overline (1, m), j = \ overline (1, n). $$
Poďme analyzovať multiplikáciu matice krok za krokom na príklade. Mali by ste však okamžite venovať pozornosť skutočnosti, že nie všetky matrice je možné vynásobiť. Ak chceme vynásobiť maticu $ A $ maticou $ B $, musíme sa najskôr uistiť, že počet stĺpcov matice $ A $ je rovný počtu riadkov matice $ B $ (takéto matice sa často nazývajú súhlasil). Napríklad maticu $ A_ (5 \ krát 4) $ (matica obsahuje 5 riadkov a 4 stĺpce) nemožno vynásobiť maticou $ F_ (9 \ krát 8) $ (9 riadkov a 8 stĺpcov), pretože číslo stĺpcov matice $ A $ sa nerovná počtu riadkov v matici $ F $, t.j. 4 doláre \ neq 9 $. Maticu $ A_ (5 \ krát 4) $ však môžete vynásobiť maticou $ B_ (4 \ krát 9) $, pretože počet stĺpcov v matici $ A $ sa rovná počtu riadkov v matici $ B $. V tomto prípade bude výsledkom vynásobenia matíc $ A_ (5 \ krát 4) $ a $ B_ (4 \ krát 9) $ matica $ C_ (5 \ krát 9) $, obsahujúca 5 riadkov a 9 stĺpcov:
Príklad č. 3
Matice sú dané: $ A = \ left (\ begin (array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \ end (array) \ right) $ and $ B = \ left (\ begin (array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \ end (array) \ right ) $. Nájdite maticu $ C = A \ cdot B $.
Na začiatok hneď určíme veľkosť matice $ C $. Pretože $ A $ je $ 3 \ krát 4 $ a $ B $ je $ 4 \ krát 2 $, veľkosť $ C $ je $ 3 \ krát 2 $:

Výsledkom súčinu matíc $ A $ a $ B $ by mala byť matica $ C $ pozostávajúca z troch riadkov a dvoch stĺpcov: $ C = \ left (\ begin (pole) (cc) c_ (11) & c_ (12) \\ c_ (21) & c_ (22) \\ c_ (31) & c_ (32) \ end (pole) \ vpravo) $. Ak označenie prvkov vyvoláva otázky, môžete sa pozrieť na predchádzajúcu tému: „Matice. Typy matíc. Základné pojmy“, na začiatku ktorých je vysvetlené označenie prvkov matice. Našim cieľom je nájsť hodnoty všetkých prvkov matice $ C $.
Začnime s $ c_ (11) $. Ak chcete získať prvok $ c_ (11) $, musíte nájsť súčet súčinov prvkov prvého riadka matice $ A $ a prvého stĺpca matice $ B $:

Aby ste našli samotný prvok $ c_ (11) $, musíte vynásobiť prvky prvého riadka matice $ A $ zodpovedajúcimi prvkami prvého stĺpca matice $ B $, t.j. prvý prvok k prvému, druhý k druhému, tretí k tretiemu, štvrtý k štvrtému. Sumarizujeme získané výsledky:
$$ c_ (11) =- 1 \ cdot (-9) +2 \ cdot 6 + (- 3) \ cdot 7 + 0 \ cdot 12 = 0. $$
Pokračujme v riešení a nájdeme $ c_ (12) $. Aby ste to urobili, musíte vynásobiť prvky prvého riadka matice $ A $ a druhého stĺpca matice $ B $:

Podobne ako v predchádzajúcom prípade máme:
$$ c_ (12) =- 1 \ cdot 3 + 2 \ cdot 20 + (- 3) \ cdot 0 + 0 \ cdot (-4) = 37. $$
Nachádzajú sa všetky prvky prvého riadka $ C $. Prejdite na druhý riadok, ktorý začína na $ c_ (21) $. Aby ste to našli, musíte vynásobiť prvky druhého riadka matice $ A $ a prvého stĺpca matice $ B $:

$$ c_ (21) = 5 \ cdot (-9) +4 \ cdot 6 + (-2) \ cdot 7 + 1 \ cdot 12 = -23. $$
Ďalší prvok $ c_ (22) $ sa nájde vynásobením prvkov druhého riadka matice $ A $ zodpovedajúcimi prvkami druhého stĺpca matice $ B $:
$$ c_ (22) = 5 \ cdot 3 + 4 \ cdot 20 + (- 2) \ cdot 0 + 1 \ cdot (-4) = 91. $$
Aby sme našli $ c_ (31) $, vynásobíme prvky tretieho riadka matice $ A $ prvkami prvého stĺpca matice $ B $:
$$ c_ (31) =- 8 \ cdot (-9) +11 \ cdot 6 + (- 10) \ cdot 7 + (-5) \ cdot 12 = 8. $$
A nakoniec, aby ste našli prvok $ c_ (32) $, musíte prvky tretieho riadka matice $ A $ vynásobiť zodpovedajúcimi prvkami druhého stĺpca matice $ B $:
$$ c_ (32) =- 8 \ cdot 3 + 11 \ cdot 20 + (- 10) \ cdot 0 + (-5) \ cdot (-4) = 216. $$
Sú nájdené všetky prvky matice $ C $, zostáva len napísať, že $ C = \ left (\ begin (pole) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (pole ) \ vpravo) $ ... Alebo napísať úplne:
$$ C = A \ cdot B = \ vľavo (\ begin (pole) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & - 5 \ end (pole) \ right) \ cdot \ left (\ begin (array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \ end (array) \ right) = \ left (\ begin (array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (array) \ right). $$
Odpoveď: $ C = \ left (\ begin (array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (array) \ right) $.
Mimochodom, často neexistuje dôvod podrobne popisovať zistenie každého prvku matice výsledkov. V prípade matríc, ktorých veľkosť je malá, môžete urobiť nasledovné:
$$ \ left (\ begin (array) (cc) 6 & 3 \\ -17 & -2 \ end (array) \ right) \ cdot \ left (\ begin (array) (cc) 4 & 9 \\ - 6 & 90 \ end (pole) \ right) = \ left (\ begin (array) (cc) 6 \ cdot (4) +3 \ cdot (-6) & 6 \ cdot (9) +3 \ cdot (90 ) \\ -17 \ cdot (4) + (-2) \ cdot (-6) & -17 \ cdot (9) + (-2) \ cdot (90) \ end (array) \ right) = \ left (\ begin (pole) (cc) 6 & 324 \\ -56 & -333 \ end (pole) \ right) $$
Je tiež potrebné poznamenať, že násobenie matice nie je komutatívne. To znamená, že vo všeobecnosti $ A \ cdot B \ neq B \ cdot A $. Iba pre niektoré typy matíc, ktoré sa nazývajú permutácia(alebo dochádzanie za prácou), rovnosť $ A \ cdot B = B \ cdot A $ je pravdivá. Práve na základe nekomutativity násobenia je potrebné presne naznačiť, ako výraz vynásobíme tou alebo onou maticou: vpravo alebo vľavo. Napríklad fráza „vynásobte obe strany rovnosti $ 3E-F = Y $ maticou $ A $ vpravo“ znamená, že potrebujeme získať nasledujúcu rovnosť: $ (3E-F) \ cdot A = Y \ cdot A $.
Transponované vzhľadom na maticu $ A_ (m \ times n) = (a_ (ij)) $ sa nazýva matica $ A_ (n \ times m) ^ (T) = (a_ (ij) ^ (T)) $ , pre prvky, ktoré $ a_ (ij) ^ (T) = a_ (ji) $.
Jednoducho povedané, aby ste získali transponovanú maticu $ A ^ T $, musíte nahradiť stĺpce v pôvodnej matici $ A $ zodpovedajúcimi riadkami podľa nasledujúceho princípu: ak bol prvý riadok, prvý stĺpec sa stane ; bol tu druhý riadok - bude druhý stĺpec; bol tam tretí riadok - bude tam tretí stĺpec a tak ďalej. Nájdeme napríklad transponovanú maticu na maticu $ A_ (3 \ krát 5) $:

V súlade s tým, ak pôvodná matica bola 3 doláre \ krát 5 dolárov, potom transponovaná matica je 5 dolárov \ krát 3 doláre.
Niektoré vlastnosti operácií s maticami.
Tu sa predpokladá, že $ \ alpha $, $ \ beta $ sú niektoré čísla a $ A $, $ B $, $ C $ sú matice. Pre prvé štyri vlastnosti som uviedol názvy, ostatné je možné pomenovať analogicky s prvými štyrmi vlastnosťami.
Prednáška číslo 1
MATRIX
Definícia a typy matíc
Definícia 1.1.Matica veľkosť T NS nazývaná obdĺžniková tabuľka čísel (alebo iných predmetov) obsahujúca m linky a n stĺpce.
Matice sú označené veľkými (veľkými) písmenami latinskej abecedy, napríklad A, B, C, ... Nazývajú sa čísla (alebo iné objekty), ktoré tvoria maticu prvky matrice. Prvkami matice môžu byť funkcie. Na označenie prvkov matice sa používajú malé písmená latinskej abecedy s dvojitým indexovaním: ahoj, kde prvý index i(čítanie - a) - číslo riadku, druhý index j(čítaj - zhi) – číslo stĺpca.
Definícia 1.2. Matica sa nazýva štvorec n- poradie, ak sa počet jeho riadkov rovná počtu stĺpcov a rovná sa rovnakému číslu NS
Pre štvorcovú maticu sú zavedené koncepty hlavné a vedľajšie uhlopriečky.
Definícia 1.3.Hlavná uhlopriečkaštvorcová matica pozostáva z prvkov s rovnakými indexmi, t.j. Toto sú prvky: a 11, 22, ...
Definícia 1.4. uhlopriečka ak sú všetky prvky, okrem prvkov hlavnej uhlopriečky, rovné nule
Definícia 1.5.Štvorcová matica sa nazýva trojuholníkový ak sú všetky jeho prvky umiestnené pod (alebo nad) hlavnou uhlopriečkou rovné nule.
Definícia 1.6.Štvorcová matica NS- ten poriadok, v ktorom sú všetky prvky hlavnej uhlopriečky rovné jednej a ostatné sú rovné nule, sa nazýva slobodný matica n-th order, a je označený písmenom E.
Definícia 1.7. Nazýva sa matica akejkoľvek veľkosti nulový, alebo nulová matica, ak sú všetky jeho prvky rovné nule.
Definícia 1.8. Nazýva sa jednoradová matica maticový riadok.
Definícia 1.9. Nazýva sa matica jedného stĺpca stĺpcová matica.
A = (a 11 a 12 ... a 1n) - riadková matica;
Definícia 1.10. Dve matice A a V. nazývajú sa rovnako veľké rovný, ak sú všetky zodpovedajúce prvky týchto matíc navzájom rovnaké, t.j. aij = bij pre hocikoho i= 1, 2, ..., T; j = 1, 2,…, n.
Maticové operácie
Niekoľko operácií je možné vykonať s maticami, ako aj s číslami. Hlavnými operáciami s maticami sú sčítanie (odčítanie) matíc, násobenie matice číslom a násobenie matice. Tieto operácie sú podobné operáciám s číslami. Špecifickou operáciou je transpozícia matice.
Vynásobenie matice číslom
Definícia 1.11.Súčin matice A podľa číslaλ sa nazýva matica B = A, ktorých prvky sa získavajú vynásobením prvkov matice Ačíslom λ .
Príklad 1.1. Nájdite súčin matice A = ![]() na číslo 5.
na číslo 5.
Riešenie... .◄ 5A = ![]()
Pravidlo násobenia matice číslom: na vynásobenie matice číslom musia byť všetky prvky matice vynásobené týmto číslom.
Dôsledok.
1. Spoločný faktor všetkých prvkov matice je možné vylúčiť zo znaku matice.
2. Súčin matice A pre číslo 0 existuje nulová matica: A· 0 = 0 .
Pridanie matice
Definícia 1.12.Súčet dvoch matíc A a B rovnakú veľkosť t n nazýva sa matica S= A+ V., ktorých prvky sa získajú sčítaním zodpovedajúcich prvkov matice A a matrice V., t.j. cij = aij + bij pre i = 1, 2, ..., m; j= 1, 2, ..., n(t.j. matice sa pridávajú prvok po prvku).
Dôsledok. Maticová suma A s nulovou maticou sa rovná pôvodnej matici: A + O = A.
1.2.3. Odčítanie matíc
Rozdiel dvoch matíc rovnaká veľkosť sa určuje pomocou predchádzajúcich operácií: A - B = A + ( - 1) V.
Definícia 1.13. Matica –A = (- 1) A zavolal opak matica A.
Dôsledok. Súčet opačných matíc sa rovná nulovej matici : A + (–A) = O.
Maticové násobenie
Definícia 1.14.Násobenie matice A maticou B určuje sa, keď sa počet stĺpcov prvej matice rovná počtu riadkov druhej matice. Potom výrobok z matríc taká matica sa nazýva , z ktorých každý prvok cij sa rovná súčtu súčinov prvkov i-tretí riadok matice A na zodpovedajúcich prvkoch j stĺpec matice B.
Príklad 1.4. Vypočítajte súčin matíc А В, kde
A = 
= ![]()
Príklad 1.5. Nájdite maticové produkty AB a VA, kde
Poznámky. Z príkladov 1.4 - 1.5 vyplýva, že prevádzka násobenia matíc má určité rozdiely od násobenia čísel:
1) ak je súčin matríc AB existuje, potom po preskupení faktorov na miestach vznikne súčin matíc VA nemusí existovať. V Príklade 1.4 skutočne existuje produkt matíc AB, ale produkt BA neexistuje;
2) aj keď to funguje AB a VA existujú, potom výsledkom produktu môžu byť matice rôznych veľkostí. V prípade, že fungujú obe AB a VA obidve existujú - matice rovnakej veľkosti (je to možné iba pri vynásobení štvorcových matíc rovnakého poradia), potom komutatívny (transponovateľný) zákon násobenia stále neplatí, tí. A B B A, ako v príklade 1.5;
3) ak však vynásobíme štvorcovú maticu A na matici identity E teda rovnakého poriadku AE = EA = A.
Matica identity pri násobení matice teda hrá rovnakú úlohu ako číslo 1 pri násobení čísel;
4) súčin dvoch nenulových matíc sa môže rovnať nulovej matici, to znamená zo skutočnosti, že A B= 0, z toho nevyplýva A = 0 alebo B = 0.
1. ročník, vyššia matematika, študujeme matrice a základné akcie na nich. Tu systematizujeme základné operácie, ktoré je možné vykonávať s maticami. Kde začať zoznamovanie s maticami? Samozrejme, od tých najjednoduchších - definícií, základných pojmov a najjednoduchších operácií. Uisťujeme vás, že matici porozumie každý, kto sa im aspoň trochu venuje!
Definícia matice
Matica Je to obdĺžniková tabuľka prvkov. Ak je to zjednodušene povedané - tabuľka čísel.
Matice sú zvyčajne označené veľkými latinskými písmenami. Napríklad matica A , matica B atď. Matice môžu mať rôzne veľkosti: obdĺžnikové, štvorcové, existujú aj riadkové matice a stĺpcové matice, nazývané vektory. Veľkosť matice je určená počtom riadkov a stĺpcov. Napíšte napríklad obdĺžnikovú maticu veľkosti m na n , kde m - počet riadkov a n - počet stĺpcov.

Prvky, pre ktoré i = j (a11, a22, .. ) tvoria hlavnú uhlopriečku matice a nazývajú sa uhlopriečka.
Čo môžete robiť s maticami? Sčítať / odčítať, vynásobte číslom, množiť sa medzi sebou, transponovať... Teraz o všetkých týchto základných operáciách s maticami v poriadku.
Operácie sčítania a odčítania matice
Hneď vás upozorňujeme, že môžete pridať iba matice rovnakej veľkosti. Výsledkom je matica rovnakej veľkosti. Sčítanie (alebo odčítanie) matíc je jednoduché - stačí pridať ich príslušné prvky ... Uveďme príklad. Pridajme dve matice A a B vo veľkosti dva po dvoch.

Odčítanie sa vykonáva analogicky, iba s opačným znamienkom.
Akákoľvek matica môže byť vynásobená ľubovoľným číslom. Robiť to, musíte vynásobiť každý z jeho prvkov týmto číslom. Vynásobme napríklad maticu A z prvého príkladu číslom 5:

Operácia násobenia matice
Nie všetky matrice je možné medzi sebou znásobiť. Máme napríklad dve matice - A a B. Môžu sa navzájom vynásobiť, iba ak je počet stĺpcov matice A rovný počtu riadkov matice B. V tomto prípade každý prvok výslednej matice, stojaci v i-tom riadku a j-tom stĺpci, sa bude rovnať súčtu súčinov zodpovedajúcich prvkov v i-tom riadku prvého faktora a j-týho stĺpca druhy... Aby sme pochopili tento algoritmus, napíšeme si, ako sa vynásobia dve štvorcové matice:

A príklad so skutočnými číslami. Vynásobme matice:

Operácia transpozície matice
Maticová transpozícia je operácia, pri ktorej sa vymieňajú zodpovedajúce riadky a stĺpce. Transponujme napríklad maticu A z prvého príkladu:

Determinant matice
Determinant, ale determinant je jedným zo základných pojmov lineárnej algebry. Ľudia kedysi vymysleli lineárne rovnice a za nimi museli vymyslieť determinant. Výsledkom je, že sa s tým všetkým musíte vyrovnať, takže, posledný špurt!
Determinant je numerická charakteristika štvorcovej matice, ktorá je potrebná na vyriešenie mnohých problémov.
Na výpočet determinantu najjednoduchšej štvorcovej matice je potrebné vypočítať rozdiel medzi produktmi prvkov hlavnej a sekundárnej uhlopriečky.
Determinant matice prvého rádu, to znamená, že pozostáva z jedného prvku, sa rovná tomuto prvku.
Čo keď je matica tri krát tri? Tu je to už zložitejšie, ale dá sa to zvládnuť.
Pre takú maticu je hodnota determinantu rovná súčtu súčinov prvkov hlavnej uhlopriečky a súčinov prvkov ležiacich na trojuholníkoch s tvárou rovnobežnou s hlavnou uhlopriečkou, z ktorej je súčin súčiniteľa prvky bočnej uhlopriečky a súčin prvkov ležiacich na trojuholníkoch s tvárou rovnobežnej bočnej uhlopriečky sa odpočítajú.
Našťastie je v praxi len zriedka potrebné vypočítať determinanty veľkých matíc.
Tu sme pokryli základné operácie s maticami. Samozrejme, v reálnom živote sa nikdy nemôžete stretnúť ani s náznakom maticového systému rovníc, alebo naopak - čeliť oveľa ťažším prípadom, keď si musíte poriadne zlomiť hlavu. Práve pre takéto prípady existuje profesionálna služba pre študentov. Požiadajte o pomoc, získajte vysokokvalitné a podrobné riešenie, užite si akademický úspech a voľný čas.
Na vynásobenie matice A ľubovoľným číslom α potrebujete prvky matice A vynásobte číslom α, t.j. súčin matice s číslom bude nasledujúci:

Príklad 1. Nájdi maticu 3 A pre maticu

Riešenie. V súlade s definíciou vynásobíme prvky matice A o 3 a dostaneme

Bol to veľmi jednoduchý príklad vynásobenia matice číslom s celými číslami. Vpredu sú aj jednoduché príklady, ale už také, kde medzi faktormi a prvkami matíc sú zlomky, premenné (označenia písmen), pretože zákony násobenia platia nielen pre celé čísla, takže nie je nikdy na škodu ich zopakovať.
Príklad 2. Ačíslom α ak  ,
.
,
.
Aα, pričom nezabúdame, že pri násobení zlomkov sa čitateľ prvého zlomku vynásobí čitateľom prvého zlomku a produkt sa zapíše do čitateľa a menovateľ prvého zlomku sa vynásobí menovateľom druhého zlomku a výrobok je zapísaný v menovateli. Pri prijatí druhého prvku prvého radu novej matice sa výsledná frakcia znížila o 2, to sa musí urobiť. Dostaneme

Príklad 3. Vykonajte operáciu násobenia matice Ačíslom α ak
,
.
Riešenie. Vynásobte prvky matice A pomocou α, bez toho, aby ste sa pomýlili v zápise písmen, nezabudnite nechať mínus pred druhým prvkom druhého riadku novej matice a pamätajte na to, že výsledok vynásobenia čísla jeho inverzným číslom je jedna (prvá prvok tretieho radu). Dostaneme
 .
.
Príklad 4. Vykonajte operáciu násobenia matice Ačíslom α ak  ,
.
,
.
Riešenie. Pamätajte si, že keď vynásobíte číslo v mocnine číslom v moci, pripočítajú sa exponenty. Dostaneme
 .
.
Tento príklad, okrem iného, jasne ukazuje, že operácie vynásobenia matice číslom je možné čítať (a zapisovať) v opačnom poradí a nazýva sa to kladenie konštantného faktora pred maticu.
Skombinované s sčítanie a odčítanie matíc operácia násobenia matice číslom môže vytvárať rôzne maticové výrazy, napríklad 5 A − 3B , 4A + 2B .
Vlastnosti násobenia matice číslom
(tu A, B - matice, - čísla, 1 - číslo jedna)
1. ![]()
2. ![]()
3. ![]()
Vlastnosti (1) a (2) spájajú násobenie matice číslom s pridaním matíc. Existuje tiež veľmi dôležité spojenie medzi vynásobením matice číslom a vynásobením samotných matíc:
to znamená, že ak je v súbore matíc vynásobený jeden z faktorov číslom, potom sa celý produkt vynásobí číslom.
Táto metodická príručka vám pomôže naučiť sa vykonávať operácie s maticami: sčítanie (odčítanie) matíc, transpozícia matice, násobenie matíc, hľadanie inverznej matice. Všetok materiál je prezentovaný jednoduchou a prístupnou formou, sú uvedené relevantné príklady, takže aj nepripravený človek sa môže naučiť vykonávať akcie pomocou matíc. Pre samokontrolu a samokontrolu si môžete zadarmo stiahnuť maticovú kalkulačku >>>.
Pokúsim sa minimalizovať teoretické výpočty, na niektorých miestach sú možné vysvetlenia „na prstoch“ a používanie nevedeckých výrazov. Milovníci solídnej teórie, prosím, nekritizujte, našou úlohou je naučte sa vykonávať akcie pomocou matíc.
Na SUPER-RÝCHLU prípravu na tému (kto „horí“) slúži intenzívny kurz pdf Matica, determinant a test!
Matrix je obdĺžniková tabuľka ľubovoľných prvky... Ako prvky budeme brať do úvahy čísla, to znamená numerické matice. ELEMENT Je termín. Termín je vhodné si zapamätať, bude sa s ním často stretávať, nie je náhoda, že som ho zvýraznil tučným písmom.
Označenie: matice sú zvyčajne označené veľkými latinskými písmenami
Príklad: Uvažujme maticu dva by tri:
![]()
Táto matica pozostáva zo šiestich prvky:
Všetky čísla (prvky) vo vnútri matice existujú samy osebe, to znamená, že nemôže existovať žiadne odčítanie: ![]()
Je to len tabuľka (množina) čísel!
Tiež sa dohodneme neprerobiťčísla, pokiaľ nie je vo vysvetlivkách uvedené inak. Každé číslo má svoje vlastné umiestnenie a nie je možné ho zamiešať!
Príslušná matica má dva riadky: 
a tri stĺpce: 
ŠTANDARD: keď hovoríme o veľkosti matice, potom najprv uveďte počet riadkov a až potom - počet stĺpcov. Práve sme rozdelili maticu dva na tri.
Ak je počet riadkov a stĺpcov matice rovnaký, nazýva sa matica námestie, napríklad:  -matica tri na tri.
-matica tri na tri.
Ak má matica jeden stĺpec alebo jeden riadok, potom sa také matice nazývajú vektory.
V skutočnosti poznáme koncept matice už od školy, vezmime si napríklad bod so súradnicami „x“ a „hra“ :. V zásade sú súradnice bodu zapísané do matice jedna po dvoch. Mimochodom, tu je príklad, prečo je poradie čísel dôležité: a sú to dva úplne odlišné body roviny.
Teraz prejdeme priamo k štúdiu akcie s maticami:
1) Prvá akcia. Odstránenie mínusu z matice (pridanie mínusu do matice).
Späť k našej matici  ... Ako ste si mohli všimnúť, v tejto matici je príliš veľa záporných čísel. To je veľmi nepohodlné z hľadiska vykonávania rôznych akcií s maticou, je nepohodlné písať toľko mínusov a dizajnovo to vyzerá škaredo.
... Ako ste si mohli všimnúť, v tejto matici je príliš veľa záporných čísel. To je veľmi nepohodlné z hľadiska vykonávania rôznych akcií s maticou, je nepohodlné písať toľko mínusov a dizajnovo to vyzerá škaredo.
Presuňte mínus mimo maticu zmenou znamienka KAŽDÉHO prvku matice:
Na nule, ako chápete, sa znamenie nemení, nula - v Afrike je nula.
Opačný príklad:  ... Vyzerá to škaredo.
... Vyzerá to škaredo.
Pridajme mínus do matice zmenou znamienka KAŽDÉHO maticového prvku:

No dopadlo to oveľa krajšie. A čo je najdôležitejšie, bude jednoduchšie vykonávať akékoľvek akcie s maticou. Pretože existuje také matematické ľudové znamenie: čím viac mínusov, tým viac zmätkov a chýb.
2) Druhá akcia. Vynásobenie matice číslom.
Príklad:
![]()
Je to jednoduché. Na vynásobenie matice číslom potrebujete každý prvok matice sa vynásobí daným číslom. V tomto prípade tri najlepšie.
Ďalší užitočný príklad:
 - násobenie matice zlomkom
- násobenie matice zlomkom
Pozrime sa, čo treba urobiť ako prvé. NETREBA:
Nie je potrebné zadávať zlomok do matice, po prvé to len komplikuje ďalšie akcie s maticou, a po druhé, učiteľovi to sťažuje kontrolu riešenia (najmä ak  - konečná odpoveď na úlohu).
- konečná odpoveď na úlohu).
A hlavne, NETREBA rozdeľte každý prvok matice mínus sedem:

Z článku Matematika pre figuríny alebo kde začať, pamätáme si, že desatinné zlomky s čiarkou vo vyššej matematike sa pokúšajú všemožne vyhnúť.
Jediná vec, ktorá žiaduce V tomto prípade je potrebné zaviesť do matice mínus:

Ale ak VŠETKY maticové prvky boli deliteľné 7 bezo zvyšku, potom by bolo možné (a nevyhnutné!) rozdeliť.
Príklad:

V tomto prípade je možné a POTREBNÉ vynásobte všetky prvky matice, pretože všetky čísla v matici sú deliteľné 2 bezo zvyšku.
Poznámka: v teórii vyššej matematiky neexistuje školský koncept „delenia“. Namiesto výrazu „rozdeľte to týmto“ môžete vždy povedať „vynásobte to zlomkom“. To znamená, že delenie je špeciálny prípad násobenia.
3) Tretia akcia. Transpozícia matice.
Aby ste mohli transponovať maticu, musíte zapísať jej riadky do stĺpcov transponovanej matice.
Príklad:
Transponovať maticu
Tu je iba jeden riadok a podľa pravidla musí byť zapísaný do stĺpca:
- transponovaná matica.
Transponovaná matica je zvyčajne označená horným indexom alebo pomlčkou v pravom hornom rohu.
Príklad krok za krokom:
Transponovať maticu 
Najprv prepíšeme prvý riadok do prvého stĺpca:

Potom prepíšeme druhý riadok do druhého stĺpca: 
Nakoniec prepíšeme tretí riadok do tretieho stĺpca:

Pripravený. Zhruba povedané, transponovať znamená obrátiť maticu na jednu stranu.
4) Akcia štyri. Súčet (rozdiel) matíc.
Súčet matíc je jednoduchá operácia.
NIE VŠETKY DIE SA MOHU ZLOŽIŤ. Na vykonanie sčítania (odčítania) matíc je potrebné, aby mali rovnakú VEĽKOSŤ.
Napríklad, ak je daná matica dvoch proti dvom, potom ju možno pridať iba s maticou dva po dvoch a žiadnou inou! 
Príklad:
Pridajte matice ![]() a
a ![]()
Na pridanie matíc je potrebné pridať ich zodpovedajúce prvky:

Pre rozdiel matíc je pravidlo podobné, je potrebné nájsť rozdiel zodpovedajúcich prvkov.
Príklad:
Nájdite rozdiel v maticiach ![]() ,
, ![]()

A ako tento príklad vyriešiť jednoduchšie, aby ste sa nenechali zmiasť? Odporúča sa zbaviť sa zbytočných mínusov, preto do matice pridáme mínus:

Poznámka: v teórii vyššej matematiky neexistuje školský koncept „odčítania“. Namiesto toho, aby ste povedali „odčítajte to od tohto“, môžete vždy povedať „pridajte k tomu záporné číslo“. To znamená, že odčítanie je špeciálny prípad sčítania.
5) Akcia päť. Maticové násobenie.
Aké matice je možné vynásobiť?
Aby bola matica vynásobená maticou, potrebujete aby sa počet stĺpcov matice rovnal počtu riadkov matice.
Príklad:
Je možné vynásobiť maticu maticou?

To znamená, že tieto matice môžete znásobiť.
Ak sú však matice preusporiadané, potom je v tomto prípade násobenie už nemožné!

Násobenie preto nie je možné:

Nie je tak zriedkavé, aby sa s úlohami s trikom stretlo, keď bol študent požiadaný o znásobenie matíc, ktorých násobenie je evidentne nemožné.
Treba poznamenať, že v niektorých prípadoch je možné matice znásobiť obidvoma spôsobmi.
Napríklad pre matice je možné násobenie aj násobenie
 Správa a funkcie modemu Nie je dosť položiek
Správa a funkcie modemu Nie je dosť položiek Riešenie problémov s TLauncher
Riešenie problémov s TLauncher Prečo Instagram nehľadá polohu: hlavné dôvody?
Prečo Instagram nehľadá polohu: hlavné dôvody? Ako vymazať vyrovnávaciu pamäť v aplikácii vk
Ako vymazať vyrovnávaciu pamäť v aplikácii vk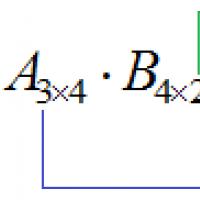 Základné operácie s maticami (sčítanie, násobenie, transpozícia) a ich vlastnosti
Základné operácie s maticami (sčítanie, násobenie, transpozícia) a ich vlastnosti Lítium -polymérové batérie
Lítium -polymérové batérie Identické prevody logických výrazov
Identické prevody logických výrazov