Nájdeme číslo N's Fibonacci v troch smeroch za prijateľný čas: základy dynamického programovania. Fibonacci Čísla: Fibonacci cyklus a rekurzión
Veľmi často na rôznych olympiads, sa zdá, že úlohy sú také, ktoré, ako sa predpokladá na prvý pohľad, možno vyriešiť jednoduchým bustovaním. Ale ak vypočítame číslo možné možnostiOkamžite sa uistím, že neefektívnosť tohto prístupu: Napríklad jednoduchou rekurzívnou funkciou nižšie bude konzumovať značné zdroje na 30. fibonacci, zatiaľ čo na olympijských hrách je čas rozhodovania často obmedzený na 1-5 sekundy.
INT FIBO (Int N) (ak (n \u003d\u003d 1 || n \u003d\u003d 2) (návrat 1;) inak (návrat FIBO (N - 1) + FIBO (N - 2);)
Premýšľajte o tom, prečo sa to stane. Napríklad na výpočet FIBO (30), najprv vypočítame FIBO (29) a FIBO (28). Ale zároveň náš program "zabudne", že Fibo (28) vypočítané Pri vyhľadávaní FIBO (29).
Hlavnou chybou tohto prístupu "na čele" je, že rovnaké hodnoty argumentov funkcií sa vypočítajú opakovane - a to sú dostatočné operácie náročné na zdroje. Zbavte sa opakujúcich sa výpočtov nám pomôže dynamické programovanie - Toto je recepcia, ak je táto úloha rozdelená na spoločné a opakujúce sa podušky, z ktorých každý je vyriešený len 1 čas - to výrazne zlepšuje efektívnosť programu. Táto metóda je podrobne opísaná v, existujú aj príklady riešenia iných úloh.
Najjednoduchšou možnosťou na zlepšenie našej funkcie je zapamätať si, aké hodnoty sme už vypočítali. Ak to chcete urobiť, musíte zadať ďalšie pole, ktoré bude slúžiť ako "cache" pre naše výpočty: Pred výpočtom novej hodnoty skontrolujeme, či bola vypočítaná predtým. Ak vypočítavame, budeme mať hotovú hodnotu z poľa, a ak nie je vypočítaná - budete musieť zvážiť ho na základe predchádzajúcich a zapamätať si do budúcnosti:
Cache int; INT FIBO (Int N) (ak (cache [n] \u003d\u003d 0) (ak (n \u003d\u003d 1 || n \u003d\u003d 2) (cache [n] \u003d 1;) inak (cache [n] \u003d FIBO (n - 1) + FIBO (N - 2);)) Späť Cache [N];)
Keďže v tejto úlohe vypočítať hodnotu N-mysle, budeme zaručené, že bude zaručená (n-1) -e, nebude ťažké prepísať vzorec do iteratívneho formulára - jednoducho vyplníme naše pole v a do požadovanej bunky:
<= n; i++) { cache[i] = cache + cache; } cout << cache;
Teraz si môžeme všimnúť, že keď vypočítame hodnotu F (n), hodnota F (n-3) je už zaručená nikdy nebude potrebovať. To znamená, stačí, aby sme uložili iba dve hodnoty v pamäti - F (n - 1) a f (n-2). Okrem toho, akonáhle vypočítali f (n), skladovanie F (n-2) stráca akýkoľvek význam. Pokúsme sa napísať tieto úvahy vo forme kódu:
// dva predchádzajúce hodnoty: Int cache1 \u003d 1; Int cache2 \u003d 1; // Nová hodnota Int cache3; pre (int i \u003d 2; i<= n; i++) { cache3 = cache1 + cache2; //Вычисляем новое значение //Абстрактный cache4 будет равен cache3+cache2 //Значит cache1 нам уже не нужен?.. //Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации. //cache5 = cache4 - cache3 => Trochu stratí relevantnosť cache2, t.j. Mal by byť cache1 // inými slovami, cache1 - f (n-2), cache2 - f (n-1), cache3 - f (n). // nechať n \u003d n + 1 (číslo, ktoré vypočítame v nasledujúcej iterácii). Potom N-2 \u003d N-3, N-1 \u003d N-2, N \u003d N-1. // V súlade s novými realitou prepisujeme hodnoty našich premenných: cache1 \u003d cache2; cache2 \u003d cache3; ) Cout<< cache3;
Skúsený programátor je zrejmé, že kód je vyšší, vo všeobecnosti, nezmysel, pretože cache3 sa nikdy nepoužíva (okamžite zaznamenáva v cache2) a môžete prepísať celú iteráciu pomocou iba jedného výrazu:
Cache \u003d 1; cache \u003d 1; pre (int i \u003d 2; i<= n; i++) { cache = cache + cache; //При i=2 устареет 0-й элемент //При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый //При i=4 последним элементом мы обновляли cache, значит ненужное старьё сейчас в cache //Интуитивно понятно, что так будет продолжаться и дальше } cout << cache;
Pre tých, ktorí nemôžu pochopiť, ako sa má kúzlo s zvyškom z divízie, alebo len chce vidieť viac nezjavujúceho vzorca, existuje ďalšie riešenie:
Int x \u003d 1; int y \u003d 1; pre (int i \u003d 2; i< n; i++) { y = x + y; x = y - x; } cout << "Число Фибоначчи: " << y;
Snažte sa sledovať vykonanie tohto programu: Uistite sa, že algoritmus opravíte.
P.S. Všeobecne platí, že existuje jeden vzorec pre výpočet ľubovoľného počtu Fibonacci, čo nevyžaduje žiadne iterácie alebo rekurziu:
Const dvojitá SQRT5 \u003d SQRT (5); CONST DOUNTH PHI \u003d (SQRT5 + 1) / 2; INT FIBO (INT N) (návrat INT (PHI, N) / SQRT5 + 0,5);)
Ale ako môžete uhádnuť, úlovok je, že cena výpočtu stupňov neuropálnych čísel je pomerne veľká, rovnako ako ich chyba.
Fibonacci čísla - Toto je niekoľko čísel, v ktorých sa každé ďalšie číslo rovná súčtu dvoch predchádzajúcich: 1, 1, 2, 3, 5, 8, 13, .... Niekedy riadok začína od nuly: 0, 1, 1, 2, 3, 5, .... V tomto prípade budeme dodržiavať prvú možnosť.
Vzorec:
F 1 \u003d 1
F 2 \u003d 1
F n \u003d f n-1 + f n-2
Príklad výpočtu:
F 3 \u003d F 2 + F 1 \u003d 1 + 1 \u003d 2
F 4 \u003d F 3 + F2 \u003d 2 + 1 \u003d 3
F 5 \u003d F 4 + F 3 \u003d 3 + 2 \u003d 5
F 6 \u003d F 5 + F 4 \u003d 5 + 3 \u003d 8
...
Výpočet n-th počtu riadkov Fibonacci pomocou cyklu
- Priraďte prvé prvé prvky série na premenné FIB1 a FIB2, to znamená, priraďte jednotku premennej.
- Požiadajte o číslo používateľa prvku, ktorého hodnota, ktorú chce dostať. Priraďte variabilné číslo n.
- Vykonajte tieto akcie n - 2-krát, pretože prvé dva prvky sú už zohľadnené: \\ t
- Fix Fib1 a Fib2 priradením výsledku premennej pre dočasné uskladnenie údajov, napríklad FIB_SUM.
- Variabilná Fib1 Priraďte hodnotu Fib2.
- Variabilná Fib2 Priraďte hodnotu FIB_SUM.
- Zobrazte Fib2.
Poznámka. Ak používateľ zadá 1 alebo 2, karosérie cyklu sa nikdy nevykoná, zobrazí sa pôvodná hodnota Fib2.
fib1 \u003d 1 Fib2 \u003d 1 n \u003d vstup () n \u003d INT (n) i \u003d 0< n - 2 : fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print (fib2)
Možnosť Compact Code:
fib1 \u003d Fib2 \u003d 1 n \u003d Int (vstup ( "Počet prvkov radu Fibonacci:")) - 2 Kým N\u003e 0: FIB1, FIB2 \u003d FIB2, FIB1 + FIB2 N - \u003d 1 Tlač (Fib2)
Výstup fibonacci čísiel s cyklom
V tomto prípade sa zobrazí nielen hodnota základového prvku série Fibonacci, ale aj všetky čísla k nej vrátane. Na tento účel je výstup hodnoty FIB2 umiestnený v cykle.
fib1 \u003d Fib2 \u003d 1 n \u003d Int (vstup ()) Ak n< 2 : quit() print (fib1, end= " " ) print (fib2, end= " " ) for i in range (2 , n) : fib1, fib2 = fib2, fib1 + fib2 print (fib2, end= " " ) print ()
Príklad vykonania:
10 1 1 2 3 5 8 13 21 34 55
Rekurzívny výpočet n-th číslo fibonacciho radu
- Ak n \u003d 1 alebo n \u003d 2, vráťte sa na jednotku povodia, pretože prvé a druhé prvky rastu Fibonacci sú rovnaké.
- Vo všetkých ostatných prípadoch spôsobujú rovnakú funkciu s argumentmi N - 1 a N - 2. Výsledok dvoch hovorov na zloženie a návrat do pobočky volajúceho programu.
def Fibonacci (n): Ak N v (1, 2): RETURN 1 RETURN FIBONACCI (N-1) + FIBONACCI (N-2) Tlač (Fibonacci (10))
Predpokladajme, že n \u003d 4. Potom bude existovať rekurzívny volanie Fibonacci (3) a Fibonacci (2). Druhá bude vrátiť jednotku a prvá povedie k ďalším ďalším výzvam funkcie: Fibonacci (2) a Fibonacci (1). Obe hovory budú vrátené jedným, v množstve budú dva. Volanie Fibonacci (3) sa teda vráti číslo 2, ktoré je zhrnuté s číslom 1 z volania Fibonacci (2). Výsledok 3 sa vracia do hlavnej vetvy programu. Štvrtý prvok rozsahu Fibonacci je tri: 1 1 2 3.
Programátori čísla Fibonacci by mali mať už fond. Príklady ich výpočtov sa používajú všade. Všetko od skutočnosti, že tieto čísla poskytujú najjednoduchší príklad rekurzie. A sú dobrým príkladom dynamického programovania. Je však potrebné ich vypočítať v reálnom projekte? Nie. Ani rekurziou ani dynamické programovanie nie sú ideálne možnosti. A nebola uzavretá vzorca, ktorá využíva čísla plávajúceho bodu. Teraz vám poviem, ako správne. Ale najprv prejdite všetkými dobre známymi riešeniami.Kód je určený pre Python 3, hoci musí ísť na Python 2.
Začať s - pripomínam definíciu:
F n \u003d f n-1 + f n-2
A f 1 \u003d f2 \u003d 1.
Uzavretý vzorec
Poďme chýbajú detaily, ale tí, ktorí sa chcú oboznámiť s uzavretím vzorca. Myšlienkou je predpokladať, že existuje určitý x pre ktorý f n \u003d x n, a potom nájsť x.Čo znamená
ZNÍŽENIE X N-2
Riešime štvorcovú rovnicu:
Odkiaľ rastie "zlatá časť" φ \u003d (1 + √5) / 2. Nahradenie počiatočných hodnôt a vykonalo viac výpočtov, dostaneme:
Ako sa používame na výpočet f n.
Z __FUTURE__ Import Division Import Matematika Def Fib (n): SQRT5 \u003d Math.sqrt (5) PHI \u003d (SQRT5 + 1) / 2 Return INT (PHI ** N / SQRT5 + 0,5)
Dobré:
Rýchlo a len pre malé n
Chudobný:
Chcel plávajúce činnosti. Pre veľké n, bude potrebná veľká presnosť.
Zlo:
Použitie integrovaných čísel na výpočet f n je krásne z matematického hľadiska, ale škaredé - s počítačom.
Rekurzia
Najzrejmejšie rozhodnutie, ktoré ste už videli mnohokrát - s najväčšou pravdepodobnosťou, ako príklad toho, čo je rekurzia. Opakujem to znova na úplnosť. V pythone môže byť zaznamenaný v jednom riadku:FIB \u003d LAMBDA N: FIB (N - 1) + FIB (N - 2), AK N\u003e 2 ELSE 1
Dobré:
Veľmi jednoduchá implementácia opakovaná matematická definícia
Chudobný:
Čas exponenciálneho vykonávania. Pre veľké n veľmi pomaly
Zlo:
Prepad zásobníka
Pamäť
Riešenie s rekurziou má veľký problém: pretínanie výpočtov. Keď sa nazýva FIB (N), vypočíta sa FIB (N-1) a FIB (N-2). Ale keď je Fib považovaný (N-1), bude nezávisle vypočítať Fib (N-2) - to znamená, FIB (N-2) sa vypočíta dvakrát. Ak budete pokračovať v argumentoch, bude zrejmé, že FIB (N-3) sa vypočíta trikrát atď. Príliš veľa križovatiek.Preto potrebujete zapamätať si výsledky, aby ste ich opäť nepočítali. Čas a pamäť tohto riešenia sa strávi lineárne. Pri riešení používam slovník, ale môžete použiť jednoduché pole.
M \u003d (0: 0, 1: 1) DEF FIB (N): Ak N v M: RETURN M [N] M [N] \u003d FIB (N-1) + FIB (N-2) RETURN RETURN M [N]
(V pythone, môže sa tiež vykonať pomocou dekorácie, functools.lru_cache.)
Dobré:
Zamerať sa na rekurziu do riešenia zapamätania. Vypne exponenciálny čas na vykonanie lineárneho, pre ktoré trávi viac pamäte.
Chudobný:
Trávi veľa pamäte
Zlo:
Je možné pretekať stoh, ako v rekurcii
Dynamické programovanie
Po rozhodnutí s zapamätaním sa stáva jasným, že nemusíme nie všetky predchádzajúce výsledky, ale len posledné dve. Namiesto toho, namiesto toho, aby ste začali s FIB (N) a vrátiť sa, môžete začať s FIB (0) a ísť dopredu. Ďalší kód má lineárny čas vykonanie a používanie pamäte je pevné. V praxi bude rýchlosť riešenia ešte vyššia, pretože neexistujú žiadne rekurzívne výzvy funkcií a súvisiace operácie. A kód vyzerá jednoduchšie.Toto riešenie je často uvedené ako príklad dynamického programovania.
Def Fib (n): A \u003d 0 B \u003d 1 pre __ v rozsahu (n): A, B \u003d B, A + B NÁVRAT
Dobré:
Funguje rýchlo pre malé n, jednoduchý kód
Chudobný:
Stále lineárny čas vykonávania
Zlo:
Áno, nič nie je nič.
MATRIX ALGEBRA
A nakoniec, najmenej osvetlený, ale najsprávnejšie riešenie, kompetentne používajú čas a pamäť. Môže sa tiež rozšíriť na akúkoľvek homogénnu lineárnu sekvenciu. Myšlienka pri používaní matríc. Je to dosť jednoduché, aby to videliA generalizácia to hovorí
Dve hodnoty pre X, ktoré sme získali skôr, z ktorých jeden predstavoval reprezentovaný prierez zlata, sú eiggenvalues \u200b\u200bmatrice. Preto iný spôsob výstupu uzavretého vzorca je použitie matricovej rovnice a lineárnej algebry.
Čo je teda užitočné takéto znenie? Skutočnosťou, že výstava môže byť vykonaná pre logaritmický čas. To sa vykonáva prostredníctvom výstavby námestia. Spodný riadok je to
Tam, kde sa prvý výraz používa na párty, druhý pre nepárny. Zostáva len na organizovanie multiplikácií matríc a všetko je pripravené. Získa sa nasledujúci kód. Zorganizoval som rekurzívnu implementáciu POW, pretože je ľahšie pochopiť. Iteratívna verzia Pozrite sa sem.
DEF POW (X, N, I, MULT): "" "vráti x na stupeň n. Predpokladá, že som jediná matrica, ktorá sa líši s MULT, a n je kladná celá" "", ak n \u003d\u003d 0: návrat I elif n \u003d\u003d 1: návrat x iný: y \u003d pow (x, n // 2, i, mult) y \u003d mult (y, y), ak n% 2: y \u003d mult (x, y) návrat y def IDENTITY_MATRIX (N): "" "Vráti jednu matricu n na n" "" R \u003d zoznam (rozsah (n)) Návrat [pre J v R] Def Matrix_Multiply (A, B): BT \u003d Zoznam (ZIP (* B )) Return [for Row_a v a] DEF FIB (N): F \u003d POW ([,], N, IDENTITY_MATRIX (2), MATRIX_MULTIPY) návrat F
Dobré:
Pevná pamäť, logaritmický čas
Chudobný:
Kód je komplikovanejší
Zlo:
Musia pracovať s matricami, aj keď nie sú tak zlé
Porovnanie rýchlosti
Je to len variant dynamického programovania a matrice. Ak ich porovnávajú počtom znakov, medzi n, ukázalo sa, že riešenie matrice je lineárne a roztok s dynamickým programovaním je exponenciálne. Praktický príklad - výpočet FIB (10 ** 6), číslo, ktoré bude mať viac ako dvesto tisíc znakov.N \u003d 10 ** 6
Výpočet FIB_MATRIX: FIB (N) má iba 208988 číslic, výpočet trvalo 0,24993 sekúnd.
Výpočet FIB_DYNAMIC: FIB (N) je len 208988 číslic, výpočet trvalo 11,83377 sekúnd.
Teoretické komentáre
Nie je priamo dotýka vyššie uvedeného kódu, táto poznámka je stále nejaký záujem. Zvážte nasledujúci graf:
Vypočítajte počet ciest n z A do B. Napríklad, pre n \u003d 1 máme jednu cestu, 1. Pre n \u003d 2, opäť máme jedným spôsobom, 01. Pre n \u003d 3 máme dva spôsoby, 001 a 101 , Je celkom jednoduché ukázať, že počet ciest n od A do B sa rovná presnosti f n. Po odpísaní usporiadania matice pre graf dostaneme rovnakú matricu, ktorá bola opísaná vyššie. Toto je dobre známy výsledok z teórie grafov, ktorý pre danú maticu susednosti A, výskyt C n je počet ciest n v stĺpci (jedna z úloh uvedených vo filme "Umnitsa bude lov" ).
Prečo sú takéto označenia na pojmoch? Ukazuje sa, že keď zvažuje nekonečnú sekvenciu znakov na nekonečnom mieste v oboch stranách sekvencie dráh na stĺpci, dostanete niečo nazývané "finálne posuny typu", čo je typ symbolického systému reproduktorov. Konkrétne, tento konečný typ typu je známy ako "posun Zlatého úseku" a je nastavený ako súbor "zakázaných slov" (11). Inými slovami, dostaneme nekonečné binárne sekvencie v oboch smeroch a žiadne páry ich budú priľahlé. Topologická entropia tohto dynamického systému sa rovná zlatej časti φ. Zaujímalo by ma, ako sa toto číslo pravidelne objavuje v rôznych oblastiach matematiky.
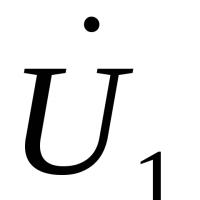 Magnetometria v najjednoduchšej verzii Ferrozond sa skladá z feromagnetického jadra a dvoch cievok na ňom
Magnetometria v najjednoduchšej verzii Ferrozond sa skladá z feromagnetického jadra a dvoch cievok na ňom Efektívny hľadaný kurz práce
Efektívny hľadaný kurz práce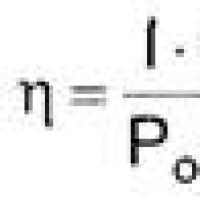 Hlavné charakteristiky a parametre fotodiódy
Hlavné charakteristiky a parametre fotodiódy Ako upraviť PDF (päť aplikácií na zmenu súborov PDF) Ako odstrániť jednotlivé stránky z PDF
Ako upraviť PDF (päť aplikácií na zmenu súborov PDF) Ako odstrániť jednotlivé stránky z PDF Prečo sa okno vystreleného programu dlho rozvíjalo?
Prečo sa okno vystreleného programu dlho rozvíjalo? DXF2TXT - Export a preklad textu od AutoCADu na zobrazenie bodu DWG Traffic v txt
DXF2TXT - Export a preklad textu od AutoCADu na zobrazenie bodu DWG Traffic v txt Čo robiť, ak kurzor myši zmizne
Čo robiť, ak kurzor myši zmizne