Реферат: Апроксимація характеристик нелінійних елементів і аналіз ланцюгів при гармонійних впливах. §3.2 Апроксимація характеристик нелінійних елементів Апроксимація характеристик нелінійних елементів
Як зазначалося раніше, зручними характеристиками нелінійних елементів не є рівняння зв'язку, а вольтамперная характеристика активного опору  або
або  , Або залежність
, Або залежність  - для нелінійної індуктивності (ампервеберная характеристика), або завісімостьq (u) - для нелінійної ємності (вольткулонная характеристика) (рис.3.8).
- для нелінійної індуктивності (ампервеберная характеристика), або завісімостьq (u) - для нелінійної ємності (вольткулонная характеристика) (рис.3.8).
Рис.3.8. Види характеристик нелінійних елементів
Однак, графічна форма характеристик нелінійних елементів (рис.3.8.) Не дозволяє використовувати залежності (3.1-3.15), для складання рівнянь роботи схем з нелінійними елементами. Тому одним з найважливіших завдань, яка виникає при аналізі коливань в схемах, що містять нелінійні елементи, полягає в апроксимації нелінійних характеристик. Найбільшого поширення аппроксимаций нелінійних характеристик отримали поліноміальна і кусочно-лінійна, а також апроксимація за допомогою різних видів трансцендентних функцій.
При аналізі нелінійних схем можливість отримати правильний результат істотно залежить як від правильності вибору методу апроксимації, так і від виразу апроксимуючої функції нелінійного елемента. Виникає певне протиріччя - чим точніше апроксимація нелінійного елемента, тим складніше отримати потрібне аналітичне вираз характеристики нелінійного елемента. Але крім цього, складніше побудувати і рішення нелінійного рівняння, опісиваюшего коливання в такій нелінійної системі, за допомогою обраного виразу апроксимуючої функції. Тому правильний вибір апроксимації нелінійної характеристики дозволяє істотно спростити побудову рішення нелінійного рівняння. Крім того необхідно відзначити, що дуже часто одну і ту ж характеристику нелінійного елемента доводиться по-різному апроксимувати в залежності від того, в яких умовах працює нелінійний елемент і які питання повинні бути досліджені. Тому, способи апроксимації вибирають в кожному конкретному випадку дослідження коливань в схемах з нелінійними елементами різними.
Розглянемо способи апроксимації різних функцій нелінійних елементів. До найбільш поширених способів апроксимації нелінійних елементів відносять такі:
поліноміальна апроксимація ─ представлення нелінійної характеристики за допомогою статечного ряду,
кусочно-лінійна апроксимація ─ представлення функції, що апроксимується відрізками прямих ліній,
апроксимація за допомогою різних видів трансцендентних функцій.
Поліноміальна апроксимація. Якщо будь-яка з нелінійних характеристик задана аналітичним виразом, то в околиці робочої точки функція може бути представлена \u200b\u200bрозкладанням в ряд Тейлора (  в околиці точки х 0)
в околиці точки х 0)
 ,
(3.16)
,
(3.16)
де R - залишок в розкладанні в ряд Тейлора, яким нехтують при апроксимації.
Якщо ж характеристика задана графічно (рис.3.9), то апроксимацію можна здійснити укороченим статечним рядом (поліном), обмежуючи його другої - п'ятої ступенем

Рис.3.9. Графічне представлення нелінійної характеристики
Для визначення коефіцієнтів а k вимагаємо, щоб при значеннях змінної x k в лівій частині полінома (3.17) виходили значення функції y k.
Складаємо систему рівнянь:
 , де
, де  .
(3.18)
.
(3.18)
У цій системі рівнянь y n, у 0, x n, x 0 - відомі величини, тому цю систему можна вирішити за методом Крамера, щодо коефіцієнтів a k.
Якщо x \u003d x 0 + S (х 0 постійний зсув, а S малий сигнал), то
де α - диференційний параметр нелінійного елемента. Таким чином, можна відзначити, що перший коефіцієнт a 1 полиномиальной апроксимації нелінійної характеристики (3.17) збігається з диференціальним параметром нелінійного елемента. Крім того зазначимо, що якщо х \u003d 0 лежить всередині інтервалу (х 5 х 1) апроксимації нелінійної характеристики поліномом, то коефіцієнт а 0 визначає значення функції на початку координат (тобто якщо ми розглядаємо як нелінійної характеристики i \u003d φ ( u), то коефіцієнт а 0 \u003d i (0) визначається як значення струму при u \u003d 0.
Кусково-лінійна апроксимація. Кусково-лінійна апроксимація заснована на заміні реальної характеристики нелінійного елемента окремими ділянками, які замінюються відрізками прямих ліній (рис.3.10).

Рис.3.10. Кусково-лінійна апроксимація нелінійного елемента
Точність кусочно-лінійного наближення залежить від кількості інтервалів, замінних відрізками прямих в заданому інтервалі використання кусочно-лінійної апроксимації. Чим на більшу кількість відрізків прямих розбитий інтервал, для якого ми застосовуємо кусочно-лінійне наближення, тим вище точність збігу з реальною нелінійної характеристикою, але при цьому сушественно ускладнюється аналіз коливань в такій системі. Для спрощення розрахунків бажано обмежуватися мінімальною кількістю відрізків прямих, що заміщають нелінійну характеристику. Наприклад, динамічну прохідну характеристику тріода (рис.3.10) можна апроксимувати з достатнім ступенем точності всього лише трьома відрізками прямих ліній:
 .
(3.20)
.
(3.20)
Заміна нелінійних ділянок характеристик нелінійних елементів відрізками прямих, прозволяет вважати і самі характеристики лінійними, а це значить, що застосовні тепер все методи лінійної теорії ланцюгів. Протягом лінійних ділянок нелінійні елементи замінюються на лінійні, з характеристиками рівними їх диференціальним величинам.
Апроксимація нелінійних характеристик за допомогою трансцендентних функцій. Іноді характеристики нелінійних елементів апроксимують трансцендентними функціями рис.3.11. Як аппроксимирующих трансцендентних функцій застосовуються експоненти і їх суми, тригонометричні, зворотні тригонометричні, гіперболічні і інші функції. наприклад,
або  .
(3.21)
.
(3.21)

Рис.3.11. Приклади апроксимації нелінійних характеристик
трансцендентними функціями
Як правило, ВАХ нелінійних елементовi \u003d F (u) отримують експериментально, тому найчастіше вони задані у вигляді таблиць або графіків . щоб мати справу з аналітичними виразами , доводиться вдаватися до апроксимації.
Обозначімзаданную таблично або графічно ВАХ нелінійного елементаi \u003d F V (u), а аналітичну функцію, аппроксимирующуюзадану характеристику, i \u003d F (u, a 0, a 1, a 2, ..., a N ). де a 0, a 1, ..., a N – коефіцієнти цієї функції, які потрібно знайти в результаті апроксимації.
А) У методі Чебишева коефіцієнти a 0 , a 1 , … , a N функції F (u) знаходяться з умови:
т. е. вони визначаються в процесі мінімізації максимального ухилення аналітичної функції від заданої. тут u k, k \u003d 1, 2, ..., G - обрані значення напруги u.
При среднеквадратичном наближенні коефіцієнти a 0 , a 1 , …, a N повинні бути такими, щоб мінімізувати величину:
 , (2.6)
, (2.6)
Б) Наближення функції по Тейлору засноване на уявленні функції i \u003d F (u) поруч Тейлора в околиці точкіu \u003d U 0:
і визначенні коефіцієнтів цього розкладання. якщо обмежитися першими двома членами розкладання в ряд Тейлора, то мова піде про заміну складної нелінійної залежності F (u) більш простий лінійною залежністю . така заміна називаємося лінеаризацією характеристик.
перший член розкладання F (U 0) \u003d I 0 являє собою постійний струм в робочій точці при u \u003d U 0, а другий чльон
диференціальну крутизну вольт-амперної характеристики в робочій точці , Т. Е. При u \u003d U 0 .
В) найбільш поширеним способом наближення заданої функції є інтерполяція (Метод вибраних точок), при якій коефіцієнти a 0 , a 1 , …, a N апроксимуючої функції F (u) знаходяться з рівності цієї функції і заданої F x (u) в обраних точках (Вузлах інтерполяції) u k \u003d 1, 2, ..., N + 1.
Д) Статечна (поліноміальна ) Апроксимація. Таку назву отримала апроксимація ВАХ статечними полиномами:
іноді буває зручно вирішувати задачу апроксимації заданої характеристики в околиці точкіU 0 , званої робочої. тоді використовують статечної поліном
статечна апроксимація широко використовується при аналізі роботи нелінійних пристроїв, на які подаються щодо малі зовнішні впливи , тому потрібно досить точне відтворення нелінійності характеристики в околиці робочої точки.
Е) Кусково-лінійна апроксимація. У тих випадках, коли на нелінійний елемент впливають напруги з великими амплітудами, можна допустити більш наближену заміну характеристики нелінійного елемента і використовувати більше прості аппроксимирующие функції . найбільш часто при аналізі роботи нелінійного елемента в такому режимі реальна характеристика замінюється відрізками прямих ліній з різними нахилами .
З математичної точки зору це означає, що на кожному замінюють ділянці характеристики використовуються статечні поліноми першого ступеня ( N \u003d 1 ) З різними значеннями коефіцієнтів a 0 , a 1 , … , a N.
Таким чином, задача апроксимації ВАХ нелінійних елементів полягає у виборі виду апроксимуючої функції і визначення її коефіцієнтів одним із зазначених вище методів.
При дослідженні властивостей електричних ланцюгів явищем гістерезису, як правило, можна знехтувати. Лише при дослідженні ланцюгів, в основі дії яких лежить це явище (наприклад, роботи запам'ятовуючих магнітних пристроїв з прямокутною петлею гістерезису), гістерезис необхідно враховувати.
На рис. 15.11, а зображена типова симетрична характеристика у \u003d f (x).
Для нелінійної індуктивності роль х грає миттєве значення індукції роль у - миттєве значення напруженості поля Н. Для нелінійного конденсатора у - це напруга - заряд q. Для нелінійних резисторів (наприклад, тірітових опорів) роль х грає напруга, у - струм.
Існує велика кількість різних аналітичних виразів, в тій чи іншій мірі придатних для аналітичного опису характеристик нелінійних елементів. При виборі найбільш підходящого аналітичного виразу для функції у \u003d f (x) виходять не тільки з того, що крива, описувана аналітичним виразом, повинна досить близько усіма своїми точками розташуватися до досвідченим шляхом отриманої кривої в передбачуваному діапазоні переміщень робочої точки на ній, але враховують і ті можливості, які вбрання аналітичний вираз дає при аналізі властивостей електричних ланцюгів.

Надалі для аналітичного опису симетричних характеристик на кшталт рис. 15.11, а будемо користуватися гіперболічним синусом:
У цьому виразі - числові коефіцієнти; а виражається в тих одиницях, що - в одиницях, зворотних одиницям так що твір є величина безрозмірна. Для визначення невідомих коефіцієнтів слід на отриманої дослідним шляхом залежно у \u003d f (x) в передбачуваному робочому діапазоні довільно вибрати дві найбільш характерні точки, через які повинна пройти аналітична крива, підставити координати цих точок в рівняння (15.1) і потім вирішити систему з двох рівнянь з двома невідомими.
Нехай координати цих точок (рис. 15.11, а). тоді
ставлення
Трансцендентне рівняння (15.2) служить для визначення коефіцієнта. отже,
![]()
Приклад 147. Крива намагнічування трансформаторної сталі зображена на рис. 15.11, б. Знайти коефіцієнти а і.
Рішення. Вибираємо дві точки на кривій:
За рівняння (15.2) маємо Задаємося довільними значеннями і виробляємо підрахунки:

За результатами підрахунків будуємо криву і по ній знаходимо. далі визначаємо
Пунктирна крива на рис. 15.11, б побудована за рівнянням. § 15.14. Поняття про функції Бесселя. При аналізі нелінійних ланцюгів широко використовують функції Бесселя, які є рішенням рівняння Бесселя

Функції Бесселя висловлюють статечними рядами і для них складені таблиці. Функцію Бесселя від аргументу позначають, де - порядок функції Бесселя. Загальна вираз для у вигляді статечного ряду можна записати так:
Таблиця 15.1

Для аналізу проходження сигналів через ланцюга, що містять нелінійний елемент, необхідно задати його вольт-амперну характеристику (ВАХ) в аналітичній формі. Для двополюсного нелінійного елемента ВАХ характеризує залежність його струму від прикладеної напруги i(u); багатополюсні НЕ описуються прохідний характеристикою. Найбільш широко поширені способи подання нелінійних ВАХ у вигляді поліномів або лінійно-ламаних відрізків. Поліномінальної апроксимація використовується зазвичай при досить малих змінах вхідної напруги в околиці робочої точки, а лінійно-ламана - при великих.
Розглянемо апроксимацію в вигляді статечного полінома на прикладі біполярного транзистора, включеного за схемою з загальним емітером. Його прохідна ВАХ описується залежністю. Ступінь полінома, якій можна обмежити аппроксимирующую функцію, залежить від положення робочої точки і величини вхідної напруги. На рис.23 показаний графік функції, де Е отс - напруга база-емітер, відповідне відсічення струму.

У загальному випадку аппроксимирующий поліном має вигляд
де - струм колектора в робочій точці при - постійний зсув переходу база-емітер (робоча точка), - коефіцієнти полінома, причому

Коефіцієнт являє собою крутизну (похідну) характеристики в робочій точці, - першу похідну від крутизни (з коефіцієнтом 1/2) і т.д. Ясно, що коефіцієнти залежать від положення робочої точки нелінійного елемента, тобто від його режиму по постійному струму.
Розглянемо окремі випадки.
1.Рабочая точка знаходиться на лінійній ділянці характеристики, а зміни вхідного напруги такі, що миттєве значення струму не виходить за межі лінійної ділянки.
В цьому випадку при апроксимації можна обмежитися поліномом першого ступеня:
Часто коефіцієнт називають крутизною і позначають буквою S.
Даний вид апроксимації використовується при аналізі підсилювачів слабкого сигналу, а робоча точка зазвичай вибирається на середині самого крутого лінійної ділянки (точка на рис.23).
2.Рабочая точка розташована на нижньому нелінійному ділянці ВАХ (точка на рис.23), що має вигляд квадратичної параболи. При цьому передбачається, що миттєве значення вхідної напруги не заходить за точку, де - напруга відсічення нелінійного елемента (початок характеристики). В цьому випадку аппроксимирующий поліном можна обмежити другим ступенем:
де ![]() .
.
Якщо - крутизна ВАХ в робочій точці, то величину можна визначити з умови: ![]() ,. В цьому випадку ,
,. В цьому випадку ,
![]()
3.Робочий точка є точкою перегину характеристики, а зміни вхідного сигналу досить великі (див. Рис.24).

У точці перегину все похідні парного порядку дорівнюють нулю. Тому
Якщо, можна обмежитися поліномом третього ступеня без квадратичного члена (пунктир на рис.24):
напруга ![]() іноді називають напругою насичення. Ставлячи це напруга і знаючи величину, однозначно визначається величина:
іноді називають напругою насичення. Ставлячи це напруга і знаючи величину, однозначно визначається величина:
![]() ,
,
Апроксимація у вигляді кубічного полінома допустима при ![]() .
.
У всіх інших випадках положення робочої точки і зміни вхідного напруги поліномінальної апроксимація вимагає більш високої степені.Прі цьому аналіз ускладнюється і застосування статечного полінома для практичних розрахунків виявляється неефективним.
При дуже великі зміни сигналу більш доцільною виявляється кусочно-лінійна апроксимація. При цьому для побудови характеристики транзистора з ОЕ в режимі великого сигналу можна використовувати такі ідеалізації:
а) статичні вхідні ВАХ можна вважати незалежними від; нижній нелінійний ділянку випрямляється до перетину з віссю абсцис; ця точка визначає напругу; в цьому випадку передбачається однозначна залежність напруги від, тобто вихідні характеристики не залежать від того, при якому параметрі вони зняті (див. рис.25.);
академія Росії
Кафедра Фізики
Реферат на тему:
«Апроксимації ХАРАКТЕРИСТИК нелінійних ЕЛЕМЕНТІВ І АНАЛІЗ КІЛ ПРИ гармонійного впливу»
навчальні питання
1. Апроксимація характеристик нелінійних елементів
2. Графо-аналітичний та аналітичний методи аналізу
3. Аналіз ланцюгів методом кута відсічення
4. Вплив двох гармонійних коливань на безінерційний
нелінійний елемент
література
вступ
Для всіх розглянутих раніше лінійних ланцюгів справедливий принцип суперпозиції, з якого випливає просте і важливе наслідок: гармонійний сигнал, проходячи через лінійну стаціонарну систему, залишається незмінним за формою, набуваючи лише інші амплітуду і початкову фазу. Саме тому лінійна стаціонарна ланцюг не здатна збагатити спектральний склад вхідного коливання.
Особливістю НЕ, в порівнянні з лінійними, є залежність параметрів НЕ від величини прикладеної напруги або сили струму, що протікає. Тому на практиці при аналізі складних нелінійних ланцюгів користуються різними наближеними методами (наприклад, замінюють нелінійну ланцюг лінійної в області малих змін вхідного сигналу і використовують лінійні методи аналізу) або обмежуються якісними висновками.
Важливою властивістю нелінійних електричних ланцюгів є можливість збагачення спектру вихідного сигналу. Ця важлива особливість використовується при побудові модуляторів, перетворювачів частоти, детекторів і т. Д.
Рішення багатьох задач, пов'язаних з аналізом і синтезом радіотехнічних пристроїв і ланцюгів, вимагає знання процесів, що відбуваються при одночасному впливі на нелінійний елемент двох гармонійних сигналів. Це пов'язано з необхідністю перемноження двох сигналів при реалізації таких пристроїв, як перетворювачі частоти, модулятори, демодулятори і т. Д. Природно, що спектральний склад вихідного струму НЕ при бігармонічні впливі буде набагато багатшими, ніж при моногармоніческом.
Нерідко виникає ситуація, коли один з двох впливають на НЕ сигналів малий по амплітуді. Аналіз в цьому випадку значно спрощується. Можна вважати, що по відношенню до малого сигналу НЕ є лінійним, але зі змінним параметром (в даному випадку крутизною ВАХ). Такий режим роботи НЕ називається параметричним.
1. Апроксимація характеристик нелінійних елементів
При аналізі нелінійних ланцюгів (НЦ) зазвичай не розглядають процеси, що відбуваються всередині елементів, що складають цю ланцюг, а обмежуються лише зовнішніми їх характеристиками. Зазвичай це залежність вихідного струму від прикладеної вхідної напруги
, (1)яку прийнято називати вольт-амперної характеристикою (ВАХ).
Найпростіше - використовувати наявну табличну форму ВАХ для чисельних розрахунків. Якщо ж аналіз ланцюга повинен проводитися аналітичними методами, то виникає задача підбору такого математичного виразу, яке відображало б все найважливіші особливості експериментально знятої характеристики.
Це не що інше, як завдання апроксимації. При цьому вибір апроксимуючих виразів визначається як характером нелінійності, так і використовуваними розрахунковими методами.
Реальні характеристики мають досить складний вид. Це ускладнює їх точний математичний опис. Крім того, таблична форма подання ВАХ робить характеристики дискретними. У проміжках між цими точками значення ВАХ невідомі. Перш ніж переходити до апроксимації, необхідно якось визначитися з невідомими значеннями ВАХ, зробити її безперервної. Тут виникає задача інтерполяції (від лат. inter - між, polio - пригладжував) - це відшукання проміжних значень функції щодо деяких відомих її значень. Наприклад, відшукання значень
в точках лежачих між точками по відомих значеннях. Якщо, то аналогічна процедура носить завдання екстраполяції.Зазвичай апроксимують лише ту частину характеристики, яка є робочою областю, т. Е. В межах зміни амплітуди вхідного сигналу.
При апроксимації вольт-амперних характеристик необхідно вирішити два завдання: вибрати певну аппроксимирующую функцію і визначити відповідні коефіцієнти. Функція повинна бути простою і в той же час досить точно передавати апроксимується характеристику. Визначення коефіцієнтів апроксимуючих функцій здійснюється методами інтерполяції, середньоквадратичного або рівномірного наближення, які розглядаються в математиці.
Математично постановка задачі інтерполяції може бути сформульована таким чином.
знайти многочлен
ступені не більше n такий, що i = 0, 1, …, n, Якщо відомі значення вихідної функції в фіксованих точках, i = 0, 1, …, n. Доводиться, що завжди існує тільки один інтерполяційний многочлен, який може бути представлений в різних формах, наприклад у формі Лагранжа або Ньютона. (Розглянути самостійно на самопідготовки по рекомендованій літературі).Апроксимація статечними полиномами і кусочно-лінійна
Вона заснована на використанні добре відомих з курсу вищої математики рядів Тейлора і Маклорена і полягає в розкладанні нелінійної ВАХ
в безконечномірний ряд, що сходиться в деякій околиці робочої точки. Оскільки такий ряд фізично не реалізуємо, доводиться обмежувати число членів ряду, виходячи з необхідної точності. Статечна апроксимація застосовується при відносно малій зміні амплітуди впливу відносно.Розглянемо типову форму ВАХ будь-якого НЕ (рис. 1).
напруга
визначає положення робочої точки і, отже, статичний режим роботи НЕ.Мал. 1. Приклад типової ВАХ НЕ
Зазвичай апроксимується не вся характеристика НЕ, а лише робоча область, розмір якої визначається амплітудою вхідного сигналу, а положення на характеристиці - величиною постійного зміщення
. Аппроксимирующий поліном записується у вигляді, (2)де коефіцієнти
визначаються виразами.Апроксимація степеневим поліномом полягає в знаходженні коефіцієнтів ряду
. При заданій формі ВАХ ці коефіцієнти істотно залежать від вибору робочої точки, а також від ширини використовуваного ділянки характеристики. У зв'язку з цим доцільно розглянути деякі найбільш типові і важливі для практики випадки.1. Робоча точка розташована на середині лінійної ділянки (рис. 2).
Мал. 2. Робоча точка ВАХ - на середині лінійної ділянки
Ділянка на характеристиці, де закон зміни струму близький до лінійного, щодо неширокий, тому амплітуда вхідної напруги
не повинна виходити за межі цієї ділянки. В цьому випадку можна записати:, (3) - струм спокою; ; - диференціальна крутизна характеристики.Цей випадок можна застосувати тільки при слабкому сигналі
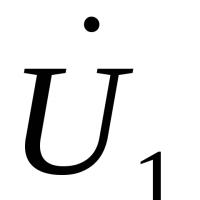 Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок
Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок Ефективний пошук роботи Курс з пошуку роботи
Ефективний пошук роботи Курс з пошуку роботи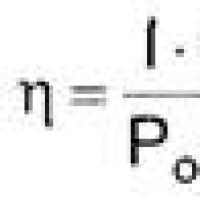 Основні характеристики і параметри фотодіода
Основні характеристики і параметри фотодіода Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF
Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF Чому згорнуте вікно програми довго розгортається?
Чому згорнуте вікно програми довго розгортається? DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt
DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt Що робити якщо пропав курсор миші
Що робити якщо пропав курсор миші