Регістр зсуву з лінійної зворотним зв'язком c. Теоретичні основи роботи. Для чого потрібні послідовності, що генеруються регістрами зсуву
Послідовності регістрів зсуву використовуються як в криптографії, так і в теорії кодування. Їх теорія прекрасно опрацьована, потокові шифри на базі регістрів зсуву були робочою конячкою військової криптографії задовго до появи електроніки.
Регістр зсуву зі зворотним зв'язком (далі РгСсОС) складається з двох частин: регістразсуву і функції зворотного зв'язку. Регістр зсуву являє собою послідовність бітів. Кількість бітів визначається довжиною зсувного регістру, Якщо довжина дорівнює n бітів, то регістр називається n-бітових зсувними регістром. Всякий раз, коли потрібно витягти біт, все біти зсувного регістру зсуваються вправо на 1 позицію. Новий крайній лівий біт є функцією всіх інших бітів регістра. На виході зсувного регістру виявляється один, зазвичай молодший значущий, біт. Періодом зсувного регістру називається довжина одержуваної послідовності до початку її повторення.
Малюнок 1. Регістр зсуву зі зворотним зв'язком
Регістри зсуву дуже швидко знайшли застосування в потокових шифри, так як вони легко реалізовувалися за допомогою цифрової апаратури. У 1965 році Ернст Селмер (Ernst Selmer), головний криптограф норвезького уряду, розробив теорію послідовності регістрів зсуву. Соломон Голомб (Solomon Golomb), математик NSA, написав книгу, показували б деякі свої результати і результати Селмер. Найпростішим видом регістразсуву зі зворотним зв'язком є \u200b\u200bрегістр зсуву з лінійним зворотним зв'язком (linear feedback shift register, далі LFSR або РгСсЛОС). Зворотній зв'язок таких регістрів є просто XOR (додавання по модулю два) деяких бітів регістра, перелік цих бітів називається відвідної послідовністю (tap sequence). Іноді такий регістр називається конфігурацією Фіббоначі. Через простоту послідовності зворотного зв'язку для аналізу РгСсЛОС можна використовувати досить розвинену математичну теорію. Проаналізувавши отримані вихідні послідовності, можна переконатися в тому, що ці послідовності досить випадкові, щоб бути безпечними. РгСсЛОС частіше за інших зсувних регістрів використовуються в криптографії.

Малюнок 2. РгСсЛОС Фіббоначі
У загальному випадку n-бітовий РгСсЛОС може перебувати в одному з N \u003d 2 n -1 внутрішніх станів. Це означає, що теоретично такий регістр може генерувати псевдослучайную послідовність з періодом Т \u003d 2 n -1 бітів. (Число внутрішніх станів і період рівні N \u003d T max \u003d 2 n -1, тому що заповнення РгСсЛОС нулями, призведе до того, що зсувний регістр видаватиме нескінченну послідовність нулів, що абсолютно марно). Тільки за певних відвідних послідовності РгСсЛОС циклічно пройде через всі 2 n -1 внутрішніх станів, такі РгСсЛОС є РгСсЛОС з максимальним періодом. Одержаний результат називається М-послідовністю.
приклад . На малюнку нижче показаний 4-бітовий РгСсЛОС з відведенням від першого і четвертого бітів. Якщо його проинициализировать значенням 1111, то до повторення регістр буде приймати такі внутрішні стану:
 Номер такту зсуву (внутрішнього стану) |
стан регістрів |
вихідний біт |
|||
|
ініціальні значення |
|||||
|
15 (повернення в ініціальні стан) |
|||||
|
16 (повтор станів) |
Вихідний послідовністю буде рядок молодших значущих бітів: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 з періодом Т \u003d 15, загальна кількість можливих внутрішніх станів (крім нульового), N \u003d 2 4 -1 \u003d 16-1 \u003d 15 \u003d T max, отже, вихідна послідовність - M-послідовність.
Для того щоб конкретний РгСсЛОС мав максимальний період, многочлен, утворений з відвідної послідовності і константи 1, повинен бути примітивним по модулю 2. Многочлен представляється у вигляді суми ступенів, наприклад многочлен ступеня n представляється так:
a n x n + a n-1 x n-1 + ... + a 1 x 1 + a 0 x 0 \u003d a n x n + a n-1 x n-1 + ... + a 1 x + a 0 , Де а i \u003d (0,1) для i \u003d 1 ... n, a x i - вказує розряд.
Ступінь многочлена є довжиною зсувного регістру. Примітивний многочлен ступеня n - це не приводиться многочлен, який є дільником x 2n? 1 +1, але не є дільником x d +1 для всіх d, що є дільниками 2 n -1. Відповідну математичну теорію можна знайти в.
У загальному випадку не існує простого способу генерувати примітивні многочлени даної ступеня по модулю 2. Найпростіше вибирати багаточлен випадковим чином і перевіряти, чи не є він примітивним. Це нелегко і чимось схоже на перевірку, чи не є простим випадково вибране число - але багато математичні пакети програм вміють вирішувати таке завдання.
Деякі, але, звичайно ж, не всі, многочлени різних ступенів, примітивні по модулю 2, наведені далі. Наприклад, запис
(32, 7, 5, 3, 2, 1, 0) означає, що наступний многочлен примітивний по модулю 2: x 32 + x 7 + x 5 + x 3 + x 2 + x + 1.
Це можна легко узагальнити для РгСсЛОС з максимальним періодом. Першим числом є довжина РгСсЛОС. Останнє число завжди дорівнює 0, і його можна опустити. Всі числа, за винятком 0, задають відвідну послідовність, відлічувану від лівого краю зсувного регістру. Тобто, члени многочлена з меншим ступенем відповідають позиціям ближче до правого краю регістра.
Продовжуючи приклад, запис (32, 7, 5, 3, 2, 1, 0) означає, що для взятого 32-бітового зсувного регістру новий біт новий біт генерується за допомогою XOR тридцять другого, сьомого, п'ятого, третього, другого і першого бітів , що виходить РгСсЛОС матиме максимальну довжину, циклічно проходячи до повторення через 2 32 -1 значень.

Малюнок 4. 32-бітовий РгСсЛОС з максимальною довжиною
Розглянемо програмний код РгСсЛОС, у якого відвідна послідовність характеризується многочленом (32, 7, 5, 3, 2, 1, 0). Мовою C виглядає наступним чином:
static unsigned long ShiftRegister \u003d 1;
/ * Всі, крім 0. * /
ShiftRegister \u003d ((((ShiftRegister \u003e\u003e 31)
^ (ShiftRegister \u003e\u003e 6)
^ (ShiftRegister \u003e\u003e 4)
^ (ShiftRegister \u003e\u003e 2)
^ (ShiftRegister \u003e\u003e 1)
^ ShiftRegister))
| (ShiftRegister \u003e\u003e 1);
return ShiftRegister & 0x00000001;)
Якщо зсувний регістр довше комп'ютерного слова, код ускладнюється, але не набагато. У додатку B наведена таблиця деяких примітивних многочленів по модулю 2, будемо використовувати її в подальшому для виявлення деяких властивостей цих многочленів, а також в програмній реалізації для завдання відвідної послідовності.
Слід звернути увагу, що у всіх елементів таблиці непарне число коефіцієнтів. Така довга таблиця наведена для подальшої роботи з РгСсЛОС, так як РгСсЛОС часто використовуються для криптографії з потоковими шифрами і в генераторах псевдовипадкових чисел. У нашому випадку можна використовувати многочлени зі старшою ступенем не більше семи.
Якщо p (x) примітивний, то примітивний і x n p (1 / x), тому кожен елемент таблиці насправді визначає два примітивних многочлена. Наприклад, якщо (a, b, 0) примітивний, то примітивний і (a, a-b, 0). Якщо примітивний (a, b, c, d, 0), то примітивний і (a, a-d, a-c, a-b, 0). математично:
якщо примітивний x a + x b +1, то примітивний і x a + x a-b +1,
якщо примітивний x a + x b + x c + x d +1, то примітивний і x a + x a-d + x a-c + x a-b +1. Швидше за все програмно реалізуються примітивні Трехчлен, так як для генерації нового біта потрібно виконувати XOR тільки двох бітів зсувного регістру (нульовий член не враховується, тобто х 0 \u003d 1, см. Приклад вище). Дійсно, всі многочлени зворотного зв'язку, наведені в таблиці, є розрідженими, тобто, у них трохи коефіцієнтів. Розрідженість завжди є джерело слабкості, якої іноді досить для розтину алгоритму. Для криптографічних алгоритмів набагато краще використовувати щільні примітивні многочлени, ті, у яких багато коефіцієнтів. Застосовуючи щільні многочлени, особливо в якості частини ключа, можна використовувати значно коротші РгСсЛОС.
Генерувати щільні примітивні многочлени по модулю 2 нелегко. У загальному випадку для генерації примітивних многочленів ступеня k потрібно знати розкладання на множники числа 2 k -1.
Самі по собі РгСсЛОС є хорошими генераторами псевдовипадкових послідовностей, але вони мають деякі небажаними невипадковими (детермінованими) властивостями. Послідовні біти лінійні, що робить їх марними для шифрування. Для РгСсЛОС довжини n внутрішній стан являє собою попередні n вихідних бітів генератора. Навіть якщо схема зворотного зв'язку зберігається в секреті, вона може бути визначена по 2n вихідних бітів генератора за допомогою високо ефективного алгоритму Berlekamp-Massey.
Крім того, великі випадкові числа, що генеруються з використанням йдуть підряд бітів цієї послідовності, сильно корельовані і для деяких типів додатків зовсім не є випадковими. Незважаючи на це РгСсЛОС часто використовуються для створення алгоритмів шифрування в якості складових частин систем та алгоритмів шифрування.
Найпростішим видом функції зворотного зв'язку є лінійна функція, наприклад, сума по модулю 2 вмісту певних розрядів. Такий регістр називається зсувними регістром з лінійної зворотним зв'язком (Linear Feedback Shift Register, скорочено LFSR). У загальному випадку лінійна функція зворотного зв'язку задається формулою. тут c k\u003d 1, якщо k-й розряд використовується в функції зворотного зв'язку, і c k\u003d 0 в іншому випадку. Символ Å позначає складання по модулю 2 (виключає АБО).
Для прикладу розглянемо LFSR з функцією зворотного зв'язку (див. Малюнок).
Якщо початковим станом регістра є 1111, то в наступних тактах він буде приймати наступний ряд станів: 1111, 0111, 1011, 0101, 1010, 1101, 0110, 0011, 1001, 0100, 0010, 0001, 1000, 1100, 1110, 1111, ...
Вихідна послідовність формується з молодшого (крайнього правого) розряду регістра. Вона буде виглядати наступним чином: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 1. Видно, що генерується бітова послідовність цілком визначається початковим станом регістра і функцією зворотного зв'язку. Оскільки число всіляких станів регістра звичайно (воно дорівнює 2 L), То, рано чи пізно, ключова послідовність почне повторюватися. Максимальна довжина є повторюваною частини ключовий послідовності називається її періодом T. Період залежить від функції зворотного зв'язку. Максимально можливий період дорівнює T max \u003d 2 L-1 (реєстр вживає всіх можливих стану, крім 0000 ... 0). Вихідна послідовність LFSR, що володіє максимальним періодом, називається М-послідовністю.
Щоб з'ясувати умови, при яких LFSR буде володіти максимальним періодом, функції зворотного зв'язку ставлять у відповідність характеристичний поліном. Так, регістру, наведеним вище як приклад, відповідає поліном. Теоретичний аналіз показує, що LFSR буде володіти максимальним періодом тоді і тільки тоді, коли поліном P(x) є примітивним. Нижче наведені деякі примітивні поліноми, рекомендовані до застосування на практиці. У таблиці вказані ступеня змінної xв запису полінома. Наприклад, запис (31, 3) відповідає полиному.
| № | P(x) | № | P(x) | № | P(x) |
| (39, 16, 23, 35) | (38, 5, 6, 27) | (32, 2, 7, 16) | |||
| (30, 6, 4, 1) | (31, 6) | (31, 7) | |||
| (31, 13) | (31, 25, 23, 8) | (33, 13) | |||
| (35, 2) | (47, 5) | (48, 9, 7, 4) | |||
| (47, 11, 24, 32) | (46, 18, 31, 40) | (53, 6, 2, 1) | |||
| (55, 24) | (57, 7) | (58, 19) | |||
| (59, 7, 4, 2) | (41, 27, 31, 32) | (61, 5, 2, 1) | |||
| (42, 30, 31, 34) | (51, 15, 24, 46) | (50, 17, 31, 34) |
Спочатку LFSR були розроблені для апаратної реалізації у вигляді набору цифрових схем. Програмні реалізації LFSR зазвичай програють по швидкості апаратним. Для збільшення швидкодії стан регістра вигідно зберігати в вигляді цілого L-розрядним числа, окремі біти якого відповідають двійковим розрядам регістра. Тоді для доступу до окремих бітам використовуються порозрядні операції (зрушення, маскування і т.д.).
Зсувний регістр зі зворотним зв'язком ( FSR ) складається з двох частин: зсувного регістру і функції зворотного зв'язку .
Зсувний регістр (Error: Reference source not found) являє собою послідовність бітів. Коли потрібно витягти біт, все біти зсувного регістру зсуваються вправо на 1 позицію. Новий крайній лівий біт є значенням функції зворотного зв'язку від інших бітів регістра. періодом зсувного регістру називається довжина одержуваної послідовності до початку її повторення.
Найпростішим видом зсувного регістру зі зворотним зв'язком є лінійний зсувний регістр зі зворотним зв'язком (LFSR
–
Left
Feedback
Shift
Register)
(Error: Reference source not found). Зворотній зв'язок є простоXORнекоторих бітів р  егістра, перелік цих бітів називається відвідної послідовністю.
егістра, перелік цих бітів називається відвідної послідовністю.
n-бітовийLFSRможет перебувати в одному з 2 n -1 внутрішніх станів. Це означає, що теоретично такий регістр може генерувати псевдослучайную послідовність з періодом 2 n -1 бітів. Число внутрішніх станів і період рівні, тому що заповнення регістра нулями призведе до того, що він буде видавати нескінченну послідовність нулів, що абсолютно марно. Тільки за певних відвідних последовательностяхLFSRцікліческі пройде через всі 2 n -1 внутрішніх станів. ТакіеLFSRназиваются LFSR з максимальним періодом.
Для того щоб конкретний LFSRімел максимальний період, многочлен, утворений з відвідної послідовності і константи 1 повинен бути примітивним по модулю 2 .
Обчислення примітивності многочлена - досить складна математична задача. Тому існують готові таблиці, в яких наведені номери відвідних послідовностей, які забезпечують максимальний період генератора. Наприклад, для 32-х бітового зсувного регістру можна знайти такий запис: (32,7,5,3,2,1,0) . Це означає, що для генерації нового біта необхідно за допомогою функцііXORпросумміровать тридцять другому, сьомий, п'ятий, третій, другий, і перший біти.
Код для такого LFSRна мовою С ++ буде таким:
// Будь-яке значення крім нуля
ShiftRegister \u003d ((((ShiftRegister \u003e\u003e 31)
^ (ShiftRegister \u003e\u003e 6)
^ (ShiftRegister \u003e\u003e 4)
^ (ShiftRegister \u003e\u003e 2)
^ (ShiftRegister \u003e\u003e 1)
^ ShiftRegister)
& 0x00000001)<<31)
| (ShiftRegister \u003e\u003e 1);
return ShiftRegister & 0x00000001;
Програмні реалізації LFSRдостаточно повільні і швидше працюють, якщо вони написані на асемблері, а не на С. Одним з рішень є використання паралельно 16-тіLFSR (або 32 в залежності від довжини слова в архітектурі конкретного комп'ютера). У такій схемі використовується масив слів, розмір якого дорівнює длінеLFSR, а кожен ЮІТ слова масиву відноситься до своемуLFSR. За умови, що використовуються однакові номери відвідних послідовностей, то це може дати помітний виграш в продуктивності.
З  хему зворотного зв'язку також можна модифікувати. При цьому генератор не володітиме більшою криптостійкості, але його буде легше реалізувати програмно. Замість використання для генерації нового крайнього лівого біта бітів відвідної послідовності виполняетсяXORкаждого біта відвідної послідовності з виходом генератора і заміна його результатом цієї дії, потім результат генератора стає новим лівим крайнім бітом (Error: Reference source not found).
хему зворотного зв'язку також можна модифікувати. При цьому генератор не володітиме більшою криптостійкості, але його буде легше реалізувати програмно. Замість використання для генерації нового крайнього лівого біта бітів відвідної послідовності виполняетсяXORкаждого біта відвідної послідовності з виходом генератора і заміна його результатом цієї дії, потім результат генератора стає новим лівим крайнім бітом (Error: Reference source not found).
Цю модифікацію називають конфігурацією Галуа. Мовою С це виглядає наступним чином:
static unsigned long ShiftRegister \u003d 1;
void seed_LFSR (unsigned long seed)
ShiftRegister \u003d seed;
int Galua_LFSR (void)
if (ShiftRegister & 0x00000001) (
ShiftRegister \u003d (ShiftRegister ^ mask \u003e\u003e 1) | 0x8000000;
ShiftRegister \u003e\u003e \u003d 1;
Виграш полягає тому, що все XORвиполняются за одну операцію. Ця схема також може бути распараллелена.
Самі по собі LFSRявляются хорошими генераторами псевдовипадкових послідовностей, але вони мають деякі небажаними невипадковими властивостями. Послідовні біти лінійні, що робить їх марними для шифрування. ДляLFSRдліни nвнутрішній стан являє собою попередні nвихідних бітів генератора. Навіть якщо схема зворотного зв'язку зберігається в секреті, то вона може бути визначена по 2 nвихідним бітам генератора за допомогою спеціальних алгоритмів. Крім того, великі випадкові числа, що генеруються з використанням йдуть підряд бітів цієї послідовності, сильно корельовані і для деяких типів додатків не є випадковими. Незважаючи на це, LFSRчасто використовуються для створення алгоритмів шифрування. Для цього використовуються несколькоLFSR, зазвичай з різними довжинами і номерами відвідних послідовностей. Ключ є початковим станом регістрів. Кожен раз, коли необхідний новий біт, все регістри зсуваються. Ця операція називається тактуванням. Біт виходу являє собою функцію, бажано нелінійну, деяких бітовLFSR. Ця функція називається комбінує, А генератор в цілому - комбінує генератором. Багато з таких генераторів безпечні досі.
Регістр зсуву з лінійної зворотним зв'язком (РСЛОС, англ. linear feedback shift register, LFSR) - регістр зсуву бітових слів, у якого значення вхідного (всувають) біта одно лінійної булевої функції від значень інших бітів регістра до зсуву. Може бути організований як програмними, так і апаратними засобами. Застосовується для генерації псевдовипадкових послідовностей бітів, що знаходить застосування, зокрема, в криптографії.
опис
Управління регістром в апаратних реалізаціях здійснюється шляхом здачі сдвигающего імпульсу (інакше званого тактовим або синхроимпульсом) На всі осередки. Управління регістром в програмних реалізаціях проводиться виконанням циклу. На кожній ітерації циклу обчислюється функція зворотного зв'язку і виконується зрушення бітів в слові.
Принцип роботи
лінійна складність
кореляційний незалежність
Намагаючись отримати високу лінійну складність генерується послідовності, криптографи нелінійно об'єднують виходи декількох регістрів зсуву. При цьому одна або кілька вихідних послідовностей (або навіть виходи окремих РСЛОС) можуть бути пов'язані спільним потоком і розкриті криптоаналітиків. Злом на основі такої вразливості називають кореляційним розкриттям. Основна ідея такого злому полягає в виявленні певної кореляції між висновком генератора і висновками його складових частин. Потім, спостерігаючи вихідну послідовність, можна отримати інформацію про ці проміжні висновки, і, таким чином, зламати генератор. Томас Сігенталер показав, що можна точно визначити кореляційну незалежність, і що існує компроміс між кореляційної незалежністю і лінійної складністю.
програмна реалізація
Програмні реалізації РСЛОС досить повільні і працюють швидше, якщо вони написані на асемблері. Одне з рішень - паралельне використання 16-ти РСЛОС (або 32-х, в залежності від довжини слова в архітектурі комп'ютера). У такій схемі використовується масив слів, розмір якого дорівнює довжині регістразсуву, а кожен біт слова ставиться до свого РСЛОС. Так як використовуються однакові номери відвідних послідовностей, то це може дати помітний виграш в продуктивності генератора.
конфігурація Фібоначчі
Розглянемо 32-бітовий зсувний регістр. Для нього є відвідна послідовність (32, 31, 30, 28, 26, 1) (\\ displaystyle \\ left (32, \\; 31, \\; 30, \\; 28, \\; 26, \\; 1 \\ right)). Це означає, що для генерації нового біта необхідно за допомогою операції XOR підсумувати 31-й, 30-й, 29-й, 27-й, 25-й і 0-й біти. Отриманий РСЛОС має максимальний період 2 32 - 1 (\\ displaystyle 2 ^ (32) -1). Код для такого регістра на мові Сі наступний:
int LFSR_Fibonacci (void) (static unsigned long S \u003d 0x00000001; S \u003d ((((S \u003e\u003e 31) ^ (S \u003e\u003e 30) ^ (S \u003e\u003e 29) ^ (S \u003e\u003e 27) ^ (S \u003e\u003e 25) ^ S) & 0x00000001)<< 31 ) | (S >\u003e 1); return S & 0x00000001; )
конфігурація Галуа
Даний генератор не володіє більшою криптостійкості, але він дає виграш в продуктивності: все операції XOR за допомогою розпаралелювання можна виконати за одну дію, а не послідовно одна за одною, як у конфігурації Фібоначчі. Дана схема також дасть виграш при апаратній реалізації.
Код для регістразсуву довжини 32 біт на мові Сі наступний:
int LFSR_Galois (void) (static unsigned long S \u003d 0x00000001; if (S & 0x00000001) (S \u003d (S ^ 0x80000057 \u003e\u003e 1) | 0x80000000; return 1;) else (S \u003e\u003e \u003d 1; return 0;))
Варто відзначити, що цикл з фіксованого числа викликів функції LFSR_Galois в конфігурації Галуа виконується приблизно в 2 рази швидше, ніж функція LFSR_Fibonacci в конфігурації Фібоначчі (компілятор MS VS 2010 року на Intel Core i5).
Приклад генерується послідовності
конфігурація Фібоначчі
Нехай РСЛОС задається характеристичним многочленом x 3 + x + 1 (\\ displaystyle x ^ (3) + x + 1). Це означає, що битами відведення будуть 2-й і 0-й, а одиниця у формулі многочлена означає, що 0-й біт - вхідний. Функція зворотного зв'язку має вигляд S j \u003d S j - 1 ⊕ S j - 3 (\\ displaystyle S_ (j) \u003d S_ (j-1) \\ oplus S_ (j-3)). Припустимо, початковим станом регістразсуву була послідовність. Подальші стану регістра наведено в таблиці нижче:
| номер кроку | стан | генерується біт |
|---|---|---|
| 0 | [0, 0, 1] (\\ displaystyle \\ left) | 1 |
| 1 | 0 | |
| 2 | 0 | |
| 3 | 1 | |
| 4 | 1 | |
| 5 | 1 | |
| 6 | 0 | |
| 7 | [0, 0, 1] (\\ displaystyle \\ left) | 1 |
Оскільки внутрішній стан на сьомому кроці повернулося до вихідного, то, починаючи з наступного кроку, буде йти повтор бітів. Тобто генерується послідовність така: [1, 0, 0, 1, 1, 1, 0, 1. . . ] (\\ Displaystyle \\ left) (Порядок біт в послідовності відповідає порядку їх генерації РСЛОС). Таким чином, період послідовності дорівнює 7, тобто максимально можливого значення, що відбулося в силу примітивності заданого многочлена.
конфігурація Галуа
Візьмемо той же характеристичний многочлен, тобто c 3 \u003d c 1 \u003d 1 (\\ displaystyle c_ (3) \u003d c_ (1) \u003d 1), c 2 \u003d 0 (\\ displaystyle c_ (2) \u003d 0). З вихідним бітом складається тільки 1-й біт. Початковий стан те ж саме. Подальші стану регістра:
| номер кроку | стан | генерується біт |
|---|---|---|
| 0 | [0, 0, 1] (\\ displaystyle \\ left) | - |
| 1 | [1, 0, 0] (\\ displaystyle \\ left) | 0 |
| 2 | [0, 1, 1] (\\ displaystyle \\ left) | 1 |
| 3 | [1, 0, 1] (\\ displaystyle \\ left) | 1 |
| 4 | [1, 1, 1] (\\ displaystyle \\ left) | 1 |
| 5 | [1, 1, 0] (\\ displaystyle \\ left) | 0 |
| 6 | [0, 1, 0] (\\ displaystyle \\ left) | 0 |
| 7 | [0, 0, 1] (\\ displaystyle \\ left) | 1 |
Внутрішній стан регістра на сьомому кроці повернулося до вихідного, отже, його період також дорівнює 7. На відміну від конфігурації Фібоначчі, внутрішні стану регістра вийшли інші, але що генерується послідовність та ж, тільки зрушена на 4 такти: [0, 1, 1, 1, 0, 0, 0, 0, 1, 1,. . . ] (\\ Displaystyle \\ left) (Порядок біт в послідовності відповідає порядку їх генерації РСЛОС).
Генерація примітивних многочленів
| біти, n (\\ displaystyle n) | примітивний многочлен | період, 2 n - 1 (\\ displaystyle 2 ^ (n) -1) | Число примітивних многочленів |
|---|---|---|---|
| 2 | x 2 + x + 1 (\\ displaystyle x ^ (2) + x + 1) | 3 | 1 |
| 3 | x 3 + x 2 + 1 (\\ displaystyle x ^ (3) + x ^ (2) +1) | 7 | 2 |
| 4 | x 4 + x 3 + 1 (\\ displaystyle x ^ (4) + x ^ (3) +1) | 15 | 2 |
| 5 | x 5 + x 3 + 1 (\\ displaystyle x ^ (5) + x ^ (3) +1) | 31 | 6 |
| 6 | x 6 + x 5 + 1 (\\ displaystyle x ^ (6) + x ^ (5) +1) | 63 | 6 |
| 7 | x 7 + x 6 + 1 (\\ displaystyle x ^ (7) + x ^ (6) +1) | 127 | 18 |
| 8 | x 8 + x 6 + x 5 + x 4 + 1 (\\ displaystyle x ^ (8) + x ^ (6) + x ^ (5) + x ^ (4) +1) | 255 | 16 |
| 9 | x 9 + x 5 + 1 (\\ displaystyle x ^ (9) + x ^ (5) +1) | 511 | 48 |
| 10 | x 10 + x 7 + 1 (\\ displaystyle x ^ (10) + x ^ (7) +1) | 1023 | 60 |
| 11 | x 11 + x 9 + 1 (\\ displaystyle x ^ (11) + x ^ (9) +1) | 2047 | 176 |
| 12 | x 12 + x 11 + x 10 + x 4 + 1 (\\ displaystyle x ^ (12) + x ^ (11) + x ^ (10) + x ^ (4) +1) | 4095 | 144 |
| 13 | x 13 + x 12 + x 11 + x 8 + 1 (\\ displaystyle x ^ (13) + x ^ (12) + x ^ (11) + x ^ (8) +1) | 8191 | 630 |
| 14 | x 14 + x 13 + x 12 + x 2 + 1 (\\ displaystyle x ^ (14) + x ^ (13) + x ^ (12) + x ^ (2) +1) | 16383 | 756 |
| 15 | x 15 + x 14 + 1 (\\ displaystyle x ^ (15) + x ^ (14) +1) | 32767 | 1800 |
| 16 | x 16 + x 14 + x 13 + x 11 + 1 (\\ displaystyle x ^ (16) + x ^ (14) + x ^ (13) + x ^ (11) +1) | 65535 | 2048 |
| 17 | x 17 + x 14 + 1 (\\ displaystyle x ^ (17) + x ^ (14) +1) | 131071 | 7710 |
| 18 | x 18 + x 11 + 1 (\\ displaystyle x ^ (18) + x ^ (11) +1) | 262143 | 7776 |
| 19 | x 19 + x 18 + x 17 + x 14 + 1 (\\ displaystyle x ^ (19) + x ^ (18) + x ^ (17) + x ^ (14) +1) | 524287 | 27594 |
| 20 - 168 | |||
| 2 - 786, 1024, 2048, 4096 | |||
Переваги і недоліки
переваги
- високу швидкодію криптографічних алгоритмів, що створюються на основі РСЛОС (наприклад потокових шифрів);
- застосування тільки найпростіших бітових операцій додавання і множення, апаратно реалізованих практично у всіх обчислювальних пристроях;
- хороші криптографічні властивості (РСЛОС можуть генерувати послідовності великого періоду з хорошими статистичними властивостями);
- завдяки своїй структурі, РСЛОС легко аналізуються з використанням алгебраїчних методів.
недоліки
Способи поліпшення криптостойкости генеруються послідовностей
Генератори з декількома регістрами зсуву
Генератор такого типу складається з декількох регістрів зсуву з лінійної зворотним зв'язком, які генерують біти x 1, i, x 2, i, ..., x M, i (\\ displaystyle x_ (1, i), \\; x_ (2, i), \\; \\ dots, \\; x_ (M, i)) відповідно. Далі, що генеруються біти перетворюються якоїсь булевої функцією f (x 1, i, x 2, i, ..., x M, i) (\\ displaystyle f (x_ (1, i), \\; x_ (2, i), \\; \\ dots, \\; x_ (M , i))). Необхідно відзначити, що у генераторів такого типу довжини регістрів L i (\\ displaystyle L_ (i)), i \u003d 1, 2, ..., M (\\ displaystyle i \u003d 1, \\; 2, \\; \\ dots, \\; M), Взаємно прості між собою.
Період даного генератора дорівнює T \u003d (2 L 1 - 1) ⋅ (2 L 2 - 1) ⋯ (2 LM - 1) ≲ 2 L (\\ displaystyle T \u003d (2 ^ (L_ (1)) - 1) \\ cdot (2 ^ ( L_ (2)) - 1) \\ cdots (2 ^ (L_ (M)) - 1) \\ lesssim 2 ^ (L)), де L \u003d Σ i \u003d 1 M L i (\\ displaystyle L \u003d \\ sum \\ limits _ (i \u003d 1) ^ (M) L_ (i)) - загальне число осередків. Отже, використання декількох РСЛОС збільшує період генерується послідовності в порівнянні з одним регістром, що збільшує криптостойкость генератора. Також збільшується лінійна складність або довжина найкоротшого регістра, яке відповідає даному генератору. Такий реєстр знаходиться за допомогою алгоритму Берлекемпа - Мессі по генерується послідовності. У кращому випадку його довжина порівнянна з періодом генерується послідовності.
Генератори з нелінійними перетвореннями
Структурна схема такого генератора нічим не відрізняється від схеми попереднього генератора. Головна відмінність полягає в тому, що пристрій перетворення задано нелінійної булевої функцією f (x 1, x 2, ..., x M) (\\ displaystyle f (x_ (1), x_ (2), \\ dots, x_ (M))). В якості такої функції береться, наприклад, поліном Жегалкина (згідно з теоремою Жегалкина, всяка булева функція єдиним чином може бути представлена \u200b\u200bполіномом Жегалкина).
Нелінійний генератор може бути також реалізований на регістрі зсуву з нелінійним зворотним зв'язком. Він може дати 2 2 L - 1 - L (\\ displaystyle 2 ^ (2 ^ (L-1) -L)) варіантів послідовностей максимального періоду, що більше, ніж у РСЛОС.
Крипостійкість даного генератора підвищується за рахунок нелінійності використовуваної функції. Визначення стану регістрів по генерується послідовності бітів є складною математичною задачею, тому що ніхто не знає алгоритм, який відновлює вихідні стану.
Даний метод використовується, наприклад, в генераторі Геффена і узагальненому генераторі Геффена, однак такі генератори можуть бути зламані кореляційним розкриттям.
Генератори з різним тактуванням регістрів зсуву
Генератор «стоп-пішов»
Генератор «стоп-пішов» (Англ. Stop-and-Go, Both-Piper) використовує висновок РСЛОС-1 для управління тактовою частотою РСЛОС-2, так що РСЛОС-2 змінює свій стан в певний момент часу, тільки якщо вихід РСЛОС-1 в момент часу дорівнював одиниці. Дана схема не встояла перед кореляційним розкриттям.
З метою збільшення криптостійкості був запропонований чергується генератор «стоп-пішов». У ньому використовуються три регістру зсуву різної довжини. Тут РСЛОС-1 управляє тактовою частотою 2-го і 3-го регістрів, тобто РСЛОС-2 змінює свій стан, коли вихід РСЛОС-1 дорівнює одиниці, а РСЛОС-3 - коли вихід РСЛОС-1 дорівнює нулю. Виходом генератора є операція додавання по модулю два виходів РСЛОС-2 і РСЛОС-3. У даного генератора великий період і велика лінійна складність. Існує спосіб кореляційного розтину РСЛОС-1, але це не сильно послаблює криптографічні властивості генератора.
Ускладнена схема тактирования використана в двосторонньому генераторі «стоп-пішов», В якому використовуються 2 регістра зсуву однакової довжини. Якщо вихід РСЛОС-1 в певний момент часу t i - 1 (\\ displaystyle t_ (i-1)) - одиниці, то РСЛОС-2 не тактується в момент часу t i (\\ displaystyle t_ (i)). Якщо вихід РСЛОС-2 в момент часу t i - 1 (\\ displaystyle t_ (i-1)) дорівнює нулю, а в момент часу t i - 2 (\\ displaystyle t_ (i-2)) - одиниці, і якщо цей реєстр тактується в момент часу t i (\\ displaystyle t_ (i)), То в цей же момент РСЛОС-1 не тактується. Лінійна складність даної схеми приблизно дорівнює періоду генерується послідовності.
Самопрорежівающій генератор
Багатошвидкісний генератор з внутрішнім твором
Даний генератор використовує два регістри зсуву РСЛОС-1 і РСЛОС-2. Тактова частота РСЛОС-2 в d (\\ displaystyle d) раз більше, ніж у РСЛОС-1. Певні біти цих регістрів перемножуються між собою операцією AND. Результати умножений підсумовуються операцією XOR, і виходить вихідна послідовність. Цей генератор має високу лінійну складність і володіє хорошими статистичними властивостями. Однак його стан може бути визначено по вихідний послідовності довжиною L 1 + L 2 + log 2 \u2061 d (\\ displaystyle L_ (1) + L_ (2) + \\ log _ (2) (d)), де L 1 (\\ displaystyle L_ (1)) і L 2 (\\ displaystyle L_ (2)) - довжини РСЛОС-1 і РСЛОС-2 відповідно, а d (\\ displaystyle d) - ставлення їх тактових частот.
каскад Голлманна
Дана схема являє собою поліпшену версію генератора «стоп-пішов». Він складається з послідовності РСЛОС, тактирование кожного з яких управляється попереднім РСЛОС. Якщо виходом РСЛОС-1 в момент часу t i (\\ displaystyle t_ (i)) є 1, то тактується РСЛОС-2. Якщо виходом РСЛОС-2 в момент часу t i (\\ displaystyle t_ (i)) є 1, то тактується РСЛОС-3, і так далі. Вихід останнього РСЛОС є виходом генератора. Якщо довжина всіх РСЛОС однакова і дорівнює L (\\ displaystyle L), То період системи з M (\\ displaystyle M) РСЛОС дорівнює (2 L - 1) M (\\ displaystyle (2 ^ (L) -1) ^ (M)), А лінійна складність - L (S) \u003d L (2 L - 1) M - 1 (\\ displaystyle L (S) \u003d L (2 ^ (L) -1) ^ (M-1)) .
Ця ідея проста і може бути використана для генерації послідовностей з величезними періодами, більшими лінійними складнощами і хорошими статистичними властивостями. Але, на жаль, вони чутливі до розтину, званому замиканням (Англ. Lock-in), коли
Послідовності зсувних регістрів використовуються як в криптографії, так і в теорії кодування. Їх теорія прекрасно опрацьована, потокові шифри на базі зсувних регістрів були робочою конячкою військової криптографії задовго до появи електроніки.
Зсувний регістр зі зворотним зв'язком складається з двох частин: зсувного регістру і функції зворотного зв'язку (рисунок 1.2.1). Зсувний регістр представляє собою послідовність бітів. (Кількість бітів визначається довжиною зсувного регістру. Якщо довжина дорівнює n бітів, то регістр називається n-бітових зсувними регістром.) Всякий раз, коли потрібно витягти біт, все біти зсувного регістру зсуваються вправо на 1 позицію. Новий крайній лівий біт є функцією всіх інших бітів регістра. На виході зсувного регістру виявляється один, зазвичай молодший значущий, біт. Періодом зсувного регістру називається довжина одержуваної послідовності до початку її повторення.
Мал. 1.2.1.
Криптографії подобалися потокові шифри на базі зсувних регістрів: вони легко реалізовувалися за допомогою цифрової апаратури. Я лише злегка торкнуся математичну теорію. У 1965 році Ернст Селмер (Ernst Selmer), головний криптограф норвезького уряду, розробив теорію послідовності зсувних регістрів. Соломон Голомб (Solomon Golomb), математик NSA, написав книгу, показували б деякі свої результати і результати Селмер.
Найпростішим видом зсувного регістру зі зворотним зв'язком є \u200b\u200bлінійний зсувний регістр зі зворотним зв'язком (linear feedback shift register, або LFSR) (рисунок 1.2.2). Зворотній зв'язок є просто XOR деяких бітів регістра, перелік цих бітів називається відвідної послідовністю (tap sequence). Іноді такий регістр називається конфігурацією Фіббоначі. Через простоту послідовності зворотного зв'язку для аналізу LFSR можна використовувати досить розвинену математичну теорію. Криптографи люблять аналізувати послідовності, переконуючи себе, що ці послідовності досить випадкові, щоб бути безпечними. LFSR частіше за інших зсувних регістрів використовуються в криптографії.

Мал. 1.2.2.
На Рис. 1.2.3 показаний 4-бітовий LFSR з відведенням від першого і четвертого бітів. Якщо його проинициализировать значенням 1111, то до повторення регістр буде приймати такі внутрішні стану:

Мал. 1.2.3. 4
Вихідний послідовністю буде рядок молодших значущих бітів:
1 1 1 1 0 1 0 1 1 0 0 1 0 0 0....
n-бітовий LFSR може перебувати в одному з 2n-1 внутрішніх станів. Це означає, що теоретично такий регістр може генерувати псевдослучайную послідовність з періодом 2n-1 бітів. (Число внутрішніх станів і період рівні 2n-1, тому що заповнення LFSR нулями, призведе до того, що зсувний регістр видаватиме нескінченну послідовність нулів, що абсолютно марно.) Тільки при певних відвідних послідовності LFSR циклічно пройде через всі 2n-1 внутрішніх станів , такі LFSR є LFSR з максимальним періодом. Одержаний результат називається М-послідовністю.
Для того, щоб конкретний LFSR мав максимальний період, многочлен, утворений з відвідної послідовності і константи 1, повинен бути примітивним по модулю 2. Ступінь многочлена є довжиною зсувного регістру. Примітивний многочлен ступеня n - це не приводиться многочлен, який є дільником, але не є дільником xd + 1 для всіх d, що є дільниками 2n-1.
У загальному випадку не існує простого способу генерувати примітивні многочлени даної ступеня по модулю 2. Найпростіше вибирати багаточлен випадковим чином і перевіряти, чи не є він примітивним. Це нелегко - і чимось схоже на перевірку, чи не є простим випадково вибране число - але багато математичні пакети програм вміють вирішувати таке завдання.
Деякі, але, звичайно ж, не всі, многочлени різних ступенів, примітивні по модулю 2. Наприклад, запис (32, 7, 5, 3, 2, 1, 0) означає, що наступний многочлен примітивний по модулю 2:
x32 + x7 + x5 + x3 + x2 + x + 1
Це можна легко узагальнити для LFSR з максимальним періодом. Першим числом є довжина LFSR. Останнє число завжди дорівнює 0, і його можна опустити. Всі числа, за винятком 0, задають відвідну послідовність, відлічувану від лівого краю зсувного регістру. Тобто, члени многочлена з меншим ступенем відповідають позиціям ближче до правого краю регістра.
Продовжуючи приклад, запис (32, 7, 5, 3, 2, 1, 0) означає, що для взятого 32-бітового зсувного регістру новий біт новий біт генерується за допомогою XOR тридцять другого, сьомого, п'ятого, третього, другого і першого бітів виходить LFSR матиме максимальну довжину, циклічно проходячи до повторення через 232-1 значень.
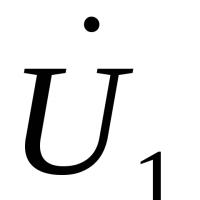 Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок
Магнітометрія У найпростішому варіанті феррозонд складається з феромагнітного сердечника і знаходяться на ньому двох котушок Ефективний пошук роботи Курс з пошуку роботи
Ефективний пошук роботи Курс з пошуку роботи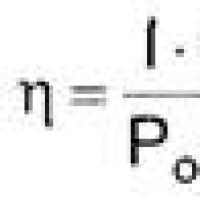 Основні характеристики і параметри фотодіода
Основні характеристики і параметри фотодіода Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF
Як редагувати PDF (п'ять додатків для зміни PDF-файлів) Як виокремити окремі сторінки з PDF Чому згорнуте вікно програми довго розгортається?
Чому згорнуте вікно програми довго розгортається? DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt
DXF2TXT - Експорт та переклад тексту з AutoCAD Вивести точки з автокад dwg в \u200b\u200btxt Що робити якщо пропав курсор миші
Що робити якщо пропав курсор миші