Egy mátrix szorzata online szám alapján. Alapműveletek mátrixokon (összeadás, szorzás, transzponálás) és tulajdonságaik. A mátrix számmal való megszorzásának tulajdonságai
Ez a téma olyan műveletekre terjed ki, mint a mátrixok összeadása és kivonása, a mátrix megszorzása egy számmal, a mátrix szorzása mátrixszal, a mátrix átültetése. Az ezen az oldalon használt összes szimbólum az előző témából származik.
Mátrixok összeadása és kivonása.
A $ A + B $ $ A_ (m \ alkalommal n) = (a_ (ij)) $ és $ B_ (m \ times n) = (b_ (ij)) $ mátrixok összegét $ C_ (m \ times n) = (c_ (ij)) $, ahol $ c_ (ij) = a_ (ij) + b_ (ij) $ minden $ i = \ overline (1, m) $ és $ j = \ overline ( 1, n) $.
Hasonló meghatározást vezetnek be a mátrixok különbségére:
A $ A_ (m \ times n) = (a_ (ij)) $ és $ B_ (m \ times n) = (b_ (ij)) $ mátrix $ AB $ különbsége a $ C_ mátrix (m \ x n ) = (c_ (ij)) $, ahol $ c_ (ij) = a_ (ij) -b_ (ij) $ minden $ i = \ overline (1, m) $ és $ j = \ overline (1, n ) $.
A bejegyzés magyarázata $ i = \ overline (1, m) $: show \ hide
A "$ i = \ overline (1, m) $" jelölés azt jelenti, hogy a $ i $ paraméter 1 -től m -ig terjed. Például a $ i = \ overline (1,5) $ rekord azt mondja, hogy a $ i $ paraméter az 1, 2, 3, 4, 5 értékeket veszi fel.
Meg kell jegyezni, hogy az összeadás és kivonás műveleteket csak azonos méretű mátrixok esetén határozzuk meg. Általában a mátrixok összeadása és kivonása intuitív módon egyértelmű műveletek, mivel valójában csak a megfelelő elemek összeadását vagy kivonását jelentik.
1. példa
Három mátrixot adunk meg:
$$ A = \ bal (\ begin (tömb) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (tömb) \ jobb) \; \; B = \ bal (\ begin (tömb) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (tömb) \ jobb); \; \; F = \ bal (\ begin (tömb) (cc) 1 & 0 \\ -5 & 4 \ end (tömb) \ jobb). $$
Megtalálja a $ A + F $ mátrixot? Keresse meg a $ C $ és $ D $ mátrixokat, ha $ C = A + B $ és $ D = A-B $.
A $ A $ mátrix 2 sort és 3 oszlopot tartalmaz (más szóval a $ A $ mátrix mérete $ 2 \ x 3 $), a $ F $ mátrix pedig 2 sort és 2 oszlopot tartalmaz. A $ A $ és $ F $ mátrix méretei nem esnek egybe, ezért nem adhatjuk hozzá őket, azaz ezeknek a mátrixoknak a $ A + F $ művelete nincs meghatározva.
A $ A $ és $ B $ mátrixok mérete megegyezik, azaz a mátrixadatok egyenlő számú sort és oszlopot tartalmaznak, így az összeadási művelet rájuk is alkalmazható.
$$ C = A + B = \ bal (\ begin (tömb) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (tömb) \ jobb) + \ left (\ begin (tömb ) (ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (tömb) \ jobb) = \\ = \ left (\ begin (array) (ccc) -1 + 10 & -2+ ( -25) & 1 + 98 \\ 5 + 3 & 9 + 0 & -8 + ( -14) \ end (tömb) \ right) = \ left (\ begin (array) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \ end (tömb) \ jobb) $$
Keresse meg a $ D = A-B $ mátrixot:
$$ D = AB = \ left (\ begin (array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \ end (tömb) \ right) -\ left (\ begin (array) { ccc) 10 & -25 & 98 \\ 3 & 0 & -14 \ end (tömb) \ jobb) = \\ = \ left (\ begin (tömb) (ccc) -1-10 & -2 -( -25 ) & 1-98 \\ 5-3 & 9-0 & -8 -( -14) \ end (tömb) \ right) = \ left (\ begin (tömb) (ccc) -11 & 23 & -97 \ \ 2 & 9 & 6 \ end (tömb) \ jobb) $$
Válasz: $ C = \ left (\ begin (tömb) (ccc) 9 & -27 & 99 \\ 8 & 9 & -22 \ end (tömb) \ right) $, $ D = \ left (\ begin (tömb) (ccc) -11 & 23 & -97 \\ 2 & 9 & 6 \ end (tömb) \ right) $.
Egy mátrix szorzása egy számmal.
A $ A_ (m \ times n) = (a_ (ij)) $ mátrix $ $ alpha szorzata a $ B_ (m \ times n) = (b_ (ij)) $ mátrix, ahol $ b_ (ij) = \ alpha \ cdot a_ (ij) $ minden $ i = \ overline (1, m) $ és $ j = \ overline (1, n) $ esetén.
Egyszerűen fogalmazva, a mátrix megszorzása egy bizonyos számmal azt jelenti, hogy egy adott mátrix minden elemét megszorozzuk ezzel a számmal.
2. példa
A mátrix a következő: $ A = \ left (\ begin (tömb) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (tömb) \ right) $. Keresse meg a $ 3 \ cdot A $, $ -5 \ cdot A $ és $ -A $ mátrixokat.
$$ 3 \ cdot A = 3 \ cdot \ left (\ begin (tömb) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (tömb) \ right) = \ left (\ begin ( tömb) (ccc) 3 \ cdot (-1) & 3 \ cdot (-2) & 3 \ cdot 7 \\ 3 \ cdot 4 & 3 \ cdot 9 & 3 \ cdot 0 \ end (tömb) \ right) = \ left (\ begin (tömb) (ccc) -3 & -6 & 21 \\ 12 & 27 & 0 \ end (tömb) \ right). \\ -5 \ cdot A = -5 \ cdot \ left (\ begin (tömb) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (tömb) \ right) = \ left (\ begin (array) (ccc) -5 \ cdot (-1) & -5 \ cdot (-2) & -5 \ cdot 7 \\ -5 \ cdot 4 & -5 \ cdot 9 & -5 \ cdot 0 \ end (tömb) \ jobb) = \ left (\ begin (tömb) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \ end (tömb) \ jobb). $$
A $ -A $ jelölés a $ -1 \ cdot A $ rövidítése. Vagyis a $ -A $ megtalálásához meg kell szorozni a $ A $ mátrix összes elemét (-1) -vel. Valójában ez azt jelenti, hogy a $ A $ mátrix minden elemének jele az ellenkezőjére változik:
$$ -A = -1 \ cdot A = -1 \ cdot \ left (\ begin (tömb) (ccc) -1 & -2 & 7 \\ 4 & 9 & 0 \ end (tömb) \ right) = \ bal (\ begin (tömb) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \ end (tömb) \ jobb) $$
Válasz: $ 3 \ cdot A = \ left (\ begin (tömb) (ccc) -3 & -6 & 21 \\ 12 & 27 & 0 \ end (tömb) \ jobb); \; -5 \ cdot A = \ left (\ begin (tömb) (ccc) 5 & 10 & -35 \\ -20 & -45 & 0 \ end (tömb) \ jobb); \; -A = \ bal (\ begin (tömb) (ccc) 1 & 2 & -7 \\ -4 & -9 & 0 \ end (tömb) \ jobb) $.
Két mátrix szorzata.
Ennek a műveletnek a meghatározása nehézkes, és első pillantásra érthetetlen. Ezért először egy általános definíciót jelzek, majd részletesen elemezzük, mit jelent és hogyan kell vele dolgozni.
A $ C_ (m \ alkalommal k) = (c_ (ij)) $ mátrix, amelyre a $ c_ (ij) $ minden eleme megegyezik az i. Sorának megfelelő elemeinek szorzatával $ A $ mátrix a $ B $ mátrix j-edik oszlopának elemeivel: $$ c_ (ij) = \ összeg \ korlátok_ (p = 1) ^ (n) a_ (ip) b_ (pj), \ ; \; i = \ overline (1, m), j = \ overline (1, n). $$
Elemezzük lépésről lépésre a mátrixszorzást egy példa segítségével. Azonban azonnal figyelnie kell arra a tényre, hogy nem minden mátrixot lehet megszorozni. Ha meg akarjuk szorozni a $ A $ mátrixot a $ B $ mátrixszal, akkor először meg kell győződnünk arról, hogy a $ A $ mátrix oszlopainak száma megegyezik a $ B $ mátrix sorainak számával (ilyen a mátrixokat gyakran nevezik egyetért). Például a $ A_ (5 \ x 4) $ mátrix (a mátrix 5 sort és 4 oszlopot tartalmaz) nem szorozható meg a $ F_ (9 \ x 8) $ (9 sor és 8 oszlop) mátrixszal, mivel a szám $ A $ mátrix oszlopainak száma nem egyenlő a $ F $ mátrix sorainak számával, azaz 4 dollár = 9 dollár. De megszorozhatja a $ A_ (5 \ x 4) $ mátrixot a $ B_ (4 \ x 9) $ mátrixszal, mivel a $ A $ mátrix oszlopainak száma megegyezik a $ mátrix sorainak számával B $. Ebben az esetben a $ A_ (5 \ x 4) $ és $ B_ (4 \ x 9) $ mátrixok megszorzásának eredménye a $ C_ (5 \ 9 9) $ mátrix lesz, amely 5 sort és 9 oszlopot tartalmaz:
3. példa
A mátrixok a következők: $ A = \ left (\ begin (array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & -5 \ end (tömb) \ jobb) $ és $ B = \ left (\ begin (array) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \ end (tömb) \ igaz) $. Keresse meg a $ C = A \ cdot B $ mátrixot.
Először is határozzuk meg azonnal a $ C $ mátrix méretét. Mivel $ A $ $ 3 \ x 4 $ és $ B $ $ 4 \ x 2 $, a $ C $ mérete $ 3 \ x 2 $:

Tehát a $ A $ és $ B $ mátrixok szorzatának eredményeként meg kell kapnunk a $ C $ mátrixot, amely három sorból és két oszlopból áll: $ C = \ left (\ begin (array) (cc) c_ (11) & c_ (12) \\ c_ (21) & c_ (22) \\ c_ (31) & c_ (32) \ end (tömb) \ jobb) $. Ha az elemek megjelölései kérdéseket vetnek fel, akkor megnézheti az előző témát: "Mátrixok. Mátrixok típusai. Alapfogalmak", amelynek elején a mátrixelemek megnevezését ismertetjük. Célunk, hogy megtaláljuk a $ C $ mátrix összes elemének értékeit.
Kezdjük a $ c_ (11) $ összeggel. A $ c_ (11) $ elem megszerzéséhez meg kell találnia a $ A $ mátrix első sora és a $ B $ mátrix első oszlopának elemeinek szorzatát:

Ahhoz, hogy megtalálja magát a $ c_ (11) $ elemet, meg kell szoroznia a $ A $ mátrix első sorának elemeit a $ B $ mátrix első oszlopának megfelelő elemeivel, azaz az első elem az első, a második a második, a harmadik a harmadik, a negyedik a negyedik. Összefoglaljuk a kapott eredményeket:
$$ c_ (11) =- 1 \ cdot (-9) +2 \ cdot 6 + (- 3) \ cdot 7 + 0 \ cdot 12 = 0. $$
Folytassuk a megoldást, és keressük meg a $ c_ (12) $ -t. Ehhez meg kell szorozni a $ A $ mátrix első sorának és a $ B $ mátrix második oszlopának elemeit:

Az előzőhöz hasonlóan nálunk:
$$ c_ (12) =- 1 \ cdot 3 + 2 \ cdot 20 + (- 3) \ cdot 0 + 0 \ cdot (-4) = 37. $$
A $ C $ első sorának minden eleme megtalálható. Lépjen a második sorba, amely $ c_ (21) $ karakterrel kezdődik. Ennek megtalálásához meg kell szorozni a $ A $ mátrix második sorának és a $ B $ mátrix első oszlopának elemeit:

$$ c_ (21) = 5 \ cdot (-9) +4 \ cdot 6 + (-2) \ cdot 7 + 1 \ cdot 12 = -23. $$
A következő $ c_ (22) $ elemet úgy találjuk meg, hogy megszorozzuk a $ A $ mátrix második sorának elemeit a $ B $ mátrix második oszlopának megfelelő elemeivel:
$$ c_ (22) = 5 \ cdot 3 + 4 \ cdot 20 + (- 2) \ cdot 0 + 1 \ cdot (-4) = 91. $$
A $ c_ (31) $ megtalálásához megszorozzuk a $ A $ mátrix harmadik sorának elemeit a $ B $ mátrix első oszlopának elemeivel:
$$ c_ (31) =- 8 \ cdot (-9) +11 \ cdot 6 + (- 10) \ cdot 7 + (-5) \ cdot 12 = 8. $$
És végül, hogy megtalálja a $ c_ (32) $ elemet, meg kell szoroznia a $ A $ mátrix harmadik sorának elemeit a $ B $ mátrix második oszlopának megfelelő elemeivel:
$$ c_ (32) =- 8 \ cdot 3 + 11 \ cdot 20 + (- 10) \ cdot 0 + (-5) \ cdot (-4) = 216. $$
A $ C $ mátrix összes eleme megtalálható, csak annyit kell írni, hogy $ C = \ left (\ begin (array) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (array) ) \ ugye) $ ... Vagy, hogy teljes egészében leírjam:
$$ C = A \ cdot B = \ left (\ begin (tömb) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\ -8 & 11 & -10 & - 5 \ end (tömb) \ jobb) \ cdot \ left (\ begin (tömb) (cc) -9 & 3 \\ 6 & 20 \\ 7 & 0 \\ 12 & -4 \ end (tömb) \ jobb) = \ bal (\ begin (tömb) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (tömb) \ jobb). $$
Válasz: $ C = \ left (\ begin (tömb) (cc) 0 & 37 \\ -23 & 91 \\ 8 & 216 \ end (tömb) \ right) $.
Egyébként gyakran nincs okuk részletesen leírni az eredménymátrix egyes elemeinek megállapítását. A kicsi méretű mátrixok esetében a következőket teheti:
$$ \ left (\ begin (array) (cc) 6 & 3 \\ -17 & -2 \ end (array) \ right) \ cdot \ left (\ begin (array) (cc) 4 & 9 \\ - 6 & 90 \ end (tömb) \ jobb) = \ left (\ begin (array) (cc) 6 \ cdot (4) +3 \ cdot (-6) & 6 \ cdot (9) +3 \ cdot (90 ) \\ -17 \ cdot (4) + (-2) \ cdot (-6) & -17 \ cdot (9) + (-2) \ cdot (90) \ end (tömb) \ right) = \ left (\ begin (tömb) (cc) 6 & 324 \\ -56 & -333 \ end (tömb) \ right) $$
Azt is érdemes megjegyezni, hogy a mátrixszorzás nem kommutatív. Ez azt jelenti, hogy általában $ A \ cdot B \ neq B \ cdot A $. Csak bizonyos típusú mátrixokhoz, amelyeket ún permutáció(vagy ingázás), a $ A \ cdot B = B \ cdot A $ egyenlőség igaz. Pontosan a szorzás nem kommutativitása alapján pontosan meg kell jelölni, hogyan szorozzuk meg a kifejezést ezzel vagy azzal a mátrixszal: jobbra vagy balra. Például a "szorozza meg a $ 3E-F = Y $ egyenlőség mindkét oldalát a jobb oldali $ A $ mátrix" kifejezés azt jelenti, hogy meg kell szereznünk a következő egyenlőséget: $ (3E-F) \ cdot A = Y \ cdot $.
A $ A_ (m \ times n) = (a_ (ij)) $ mátrixra transzponáltat $ $__ mátrixnak nevezzük (n \ x m) ^ (T) = (a_ (ij) ^ (T)) $ , azokhoz az elemekhez, amelyek $ a_ (ij) ^ (T) = a_ (ji) $.
Egyszerűen fogalmazva, a $ A ^ T $ transzponált mátrix megszerzéséhez le kell cserélnie az eredeti $ A $ mátrix oszlopait a megfelelő sorokra a következő elv szerint: ha az első sor volt, az első oszlop lesz ; volt egy második sor - lesz egy második oszlop; volt egy harmadik sor - lesz egy harmadik oszlop és így tovább. Például keressük a transzponált mátrixot a $ A_ mátrixba (3 -szor 5) $:

Ennek megfelelően, ha az eredeti mátrix $ 3 \ x 5 $ volt, akkor az átültetett mátrix $ 5 \ x 3 $.
A mátrixok műveleteinek néhány tulajdonsága.
Itt feltételezzük, hogy a $ \ alpha $, $ \ beta $ néhány szám, és az $ A $, $ B $, $ C $ mátrixok. Az első négy ingatlannál a neveket tüntettem fel, a többi az első négyhez hasonlóan nevezhető el.
1. előadás
MÁTRIX
A mátrixok meghatározása és típusai
Meghatározás 1.1.Mátrix méret T NS téglalap alakú számok (vagy más objektumok) táblájának nevezik m vonalak és n oszlopok.
A mátrixokat a latin ábécé nagybetűvel (pl. A, B, C, ... A mátrixot alkotó számokat (vagy más objektumokat) hívják elemeket mátrixok. A mátrix elemei lehetnek függvények. A mátrix elemeinek kijelöléséhez a latin ábécé kisbetűit kell használni kettős indexeléssel: аij, ahol az első index én(olvasható - és) - sorszám, második index j(olvass - zhi) – oszlop száma.
Meghatározás 1.2. A mátrixot ún négyzet n- sorrendben, ha sorainak száma megegyezik az oszlopok számával, és megegyezik a számmal NS
Négyzetes mátrix esetén a fogalmakat vezetik be fő és másodlagos Diagonal vonalok.
Meghatározás 1.3.Fő átlós egy négyzetes mátrix azonos indexű elemekből áll, azaz Ezek az elemek: a 11, 22, ...
Meghatározás 1.4. átlós ha a főátló elemeinek kivételével minden elem nulla
Meghatározás 1.5. A négyzet mátrixot ún háromszög alakú ha minden eleme a főátló alatt (vagy felett) található, akkor nulla.
Meghatározás 1.6. Négyzet alakú mátrix NS- Az a sorrend, amelyben a főátló minden eleme egyenlő eggyel, a többi pedig nulla, az ún. egyetlen mátrix n-rendű, és ezt a betű jelöli E.
Meghatározás 1.7. Bármilyen méretű mátrixot hívunk nulla, vagy null mátrix, ha minden eleme nulla.
Meghatározás 1.8. Egysoros mátrixot hívnak mátrix-sor.
Meghatározás 1.9. Egy oszlopos mátrixot hívunk oszlop mátrix.
A = (a 11 a 12 ... a 1n) - sormátrix;
Meghatározás 1.10. Két mátrix Aés V azonos méretűek egyenlő, ha ezen mátrixok összes megfelelő eleme egyenlő egymással, azaz aij = bij bármilyen én= 1, 2, ..., T; j = 1, 2,…, n.
Mátrix műveletek
A mátrixokon, valamint a számokon számos művelet hajtható végre. A mátrixok fő műveletei a mátrixok összeadása (kivonása), a mátrix számmal való megszorzása és a mátrix szorzása. Ezek a műveletek hasonlóak a számokkal végzett műveletekhez. Egy speciális művelet a mátrix transzponálása.
Egy mátrix szorzása egy számmal
Meghatározás 1.11.Az A mátrix szorzata a számmalλ -t mátrixnak nevezzük B = A, amelynek elemeit a mátrix elemeinek megszorzásával nyerjük Aλ számmal .
1.1. Példa Keresse meg a mátrix szorzatát A = ![]() az 5 -ös számhoz.
az 5 -ös számhoz.
Megoldás... .◄ 5A = ![]()
A mátrix számmal való megszorzásának szabálya: hogy egy mátrixot megszorozzunk egy számmal, a mátrix összes elemét meg kell szorozni ezzel a számmal.
Következmény.
1. Minden mátrix elem közös tényezője kivehető a mátrix előjelből.
2. A mátrix szorzata A van egy nulla mátrix a 0 számhoz: A· 0 = 0 .
Mátrix összeadás
Meghatározás 1.12.Két A és B mátrix összege azonos méretű t n mátrixnak hívják VAL VEL= A+ V, amelynek elemeit a mátrix megfelelő elemeinek hozzáadásával kapjuk Aés mátrixok V, azaz cij = aij + bij számára i = 1, 2, ..., m; j= 1, 2, ..., n(azaz a mátrixokat elemenként adjuk hozzá).
Következmény. Mátrix összeg A nulla mátrix esetén egyenlő az eredeti mátrixszal: A + O = A.
1.2.3. A mátrixok kivonása
Két mátrix különbsége ugyanazt a méretet határozzák meg az előző műveletek során: A - B = A + ( - 1) V.
Meghatározás 1.13. Mátrix –A = (- 1) A hívott szemben mátrix A.
Következmény. Az ellentétes mátrixok összege megegyezik a nulla mátrixszal : A + (–A) = O.
Mátrix szorzás
Meghatározás 1.14.Az A mátrix szorzása a B mátrixszal akkor határozzák meg, ha az első mátrix oszlopainak száma megegyezik a második mátrix sorainak számával. Azután mátrixok szorzata ilyen mátrixot neveznek , amelynek minden eleme cij egyenlő az elemek szorzatának összegével én-a mátrix harmadik sora A a megfelelő elemeken j a mátrix oszlopa B.
1.4. Példa Számítsa ki a mátrixok szorzatát А В, ahol
A = 
= ![]()
1.5. Példa Keresse meg a Matrix termékeket ABés VA, ahol
Megjegyzések. Az 1.4–1.5. Példákból az következik, hogy a mátrixszorzás művelete eltér a számok szorzásától:
1) ha a mátrixok szorzata AB létezik, akkor a tényezők helyenként történő átrendezése után a mátrixok szorzata VA nem létezhet. Valóban, az 1.4. Példában az AB mátrixok szorzata létezik, de a BA termék nem létezik;
2) akkor is, ha a művek ABés VA léteznek, akkor a termék eredménye különböző méretű mátrixok lehetnek. Abban az esetben, ha mindkettő működik ABés VA mindkettő létezik - azonos méretű mátrixok (ez csak akkor lehetséges, ha az azonos sorrendű négyzetmátrixokat megszorozzuk), majd a kommutatív (transzponálható) szaporodási törvény még mindig nem áll fenn, azok. A B B A, mint az 1.5;
3) ha azonban megszorozzuk a négyzetmátrixot A az identitás mátrixon E akkor ugyanabban a sorrendben AE = EA = A.
Így az identitásmátrix a mátrixszorzásban ugyanazt a szerepet játssza, mint az 1 -es szám a számok szorzásában;
4) két nem nulla mátrix szorzata egyenlő lehet a nulla mátrixszal, vagyis abból a tényből, hogy A B= 0, ebből nem következik A = 0 vagy B = 0.
1. évfolyam, magasabb matematika, tanulunk mátrixokés az alapvető műveleteket. Itt rendszerezzük a mátrixokkal elvégezhető alapvető műveleteket. Hol kezdjem az ismerkedést a mátrixokkal? Természetesen a legegyszerűbbektől - definíciók, alapfogalmak és legegyszerűbb műveletek. Biztosítjuk, hogy a mátrixokat mindenki megérti, aki legalább egy kis időt szentel nekik!
A mátrix definíciója
Mátrix Ez egy téglalap alakú táblázat az elemekről. Nos, ha leegyszerűsítve - számok táblázata.
A mátrixokat általában nagybetűs latin betűk jelzik. Például a mátrix A , mátrix B stb. A mátrixok különböző méretűek lehetnek: téglalap alakú, négyzet alakú, vannak sor- és oszlopmátrixok is, amelyeket vektoroknak neveznek. A mátrix méretét a sorok és oszlopok száma határozza meg. Például írjunk egy téglalap alakú mátrixot m tovább n , ahol m - a sorok száma, és n - az oszlopok száma.

Elemek, amelyekhez i = j (a11, a22, .. ) alkotják a mátrix fő átlóját, és átlónak nevezzük.
Mit lehet tenni a mátrixokkal? Összeadás / kivonás, megszorozzuk egy számmal, szaporodnak egymás között, átültetni... Most ezekről az alapműveletekről a mátrixokon sorrendben.
Mátrix összeadási és kivonási műveletek
Azonnal figyelmeztetünk, hogy csak azonos méretű mátrixokat adhat hozzá. Az eredmény egy azonos méretű mátrix. A mátrixok hozzáadása (vagy kivonása) egyszerű - csak hozzá kell adni a megfelelő elemeket ... Mondjunk példát. Adjunk hozzá két A és B mátrixot kettesével.

A kivonást analógia útján hajtják végre, csak az ellenkező előjellel.
Bármely mátrix tetszőleges számmal megszorozható. Ezt csináld meg, minden elemét meg kell szorozni ezzel a számmal. Például megszorozzuk az első példa A mátrixát az 5 -ös számmal:

Mátrixszorzási művelet
Nem minden mátrixot lehet megszorozni egymással. Például két mátrixunk van - A és B. Csak akkor szorozhatók egymással, ha az A mátrix oszlopainak száma megegyezik a B mátrix sorainak számával. Ebben az esetben a kapott mátrix minden eleme, amely az i. sorban és a j oszlopban áll, egyenlő lesz az első tényező i. sorának és a j a második... Ennek az algoritmusnak a megértéséhez írjuk le, hogyan szorozunk két négyzetmátrixot:

És egy példa valós számokkal. Szorozzuk meg a mátrixokat:

Mátrix transzponáló művelet
A mátrix transzponálás olyan művelet, amelyben a megfelelő sorokat és oszlopokat felcserélik. Például transzponáljuk az A mátrixot az első példából:

Egy mátrix meghatározója
A determináns, de a determináns a lineáris algebra egyik alapfogalma. Valamikor az emberek lineáris egyenleteket találtak ki, mögöttük pedig egy determinánst kellett kitalálniuk. Ennek eredményeként meg kell küzdenie mindezzel, tehát az utolsó spurt!
A determináns egy négyzetes mátrix számszerű jellemzője, amely sok probléma megoldásához szükséges.
A legegyszerűbb négyzetes mátrix determinánsának kiszámításához ki kell számítania a fő és a másodlagos átló elemeinek szorzatai közötti különbséget.
Az elsőrendű mátrix determinánsa, azaz egy elemből áll, egyenlő ezzel az elemmel.
Mi van, ha a mátrix háromszor három? Itt már bonyolultabb, de megbirkózhat.
Egy ilyen mátrix esetében a determináns értéke megegyezik a főátló elemeinek szorzatával, valamint a főátlóval párhuzamos felületű háromszögeken fekvő elemek szorzatának összegével, amelyből a kivonjuk az oldalátló elemeit és a háromszögekre fekvő elemek szorzatát a párhuzamos oldalátló oldalával.
Szerencsére a gyakorlatban ritkán kell kiszámítani a nagy mátrixok meghatározóit.
Itt a mátrixokkal kapcsolatos alapvető műveleteket ismertettük. Természetesen a való életben soha nem is találkozhat egy csipetnyi mátrix egyenletrendszerrel, vagy fordítva - sokkal nehezebb esetekkel kell szembenéznie, amikor valóban törnie kell a fejét. Ilyen esetekben van professzionális hallgatói szolgálat. Kérjen segítséget, szerezzen minőségi és részletes megoldást, élvezze tanulmányi sikereit és szabadidejét.
Ahhoz, hogy az A mátrixot tetszőleges α számmal megszorozzuk, szüksége van a mátrix elemeire A megszorozzuk az α számmal, azaz a mátrix szám szerinti szorzata a következő lesz:

1. példa. Keresse meg a Mátrix 3 -at A mátrixra

Megoldás. A definíciónak megfelelően megszorozzuk a mátrix elemeit A 3 -ra és kap

Ez egy nagyon egyszerű példa volt arra, hogy a mátrixot megszorozzuk egy számmal egész számokkal. Vannak egyszerű példák is előtte, de már olyanok, ahol a mátrixok tényezői és elemei között vannak törtek, változók (betűjelölések), mert a szorzás törvényei nem csak egész számokra érvényesek, így soha nem árt megismételni őket.
2. példa. Aα számmal, ha  ,
.
,
.
Aα -val, nem felejtve el, hogy a törtek szorzásakor az első tört számlálóját megszorozzuk az első tört számlálójával, és a szorzót beírjuk a számlálóba, és az első tört nevezőjét megszorozzuk a második tört nevezőjével és a terméket beírják a nevezőbe. Az új mátrix első sorának második elemének fogadásakor a kapott frakció 2 -vel csökkent, ezt meg kell tenni. Kapunk

3. példa. Végezze el a mátrixszorzási műveletet Aα számmal, ha
,
.
Megoldás. Szorozzuk meg a mátrix elemeit Aα -val, anélkül, hogy összezavarodna a betűjelzésben, ne felejtsen el mínuszt hagyni az új mátrix második sora második eleme előtt, és emlékezzen arra, hogy egy számnak az inverz számával való megszorzása egy (az első a harmadik sor eleme). Kapunk
 .
.
4. példa. Végezze el a mátrixszorzási műveletet Aα számmal, ha  ,
.
,
.
Megoldás. Ne feledje, hogy amikor egy hatvány számát megszorozzuk egy hatvány számával, a kitevők összeadódnak. Kapunk
 .
.
Ez a példa többek között egyértelműen bizonyítja, hogy a mátrix számmal való megszorzásának műveletei fordított sorrendben olvashatók (és írhatók), és ezt úgy hívják, hogy állandó tényezőt helyeznek a mátrix elé.
Kombinálva mátrixok összeadása és kivonása a mátrix számmal való megszorzásának művelete különféle mátrix kifejezéseket képezhet, például 5 A − 3B , 4A + 2B .
A mátrix számmal való megszorzásának tulajdonságai
(itt A, B - mátrixok, - számok, 1 - első számú)
1. ![]()
2. ![]()
3. ![]()
Az (1) és (2) tulajdonságok összekapcsolják a mátrix számmal való szorzását mátrixok hozzáadásával. Nagyon fontos összefüggés van a mátrix számmal való megszorzása és a mátrixok szorzása között is:
vagyis ha a mátrixok szorzatában az egyik tényezőt megszorozzuk egy számmal, akkor a teljes szorzatot megszorozzuk egy számmal.
Ez a módszertani útmutató segít megtanulni a teljesítést mátrixokkal végzett műveletek: mátrixok összeadása (kivonása), mátrix transzponálása, mátrixok szorzása, az inverz mátrix megtalálása. Minden anyag egyszerű és hozzáférhető formában kerül bemutatásra, releváns példákat adunk, így még egy felkészületlen személy is megtanulhat mátrixokkal végrehajtani a műveleteket. Önellenőrzéshez és önellenőrzéshez ingyenesen letölthet egy mátrix számológépet >>>.
Megpróbálom minimalizálni az elméleti számításokat, helyenként magyarázatok lehetségesek "ujjakon" és tudománytalan kifejezések használata. Szilárd elmélet szerelmesei, kérem, ne kritizáljanak, a mi feladatunk az megtanulhat mûveleteket végrehajtani mátrixokkal.
A téma szupergyors előkészítéséhez (aki "lángol") van egy intenzív pdf-tanfolyam Mátrix, determináns és teszt!
A Mátrix bármely téglalap alakú táblázat elemeket... Mint elemeket figyelembe vesszük a számokat, vagyis a numerikus mátrixokat. ELEM Egy kifejezés. Célszerű megjegyezni a kifejezést, gyakran találkozni fog vele, nem véletlenül használtam vastag betűtípust a kiemeléshez.
Kijelölés: a mátrixokat általában nagy latin betűkkel jelölik
Példa: Vegyünk egy két-három mátrixot:
![]()
Ez a mátrix hatból áll elemeket:
A mátrixon belül minden szám (elem) önmagában létezik, vagyis nincs szó kivonásról: ![]()
Ez csak egy táblázat (számkészlet)!
Mi is egyetértünk ne rendezd át számokat, hacsak a magyarázatok másként nem rendelkeznek. Minden számnak saját helye van, és nem keverhető!
A kérdéses mátrixnak két sora van: 
és három oszlop: 
ALAPÉRTELMEZETT: amikor a mátrix méretéről beszélünk, akkor először jelezze a sorok számát, és csak ezután - az oszlopok számát. Most szétszedtünk egy kettő-három mátrixot.
Ha a mátrix sorainak és oszlopainak száma megegyezik, akkor a mátrixot hívjuk négyzet, például:  -három-három mátrix.
-három-három mátrix.
Ha a mátrix egy oszlopot vagy egy sort tartalmaz, akkor az ilyen mátrixokat is hívják vektorok.
Valójában az iskola óta ismerjük a mátrix fogalmát, tekintsünk például egy "x" és "játék" koordinátájú pontot :. Lényegében egy pont koordinátái egy-egy mátrixba vannak írva. Egyébként íme egy példa, hogy miért számít a számok sorrendje: és a sík két teljesen különböző pontja.
Most menjünk közvetlenül a tanulmányhoz műveletek mátrixokkal:
1) Első lépés. A mínusz eltávolítása a mátrixból (a mínusz hozzáadása a mátrixhoz).
Vissza a mátrixunkhoz  ... Amint észrevette, ebben a mátrixban túl sok negatív szám található. Nagyon kényelmetlen abból a szempontból, hogy különböző műveleteket hajtunk végre a mátrixszal, kényelmetlen ennyi mínuszt írni, és csak csúnyán néz ki a tervezésben.
... Amint észrevette, ebben a mátrixban túl sok negatív szám található. Nagyon kényelmetlen abból a szempontból, hogy különböző műveleteket hajtunk végre a mátrixszal, kényelmetlen ennyi mínuszt írni, és csak csúnyán néz ki a tervezésben.
Mozgassa a mínuszt a mátrixon kívül, ha megváltoztatja az MINDEN mátrix elem előjelét:
Nullánál, ahogy érted, a jel nem változik, nulla - ez nulla Afrikában.
Fordított példa:  ... Csúnyán néz ki.
... Csúnyán néz ki.
Adjunk hozzá egy mínuszt a mátrixhoz az EGYES mátrixelem előjelének megváltoztatásával:

Nos, sokkal szebb lett. És ami a legfontosabb, KÖNNYEBB lesz bármilyen műveletet végrehajtani a mátrix segítségével. Mert van egy ilyen matematikai népi előjel: minél több a hátrány, annál több a zűrzavar és a hiba.
2) Második akció. Egy mátrix szorzása egy számmal.
Példa:
![]()
Egyszerű, ahhoz, hogy egy mátrixot megszorozzunk egy számmal, szükség van minden egyes a mátrix elemét megszorozzuk a megadott számmal. Ebben az esetben az első három.
Egy másik hasznos példa:
 - mátrixszorzás törtével
- mátrixszorzás törtével
Először nézzük meg, mit tegyünk. NINCS SZÜKSÉG:
NEM SZÜKSÉGES töredék beírása a mátrixba, egyrészt csak bonyolítja a mátrix további műveleteit, másrészt megnehezíti a tanár számára a megoldás ellenőrzését (különösen, ha  - a feladat végső válasza).
- a feladat végső válasza).
És főleg, NINCS SZÜKSÉG oszd el a mátrix minden elemét mínusz héttel:

A cikkből Matematika próbababáknak, vagy hol kezdjem, emlékezünk arra, hogy a magasabb matematikában vesszővel tizedes törteket minden lehetséges módon megpróbáljuk elkerülni.
Az egyetlen, ami kívánatos Ebben a példában egy mínusz bevezetése a mátrixba:

De ha ÖSSZES A mátrix elemei oszthatók 7 -gyel maradék nélkül, akkor lehetséges (és szükséges!) felosztás lenne.
Példa:

Ebben az esetben lehetséges és SZÜKSÉGES megszorozzuk a mátrix összes elemét, mivel a mátrix összes száma osztható 2 -vel maradék nélkül.
Megjegyzés: a magasabb matematika elméletében nincs iskolai „megosztás” fogalom. Az "oszd meg ezzel" kifejezés helyett mindig azt mondhatod, hogy "ezt szorozd töredékkel". Vagyis az osztás a szorzás speciális esete.
3) Harmadik akció. Mátrix transzponálás.
A mátrix transzponálásához be kell írnia sorait az átültetett mátrix oszlopaiba.
Példa:
Mátrix transzponálása
Itt csak egy sor van, és a szabály szerint egy oszlopba kell írni:
- átültetett mátrix.
Az átültetett mátrixot általában felső index vagy vonal jelzi a jobb felső sarokban.
Példa lépésről lépésre:
Mátrix transzponálása 
Először írjuk át az első sort az első oszlopba:

Ezután a második sort átírjuk a második oszlopba: 
Végül a harmadik sort átírjuk a harmadik oszlopba:

Kész. Durván szólva az átültetés azt jelenti, hogy a mátrixot egy oldalra fordítjuk.
4) Negyedik akció. A mátrixok összege (különbsége).
A mátrixok összege egyszerű művelet.
NEM MINDEN HALÓ HOZZÁFÉRHETŐ. A mátrixok összeadásának (kivonásának) elvégzéséhez szükséges, hogy azonos méretűek legyenek.
Például, ha kapunk egy kettő-kettő mátrixot, akkor azt csak két-kettő mátrixszal lehet hozzáadni, mással nem! 
Példa:
Mátrixok hozzáadása ![]() és
és ![]()
A mátrixok hozzáadásához hozzá kell adni a megfelelő elemeket:

A mátrixok különbségére a szabály hasonló, meg kell találni a megfelelő elemek különbségét.
Példa:
Keresse meg a mátrixok közötti különbséget ![]() ,
, ![]()

És hogyan lehet ezt a példát könnyebben megoldani, nehogy összezavarodjon? Célszerű megszabadulni a felesleges mínuszoktól, ehhez adunk egy mínuszt a mátrixhoz:

Megjegyzés: a magasabb matematika elméletében nincs iskolai "kivonás" fogalma. Ahelyett, hogy azt mondaná, hogy "vonja le ezt", mindig azt mondhatja, hogy "adjon ehhez negatív számot". Vagyis a kivonás az összeadás speciális esete.
5) Ötödik intézkedés. Mátrix szorzás.
Milyen mátrixokat lehet megszorozni?
Ahhoz, hogy a mátrixot megszorozzuk a mátrixszal, szüksége van hogy a mátrix oszlopainak száma egyenlő legyen a mátrix sorainak számával.
Példa:
Meg lehet szorozni egy mátrixot egy mátrixszal?

Ez azt jelenti, hogy meg lehet szorozni ezeket a mátrixokat.
De ha a mátrixokat átrendezzük, akkor ebben az esetben a szorzás már lehetetlen!

Ezért a szorzás nem lehetséges:

Nem olyan ritka, hogy trükkös feladatokkal találkoznak, amikor a tanulót arra kérik, hogy szaporítsák a mátrixokat, amelyek sokszorozása nyilvánvalóan lehetetlen.
Meg kell jegyezni, hogy számos esetben mindkét irányban lehetséges a mátrixok szorzása.
Például mátrixok esetén, és mind a szorzás, mind a szorzás lehetséges
 A Nem elég elemek kezelése és funkciói mod
A Nem elég elemek kezelése és funkciói mod Hibaelhárítás TLauncher
Hibaelhárítás TLauncher Miért nem az Instagram keresi a helyét: a fő okok?
Miért nem az Instagram keresi a helyét: a fő okok? Hogyan lehet törölni a gyorsítótárat a vk alkalmazásban
Hogyan lehet törölni a gyorsítótárat a vk alkalmazásban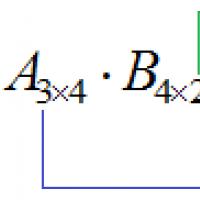 Alapműveletek mátrixokon (összeadás, szorzás, transzponálás) és tulajdonságaik
Alapműveletek mátrixokon (összeadás, szorzás, transzponálás) és tulajdonságaik Lítium -polimer akkumulátorok
Lítium -polimer akkumulátorok A logikai kifejezések azonos konverziói
A logikai kifejezések azonos konverziói