Logikai műveletek igazságtáblái, hogyan kell megoldani. A logikai kifejezések azonos konverziói
Ma az informatika nevű témáról fogunk beszélni. Igazságtábla, függvénytípusok, végrehajtásuk sorrendje - ezek a fő kérdéseink, amelyekre megpróbálunk választ találni a cikkben.
Általában ezt a kurzust középiskolában oktatják, de a diákok nagy száma az oka annak, hogy néhány jellemzőt nem értenek. És ha ennek fogja szentelni az életét, akkor egyszerűen nem nélkülözheti az informatika egységes államvizsga letételét. Igazságtábla, komplex kifejezések átalakítása, logikai problémák megoldása - mindez megtalálható a jegyben. Most közelebbről megvizsgáljuk ezt a témát, és segítünk abban, hogy több pontot szerezzen a vizsgán.
A logika tárgya
Mi ez a tantárgy - informatika? Igazságtábla - hogyan kell felépíteni? Miért van szükség a logika tudományára? Most ezekre a kérdésekre válaszolunk.
Az informatika meglehetősen izgalmas téma. Ez nem okozhat nehézségeket a modern társadalomban, mert minden, ami körülvesz minket, így vagy úgy, számítógépre utal.
A logikai tudomány alapjait középiskolai tanárok oktatják informatikaórákon. Igazságtáblázatok, függvények, kifejezések egyszerűsítése - mindezt a számítástechnika tanárának kell megmagyaráznia. Ez a tudomány egyszerűen szükséges az életünkben. Nézze meg közelebbről, minden engedelmeskedik bizonyos törvényeknek. Dobtad a labdát, felrepült, de aztán visszaesett a földre, ez a fizika törvényeinek és a gravitációs erőnek volt köszönhető. Anya levest főz és sót tesz hozzá. Miért nem kapunk gabonát, amikor megeszük? Egyszerű, a sót vízben oldják, engedelmeskedve a kémia törvényeinek.

Most figyeljen arra, hogyan beszél.
- - Ha elviszem a macskámat az állatorvosi klinikára, beoltják.
- - A mai nap nagyon nehéz volt, mert megjött a csekk.
- „Nem akarok egyetemre menni, mert ma kollokvium lesz”, stb.
Minden, amit mond, köteles betartani a logika törvényeit. Ez vonatkozik mind az üzleti, mind a baráti beszélgetésre. Éppen ezért szükséges megérteni a logika törvényeit, hogy ne véletlenül cselekedjünk, hanem biztosak lehessünk az események kimenetelében.
Funkciók
Annak érdekében, hogy összeállítson egy igazságtáblázatot az Ön számára javasolt problémára, ismernie kell a logikai függvényeket. Ami? Egy logikai függvénynek vannak változói, amelyek állítások (igazak vagy hamisak), és maga a függvény értéke adja meg a választ a kérdésre: "Igaz vagy hamis a kifejezés?"
Minden kifejezés a következő értékeket veszi fel:
- Igaz vagy hamis.
- És vagy L.
- 1 vagy 0.
- Plusz vagy mínusz.
Itt részesítse előnyben az Ön számára kényelmesebb módszert. Az igazságtábla összeállításához fel kell sorolnunk a változók összes kombinációját. Számukat a következő képlettel kell kiszámítani: 2 n -ig. A számítás eredménye a lehetséges kombinációk száma, az n változó ebben a képletben az állapot változóinak számát jelöli. Ha a kifejezésnek sok változója van, akkor használhat számológépet, vagy készíthet magának egy kis táblázatot kettes hatványra emelésével.
Összesen hét funkciót vagy kapcsolatot különböztetünk meg a logikában, amelyek összekötik a kifejezéseket:
- Szorzás (kötőszó).
- Összeadás (diszjunkció).
- Következtetés (implikáció).
- Egyenértékűség.
- Inverzió.
- Schaeffer ütése.
- Pierce nyila.
A lista első műveletét "logikai szorzásnak" nevezik. Grafikusan megjelölhető fordított pipa, & vagy *. A listánk második művelete logikai összeadás, grafikusan pipa, +jelzéssel. Az implikációt logikai következménynek nevezik, feltételről következményre mutató nyílként jelölik. Az egyenértékűséget kétfejű nyíl jelzi, a függvénynek csak azokban az esetekben van valódi értéke, amikor mindkét érték vagy "1" vagy "0" értéket vesz fel. Az inverziót logikai tagadásnak nevezzük. Schaeffer ütését függvénynek nevezzük, amely tagadja a konjunkciót, Peirce nyílját pedig diszjunkciót tagadó függvénynek.
Alapvető bináris függvények
A logikai igazságtáblázat segít megtalálni a választ a feladatban, ehhez azonban emlékeznie kell a bináris függvények tábláira. Ezeket ebben a részben fogjuk közölni.

Kötőszó (szorzás). Ha kettő van, akkor ennek eredményeként megkapjuk az igazságot, minden más esetben hazugságot.
Az eredmény hamis logikai összeadással, csak két hamis bemenet esetén van.
Egy logikai következménynek csak akkor van hamis eredménye, ha a feltétel igaz, és a hatás hamis. Itt hozhat egy példát az életből: „Cukrot akartam venni, de a bolt zárva volt”, ezért a cukrot soha nem vették meg.
Az egyenértékűség csak akkor igaz, ha a bemeneti adatok értékei megegyeznek. Vagyis párokkal: "0; 0" vagy "1; 1".

Inverzió esetén minden elemi, ha a bemeneten igaz kifejezés van, akkor hamisra konvertálódik, és fordítva. A képen látható, hogyan jelenik meg grafikusan.
A Schiffer -ütés csak hamis eredményt ad, ha két igaz kifejezés létezik.
Pierce nyílja esetén a függvény csak akkor lesz igaz, ha csak hamis kifejezéseket használunk bemenetként.
Milyen sorrendben kell logikai műveleteket végrehajtani
Kérjük, vegye figyelembe, hogy igazságtáblázatok készítése és kifejezések egyszerűsítése csak akkor lehetséges, ha a műveletek sorrendje helyes. Ne feledje, milyen sorrendben kell elvégezni őket, ez nagyon fontos a helyes eredmény eléréséhez.
- logikai tagadás;
- szorzás;
- kiegészítés;
- következmény;
- egyenértékűség;
- a szorzás tagadása (Schaeffer stroke);
- az adalék tagadása (Pierce nyíl).
1. példa
Most azt javasoljuk, hogy vegyünk egy példát egy igazságtábla létrehozására 4 változóra. Ki kell deríteni, hogy milyen esetekben F = 0 az egyenlethez: notA + B + C * D
Erre a feladatra a válasz az alábbi kombinációk felsorolása lesz: "1; 0; 0; 0", "1; 0; 0; 1" és "1; 0; 1; 0". Mint látható, az igazságtábla elkészítése meglehetősen egyszerű. Még egyszer szeretném felhívni a figyelmet a cselekvések sorrendjére. Egy konkrét esetben ez a következő volt:
- Az első egyszerű kifejezés megfordítása.
- A harmadik és a negyedik kifejezés együttállása.
- A második kifejezés szétválasztása a korábbi számítások eredményeivel.
2. példa

Most megvizsgálunk egy másik feladatot, amely megköveteli az igazságtábla felépítését. A számítástechnika (példákat az iskolai tanfolyamból vettünk) is lehet feladat. Vessünk egy pillantást az egyikre. Bűnös -e Vanya a labda ellopásában, ha a következők ismertek:
- Ha Vanya nem lopott, vagy Petya lopott, akkor Seryozha részt vett a lopásban.
- Ha Vanya nem bűnös, akkor Seryozha sem lopta el a labdát.
Bemutatjuk a jelöléseket: I - Vanya ellopta a labdát; P - Petya lopott; S - Seryozha lopott.
E feltétel szerint összeállíthatjuk az egyenletet: F = ((nem-I + P) implikáció C) * (nem-I implikáció nem C). Szükségünk van azokra a lehetőségekre, ahol a függvény valódi értéket vesz fel. Ezután létre kell hoznia egy táblázatot, mivel ennek a függvénynek akár 7 művelete is van, ezeket kihagyjuk. Csak a bemeneti adatokat és az eredményt adjuk meg.
Vegye figyelembe, hogy ebben a feladatban a "0" és "1" jelek helyett pluszt és mínuszt használtunk. Ez is elfogadható. Olyan kombinációkra vagyunk kíváncsiak, ahol F = +. Ezek elemzése után a következő következtetést vonhatjuk le: Vanya részt vett a labda ellopásában, mivel minden olyan esetben, amikor F a +értéket veszi fel, és pozitív értékkel rendelkezik.
3. példa

Most azt javasoljuk, hogy keressük meg a kombinációk számát, ha F = 1. Az egyenlet a következő alakú: F = notA + B * A + notB. Összeállítunk egy igazságtáblát:
Válasz: 4 kombináció.
Alapvető logikai műveletek
Tagadás (inverzió), a latin inversio -ból - fordítsd meg:
A NEM részecskének felel meg, a kifejezés ROSSZ MI;
Megnevezés: nem A, A, -A;
igazság táblázat:
A logikai változó inverze igaz, ha maga a változó hamis, és fordítva, az inverz hamis, ha a változó igaz.
Példa: A = (Kint havazik).
A = (Nem igaz, hogy kint havazik)
A = (Kint nem esik a hó);
Logikai összeadás (diszjunkció), a latin disjunctio -ból - megkülönböztetem:
Megfelel az uniónak VAGY;
Megnevezés: +, vagy, vagy, V;
Igazság táblázat:
A diszjunkció akkor és csak akkor hamis, ha mindkét állítás hamis.
Példa: F = (Kint süt a nap, vagy erős szél fúj);
Logikai szorzás (kötőszó), a latin conjunctio -ból - Csatlakozom:
Megfelel az uniónak ÉS
(természetes nyelven: mind A, mind B, mind A, mind B, A együtt B, A, annak ellenére, hogy B, A, míg B);
Megnevezés: Ч ,, &, és, ^, és;
Igazság táblázat:
Egy kötőszó akkor és csak akkor igaz, ha mindkét állítás igaz.
Példa: F = (Kint süt a nap és erős szél fúj);
Bármilyen összetett állítás írható az alapvető logikai műveletek segítségével ÉS, VAGY, NEM. A logikai áramkörök segítségével ÉS, VAGY NEM lehetséges olyan logikai függvény megvalósítása, amely leírja a különböző számítógépes eszközök működését.
2) Az igazságtábla egy logikai függvényt leíró táblázat.
Ebben az esetben a "logikai függvény" olyan függvényt jelent, amelyben a változók (függvényparaméterek) értékei és maga a függvény értéke logikai igazságot fejeznek ki. Például a kétértékű logikában felvehetik az "igaz" vagy "hamis" értékeket (vagy, vagy).
A függvények táblázatos meghatározása nemcsak a logikában található meg, hanem a táblázatok különösen kényelmesnek bizonyultak a logikai függvények számára, és a 20. század elejétől ezt a különleges nevet kapták hozzájuk. Az igazságtáblákat különösen gyakran használják a Boole-algebrában és hasonló többértékű logikai rendszerekben.
A kötőszó logikai művelet, amely alkalmazásában a lehető legközelebb áll az "és" kötőszóhoz. Logikai szorzás, néha csak "ÉS".
A diszjunkció egy logikai művelet, amely alkalmazásában a lehető legközelebb áll a „vagy” kötőszóhoz „vagy ez, vagy ez, vagy mindkettő egyszerre” értelmében. logikus kiegészítés, néha csak "VAGY".
Az implikáció bináris logikai összekötő, alkalmazásában a "ha ... akkor ..." kötőszavakhoz közel áll. más alakú és másik irányba irányított nyilakat is használnak (a pont mindig a hatást jelzi).
Az egyenértékűség (vagy ekvivalencia) két helyből álló logikai művelet. Általában ≡ vagy symbol szimbólum jelzi.
7. Logikai kifejezések, logikai kifejezések igazságtáblái.
A logikai kifejezés egy rekord vagy egy verbális állítás, amely az állandókkal együtt szükségszerűen változó mennyiségeket (objektumokat) is tartalmaz. E változók értékeitől függően a logikai kifejezés két lehetséges érték egyikét veheti fel: IGAZ (logikai 1) vagy HAMIS (logikai 0)
A komplex logikai kifejezés egy logikai kifejezés, amely egy vagy több egyszerű (vagy összetett) logikai kifejezésből áll, amelyek logikai műveletekhez kapcsolódnak.
Logikai műveletek és igazságtáblázatok
Logikai szorzás CONJUNCTION - ez az új komplex kifejezés csak akkor lesz igaz, ha mindkét eredeti egyszerű kifejezés igaz. A kötőszó két logikai kifejezés összeköttetését határozza meg az I egység használatával.
Logikai összeadás - KIKAPCSOLÁS - ez az új összetett kifejezés akkor és csak akkor lesz igaz, ha az eredeti (egyszerű) kifejezések közül legalább az egyik igaz. A diszjunkció két logikai kifejezés kapcsolatát határozza meg az OR kötőszóval
Logikai tagadás: INVERZIÓ - ha az eredeti kifejezés igaz, akkor a tagadás eredménye hamis lesz, és fordítva, ha az eredeti kifejezés hamis, akkor a tagadás eredménye igaz lesz / Ez a művelet azt jelenti, hogy a részecske NEM vagy a ROSSZ szó az eredeti logikai kifejezéshez, a MI
Logikai következtetés: IMPLICATION - két egyszerű logikai kifejezést kapcsol össze, amelyek közül az első egy feltétel (A), a második (B) ennek a feltételnek a következménye. Az IMPLIKÁCIÓ eredménye csak akkor hamis, ha az A feltétel igaz és a B következmény hamis. Ezt az "ezért" szimbólum jelöli, és a HA ..., AKKOR ... szavakkal fejezik ki
Logikai ekvivalencia: EQUIVALENCE - meghatározza két egyszerű A és B logikai kifejezés összehasonlításának eredményét. Az EQUIVALENCE eredménye egy új logikai kifejezés, amely akkor és csak akkor lesz igaz, ha mindkét eredeti kifejezés egyszerre igaz vagy hamis. Az "egyenértékűség" szimbólum jelzi
A logikai műveletek végrehajtásának sorrendje egy összetett logikai kifejezésben:
1.fordítás
2. kötőszó
3. diszjunkció
4. implikáció
5. egyenértékűség
A zárójeleket a megadott műveleti sorrend megváltoztatására használjuk.
Igazságtáblák készítése összetett kifejezésekhez:
Sorok száma = 2n + két sor a címhez (n az egyszerű utasítások száma)
Oszlopok száma = változók száma + logikai műveletek száma
A táblázat felépítésekor figyelembe kell venni az eredeti kifejezések 0 és 1 logikai értékeinek minden lehetséges kombinációját. Ezután határozza meg a műveletek sorrendjét, és készítsen táblázatot, figyelembe véve a fő logikai műveletek igazságtábláit.
PÉLDA: összeállít egy igazságtáblát egy komplex logikai kifejezésből D = notA & (B + C)
A, B, C - három egyszerű állítás, ezért:
sorok száma = 23 +2 = 10 (n = 3, mivel a bemeneten három elem van A, B, C)
oszlopok száma: 1) A
4) nem A az A fordítottja (jelöljük E -vel)
5) A B + C egy diszjunkciós művelet (jelölje F)
6) D = notA & (B + C), azaz D = E & F egy konjunkciós művelet
A B C E = nem A (nem 1) F = B + C (2 + 3) D = E&F (4 * 5)
A logika algebrája
A logika algebrája
A logika algebrája(eng. logika algebra) - a matematikai logika egyik fő szakasza, amelyben az algebra módszereit használják a logikai transzformációkban.
A logika algebrájának alapítója J. Boole angol matematikus és logikus (1815-1864), aki logikai tanítását az algebra és a logika közötti analógiára alapozta. Bármilyen állítást leírt az általa kidolgozott nyelv szimbólumai felhasználásával, és "egyenleteket" kapott, amelyek igazsága vagy hamissága bizonyos logikai törvények alapján bizonyítható, például a kommutativitás, a disztributivitás, az asszociativitás stb.
Modern logika algebra a matematikai logika egyik ága, és az állítások logikai műveleteit tanulmányozza az igazságértékük (igaz, hamis) szempontjából. Az állítások lehetnek igazak, hamisak, vagy különböző arányban tartalmazhatnak igazat és hamisat.
Logikus kijelentés Minden olyan kijelentő mondat, amelyre vonatkozóan egyértelműen kijelenthető, hogy tartalma igaz vagy hamis.
Például: „3 -szor 3 egyenlő 9 -vel”, „Arhangelszk Vologdától északra” igaz állítások, és „Öt kevesebb, mint három”, „A Mars csillag” hamis.
Nyilvánvaló, hogy nem minden mondat lehet logikus kijelentés, hiszen nem mindig van értelme hamisságáról vagy igazságáról beszélni. Például az "A számítástechnika érdekes tantárgy" kijelentés homályos és további információkat igényel, és az "A-A osztályú AA Ivanov 10-es tanuló számára az informatika érdekes tantárgy" kijelentés, AA Ivanov érdeklődésétől függően, az "igazság" vagy a "hazugság" jelentéséről.
kivéve kétértékű propozíciós algebra, amelyben csak két értéket fogadnak el - "igaz" és "hamis" többértékű javaslati algebra. Az ilyen algebrában az "igaz" és a "hamis" jelentés mellett olyan igazságértékeket használnak, mint "valószínűleg", "lehetséges", "lehetetlen" stb.
Az algebrában a logika eltérő egyszerű(alapvető) kimondások, latin betűkkel jelöljük (A, B, C, D, ...), és összetett(összetett), amely több egyszerű elemből áll, például logikai összeköttetések használatával, mint pl "Nem", "és", "vagy", "akkor és csak akkor", "ha ... akkor"... Az így kapott összetett állítások igazságát vagy hamisságát az egyszerű állítások jelentése határozza meg.
Jelöljük, mint A a "logika algebráját sikeresen alkalmazzák az elektromos áramkörök elméletében" kijelentést, és keresztül V- "A logika algebráját a relé-érintkező áramkörök szintézisében használják."
Ezután a "Logika algebráját sikeresen alkalmazzák az elektromos áramkörök elméletében és a relé-érintkező áramkörök szintézisében" összetett állítást röviden így írhatjuk: A és B.; itt az "és" logikai összekötő. Nyilván az elemi kijelentések óta A és B. igazak, akkor az összetett állítás A és B..
Minden logikai összekötő a logikai utasítások műveleteinek tekintendő, és saját neve és megnevezése van.
Csak két logikai érték létezik: igaz igaz)és hamis (HAMIS)... Ez megfelel a digitális ábrázolásnak - 1 és 0 ... Az egyes logikai műveletek eredményei táblázat formájában rögzíthetők. Az ilyen táblákat igazságtáblázatoknak nevezik.
A Boole -algebra alapműveletei
1. Logikai tagadás, inverzió(lat. inverzió- inverzió) - logikai művelet, amelynek eredményeként egy új utasításból új állítást kapunk (például A) ( nem A.), amelyet ún az eredeti állítás tagadása, amelyet szimbolikusan egy fenti sáv ($ A↖ (-) $) vagy olyan konvenciók jelölnek, mint ¬, "nem", és így szól: "Nem A", "A hamis", "nem igaz, hogy A", "A tagadása"... Például: "A Mars a Naprendszer bolygója" (A mondás); „A Mars nem a Naprendszer bolygója” ($ A↖ (-) $); a "10 prímszám" (B utasítás) állítás hamis; a „10 nem prímszám” (B állítás) állítás igaz.
Egy műveletet egy mennyiség vonatkozásában használunk egységes... Ennek a műveletnek az értéktáblázatának formája van
A $ A↖ (-) $ állítás hamis, ha A igaz, és igaz, ha A hamis.
Geometriai szempontból a tagadás a következőképpen ábrázolható: ha A valamilyen ponthalmaz, akkor $ A↖ (-) $ az A halmaz kiegészítése, vagyis minden olyan pont, amely nem tartozik az A halmazba.
2.Összekapcsolás(lat. conjunctio- kapcsolat) - logikai szorzás, olyan művelet, amely legalább két logikai értéket (operandust) igényel, és két vagy több utasítást kapcsol össze egy link segítségével "és"(például, "A és B"), amelyet szimbolikusan a ∧ (A ∧ B) jel jelöl, és így szól: "A és B". A következő jeleket is használják az összefüggés jelzésére: A ∙ B; A & B, A és B, és néha semmilyen jel nem kerül a kijelentések közé: AB. Példa a logikai szorzásra: "Ez a háromszög egyenlő szárú és derékszögű." Egy adott állítás csak akkor lehet igaz, ha mindkét feltétel teljesül, ellenkező esetben az állítás hamis.
| A | B | A ∧ B. |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Kifejezés A ∧ V csak akkor igaz, ha mindkét állítás - Aés V igazak.
Geometriailag egy kötőszó a következőképpen ábrázolható: ha A, B A ∧ V halmazok metszéspontja van Aés V.

3. Diszjunkció(lat. diszjunkció- szétválasztás) - logikai összeadás, egy művelet, amely két vagy több utasítást köt össze egy köteg segítségével "vagy"(például, "A vagy B"), amelyet szimbolikusan a ∨ jel jelöl (A.∨ V)és ezt olvassa: "A vagy B"... A következő jeleket is használják a diszjunkció jelzésére: A + B; A vagy B; A | B... Példa a logikai összeadásra: "Az x szám osztható 3 -mal vagy 5 -tel". Ez az állítás akkor lesz igaz, ha mindkét feltétel vagy legalább az egyik feltétel teljesül.
A művelet igazságtáblázatának formája van
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Kifejezés A∨ V csak hamis, ha mindkét állítás - Aés V hamisak.
A geometriailag logikus összeadás a következőképpen ábrázolható: ha A, B Akkor néhány ponthalmaz A ∨ V A halmazok egyesülése Aés V, vagyis a négyzetet és a kört egyaránt egyesítő alak.

4. Szigorúan elválasztó diszjunkció, add modulo two- logikai művelet, amely két állítást kapcsol össze egy link segítségével "vagy", kizárólagos értelemben használva, amelyet szimbolikusan a ∨ ∨ vagy a signs ( A ∨ ∨ B, A ⊕ V) és így szól: "Vagy a vagy B"... A második kiegészítésre példa a mondás: "Ez a háromszög tompa vagy hegyes szögű." Az állítás akkor igaz, ha bármely feltétel teljesül.
A művelet igazságtáblázatának formája van
| A | V | A⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Az A ⊕ B állítás csak akkor igaz, ha az A és B állítások eltérő jelentéssel bírnak.
5. Következmény(lat. implisito- szoros összefüggésben) - logikai művelet, amely két kijelentést köt össze egy köteg segítségével "Ha akkor"összetett állítássá, amelyet szimbolikusan a → ( A → V) és így szól: "Ha A, akkor B", "A magában foglalja a B -t", "B következik A -ból", "A B -t jelent"... A ⊃ (A ⊃ B) előjelet az implikáció jelzésére is használják. Példa az implikációra: "Ha a kapott négyszög négyzet, akkor kör írható körül." Ez a művelet két egyszerű logikai kifejezést kapcsol össze, az első feltétel, a második pedig következmény. Egy művelet eredménye csak akkor hamis, ha a premissza igaz, és a hatás hamis. Például: „Ha 3 * 3 = 9 (A), akkor a Nap bolygó (B)”, az A → B implikáció eredménye hamis.
A művelet igazságtáblázatának formája van
| A | V | A→V |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Az implikáció működéséhez igaz, hogy a hazugságból bármi következhet, és az igazságból csak az igazság következhet.
6. Egyenértékűség, kettős értelem, egyenértékűség(lat. aequalis- egyenlő és valentis- érvényes) - logikus művelet, amely két állítást tesz lehetővé Aés V kap egy új nyilatkozatot A ≡ B. amely így szól: "A egyenértékű B -vel"... A következő szimbólumokat is használják az egyenértékűség jelölésére: ⇔, ∼. Ez a művelet szalagokkal fejezhető ki "Akkor és csak akkor", "szükséges és elegendő", "egyenértékű"... Példa az egyenértékűségre a következő állítás: "A háromszög akkor és csak akkor lesz téglalap alakú, ha az egyik szög 90 fokos."
Az egyenértékűségi művelet igazságtáblázatának formája van
| A | V | A∼ V |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Az egyenértékűség művelete ellentéte a második összeadási modulnak, és csak akkor kapja az "igaz" eredményt, ha a változók értékei egybeesnek.
Az egyszerű állítások jelentésének ismeretében az igazságtáblázatok alapján meg lehet határozni az összetett állítások jelentését. Fontos tudni, hogy három művelet elegendő a logika algebrájának bármely funkciójának ábrázolásához: kötőszó, diszjunkció és tagadás.
A logikai műveletek végrehajtásának prioritása a következő: negáció ( "nem") a legmagasabb prioritású, majd a konjunkció ( "és"), kötőszó után - diszjunkció ( "vagy").
A logikai változók és a logikai műveletek segítségével bármilyen logikai állítás formalizálható, azaz helyettesíthető logikai képlettel. Ugyanakkor az összetett állítást alkotó elemi állítások jelentésükben teljesen függetlenek lehetnek, de ez nem zavarja az összetett állítás igazságának vagy hamisságának meghatározását. Például azt a kijelentést: „Ha öt több mint kettő ( A), akkor a kedd mindig hétfő után jön ( V) "- következmény A→ V, és a művelet eredménye ebben az esetben "igaz". A logikai műveletek során a kijelentések jelentését nem veszik figyelembe, csak azok igazságát vagy hamisságát veszik figyelembe.
Vegyük például egy összetett állítás felépítését az állításokból Aés V ami hamis lenne akkor és csak akkor, ha mindkét állítás igaz. A modulo two összeadás működésének igazságtáblázatában ezt találjuk: 1 ⊕ 1 = 0. És az állítás lehet például ez: "Ez a golyó teljesen piros vagy teljesen kék." Ezért ha az állítás A"Ez a labda teljesen piros" igaz, és a kijelentés V„Ez a labda teljesen kék” igaz, akkor az összetett állítás hazugság, mert a labda nem lehet egyszerre piros és kék.
Példák a problémamegoldásra
1. példa. Határozza meg az X jelzett értékeihez a logikai utasítás értékét ((X> 3) ∨ (X< 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Megoldás. A műveletek sorrendje a következő: először a zárójelben lévő összehasonlító műveleteket hajtják végre, majd a diszjunkciót, és az utolsó az implikációs művelet. A j diszjunkciós művelet akkor és csak akkor hamis, ha mindkét operandus hamis. Az igazságtábla a következményre az
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Innen kapjuk:
1) X = 1 esetén:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) X = 12 esetén:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) X = 3 esetén:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
2. példa. Adja meg az X egész számok azon halmazát, amelyre a ¬ ((X> 2) → (X> 5)) kifejezés igaz.
Megoldás. A tagadási művelet a teljes kifejezésre vonatkozik ((X> 2) → (X> 5)), ezért ha a ¬ ((X> 2) → (X> 5)) kifejezés igaz, akkor az ((X > 2) → (X> 5)) hamis. Ezért meg kell határozni, hogy X mely értékei esetén a ((X> 2) → (X> 5)) hamis. Az implikációs művelet csak egy esetben veszi fel a "false" értéket: amikor az igazságból hamis következik. És ez csak X = 3 esetén történik; X = 4; X = 5.
3. példa. A megadott szavak közül melyik hamis az állítás ¬ (magánhangzó első betűje ∧ magánhangzó harmadik betűje) ⇔ egy 4 karakterből álló karakterlánc? 1) assa; 2) kuku; 3) kukorica; 4) hiba; 5) erős ember.
Megoldás. Tekintsük sorban az összes javasolt szót:
1) a szamár szónál ezt kapjuk: ¬ (1 ∧ 0) ⇔ 1, 1 ⇔ 1 - az állítás igaz;
2) a kuku szóhoz ezt kapjuk: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 - az állítás igaz;
3) a kukorica szónál ezt kapjuk: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 - az állítás hamis;
4) a hiba szóhoz ezt kapjuk: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 - az állítás igaz;
5) az erősember szóhoz ezt kapjuk: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 - az állítás hamis.
Logikai kifejezések és átalakításuk
Alatt logikus kifejezés meg kell értenie egy olyan rekordot, amely logikai értéket vehet fel "igaz" vagy "hamis". Ezzel a definícióval meg kell különböztetni a logikai kifejezéseket:
- kifejezések, amelyek összehasonlítási műveleteket ("nagyobb", "kisebb", "egyenlő", "nem egyenlő" stb.) használnak és logikai értékeket vesznek fel (például az a> b kifejezés, ahol a = 5 és b = 7, egyenlő a "false" értékkel);
- logikai értékekhez és logikai műveletekhez kapcsolódó közvetlen logikai kifejezések (például A ∨ B ∧ C, ahol A = igaz, B = hamis és C = igaz).
A logikai kifejezések tartalmazhatnak függvényeket, algebrai műveleteket, összehasonlító műveleteket és logikai műveleteket. Ebben az esetben a műveletek végrehajtásának prioritása a következő:
- a meglévő funkcionális függőségek kiszámítása;
- algebrai műveletek végrehajtása (először szorzás és osztás, majd kivonás és összeadás);
- összehasonlító műveletek végrehajtása (nem meghatározott sorrendben);
- logikai műveletek végrehajtása (a tagadás kezdeti műveletei, majd a logikai szorzás, logikai összeadás, az utolsó implikációs és ekvivalenciaműveletek végrehajtása).
A logikai kifejezések zárójeleket használhatnak, amelyek megváltoztatják a műveletek végrehajtásának sorrendjét.
Példa. Keresse meg a kifejezés értékét:
$ 1 ≤ a ∨ A ∨ sin (π / a - π / b)< 1 ∧ ¬B ∧ ¬(b^a + a^b >a + b ∨ A ∧ B) $ a = 2, b = 3, A = igaz, B = hamis.
Megoldás. Az értékek számítási sorrendje:
1) b a + a b> a + b, helyettesítés után kapjuk: 3 2 + 2 3> 2 + 3, azaz 17> 2 + 3 = igaz;
2) A ∧ B = igaz ∧ hamis = hamis.
Ezért a zárójelben lévő kifejezés (b a + a b> a + b ∨ A ∧ B) = igaz ∨ hamis = igaz;
3) 1≤ a = 1 ≤ 2 = igaz;
4) bűn (π / a - π / b)< 1 = sin(π/2 - π/3) < 1 = истина.
Ezen számítások után végre megkapjuk: igazság ∨ А ∧ igaz ∧ ¬В ∧ ¬true.
A tagadási műveleteket most végre kell hajtani, amit logikai szorzás és összeadás követ:
5) ¬В = ¬hamis = igaz; ¬igaz = hamis;
6) A ∧ igaz ∧ igaz ∧ hamis = igaz ∧ igaz ∧ igaz ∧ hamis = hamis;
7) igaz ∨ hamis = igaz.
Így egy logikai kifejezés eredménye adott értékek esetén "igaz".
Jegyzet. Figyelembe véve, hogy az eredeti kifejezés végül két tag összege, és egyikük értéke 1 ≤ a = 1 ≤ 2 = igaz, további számítások nélkül azt mondhatjuk, hogy az eredmény a teljes kifejezésre is "igaz".
A logikai kifejezések azonos konverziói
A logika algebrájában teljesülnek az alapvető törvények, amelyek lehetővé teszik a logikai kifejezések azonos átalakításainak végrehajtását.
| Törvény | ∨ számára | ∧ számára |
| Hajtó | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Kombinatív | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Csomópont | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| De Morgan szabályai | $ (A ∨ B) ↖ (-) $ = $ A↖ (-) ∧ B↖ (-) $ | $ (A ∧ B) ↖ (-) $ = $ A↖ (-) ∨ B↖ (-) $ |
| Idempotenciák | A ∨ A = A | A ∧ A = A |
| Abszorpció | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Ragasztás | (A ∧ B) ∨ (A↖ (-) ∧ B) = B | (A ∨ B) ∧ (A↖ (-) ∨ B) = B |
| Változó működés inverziójával | $ A ∨ A↖ (-) $ = 1 | $ A ∧ A↖ (-) $ = 0 |
| Működés konstansokkal | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Kettős tagadás | $ A↖ (=) $ = A | |
Ezen állítások igazolása a megfelelő rekordok igazságtábláinak összeállítása alapján történik.
A logikai képletek egyenértékű transzformációinak ugyanaz a célja, mint a rendes algebrában szereplő képletek transzformációinak. A képletek egyszerűsítésére vagy bizonyos formába hozására szolgálnak a logika algebrájának alaptörvényeinek használatával. Alatt a képlet egyszerűsítése, amely nem tartalmazza az implikációs és egyenértékűségi műveleteket, egyenértékű transzformációként értendő, amely olyan képlethez vezet, amely vagy kevesebbet tartalmaz, mint az eredeti műveletek száma, vagy kevesebb változót.
A logikai képletek bizonyos transzformációi hasonlóak a rendes algebrai képletek transzformációihoz (a közös tényező kivétele a zárójelben, az elmozdulási és kombinációs törvények használata stb.), Míg más transzformációk olyan tulajdonságokon alapulnak, amelyekkel a közönséges algebra műveletei nem rendelkeznek (az elosztási törvény alkalmazásával összefüggésben, az abszorpció, ragasztás törvényei, de Morgan stb.).
Nézzünk példákat néhány logikai képlet egyszerűsítésére használt technikára és módszerre:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2.
Az átalakításhoz itt alkalmazhatja az idempotencia törvényét, az elosztási törvényt; fordított változó művelet és állandó működés.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1.
Itt az egyszerűség kedvéért az abszorpciós törvényt alkalmazzák.
3) ¬ (X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1.
Átalakításkor de Morgan szabálya, egy változó inverzióval való művelete, egy konstans művelet
Példák a problémamegoldásra
1. példa. Keressen A ∧ ¬ (¬B ∨ C) -nek megfelelő Boole -kifejezést.
Megoldás. De Morgan szabályát alkalmazzuk B -re és C -re: ¬ (¬B ∨ C) = B ∧ ¬C.
Az eredetivel egyenértékű kifejezést kapunk: A ∧ ¬ (¬B ∨ C) = A ∧ B ∧ ¬C.
Válasz: A ∧ B ∧ ¬C.
2. példa. Adja meg az A, B, C logikai változók értékét, amelyeknél a (A ∨ B) → (B ∨ ¬C ∨ B) logikai kifejezés értéke hamis.
Megoldás. Az implikáció művelete csak abban az esetben hamis, ha hamisság következik az igaz premisszából. Ezért egy adott kifejezéshez az A ∨ B premisszának fel kell vennie az "igaz" értéket, és a következménynek, azaz a B ∨ ¬C ∨ B kifejezésnek "hamisnak" kell lennie.
1) A ∨ B - a diszjunkció eredménye "igaz", ha legalább az egyik operandus "igaz";
2) B ∨ ¬C ∨ B - a kifejezés hamis, ha minden kifejezés értéke „false”, azaz B - „hamis”; ¬C - "hamis", ezért a C változó értéke "true";
3) Ha figyelembe vesszük az előfeltevést és figyelembe vesszük, hogy B „hamis”, akkor azt kapjuk, hogy A értéke „igaz”.
Válasz: A igaz, B hamis, C az igazság.
3. példa. Melyik a legnagyobb X egész szám, amelyre az állítás (35
Megoldás.Írjuk fel az igazságtáblázatot az implikációs művelethez:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
X kifejezés< (X - 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Válasz: X = 5.
Logikai kifejezések használata a geometriai régiók leírásához
A logikai kifejezések geometriai területek leírására használhatók. Ebben az esetben a feladat a következőképpen fogalmazódik meg: adott geometriai régió esetén írjon le egy logikai kifejezést, amely az "true" értéket veszi fel az x, y értékekre, és csak akkor, ha bármelyik pont koordinátákkal (x; y) a geometriai tartományhoz tartozik.
Tekintsük egy geometriai terület leírását logikai kifejezés segítségével példák segítségével.
1. példa. Egy geometriai terület képe van megadva. Írjon egy logikai kifejezést, amely leírja a hozzá tartozó pontok halmazát.
1)  .
.
Megoldás. Egy adott geometriai régió a következő régiók halmazaként ábrázolható: az első régió - D1 - félsík $ (x) / ( - 1) + (y) / (1) ≤ 1 $, a második - D2 - kör középpontjával $ x ^ 2 + y ^ 2 ≤ 1 $. D1 $ ∩ $ D2 metszéspontjuk a kívánt tartomány.

Eredmény: logikai kifejezés $ (x) / (- 1) + (y) / (1) ≤ 1 ∧ x ^ 2 + y ^ 2 ≤ 1 $.
2) 
Ez a terület így írható: | x | ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1.
Jegyzet. A logikai kifejezés megalkotásakor gyenge egyenlőtlenségeket használnak, ami azt jelenti, hogy az ábrák határai is az árnyékolt területhez tartoznak. Ha szigorú egyenlőtlenségeket alkalmaznak, akkor a határokat nem veszik figyelembe. A régióhoz nem tartozó szegélyeket általában szaggatott vonallal jelölik.
Megoldhatja az inverz feladatot, nevezetesen: rajzoljon egy területet egy adott logikai kifejezéshez.
2. példa. Rajzoljon és árnyékoljon egy területet, amelynek pontjaira a logikai feltétel teljesül y ≥ x ∧ y + x ≥ 0 ∧ y< 2 .
Megoldás. A kívánt régió három félsík metszéspontja. Az (x, y) síkra építünk y = x; y = -x; y = 2. Ezek a terület határai, és az utolsó y = 2 határ nem tartozik a területhez, ezért szaggatott vonallal rajzoljuk meg. Az y ≥ x egyenlőtlenség teljesítéséhez szükséges, hogy a pontok az y = x egyenestől balra legyenek, és az y = -x egyenlőtlenség teljesüljön azoknál a pontoknál, amelyek az y = -x egyenestől jobbra vannak. Feltétel y< 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:

Logikai függvények használata az elektromos áramkörök leírására
A logikai funkciók nagyon hasznosak az elektromos áramkörök működésének leírásához. Tehát az ábrán látható áramkör esetében, ahol az X változó értéke a kapcsoló állapota (ha be van kapcsolva, akkor X értéke "igaz", és ha kikapcsolt, akkor "hamis") , ez az Y érték az izzó állapota (ha be van kapcsolva - az érték "igaz", és ha nem - "hamis"), akkor a logikai függvény a következőképpen íródik fel: Y = X. Az Y függvényt hívják a vezetőképesség funkciója.

Az ábrán látható áramkör esetében az Y logikai függvény a következő formában jelenik meg: Y = X1 ∪ X2, mivel egy bekapcsolt kapcsoló elegendő a fény égéséhez. Az ábrán látható diagramon, Ahhoz, hogy a fény égjen, mindkét kapcsolót be kell kapcsolni, ezért a vezetőképesség függvény a következő alakú: Y = X1 ∧ X2.

Egy összetettebb áramkör esetén a vezetőképesség függvény a következő lesz: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).

Az áramkör záróérintkezőket is tartalmazhat. Ebben az esetben a nyitott érintkező, mint kapcsoló biztosítja, hogy a lámpa a gomb elengedésekor felgyulladjon, és ne nyomja meg. Az ilyen áramköröknél a leválasztó kapcsolót a tagadás írja le.
A két sémát ún egyenértékű ha az áram átmegy az egyiken, amikor a másikon is. A két egyenértékű áramkör közül az egyszerűbb az az áramkör, amelynek vezetőképesség -függvénye kevesebb elemet tartalmaz. Nagyon fontos az a feladat, hogy megtaláljuk a legegyszerűbb sémákat az egyenértékűek között.
A logikai algebra apparátusának használata a logikai áramkörök tervezésében
A logikai matematika algebrája nagyon praktikus a számítógépes hardver működésének leírásához. A számítógépen történő feldolgozás során minden információt bináris formában ábrázolnak, vagyis valamilyen 0 és 1 sorozat kódolja. A 0 -nak és 1 -nek megfelelő bináris jelek feldolgozását a számítógépen logikai elemek végzik. Logikai kapuk, amelyek alapvető logikai műveleteket végeznek ÉS VAGY NEM,ábrán láthatók.

A logikai elemek szimbólumai szabványosak, és a számítógép logikai áramköreinek összeállításakor használatosak. Ezen áramkörök használatával bármilyen logikai függvényt megvalósíthat, amely leírja a számítógép működését.
Technikailag a számítógépes logikai elemet elektromos áramkör formájában valósítják meg, amely különböző részek összeköttetése: diódák, tranzisztorok, ellenállások, kondenzátorok. A logikai elem bemenete, amelyet kapunak is neveznek, magas és alacsony feszültségű elektromos jeleket fogad, és egy kimeneti jel is adódik, akár magas, akár alacsony, a kimeneten. Ezek a szintek a bináris rendszer egyik állapotának felelnek meg: 1 - 0; IGAZ HAMIS. Minden logikai elemnek saját szimbóluma van, amely logikai funkcióját fejezi ki, de nem jelzi, hogy milyen elektronikus áramkört valósítanak meg benne. Ez megkönnyíti az összetett logikai áramkörök írását és megértését. A logikai áramkörök működését igazságtáblázatok segítségével írják le. Hagyományos jelölés a VAGY áramkörön, az "1" jel - a diszjunkció elavult megjelöléséből "> = 1" (a diszjunkció értéke 1, ha a két operandus összege nagyobb vagy egyenlő 1 -el). Az ÉS diagram "&" jele az angol szó rövidítése.
Az elektronikus logikai áramkörök logikai elemekből állnak, amelyek bonyolultabb logikai műveleteket végeznek. A NOT, OR és AND elemekből álló logikai elemek halmazát, amelynek segítségével bármilyen összetettségű logikai struktúrát felépíthet, ún. funkcionálisan teljes.
Logikai kifejezési igazságtáblázatok készítése
A logikai képlethez mindig írhat igazság táblázat, vagyis egy adott logikai függvényt ábrázolni táblázatos formában. Ebben az esetben a táblázatnak tartalmaznia kell a függvény argumentumok (képletek) és a megfelelő függvényértékek (képleteredmények adott értékkészleten) minden lehetséges kombinációját.
A függvény értékeinek megkeresésének kényelmes formája a táblázat, amely a változók és a függvényértékek mellett a köztes számítások értékeit is tartalmazza. Tekintsünk egy példát igazságtábla készítésére a $ (X1) ↖ (-) ∧ X2 ∨ (X1 ∨ X2) ↖ (-) ∨ X1 $ képlethez.
| X1 | X2 | $ (X1) ↖ (-) $ | $ (X1) ↖ (-) $ \ X2 | X1 ∧ X2 | $ (X1 ∨ X2) ↖ (-) $ | $ (X1) ↖ (-) $ ∧ X2 ∨ $ (X1 ∨ X2) ↖ (-) $ | $ (X1) ↖ (-) $ ∧ X2 ∨ $ (X1 ∨ X2) ↖ (-) $ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Ha egy függvény minden változóérték -készlethez az 1 -es értéket veszi fel, akkor az egyformán igaz; ha a bemeneti értékek minden halmazánál a függvény 0 értéket vesz fel, akkor az azonos módon hamis; ha a kimeneti értékek halmaza 0 -t és 1 -et is tartalmaz, akkor a függvény meghívásra kerül megvalósítható... A fenti példa egy példát mutat egy azonos funkcióra.
A logikai függvény elemzési formájának ismeretében bármikor eljuthat a logikai függvények táblázatos formájához. Egy adott igazságtáblázat segítségével megoldható az inverz probléma, nevezetesen: egy adott táblázathoz készítsünk analitikai képletet egy logikai függvényhez. A logikai függvény analitikai függőségének egy adott táblázatfüggvény szerinti kialakításának két formája létezik.
1. Diszjunktív normál forma (DNF)- a változókból képzett termékek összege és azok hamis értékekre vonatkozó tagadásai.
A DNF felépítésének algoritmusa a következő:
- a függvény igazságtáblázatában olyan argumentumhalmazok vannak kiválasztva, amelyek logikai alakjai 1 -el ("igaz") egyenlők;
- az összes kiválasztott logikai halmazt argumentumok logikai termékeiként írjuk le, és egy logikai összeg (diszjunkció) működésével egymás után összekötjük őket;
- hamis argumentumok esetén a tagadási műveletet alkalmazzák a felépített rekordra.
Példa. A DNF metódus segítségével hozzon létre egy függvényt, amely meghatározza, hogy az első szám megegyezik a második számmal. A függvény igazságtáblázatának formája van
| X1 | X2 | F (X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Megoldás. Kiválasztjuk azokat az argumentumérték -halmazokat, amelyekben a függvény értéke 1. Ezek a táblázat első és negyedik sora (a fejléc sorszámozásakor nem veszik figyelembe).
E halmazok argumentumainak logikai szorzatait írjuk le, összekapcsolva egy logikai összeggel: X1 ∧ X2 ∨ X1 ∧ X2.
A tagadást a kijelölt halmazok hamis értékű argumentumaira írjuk (a táblázat negyedik sora; a képlet második halmaza; az első és a második elem): X1 ∧ X2 ∨ $ (X1) ↖ ( -) $ ∧ $ (X2) ↖ (-) $.
Válasz: F (X1, X2) = X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ $ (X2) ↖ (-) $.
2. Konjunktív normál forma (CNF)- a változókból képzett összegek szorzata és azok valódi értékekre vonatkozó tagadásai.
A CNF felépítésének algoritmusa a következő:
- az igazságtáblázatban olyan argumentumkészleteket választanak ki, amelyek logikai formái 0 -val ("hamis");
- az összes kiválasztott logikai halmaz, mint logikai argumentumösszeg, sorrendben íródik, összekapcsolva őket egy logikai termék (kötőszó) működésével;
- igaz argumentumok esetén a tagadási műveletet a konstruált rekord rögzíti.
Példák a problémamegoldásra
1. példa. Tekintsük az előző példát, vagyis a CNF módszerrel készítsünk olyan függvényt, amely meghatározza, hogy az első szám egyenlő a másodikkal. Egy adott függvényhez az igazságtáblázat formája
| X1 | X2 | F (X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Megoldás. Olyan argumentumérték -halmazokat választunk ki, amelyekben a függvény egyenlő 0. Ezek a második és a harmadik sor (a címsort nem veszik figyelembe számozáskor).
E halmazok argumentumainak logikai összegeit írjuk le, egy logikai szorzattal kombinálva: X1 ∨ X2 ∧ X1 ∨ X2.
A tagadást a kijelölt halmazok igaz értékű argumentumaira írjuk (a táblázat második sora, a képlet első halmaza, a második elem; a harmadik sor esetében ez a képlet második halmaza , az első elem): X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2.
Így rekordot kaptunk a CNF logikai függvényéről.
Válasz: X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2.
A két módszerrel kapott függvényértékek egyenértékűek. Ennek az állításnak a bizonyítására a logikai szabályokat használjuk: F (X1, X2) = X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2 = X1 ∧ $ (X1) ↖ (-) $ ∨ X1 ∧ X2 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ $ (X2) ↖ (-) $ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $ (X2 ) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ 0 = X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ $ (X2) ↖ (-) $.
2. példa... Konstruáljon logikai függvényt egy adott igazságtáblához:
A keresett képlet: X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ X2.
Egyszerűsíthető: X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ X2 = X2 ∧ (X1 ∨ $ (X1) ↖ (-) $) = X2 ∧ 1 = X2.
3. példa. Az adott igazságtáblázathoz készítsen logikai függvényt a DNF módszerrel.
| X1 | X2 | X3 | F (X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | X1, X2, X3 | |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | $ (X1) ↖ (-) $ ∧ X2 ∧ X3 | |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | X1 ∧ X2 ∧ $ (X3) ↖ (-) $ | |
| 1 | 0 | 0 | 1 | X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $ | |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
A keresett képlet: X1 ∧ X2 ∧ X ∨ $ (X1) ↖ (-) $ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $ (X3) ↖ (-) $ ∪ X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $.
A képlet meglehetősen nehézkes, és egyszerűsíteni kell:
X1 ∧ X2 ∧ X3 ∨ $ (X1) ↖ (-) $ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $ (X3) ↖ (-) $ ∨ X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $ = X2 ∧ X3 ∧ (X1 ∨ $ (X1) ↖ (-) $) 1 X1 ∧ $ (X3) ↖ (-) $ ∧ (X2 ∨ $ (X2) ↖ (-) $) = X2 ∧ X3 ∨ X1 ∧ $ (X3) ↖ (-) $.
Igazságtáblák a logikai problémák megoldásához
Az igazságtáblázatok összeállítása a logikai problémák megoldásának egyik módja. Ennek a megoldásnak a használatakor a probléma által előírt feltételeket rögzítik a speciálisan összeállított táblázatok segítségével.
Példák a problémamegoldásra
1. példa. Hozzon létre egy igazságtáblázatot egy biztonsági érzékelőhöz, amely három érzékelőt használ, és akkor aktiválódik, ha csak kettő zárva van.
Megoldás. Nyilvánvaló, hogy a megoldás egy táblázatot eredményez, amelyben a kívánt Y (X1, X2, X3) függvény értéke "true" lesz, ha bármelyik két változó értéke "true".
| X1 | X2 | X3 | Y (X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
2. példa. Hozzon létre egy napi órarendet, figyelembe véve, hogy egy informatika óra csak az első vagy a második lehet, a matematika - az első vagy a harmadik, a fizika - a második vagy a harmadik. Lehet -e olyan ütemtervet készíteni, amely minden követelménynek megfelel? Hány ütemezési lehetőség van?
Megoldás. A probléma könnyen megoldható, ha elkészíti a megfelelő táblázatot:
| 1. lecke | 2. lecke | 3. lecke | |
| Számítástechnika | 1 | 1 | 0 |
| Matematika | 1 | 0 | 1 |
| Fizika | 0 | 1 | 1 |
A táblázat azt mutatja, hogy a kívánt ütemezésnek két lehetősége van:
- matematika, informatika, fizika;
- informatika, fizika, matematika.
3. példa. Három barát érkezett a sporttáborba - Peter, Boris és Alexey. Mindegyikük két sportot szeret. Ismeretes, hogy hat ilyen sportág létezik: foci, jégkorong, síelés, úszás, tenisz, tollaslabda. Az is ismert, hogy:
- Borisz a legidősebb;
- aki focizik, fiatalabb, mint a jégkorongozó;
- focizni és jégkorongozni, Péter pedig ugyanabban a házban él;
- amikor veszekedés támad egy síelő és egy teniszező között, Borisz megbékíti őket;
- Péter nem tud teniszezni vagy tollaslabdázni.
Milyen sportokat szeretnek a fiúk?
Megoldás.Állítsunk össze egy táblázatot, és tükrözzük benne a probléma feltételeit, töltsük ki a megfelelő cellákat 0 és 1 számokkal, attól függően, hogy a megfelelő állítás hamis vagy igaz.
Mivel hatféle sport létezik, kiderül, hogy minden fiú szereti a különböző sportokat.
A 4. feltételből következik, hogy Borisz nem szeret síelni vagy teniszezni, de a 3. és 5. feltételből azt, hogy Péter nem tud focizni, hokizni, teniszezni és tollaslabdázni. Ezért Péter kedvenc sportjai a síelés és az úszás. Írjuk be ezt a táblázatba, és a "Sí" és "Úszás" oszlopok többi celláját töltsük ki nullával.
A táblázat azt mutatja, hogy csak Alekszej tud teniszezni.
Az 1. és 2. feltételből következik, hogy Borisz nem futballista. Így Alexey focizik. Folytassuk a táblázat kitöltését. Írjuk be a nullákat az "Alexey" sor üres celláiba.
Végül meglátjuk, hogy Borisz szereti a jégkorongot és a tollaslabdát. A döntő asztal így fog kinézni:
Válasz: Peter szeret síelni és úszni, Boris hokizik és tollaslabdázik, Alexey pedig focizik és teniszezik.
1. feladat # 10050
\ ((x \ ék y) \ vee (x \ ék \ overline y) \ vee (y \ ék z) \ vee (z \ ék x) \)
Készíts neki igazságtáblázatot. A válaszhoz adja meg a \ ((x, \) \ (y, \) \ (z), \) halmazok számát, amelyekhez a függvény 1.
1. Egyszerűsítse \ ((x \ ék y) \ vee (x \ ék \ overline y). \)
Az elosztási törvény szerint \ ((y \ ék x) \ vee (x \ ék \ overline y) \) = \ (x \ ék (y \ vee \ overline y). \)\ (y \ vee \ overline y = 1 \) (ha \ (y = 0, \) akkor \ (\ overline y \ vee y = 1 \ vee 0 = 1, \) ha \ (y = 1, \) akkor \ (\ overline y \ vee y = 0 \ vee 1 = 1). \) Azután \ (x \ ék (y \ vee \ overline y) = x \ ék 1 = x. \)
2. Egyszerűsítse \ ((y \ ék z) \ vee (z \ ék x). \) Az elosztási törvény szerint \ ((y \ ék z) \ vee (z \ ék x) = z \ ék (y \ vee x). \)
3. Kapjuk: \ ((x \ ék y) \ vee (x \ ék \ overline y) \ vee (y \ ék z) \ vee (z \ ék x) = x \ vee z \ ék (y \ vee x). \)
4. Az igazságtábla 8 sort tartalmaz (a sorok mindig \ (2 ^ n, \) ahol \ (n \) a változók száma). Esetünkben 3 változó létezik.
5. Töltse ki az igazság táblázatot.
\ [\ begin (tömb) (| c | c | c | c | c | c | c |) \ hline x & y & z & y \ vee x & z \ ék (y \ vee x) & F = x \ vee z \ ék (y \ vee x) \\ \ hline 0 & 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 & 0 & 0 \\ \ hline 0 & 1 & 0 & 1 & 0 & 0 \\ \ hline 0 & 1 & 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 1 & 0 & 1 \\ \ hline 1 & 0 & 1 & 1 & 1 & 1 \\ \ hline 1 & 1 & 0 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 1 & 1 & 1 \\ \ hline \ end (tömb) \]
A szétválás óta \ (x \ vee z \ ék (y \ vee x) \) igaz, ha a benne szereplő állítások közül legalább az egyik igaz, akkor \ (x = 1 \) \ (F = 1 \) esetén bármely \ (y \) és \ (z \) esetén (5-8. az igazságtáblázat).
Tekintsük azt az esetet, amikor \ (x = 0. \) Ekkor a függvény értéke függ a \ (z \ ék (y \ vee x) értékétől. \) Ha \ (z \ ék (y \ vee x) \ ) igaz, akkor és \ (F \) igaz, ha hamis, akkor az \ (F \) hamis. Tekintsük azt az esetet, amikor \ (F = 1. \) A \ ((z \ ék (y \ vee x)) \) kötőszó igaz, ha a benne szereplő összes állítás igaz, azaz \ (y \ vee x = 1 \) és \ (z = 1. \) \ (x = 0, \) azt jelenti: \ (y \ vee x = 1, \), amikor \ (y = 1 \) (4. sor).
Ha a kötőszóban szereplő egyik állítás hamis, akkor az egész kötőszó hamis. Ha \ (x = 0 \) és \ (y = 0, \) akkor \ (y \ vee x = 0. \) Akkor \ (z \ ék (x \ vee y) = 0 \) bármely \ (z \) (1-2. sor). Mivel a \ (x = 0, \) és a \ ((z \ wedge (x \ vee y)), \) diszjunkció második állítása is hamis, akkor az egész függvény hamis. Ha \ (x = 0 \) és \ (y = 1, \) akkor \ (y \ vee x = 1. \) Ha \ (z = 0, \) \ (z \ ék (y \ vee x) = 0. \) Ezután \ (F = 0 \) (3. sor). Az az eset, amikor a \ (z = 1, \) \ (y = 1, \) \ (x = 0, \) az előző bekezdésben került figyelembevételre.
Építettünk egy igazságtáblát. Látjuk, hogy 5 halmaz van benne, amelyekre \ (F = 1. \) Ezért a válasz 5.
Válasz: 5
2. küldetés # 10051
A \ (F \) logikai függvényt a következő kifejezés adja:
\ ((x \ ék \ overline y \ ék z) \ vee (x \ jobbra mutató y) \)
Készíts neki igazságtáblázatot. A válaszhoz adja meg azon \ ((x, \) \ (y, \) \ (z), \) halmazok számát, amelyeknél a függvény 0.
\ [\ begin (tömb) (| c | c | c | c | c | c | c | c | c |) \ hline x & y & z & \ overline y & x \ wedge \ overline y & x \ wedge \ overline y \ ék z & \ overline x & \ overline x \ vee y & x \ wedge \ overline y \ wedge z \ vee \ overline x \ vee y \\ \ hline 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ \ hline 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 és 1 \\ \ hline \ end (tömb) \]
1. \ (x \ jobbra nyíl y \) = \ (\ overline x \ vee y. \)
2. Vegye figyelembe, hogy \ (y = 1 \) \ (F = 1, \) esetén, mivel a diszjunkció igaz, ha legalább egy benne szereplő kifejezés igaz (3-4., 7-8. Sor az igazságtáblázatban). Hasonlóképpen \ (\ overline x = 1, \) esetén, azaz \ (x = 0, \) \ (F = 1 \) esetén (1-4. Sor).
3. \ (x = 1 \) és \ (y = 0 \) \ (\ overline x \ vee y = 0, \) \ (x \ wedge \ overline y = 1.) esetén \ (z = 1 \) \ (x \ ék \ overline y \ ék z = 1 \)és \ (F = 1, \), mivel az egyik kifejezés (6. sor) igaz, és \ (z = 0 \) esetén \ (x \ ék \ overline y \ ék z = 0 \)és \ (F = 0, \), mivel a diszjunkcióban szereplő mindkét kifejezés hamis (5. sor).
A felépített igazságtábla szerint azt látjuk, hogy egy halmazra \ ((x, \) \ (y, \) \ (z) \) \ (F = 0. \)
Válasz: 1
3. feladat # 10052
A \ (F \) logikai függvényt a következő kifejezés adja:
\ ((\ overline (z \ vee \ overline y)) \ vee (w \ wedge (z \ equiv y)) \)
Készíts neki igazságtáblázatot. Válaszként adja meg a \ (z, \) \ (y \) és \ (w, \) értékek összegét, amelyekhez \ (F = 1. \)
\ [\ begin (tömb) (| c | c | c | c | c | c | c | c | c |) \ hline w & y & z & \ overline y & z \ vee \ overline y & \ overline ( z \ vee \ overline y) & z \ equiv y & w \ wedge (z \ equiv y) & \ overline z \ vee \ overline y \ vee w \ wedge (z \ equiv y) \\ \ hline 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ \ hline 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \ hline 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ \ hline 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 \\ \ hline \ end (tömb) \]
1. \ ((\ overline (z \ vee \ overline y)) = \ overline z \ y ék \]
2. Az igazságtábla \ (2 ^ 3 = 8 \) sorokat tartalmaz.
3. Ha \ (z = 1 \) és \ (y = 1, \) \ (akkor (z \ equiv y) = 1 \) (mivel az egyenérték akkor és csak akkor igaz, ha mindkét állítás egyszerre hamis vagy igaz) ... \ (\ overline z \ ék y = 0 \) \ ((0 \ ék 1 = 0). \) Ha \ (w = 1, \) \ (w \ ék (z \ ekvivalens) = 1 \) \ ((1 \ ék 1 = 1) \) és \ (F = 1, \), mivel a diszjunkció igaz, ha a benne foglalt állítások közül legalább az egyik igaz (az igazságtábla 8. sora). Ha \ (w = 0, \) \ (w \ ék (z \ equiv y) = 0 \) \ ((0 \ ék 1 = 0) \) és \ (F = 0, \), mivel mindkét állítás tartalmazza a diszjunkcióban hamisak (4. sor).
4. Hasonlóan a \ (z = 0, y = 0. \) \ ((z \ equiv y) = 1, \) \ (\ overline z \ ék y = 0 \) \ ((1 \ ék 0 = 0 ). \) Ezután a függvény értéke ismét függ a \ (w. \) -Tól \ (w = 1 \) \ (w \ ék (z \ equiv y) = 1, \)\ (F = 1, \) mivel a diszjunkcióban szereplő egyik állítás igaz (5. sor), és \ (w = 0 \) esetén \ (w \ ék (z \ equiv y) = 0, \)\ (F = 0, \), mivel minden állítás hamis (1. sor).
5. Ha \ (z = 0 \) és \ (y = 1, \) akkor \ (\ overline z \ ék y = 1 \) \ ((1 \ ék 1 = 1). \) Mivel \ ((z \ equiv y) = 0 \) (elvégre a \ (z \) és \ (y \) értékek eltérnek), hamisak lesznek minden \ (w. \) esetén, mivel a változó értéke \ (w \) nem befolyásolja a függvény értékét, mert \ (z = 0 \) és \ (y = 1 \) \ (w \) lehet 0 vagy 1. \ (F = 1, \ ), mivel a diszjunkcióban szereplő egyik állítás igaz, (3., 7. sor).
6. Ha \ (z = 1 \) és \ (y = 0, \) akkor \ (\ overline z \ ék y = 0 \ ék 0 = 0. \) Mivel \ ((z \ equiv y) = 0, \) \ (w \ ék (z \ equiv y) = w \ ék 0 \) hamis lesz minden \ (w \) esetén (azaz \ (w \) lehet 0 és 1). Ezért a \ (z = 1 \) és \ (y = 0 \) \ (F \) esetén mindig hamis lesz (mivel a diszjunkcióban szereplő mindkét állítás hamis, 2., 5. sor).
7. \ (F = 1 \) a következő halmazokhoz \ (z, \) \ (y, \) \ (w: \) (0, 0, 1), (0, 1, 1), (1, 1, 1), (0, 1, 0). Ha összeadjuk az értékeket, akkor 7 -et kapunk.
Válasz: 7
4. feladat # 10053
A \ (F \) logikai függvényt a következő kifejezés adja:
\ (a \ ék ((\ overline (b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a)) \)
Készíts neki igazságtáblázatot. Válaszként adja meg a \ (a, \) \ (b \) és \ (c, \) értékek összegét, amelyekhez \ (F = 1. \)
\ [\ begin (tömb) (| c | c | c | c |) \ hline a & b & c & F \\\ hline 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 \ \ \ hline 0 & 1 & 0 & 0 \\ \ hline 0 & 1 & 1 & 0 \\ \ hline 1 & 0 & 0 & 1 \\ \ hline 1 & 0 & 1 & 1 \\ \ hline 1 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 \\ \ hline \ end (tömb) \]
1. Az igazságtáblázat \ (2 ^ 3 = 8 \) soraiban.
2. \ (a = 0 \) \ (F = 0 \) esetén minden értékre \ (b \) és \ (c, \), mivel a kötőszó akkor és csak akkor igaz, ha a benne szereplő összes állítás igaz (1-4. sorok az igazságtáblázatban).
3. Tekintsük azokat az eseteket, amikor \ (a = 1. \) Ha \ (\ overline ((b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a) = 1, \) akkor \ (F = 1 \) (mivel mindkét állítás igaz lesz), ellenkező esetben \ (F = 0 \) (mivel az egyik állítás hamis lesz). De Morgan törvénye \ (\ overline (b \ wedge c) = \ overline b \ vee \ overline c. \) Ezután, figyelembe véve, hogy \ (a = 1, \) \ (\ overline ((b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a) = \ overline b \ vee \ overline c \ vee \ overline b \ vee \ overline c = \ overline b \ vee \ overline c. \)
4. Ha \ (\ overline b = 0 \) és \ (\ overline c = 0 \) (egyidejűleg, azaz \ (b = 1 \) és \ (c = 1) esetén \), akkor \ (\ overline b \ vee \ overline c = 0 \)és \ (F = 0 \) (8. sor). Más esetekben \ (\ overline b \ vee \ overline c = 1 \)és \ (F = 1 \) (5-7. sor).
5. Azok a \ ((x, \) \ (y, \) \ (z), \) halmazok, amelyekhez \ (F = 1: \) (1, 0, 0), (1, 1, 0), (1, 0, 1). Az értékek összege 5.
Válasz: 5
5. feladat # 10054
A \ (F \) logikai függvényt a következő kifejezés adja:
\ (((a \ ék b) \ vee (b \ c ék)
Készítsen igazságtáblázatot! Válaszként adja meg a \ (a, \) értékek összegét, amelynél \ (F = 0. \)
\ [\ begin (tömb) (| c | c | c | c | c |) \ hline a & b & c & d & F \\\ hline 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 0 & 1 & 1 \\ \ hline 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 1 & 0 \\ \ hline 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 & 0 \\ \ hline 1 & 1 & 0 & 1 & 1 \\ \ hline 1 & 0 & 1 & 0 & 0 \\ \ hline 1 & 0 & 0 & 1 & 0 \\ \ hline 0 & 1 & 1 & 0 & 1 \\ \ hline 1 & 0 & 1 & 1 & 0 \\ \ hline 0 & 1 & 0 & 1 & 0 \\ \ hline \ end (tömb) \]
1. Az elosztási törvény szerint \ ((a \ ék b) \ vee (b \ ék c) = b \ ék (a \ vee c). \)
2. \ (d \ jobb nyíl a = \ overline d \ vee a. \)
3. \ ({ (\ overline d \ vee a \ vee (b \ wedge \ overline c)). \)
4. Ha \ (b = 0, \), akkor a függvény bal oldala 0 \ ((0 \ ék (a \ vee c) = 0). \) \ (b \ ék \ overline c = 0 \ ék \ overline c = 0. \) Ez azt jelenti, hogy \ (b = 0 \) \ (c \) esetén bármi lehet, mivel ez nem befolyásolja a függvény értékét. \ (F = 1, \), ha \ (\ overline d \ vee a = 0 \) (akkor a diszjunkcióban szereplő kifejezések egyike igaz lesz). Ez a \ (\ overline d = 0 \) \ ((d = 1) \) és \ (a = 0 \) (2., 3. sor) segítségével történik. Más \ (d \) és \ (a \) \ (\ overline d \ vee a = 0, \) esetén ez \ (F = 0, \), mivel az egyenértékűségi művelet akkor és csak akkor igaz, ha mindkét utasítás egyidejű igaz vagy hamis (1., 10. sor az igazságtáblázatban).
5. Ha \ (b = 1, \) akkor \ (b \ ék (a \ vee c) = 1 \ ék (a \ vee c) = a \ vee c. \) \ (b \ ék \ overline c = 1 \ ék \ overline c = \ overline c. \) Akkor ez van nálunk \ (a \ vee c \ equiv \ overline d \ vee a \ vee \ overline c. \) Ha \ (a = 1, \) akkor \ (a \ vee c = 1 \) és \ (\ overline d \ vee a \ vee \ overline c = 1, \) mivel a diszjunkció igaz, ha a kifejezések közül legalább az egyik igaz (és mindkét szétválás tartalmaz \ (a = 1). \) Ezután, ha \ (b = 1 \) és \ (a = 1, \) \ (F = 1 \) bármely \ (c \) és \ (d \) esetén (5., 7., 8., 11. sor).
Ha \ (a = 0, \) akkor \ (a \ vee c = 0 \ vee c = c, \) és \ (\ overline d \ vee a \ vee \ overline c = \ overline d \ vee \ overline c. \) Nekünk van: \ (c \ equiv (\ overline d \ vee \ overline c). \)\ (C = 1 \) \ (1 \ equiv \ overline d. \) Esetén \ (d = 1 \) \ (F = 0, \) esetén, mivel az utasítások eltérnek (4. sor), \ (d = 0 \) \ (F = 1, \), mivel mindkét állítás igaz (14. sor). \ (C = 0 \) esetén \ (0 \ equiv (\ overline d \ vee 1). \) Mivel a \ (\ overline d \ vee 1 \) diszjunkció, amelyben az egyik állítás igaz, az egész diszjunkció igaz. Ekkor \ (0 \ ekv. 1, \), ami nem igaz, ami \ (F = 0 \) -t jelent bármely \ (d \) esetén (9., 16. sor).
A felépített táblázat szerint azt látjuk, hogy \ (F = 0 \) \ (a = 0 \) (1., 4., 9., 10., 16. sor) és \ (a = 1 \) esetén (6., 12. sor) , 13, 15). Ekkor az értékek összege 0 * 5 + 1 * 4 = 4.
Válasz: 4
6. feladat # 10055
A \ (F \) logikai függvényt a következő kifejezés adja:
\ ((a \ equiv (b \ vee \ overline c)) \ rightarrow (c \ ék (b \ vee a)) \)
Készítsen igazságtáblázatot! Válaszként adja meg a \ (c, \) értékek összegét, amelyekhez \ (F = 1. \)
\ [\ begin (tömb) (| c | c | c | c |) \ hline a & b & c & F \\\ hline 0 & 0 & 0 & 1 \\ \ hline 0 & 0 & 1 & 0 \ \ \ hline 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 1 \\ \ hline 1 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 \\ \ hline 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 1 \\ \ hline \ end (tömb) \]
A táblázat \ (2 ^ 3 = 8 \) sort tartalmaz.
1. Egy implikáció hamis, ha és csak akkor, ha a hamis egy igaz állításból következik. Ezért \ (F = 0, \), ha a \ (c \ ék (b \ vee a) = 0. \) Más esetekben \ (F = 1. \) Fontolja meg, hogy milyen értékekre \ (a, \ ) \ (b \) és \ (c \) \ (a \ equiv (b \ vee \ overline c) = 1 \)(ha \ (a \ equiv (b \ vee \ overline c) = 0, \) majd \ (F = 1 \) bármely érték esetén \ (c \ ék (b \ vee a) = 0). \)
Ha \ (a = 0, \), akkor végre kell hajtani \ (a \ equiv (b \ vee \ overline c) = 1, \) szükséges \ (b \ vee \ overline c = 0 \) (elvégre az ekvivalenciaművelet akkor és csak akkor igaz, ha mindkét állítás igaz vagy mindkettő hamis). Ahhoz, hogy a \ ((b \ vee \ overline c) \) diszjunkció hamis legyen, mindkét benne szereplő utasításnak hamisnak kell lennie, azaz \ (b = 0 \) és \ (\ overline c = 0 \) \ ( (c = 1). \) Ilyen értékekre \ (c \ ék (b \ vee a) = 1 \ ék (0 \ vee 0) = 0. \) Azután \ ((a \ equiv (b \ vee \ overline c)) \ rightarrow (c \ wedge (b \ vee a)) = 1 \ rightarrow 0 = 0, \)\ (F = 0. \) Ez az igazságtábla 2. sorának felel meg.
Ha \ (a = 1, \), akkor végre kell hajtani \ (a \ equiv (b \ vee \ overline c) = 1, \)\ (b \ vee \ overline c = 1. \) Ez több esetben történik. Ha \ (b = 1, \), akkor a \ (c \) egyenlő lehet nullával és eggyel is, mert a diszjunkcióban szereplő egyik állítás már igaz. \ (C = 1 \) esetén \ (c \ ék (b \ vee a) = 1 \ ék 1 = 1, \) majd \ (F = 1 \) (mivel \ (1 \ jobbra mutató nyíl 1 = 1, \) 7. sor). \ (C = 0 \) esetén \ (c \ ék (b \ vee a) = 0 \ ék 1 = 0, \) ezért \ (F = 0 \) \ ((1 \ jobbra mutató 0 = 0, \) 6. sor). Ha \ (b = 0, \) akkor \ (\ overline c = 1 \) \ ((c = 0, \), akkor a diszjunkcióban szereplő egyik állítás igaz lesz). Ebben az esetben \ (c \ ék (b \ vee a) = 0 \ ék (0 \ vee 1) = 0. \)\ (F = 0, \) óta \ (1 \ jobbra mutató 0 = 0 \) (5. sor).
2. Más értékek \ (a, \) \ (b \) és \ (c \) \ (F = 1, \) miatt \ (a \ equiv (b \ vee \ overline c) = 0 \)(1., 3., 7., 8. sor).
3. Az összeállított igazságtáblázatból azt látjuk, hogy \ (F = 1 \) \ (c = 0 \) (1., 4. sor) és \ (c = 1 \) esetén (3., 7., 8. sor). Az értékek összege 0 * 2 + 1 * 3 = 3. \ (2 ^ 4 = 16 \) sor.
1. Mivel a kötőszó hamis, ha legalább az egyik állítás hamis, akkor \ (d = 0 \) \ (F = 0 \) esetén bármely \ (a, \) \ (b \) és \ ( c \) (az igazságtáblázat 1., 6-10., 12., 14. sora).
2. Tekintsük azt az esetet, amikor \ (d = 1. \) Ekkor \ ((a \ jobbra mutató b) \ ék (b \ ekvivalens c) \ ék d = (a \ jobbra mutató b) \ ék (b \ ekvivalens c) \ ék 1 = (a \ jobbra mutató b) \ ék (b \ ekv c). \)\ (B = 1 \) esetén \ (a \ jobbra nyíl b = a \ jobbra mutató nyíl 1 = 1 \) bármely \ (a, \) esetében, mivel az implikáció hamis akkor és csak akkor, ha a hamis egy igaz állításból következik. Ha \ (c = 1, \) akkor \ (b \ ekvivalens c = 1, \) mivel az egyenértékűségi művelet igaz, ha mindkét kifejezés igaz vagy mindkettő hamis, és \ (F = 1 \) (mivel az összes kifejezés benne van összefüggésben igazak). Ez megfelel a 4. és 5. sornak. Ha \ (c = 0, \) akkor \ (b \ ekvivalens c = 0, \) \ (F = 0, \), mivel a kötőszóban szereplő egyik kifejezés hamis 11. és 16.).
\ (B = 0: \) esetén, ha \ (a = 1, \) akkor \ (a \ jobbra nyíl b = 1 \ jobbra mutató 0 = 0, \) akkor a kötőszóban szereplő egyik kifejezés hamis, és \ (F = 0 \) bármely \ (c \) esetén (13. és 15. sor). Ha \ (a = 0, \) akkor \ (a \ jobbra nyíl b = 0 \ jobbra mutató nyíl 0 = 1. \) Ha \ (c = 0, \) akkor \ (b \ ekvivalens c = 0 \ ekvivalens = 1, \)\ (F = 1, \), mivel a kötőszóban szereplő mindkét kifejezés igaz (2. sor). Ha \ (c = 1, \) akkor \ (b \ ekvivalens c = 0 \ egyenértékű 1 = 0, \)\ (F = 0, \), mivel a kötőszóban szereplő egyik kifejezés hamis (3. sor).
Így \ (F = 1 \) \ (d = 1 \) esetén (2., 4., 5. sor). A \ (d \) értékek összege 1 * 3 = 3.
Igazságtáblák készítése összetett állításokhoz.
Logikai prioritás
1) inverzió 2) konjunkció 3) diszjunkció 4) implikáció és ekvivalencia
Hogyan készítsünk igazságtáblát?
Definíció szerint a logikai képlet igazságtáblázata a változó értékek különböző halmazai és a képlet értékei közötti megfelelést fejezi ki.
A két változót tartalmazó képlet esetében csak négy ilyen változóérték -készlet létezik:
(0, 0), (0, 1), (1, 0), (1, 1).
Ha egy képlet három változót tartalmaz, akkor nyolc lehetséges értékkészlet létezik (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1) , (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
A négy változót tartalmazó képlet halmazainak száma tizenhat, stb.
A képlet értékeinek megtalálásához kényelmes jelölési forma a táblázat, amely a változók és képletértékek mellett a köztes képletek értékeit is tartalmazza.
Példák.
1. Hozzon létre egy igazságtáblázatot a 96% "style =" width: 96.0% "> képlethez
A táblázat ezt mutatja az x és y változók összes értékkészletére a képlet az 1 értéket veszi fel, vagyis van egyformán igaz.
2. Igazságtáblázat a 96% képlethez "style =" width: 96.0% ">
A táblázat ezt mutatja az x és y változók összes értékkészletére a képletet a 0 értéket veszi fel, vagyis van azonos módon hamis .
3. Igazságtáblázat a 96% képlethez "style =" width: 96.0% ">
A táblázat ezt mutatja képlet 0 "style =" border-collapse: collapse; border: none ">
Következtetés: minden egységet az utolsó oszlopban kaptunk. Ez azt jelenti, hogy egy összetett állítás jelentése igaz az egyszerű K és C állítások bármely értékére. Ezért a tanár logikusan helyesen érvelt.
 A Nem elég elemek kezelése és funkciói mod
A Nem elég elemek kezelése és funkciói mod Hibaelhárítás TLauncher
Hibaelhárítás TLauncher Miért nem az Instagram keresi a helyét: a fő okok?
Miért nem az Instagram keresi a helyét: a fő okok? Hogyan lehet törölni a gyorsítótárat a vk alkalmazásban
Hogyan lehet törölni a gyorsítótárat a vk alkalmazásban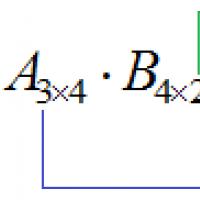 Alapműveletek mátrixokon (összeadás, szorzás, transzponálás) és tulajdonságaik
Alapműveletek mátrixokon (összeadás, szorzás, transzponálás) és tulajdonságaik Lítium -polimer akkumulátorok
Lítium -polimer akkumulátorok A logikai kifejezések azonos konverziói
A logikai kifejezések azonos konverziói