Tablas de verdad de operaciones lógicas cómo resolver. Conversiones idénticas de expresiones lógicas
Hoy hablaremos de una asignatura que se llama informática. Tabla de verdad, tipos de funciones, el orden de su ejecución: estas son nuestras preguntas principales, a las que intentaremos encontrar respuestas en el artículo.
Por lo general, este curso se imparte en la escuela secundaria, pero la gran cantidad de estudiantes es la razón de la falta de comprensión de algunas de las características. Y si va a dedicar su vida a esto, entonces simplemente no puede prescindir de aprobar el examen estatal unificado de informática. Tabla de verdad, transformación de expresiones complejas, resolución de problemas lógicos: todo esto se puede encontrar en el boleto. Ahora analizaremos más de cerca este tema y lo ayudaremos a obtener más puntos en el examen.
El tema de la lógica
¿De qué se trata esta asignatura: informática? Mesa de la verdad: ¿cómo construirla? ¿Por qué se necesita la ciencia de la lógica? Ahora responderemos a todas estas preguntas.
La informática es un tema bastante fascinante. No puede causar dificultades en la sociedad moderna, porque todo lo que nos rodea, de una forma u otra, se refiere a una computadora.
Los profesores de secundaria enseñan los conceptos básicos de la ciencia de la lógica en lecciones de informática. Tablas de verdad, funciones, simplificación de expresiones: todo esto debe ser explicado por el profesor de informática. Esta ciencia es simplemente necesaria en nuestra vida. Míralo más de cerca, todo obedece a unas leyes. Lanzaste la pelota, voló hacia arriba, pero luego cayó al suelo, esto sucedió debido a la presencia de las leyes de la física y la fuerza de la gravedad. Mamá hace sopa y agrega sal. ¿Por qué no obtenemos granos cuando los comemos? Es simple, la sal se disuelve en agua, obedeciendo las leyes de la química.

Ahora preste atención a cómo habla.
- "Si llevo a mi gato a la clínica veterinaria, lo vacunarán".
- "Hoy fue un día muy difícil porque llegó el cheque".
- “No quiero ir a la universidad porque hoy habrá un coloquio”, etcétera.
Todo lo que diga está obligado a obedecer las leyes de la lógica. Esto se aplica tanto a las conversaciones comerciales como a las amistosas. Es por esta razón que es necesario comprender las leyes de la lógica para no actuar al azar, sino para estar seguro del resultado de los eventos.
Funciones
Para compilar una tabla de verdad para el problema que se le propone, necesita conocer las funciones lógicas. ¿Lo que es? Una función lógica tiene algunas variables que son declaraciones (verdaderas o falsas), y el valor de la función en sí debería darnos la respuesta a la pregunta: "¿La expresión es verdadera o falsa?"
Todas las expresiones toman los siguientes valores:
- Verdadero o falso.
- Y o L.
- 1 o 0.
- Más o menos.
Aquí, dé preferencia al método que le resulte más conveniente. Para componer una tabla de verdad, necesitamos enumerar todas las combinaciones de variables. Su número se calcula mediante la fórmula: 2 elevado a n. El resultado del cálculo es el número de combinaciones posibles, la variable n en esta fórmula denota el número de variables en la condición. Si la expresión tiene muchas variables, entonces puedes usar una calculadora o hacer una pequeña tabla para ti mismo elevando dos a una potencia.
En total, se distinguen siete funciones o conexiones en lógica que conectan expresiones:
- Multiplicación (conjunción).
- Suma (disyunción).
- Corolario (implicación).
- Equivalencia.
- Inversión.
- Accidente cerebrovascular de Schaeffer.
- La flecha de Pierce.
La primera operación de la lista se llama "multiplicación lógica". Puede marcarse gráficamente con una marca de verificación invertida, & o *. La segunda operación de nuestra lista es la suma lógica, indicada gráficamente como una marca de verificación, +. Una implicación se llama consecuencia lógica, se indica como una flecha que apunta de una condición a una consecuencia. La equivalencia se indica con una flecha de dos puntas, la función tiene un valor verdadero solo en aquellos casos en que ambos valores toman el valor "1" o "0". La inversión se llama negación lógica. El trazo de Schaeffer se denomina función que niega la conjunción, y la flecha de Peirce se denomina función que niega la disyunción.
Funciones binarias básicas
La tabla de verdad lógica ayuda a encontrar la respuesta al problema, pero para ello es necesario recordar las tablas de funciones binarias. Se proporcionarán en esta sección.

Conjunción (multiplicación). Si hay dos, como resultado obtenemos la verdad, en todos los demás casos obtenemos una mentira.
El resultado es falso con suma lógica, solo tenemos en el caso de dos entradas falsas.
Una consecuencia lógica tiene un resultado falso solo cuando la condición es verdadera y el efecto es falso. Aquí puedes dar un ejemplo de la vida: “Quería comprar azúcar, pero la tienda estaba cerrada”, por lo tanto, nunca se compró azúcar.
La equivalencia es verdadera solo en los casos en que los valores de los datos de entrada son los mismos. Es decir, con pares: "0; 0" o "1; 1".

En el caso de la inversión, todo es elemental, si hay una expresión verdadera en la entrada, se convierte en falsa y viceversa. La imagen muestra cómo se indica gráficamente.
El trazo de Schiffer producirá un resultado falso solo si hay dos expresiones verdaderas.
En el caso de la flecha de Pierce, la función será verdadera solo si solo tenemos expresiones falsas como entrada.
En que orden realizar operaciones lógicas
Tenga en cuenta que la construcción de tablas de verdad y la simplificación de expresiones solo es posible si el orden de las operaciones es correcto. Recuerda en qué secuencia deben realizarse, esto es muy importante para obtener el resultado correcto.
- negación lógica;
- multiplicación;
- adición;
- consecuencia;
- equivalencia;
- negación de la multiplicación (trazo de Schaeffer);
- negación de la adición (flecha de Pierce).
Ejemplo 1
Ahora proponemos considerar un ejemplo de construcción de una tabla de verdad para 4 variables. Es necesario averiguar en qué casos F = 0 para la ecuación: notA + B + C * D
La respuesta a esta tarea será enumerar las siguientes combinaciones: "1; 0; 0; 0", "1; 0; 0; 1" y "1; 0; 1; 0". Como puede ver, hacer una tabla de verdad es bastante simple. Una vez más, me gustaría llamar su atención sobre el orden de ejecución de las acciones. En un caso concreto, fue el siguiente:
- Inversión de la primera expresión simple.
- La conjunción de la tercera y cuarta expresiones.
- Disyunción de la segunda expresión con los resultados de cálculos anteriores.
Ejemplo No. 2

Ahora consideraremos otra tarea que requiere la construcción de una tabla de verdad. La informática (se tomaron ejemplos del curso escolar) también puede tener como tarea. Echemos un vistazo rápido a uno de ellos. ¿Vanya es culpable de robar el balón si se sabe lo siguiente?
- Si Vanya no robó o Petya robó, Seryozha participó en el robo.
- Si Vanya no es culpable, entonces Seryozha tampoco robó el balón.
Introduzcamos las designaciones: I - Vanya robó la pelota; P - Petya robó; S - Seryozha robó.
De acuerdo con esta condición, podemos componer la ecuación: F = ((no И + П) implicación С) * (no e implicación noС). Necesitamos esas opciones en las que la función adquiere un valor real. A continuación, debe crear una tabla, ya que esta función tiene hasta 7 acciones, las omitiremos. Solo ingresaremos los datos de entrada y el resultado.
Tenga en cuenta que en este problema usamos más y menos en lugar de los signos "0" y "1". Esto también es aceptable. Estamos interesados en combinaciones donde F = +. Después de analizarlos, podemos sacar la siguiente conclusión: Vanya participó en el robo de la pelota, ya que en todos los casos donde F toma el valor +, Y tiene un valor positivo.
Ejemplo No. 3

Ahora te sugerimos que encuentres el número de combinaciones cuando F = 1. La ecuación tiene la siguiente forma: F = notA + B * A + notB. Creamos una tabla de verdad:
Respuesta: 4 combinaciones.
Operaciones lógicas básicas
Negación (inversión), del latín inversio - invertir:
Corresponde a la partícula NO, la frase es QUÉ INCORRECTO;
Designación: no A, A, -A;
mesa de la verdad:
La inversa de una variable booleana es verdadera si la variable en sí es falsa y, a la inversa, la inversa es falsa si la variable es verdadera.
Ejemplo: A = (Está nevando afuera).
A = (No es cierto que esté nevando afuera)
A = (No está nevando afuera);
Adición lógica (disyunción), del latín disjunctio - distingo:
Coincide con la unión OR;
Designación: +, o, o, V;
Mesa de la verdad:
La disyunción es falsa si y solo si ambas declaraciones son falsas.
Ejemplo: F = (El sol brilla afuera o sopla un viento fuerte);
Multiplicación lógica (conjunción), del latín conjunctio - conecto:
Coincide con unión Y
(en lenguaje natural: tanto A como B, tanto A como B, A junto con B, A, a pesar de B, A, mientras que B);
Designación: Ч ,, &, y, ^, y;
Mesa de la verdad:
Una conjunción es verdadera si y solo si ambas declaraciones son verdaderas.
Ejemplo: F = (El sol brilla afuera y sopla un viento fuerte);
Cualquier enunciado complejo se puede escribir usando las operaciones lógicas básicas Y, O, NO. Con la ayuda de los circuitos lógicos Y, O, NO es posible implementar una función lógica que describa el funcionamiento de varios dispositivos informáticos.
2) La tabla de verdad es una tabla que describe una función lógica.
En este caso, una "función lógica" significa una función en la que los valores de las variables (parámetros de la función) y el valor de la función en sí expresan verdad lógica. Por ejemplo, en la lógica de dos valores, pueden tomar los valores "verdadero" o "falso" (o bien).
La definición tabular de funciones se encuentra no solo en la lógica, sino que para las funciones lógicas, las tablas resultaron ser especialmente convenientes, y desde principios del siglo XX se les asignó este nombre especial. Las tablas de verdad se utilizan especialmente en el álgebra de Boole y en sistemas lógicos de valores múltiples similares.
Una conjunción es una operación lógica, que en su aplicación es lo más cercana posible a la conjunción "y". Multiplicación lógica, a veces simplemente "Y".
La disyunción es una operación lógica, que en su aplicación se acerca lo más posible a la conjunción "o" en el sentido de "esto, o esto, o ambos a la vez". suma lógica, a veces simplemente "O".
La implicación es una conectiva lógica binaria, en su aplicación cercana a las conjunciones "si ... entonces ..." La implicación se escribe como premisa de una consecuencia; También se utilizan flechas de diferente forma y dirigidas en la otra dirección (el punto siempre indica el efecto).
La equivalencia (o equivalencia) es una operación lógica de dos lugares. Normalmente se indica con el símbolo ≡ o ↔.
7. Expresiones lógicas, tablas de verdad de expresiones lógicas.
Una expresión lógica es un registro o una declaración verbal que, junto con las constantes, necesariamente incluye cantidades variables (objetos). Dependiendo de los valores de estas variables, la expresión lógica puede tomar uno de dos valores posibles: VERDADERO (1 lógico) o FALSO (0 lógico)
Una expresión lógica compleja es una expresión lógica compuesta por una o más expresiones lógicas simples (o complejas) asociadas con operaciones lógicas.
Operaciones lógicas y tablas de verdad
Multiplicación lógica CONJUNCIÓN: esta nueva expresión compleja solo será verdadera si ambas expresiones simples originales son verdaderas. La conjunción define la conexión de dos expresiones lógicas usando la unión de I.
Suma lógica - DISYUNCIÓN - esta nueva expresión compleja será verdadera si y solo si al menos una de las expresiones originales (simples) es verdadera. La disyunción define la conexión de dos expresiones lógicas usando la conjunción OR
Negación lógica: INVERSIÓN - si la expresión original es verdadera, entonces el resultado de la negación será falso, y viceversa, si la expresión original es falsa, el resultado de la negación será verdadero / Esta operación significa que la partícula NO o la palabra INCORRECTO se agrega a la expresión lógica original, QUÉ
Consecuencia lógica: IMPLICACIÓN: conecta dos expresiones lógicas simples, de las cuales la primera es una condición (A) y la segunda (B) es una consecuencia de esta condición. El resultado de la IMPLICACIÓN es FALSO solo si la condición A es verdadera y la consecuencia B es falsa. Se denota con el símbolo "por lo tanto" y se expresa con las palabras SI ..., ENTONCES ...
Equivalencia lógica: EQUIVALENCIA: determina el resultado de comparar dos expresiones lógicas simples A y B. El resultado de EQUIVALENCIA es una nueva expresión lógica que será verdadera si y solo si ambas expresiones originales son simultáneamente verdaderas o falsas. Indicado por el símbolo "equivalencia"
El orden de realizar operaciones lógicas en una expresión lógica compleja:
1.inversión
2. conjunción
3.disyunción
4.implicación
5.equivalencia
Los paréntesis se utilizan para cambiar el orden especificado de operaciones.
Construyendo tablas de verdad para expresiones complejas:
Número de líneas = 2n + dos líneas para el título (n es el número de declaraciones simples)
Número de columnas = número de variables + número de operaciones lógicas
Al construir una tabla, es necesario tener en cuenta todas las combinaciones posibles de los valores lógicos 0 y 1 de las expresiones originales. Luego, determine el orden de las acciones y elabore una tabla, teniendo en cuenta las tablas de verdad de las principales operaciones lógicas.
EJEMPLO: compile una tabla de verdad de una expresión lógica compleja D = notA & (B + C)
A, B, C - tres declaraciones simples, por lo tanto:
número de líneas = 23 +2 = 10 (n = 3, ya que hay tres elementos A, B, C en la entrada)
número de columnas: 1) A
4) no A es el inverso de A (denotado por E)
5) B + C es una operación de disyunción (denote F)
6) D = notA & (B + C), es decir D = E & F es una operación de conjunción
A B C E = no A (no 1) F = B + C (2 + 3) D = E&F (4 * 5)
Álgebra de la lógica
Álgebra de la lógica
Álgebra de la lógica(ing. álgebra de la lógica) - una de las secciones principales de la lógica matemática, en la que los métodos del álgebra se utilizan en transformaciones lógicas.
El fundador del álgebra de la lógica es el matemático y lógico inglés J. Boole (1815-1864), quien basó su enseñanza lógica en la analogía entre álgebra y lógica. Escribió cualquier enunciado utilizando los símbolos del lenguaje que desarrolló y recibió "ecuaciones", cuya veracidad o falsedad podría probarse con base en ciertas leyes lógicas, como las leyes de conmutatividad, distributividad, asociatividad, etc.
Moderno álgebra de la lógica es una rama de la lógica matemática y estudia las operaciones lógicas sobre enunciados desde el punto de vista de su valor de verdad (verdadero, falso). Las declaraciones pueden ser verdaderas, falsas o contener verdadero y falso en diferentes proporciones.
Declaración lógica Es cualquier oración declarativa respecto de la cual se puede afirmar sin ambigüedades que su contenido es verdadero o falso.
Por ejemplo, "3 por 3 es igual a 9", "Arkhangelsk al norte de Vologda" son afirmaciones verdaderas y "Cinco es menos que tres", "Marte es una estrella" son falsas.
Evidentemente, no toda oración puede ser un enunciado lógico, ya que no siempre tiene sentido hablar de su falsedad o verdad. Por ejemplo, la afirmación "La informática es un tema interesante" es vaga y requiere información adicional, y la afirmación "Para un estudiante de grado 10-A, AA Ivanov, la informática es una asignatura interesante", según los intereses de AA Ivanov, puede tomar sobre el significado de "verdad" o "mentira".
excepto álgebra proposicional de dos valores, en el que solo se aceptan dos valores: "verdadero" y "falso", hay álgebra proposicional multivalor. En tal álgebra, además de los significados "verdadero" y "falso", se utilizan valores de verdad como "probablemente", "posible", "imposible", etc.
En álgebra, las lógicas difieren sencillo(elemental) declaraciones, denotado por letras latinas (A, B, C, D, ...), y complejo(compuesto), compuesto por varios simples que utilizan conectivos lógicos, por ejemplo, como "No", "y", "o", "entonces y solo entonces", "si ... entonces"... La veracidad o falsedad de enunciados complejos obtenidos de esta manera está determinada por el significado de enunciados simples.
Denotemos como A el enunciado "El álgebra de la lógica se aplica con éxito en la teoría de circuitos eléctricos", y a través de V- "El álgebra de la lógica se utiliza en la síntesis de circuitos relé-contacto".
Entonces, el enunciado compuesto "El álgebra de la lógica se aplica con éxito en la teoría de circuitos eléctricos y en la síntesis de circuitos de contacto de relé" se puede escribir brevemente como A y B; aquí "y" es un conectivo lógico. Obviamente, dado que las declaraciones elementales A y B son verdaderas, entonces el enunciado compuesto A y B.
Cada conectivo lógico se considera una operación sobre enunciados lógicos y tiene su propio nombre y designación.
Solo hay dos valores lógicos: verdad verdad) y falso (FALSO)... Esto corresponde a la representación digital - 1 y 0 ... Los resultados de cada operación lógica se pueden registrar en forma de tabla. Estas tablas se denominan tablas de verdad.
Operaciones básicas del álgebra de Boole
1. Negación lógica, inversión(lat. inversión- inversión) es una operación lógica, como resultado de la cual se obtiene una nueva declaración a partir de una declaración dada (por ejemplo, A) ( No un), Lo que es llamado negación de la declaración original, denotado simbólicamente por una barra arriba ($ A↖ (-) $) o por convenciones tales como ¬, "no" y lee: "No A", "A es falso", "no es cierto que A", "negación de A"... Por ejemplo, "Marte es un planeta del sistema solar" (diciendo A); “Marte no es un planeta del sistema solar” ($ A↖ (-) $); el enunciado "10 es un número primo" (enunciado B) es falso; el enunciado “10 no es un número primo” (enunciado B) es verdadero.
Una operación utilizada con respecto a una cantidad se llama unario... La tabla de valores de esta operación tiene la forma
El enunciado $ A↖ (-) $ es falso cuando A es verdadero y verdadero cuando A es falso.
Geométricamente, la negación se puede representar de la siguiente manera: si A es un conjunto de puntos, entonces $ A↖ (-) $ es el complemento del conjunto A, es decir, todos los puntos que no pertenecen al conjunto A.
2.Conjunción(lat. conjuntio- conexión) - multiplicación lógica, una operación que requiere al menos dos valores lógicos (operandos) y conecta dos o más declaraciones usando un enlace "y"(por ejemplo, "A y B"), que se denota simbólicamente con el signo ∧ (A ∧ B) y dice: "A y B". Los siguientes signos también se utilizan para indicar conjunción: A ∙ B; A y B, A y B y, a veces, no se pone ningún signo entre las declaraciones: AB. Un ejemplo de multiplicación lógica: "Este triángulo es isósceles y de ángulo recto". Un enunciado dado solo puede ser verdadero si se cumplen ambas condiciones; de lo contrario, el enunciado es falso.
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Declaración A ∧ V es cierto solo si ambas declaraciones - A y V son verdaderas.
Geométricamente, una conjunción se puede representar de la siguiente manera: si A, B A ∧ V hay una intersección de conjuntos A y V.

3. Disyunción(lat. disyunción- separación) - suma lógica, una operación que conecta dos o más declaraciones usando un paquete "o"(por ejemplo, "A o B"), que se denota simbólicamente con el signo ∨ (A∨ V) y lee: "A o B"... Los siguientes signos también se utilizan para indicar disyunción: A + B; A o B; A | B... Un ejemplo de suma lógica: "El número x es divisible entre 3 o 5". Esta afirmación será verdadera si se cumplen ambas condiciones, o al menos una de las condiciones.
La tabla de verdad de la operación tiene la forma
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Declaración A∨ V falso solo si ambas declaraciones - A y V son falsas.
La suma geométricamente lógica se puede representar de la siguiente manera: si A, B Son algunos conjuntos de puntos, entonces A ∨ V Es la unión de conjuntos A y V, es decir, la figura que une tanto el cuadrado como el círculo.

4. Disyunción de separación estricta, módulo de adición dos- una operación lógica que conecta dos declaraciones mediante un enlace "o", usado en el sentido exclusivo, que se denota simbólicamente por los signos ∨ ∨ o ⊕ ( A ∨ ∨ B, A ⊕ V) y lee: "Cualquiera a o B"... Un ejemplo de suma módulo dos es el dicho "Este triángulo es obtuso o agudo". La afirmación es verdadera si alguna de las condiciones es verdadera.
La tabla de verdad de la operación tiene la forma
| A | V | A⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
El enunciado A ⊕ B es verdadero solo cuando los enunciados A y B tienen significados diferentes.
5. Implicación(lat. implisito- estrechamente relacionado) - una operación lógica que conecta dos declaraciones usando un paquete "Si ... entonces" en una declaración compleja, que se denota simbólicamente por el signo → ( A → V) y lee: "Si A, entonces B", "A implica B", "B se sigue de A", "A implica B"... El signo ⊃ (A ⊃ B) también se usa para denotar implicación. Un ejemplo de una implicación: "Si el cuadrilátero resultante es un cuadrado, entonces se puede describir un círculo a su alrededor". Esta operación conecta dos expresiones booleanas simples, de las cuales la primera es una condición y la segunda es una consecuencia. El resultado de una operación es falso solo cuando la premisa es verdadera y el efecto es falso. Por ejemplo, “Si 3 * 3 = 9 (A), entonces el Sol es un planeta (B)”, el resultado de la implicación A → B es falso.
La tabla de verdad de la operación tiene la forma
| A | V | A→V |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Para el funcionamiento de la implicación, es cierto que cualquier cosa puede seguirse de una mentira, y sólo la verdad puede seguirse de la verdad.
6. Equivalencia, doble implicación, equivalencia(lat. aequalis- igual y Valentis- válido) - una operación lógica que permite dos declaraciones A y V obtener una nueva declaración A ≡ B que dice: "A es equivalente a B"... Los siguientes símbolos también se utilizan para denotar equivalencia: ⇔, ∼. Esta operación puede expresarse mediante ligamentos. "Entonces y solo entonces", "necesario y suficiente", "equivalente"... Un ejemplo de equivalencia es la afirmación: "Un triángulo será rectangular si y solo si uno de los ángulos tiene 90 grados".
La tabla de verdad de la operación de equivalencia tiene la forma
| A | V | A∼ V |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
La operación de equivalencia es opuesta a la suma módulo dos y tiene el resultado "verdadero" si y sólo si los valores de las variables coinciden.
Conociendo los significados de enunciados simples, es posible determinar los significados de enunciados complejos sobre la base de tablas de verdad. Es importante saber que tres operaciones son suficientes para representar cualquier función del álgebra de la lógica: conjunción, disyunción y negación.
La prioridad de realizar operaciones lógicas es la siguiente: negación ( "no") tiene la prioridad más alta, luego la conjunción ( "y"), después de conjunción - disyunción ( "o").
Con la ayuda de variables lógicas y operaciones lógicas, cualquier enunciado lógico puede formalizarse, es decir, reemplazarse por una fórmula lógica. Al mismo tiempo, los enunciados elementales que forman un enunciado compuesto pueden no tener ningún significado relacionado, pero esto no interfiere con la determinación de la verdad o falsedad de un enunciado compuesto. Por ejemplo, la declaración "Si cinco es más que dos ( A), el martes siempre viene después del lunes ( V) "- implicación A→ V, y el resultado de la operación en este caso es "verdadero". En las operaciones lógicas no se tiene en cuenta el significado de los enunciados, solo se considera su verdad o falsedad.
Considere, por ejemplo, la construcción de un enunciado compuesto a partir de enunciados A y V lo cual sería falso si y solo si ambas declaraciones son verdaderas. En la tabla de verdad para la operación de suma módulo dos, encontramos: 1 ⊕ 1 = 0. Y el enunciado puede ser, por ejemplo, esto: "Esta bola es completamente roja o completamente azul". Por lo tanto, si la declaración A"Esta bola es completamente roja" es cierto, y la afirmación V"Esta bola es completamente azul" es cierto, entonces la afirmación compuesta es una mentira, porque la bola no puede ser roja y azul al mismo tiempo.
Ejemplos de resolución de problemas
Ejemplo 1. Determine para los valores indicados de X el valor del enunciado lógico ((X> 3) ∨ (X< 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Solución. La secuencia de operaciones es la siguiente: primero se realizan las operaciones de comparación entre paréntesis, luego la disyunción y la última es la operación de implicación. La operación de disyunción ∨ es falsa si y solo si ambos operandos son falsos. La tabla de verdad para la implicación es
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
De aquí obtenemos:
1) para X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) para X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) para X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Ejemplo 2. Especifique el conjunto de valores enteros X para los que la expresión ¬ ((X> 2) → (X> 5)) es verdadera.
Solución. La operación de negación se aplica a toda la expresión ((X> 2) → (X> 5)), por lo tanto, cuando la expresión ¬ ((X> 2) → (X> 5)) es verdadera, la expresión ((X > 2) → (X> 5)) es falso. Por lo tanto, es necesario determinar para qué valores de X la expresión ((X> 2) → (X> 5)) es falsa. La operación de implicación toma el valor "falso" sólo en un caso: cuando de la verdad se sigue falso. Y esto se hace solo para X = 3; X = 4; X = 5.
Ejemplo 3.¿Para cuál de las palabras dadas es falsa la declaración ¬ (primera letra de una vocal ∧ tercera letra de una vocal) ⇔ una cadena de 4 caracteres? 1) asalto; 2) kuku; 3) maíz; 4) error; 5) hombre fuerte.
Solución. Consideremos todas las palabras sugeridas en secuencia:
1) para la palabra culo obtenemos: ¬ (1 ∧ 0) ⇔ 1, 1 ⇔ 1 - el enunciado es verdadero;
2) para la palabra kuku obtenemos: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 - la afirmación es verdadera;
3) para la palabra maíz obtenemos: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 - la afirmación es falsa;
4) para la palabra error obtenemos: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 - la afirmación es verdadera;
5) para la palabra hombre fuerte obtenemos: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 - la afirmación es falsa.
Expresiones booleanas y su transformación
Debajo expresión lógica debe comprender un registro de este tipo que puede tomar el valor lógico "verdadero" o "falso". Con esta definición, es necesario distinguir entre expresiones lógicas:
- expresiones que utilizan operaciones de comparación ("mayor que", "menor que", "igual", "no igual", etc.) y toman valores lógicos (por ejemplo, la expresión a> b, donde a = 5 y b = 7, es igual al valor "falso");
- Expresiones lógicas directas asociadas con valores lógicos y operaciones lógicas (por ejemplo, A ∨ B ∧ C, donde A = verdadero, B = falso y C = verdadero).
Las expresiones booleanas pueden incluir funciones, operaciones algebraicas, operaciones de comparación y operaciones lógicas. En este caso, la prioridad para realizar acciones es la siguiente:
- cálculo de dependencias funcionales existentes;
- realizar operaciones algebraicas (primero multiplicación y división, luego resta y suma);
- realizar operaciones de comparación (sin ningún orden en particular);
- ejecución de operaciones lógicas (al inicio se realizan operaciones de negación, luego operaciones de multiplicación lógica, suma lógica, las últimas operaciones de implicación y equivalencia).
Las expresiones booleanas pueden usar paréntesis que cambian el orden en que se realizan las operaciones.
Ejemplo. Encuentra el valor de una expresión:
$ 1 ≤ a ∨ A ∨ sin (π / a - π / b)< 1 ∧ ¬B ∧ ¬(b^a + a^b >a + b ∨ A ∧ B) $ para a = 2, b = 3, A = verdadero, B = falso.
Solución. El orden de contar los valores:
1) b a + a b> a + b, después de la sustitución obtenemos: 3 2 + 2 3> 2 + 3, es decir, 17> 2 + 3 = verdadero;
2) A ∧ B = verdadero ∧ falso = falso.
Por lo tanto, la expresión entre paréntesis es (b a + a b> a + b ∨ A ∧ B) = verdadero ∨ falso = verdadero;
3) 1≤ a = 1 ≤ 2 = verdadero;
4) pecado (π / a - π / b)< 1 = sin(π/2 - π/3) < 1 = истина.
Después de estos cálculos, finalmente obtenemos: verdad ∨ А ∧ verdadero ∧ ¬В ∧ ¬ verdadero.
Ahora se deben realizar las operaciones de negación, seguidas de la multiplicación lógica y la suma:
5) ¬В = ¬false = verdadero; ¬verdadero = falso;
6) A ∧ verdadero ∧ verdadero ∧ falso = verdadero ∧ verdadero ∧ verdadero ∧ falso = falso;
7) verdadero ∨ falso = verdadero.
Por lo tanto, el resultado de una expresión booleana con valores dados es "verdadero".
Nota. Considerando que la expresión original es, al final, la suma de dos términos, y el valor de uno de ellos es 1 ≤ a = 1 ≤ 2 = verdadero, sin más cálculos podemos decir que el resultado para toda la expresión también es "cierto".
Conversiones idénticas de expresiones lógicas
En el álgebra de la lógica se cumplen las leyes básicas que permiten realizar transformaciones idénticas de expresiones lógicas.
| Ley | Para ∨ | Para ∧ |
| Propulsor | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Combinativo | UNA ∨ (B ∨ C) = (B ∨ A) ∨ C | UNA ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Unión | UNA ∧ (B ∨ C) = (UNA ∧ B) ∨ (A ∧ C) | UNA ∨ B ∧ C = (UNA ∨ B) ∧ (UNA ∨ C) |
| Las reglas de De Morgan | $ (A ∨ B) ↖ (-) $ = $ A↖ (-) ∧ B↖ (-) $ | $ (A ∧ B) ↖ (-) $ = $ A↖ (-) ∨ B↖ (-) $ |
| Idempotencias | A ∨ A = A | A ∧ A = A |
| Absorción | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Encolado | (A ∧ B) ∨ (A↖ (-) ∧ B) = B | (A ∨ B) ∧ (A↖ (-) ∨ B) = B |
| Operación variable con su inversión | $ A ∨ A↖ (-) $ = 1 | $ A ∧ A↖ (-) $ = 0 |
| Operación con constantes | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Doble negación | $ A↖ (=) $ = A | |
Las pruebas de estas afirmaciones se realizan sobre la base de la construcción de tablas de verdad para los registros correspondientes.
Las transformaciones equivalentes de fórmulas lógicas tienen el mismo propósito que las transformaciones de fórmulas en álgebra ordinaria. Sirven para simplificar fórmulas o llevarlas a una determinada forma utilizando las leyes básicas del álgebra de la lógica. Debajo simplificación de la fórmula, que no contiene las operaciones de implicación y equivalencia, se entiende como una transformación equivalente que conduce a una fórmula que contiene menos operaciones que el número original o menos variables.
Algunas transformaciones de fórmulas lógicas son similares a las transformaciones de fórmulas en álgebra ordinaria (tomando el factor común fuera del paréntesis, usando las leyes de desplazamiento y combinación, etc.), mientras que otras transformaciones se basan en propiedades que las operaciones del álgebra ordinaria no tienen. (usando la ley de distribución para conjunción, leyes de absorción, encolado, de Morgan, etc.).
Veamos ejemplos de algunas de las técnicas y métodos utilizados para simplificar fórmulas lógicas:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2.
Para la transformación aquí puede aplicar la ley de la idempotencia, la ley de distribución; una operación de variable inversa y una operación constante.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1.
Aquí, por simplicidad, se aplica la ley de absorción.
3) ¬ (X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1.
Al transformar, regla de Morgan, se aplica la operación de una variable con su inversión, una operación con una constante
Ejemplos de resolución de problemas
Ejemplo 1. Encuentre una expresión booleana equivalente a A ∧ ¬ (¬B ∨ C).
Solución. Aplicamos la regla de De Morgan para B y C: ¬ (¬B ∨ C) = B ∧ ¬C.
Obtenemos una expresión equivalente a la original: A ∧ ¬ (¬B ∨ C) = A ∧ B ∧ ¬C.
Respuesta: A ∧ B ∧ ¬C.
Ejemplo 2. Indique el valor de las variables lógicas A, B, C, para las cuales el valor de la expresión lógica (A ∨ B) → (B ∨ ¬C ∨ B) es falso.
Solución. La operación de implicación es falsa solo en el caso en que una falsedad se sigue de la premisa verdadera. Por tanto, para una expresión dada, la premisa A ∨ B debe tomar el valor "verdadero", y la consecuencia, es decir, la expresión B ∨ ¬C ∨ B, debe tomar el valor "falso".
1) A ∨ B - el resultado de la disyunción es "verdadero" si al menos uno de los operandos es "verdadero";
2) B ∨ ¬C ∨ B - la expresión es falsa si todos los términos tienen el valor "falso", es decir, B - "falso"; ¬C - "falso", y por lo tanto, la variable C tiene el valor "verdadero";
3) si consideramos la premisa y tenemos en cuenta que B es “falso”, obtenemos que el valor de A es “verdadero”.
Respuesta: A es verdadero, B es falso, C es verdad.
Ejemplo 3.¿Cuál es el entero más grande X para el cual la declaración (35
Solución. Escribamos la tabla de verdad para la operación de implicación:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Expresión X< (X - 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Respuesta: X = 5.
Uso de expresiones booleanas para describir regiones geométricas
Las expresiones booleanas se pueden utilizar para describir áreas geométricas. En este caso, el problema se formula de la siguiente manera: para una región geométrica dada, escriba una expresión lógica que tome el valor "verdadero" para los valores x, y si y solo si cualquier punto con coordenadas (x; y ) pertenece a la región geométrica.
Consideremos la descripción de un área geométrica usando una expresión lógica usando ejemplos.
Ejemplo 1. Se especifica una imagen de un área geométrica. Escribe una expresión booleana que describa el conjunto de puntos que le pertenecen.
1)  .
.
Solución. Una región geométrica dada se puede representar como un conjunto de las siguientes regiones: la primera región - D1 - semiplano $ (x) / (- 1) + (y) / (1) ≤ 1 $, la segunda - D2 - círculo con centro en el origen $ x ^ 2 + y ^ 2 ≤ 1 $. Su intersección D1 $ ∩ $ D2 es el dominio deseado.

Resultado: expresión booleana $ (x) / (- 1) + (y) / (1) ≤ 1 ∧ x ^ 2 + y ^ 2 ≤ 1 $.
2) 
Esta área se puede escribir así: | x | ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1.
Nota. Al construir una expresión lógica, se utilizan desigualdades débiles, lo que significa que los límites de las figuras también pertenecen al área sombreada. Si se utilizan desigualdades estrictas, no se tendrán en cuenta los límites. Los bordes que no pertenecen a la región generalmente se muestran con una línea de puntos.
Puede resolver el problema inverso, a saber: dibujar un área para una expresión lógica dada.
Ejemplo 2. Dibujar y sombrear un área para cuyos puntos se satisfaga la condición lógica y ≥ x ∧ y + x ≥ 0 ∧ y< 2 .
Solución. El área buscada es la intersección de tres semiplanos. Construimos sobre el plano (x, y) líneas rectas y = x; y = -x; y = 2. Estos son los límites del área, y el último límite y = 2 no pertenece al área, por lo que lo dibujamos con una línea de puntos. Para cumplir con la desigualdad y ≥ x, es necesario que los puntos estén a la izquierda de la línea y = x, y la desigualdad y = -x se satisfaga para los puntos que están a la derecha de la línea y = -x. Condición y< 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:

Usar funciones lógicas para describir circuitos eléctricos
Las funciones lógicas son muy útiles para describir el funcionamiento de circuitos eléctricos. Entonces, para el circuito que se muestra en la Fig., Donde el valor de la variable X es el estado del interruptor (si está encendido, el valor de X es "verdadero", y si está apagado, es "falso") , este valor de Y es el estado de la bombilla (si está encendida, el valor es "verdadero", y si no es así, "falso"), la función lógica se escribirá de la siguiente manera: Y = X. La función Y se llama función de la conductividad.

Para el circuito que se muestra en la Fig., La función lógica Y tiene la forma: Y = X1 ∪ X2, ya que un interruptor encendido es suficiente para que la luz se queme. En el diagrama de la Fig., Para que la luz se queme, ambos interruptores deben estar encendidos, por lo tanto, la función de conductividad tiene la forma: Y = X1 ∧ X2.

Para un circuito más complejo, la función de conductancia será: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).

El circuito también puede contener contactos de cierre. En este caso, el contacto abierto como interruptor asegura que la luz se encienda cuando se suelta el botón y no se presiona. Para tales circuitos, el interruptor de desconexión se describe mediante negación.
Los dos esquemas se llaman equivalente a si la corriente pasa por uno de ellos cuando también pasa por el otro. De los dos circuitos equivalentes, el más simple es el circuito, cuya función de conductividad contiene menos elementos. La tarea de encontrar los esquemas más simples entre los equivalentes es muy importante.
Usando el aparato de álgebra lógica en el diseño de circuitos lógicos
El álgebra de las matemáticas lógicas es muy útil para describir cómo funciona el hardware de la computadora. Cuando se procesa en una computadora, cualquier información se representa en forma binaria, es decir, se codifica mediante alguna secuencia de 0 y 1. El procesamiento de las señales binarias correspondientes a 0 y 1 se realiza en la computadora mediante elementos lógicos. Puertas lógicas que realizan operaciones lógicas básicas Y, O, NO, se muestran en la Fig.

Los símbolos de los elementos lógicos son estándar y se utilizan al componer circuitos lógicos de una computadora. Con estos circuitos, puede implementar cualquier función lógica que describa el funcionamiento de una computadora.
Técnicamente, un elemento lógico informático se implementa en forma de circuito eléctrico, que es una conexión de varias partes: diodos, transistores, resistencias, condensadores. La entrada de un elemento lógico, que también se llama puerta, recibe señales eléctricas de niveles de voltaje alto y bajo, y también se da una señal de salida, ya sea alta o baja, en la salida. Estos niveles corresponden a uno de los estados del sistema binario: 1 - 0; VERDADERO es FALSO. Cada elemento lógico tiene su propio símbolo, que expresa su función lógica, pero no indica qué tipo de circuito electrónico se implementa en él. Esto facilita la escritura y la comprensión de circuitos lógicos complejos. El funcionamiento de los circuitos lógicos se describe mediante tablas de verdad. Notación convencional en el circuito OR, el signo "1" - de la notación de disyunción obsoleta como "> = 1" (el valor de la disyunción es 1 si la suma de los dos operandos es mayor o igual a 1). El signo "&" en el diagrama Y es una abreviatura de la palabra inglesa y.
Los circuitos lógicos electrónicos están compuestos por elementos lógicos que realizan operaciones lógicas más complejas. Un conjunto de elementos lógicos que consta de elementos NOT, OR y AND, con los que se puede construir una estructura lógica de cualquier complejidad, se denomina funcionalmente completo.
Creación de tablas de verdad de expresiones booleanas
Para una fórmula lógica, siempre puedes escribir mesa de la verdad, es decir, representar una función lógica dada en forma tabular. En este caso, la tabla debe contener todas las combinaciones posibles de argumentos de función (fórmulas) y los valores de función correspondientes (resultados de la fórmula en un conjunto de valores dado).
Una forma conveniente de notación para encontrar los valores de una función es una tabla que contiene, además de los valores de las variables y los valores de las funciones, también los valores de los cálculos intermedios. Considere un ejemplo de construcción de una tabla de verdad para la fórmula $ (X1) ↖ (-) ∧ X2 ∨ (X1 ∨ X2) ↖ (-) ∨ X1 $.
| X1 | X2 | $ (X1) ↖ (-) $ | $ (X1) ↖ (-) $ \ X2 | X1 ∧ X2 | $ (X1 ∨ X2) ↖ (-) $ | $ (X1) ↖ (-) $ ∧ X2 ∨ $ (X1 ∨ X2) ↖ (-) $ | $ (X1) ↖ (-) $ ∧ X2 ∨ $ (X1 ∨ X2) ↖ (-) $ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Si una función toma el valor 1 para todos los conjuntos de valores de variables, es idénticamente cierto; si para todos los conjuntos de valores de entrada la función toma el valor 0, es idénticamente falso; si el conjunto de valores de salida contiene 0 y 1, la función se llama factible... El ejemplo anterior es un ejemplo de una función idénticamente verdadera.
Conociendo la forma analítica de una función lógica, siempre se puede pasar a la forma tabular de funciones lógicas. Con la ayuda de una tabla de verdad dada, es posible resolver el problema inverso, a saber: para una tabla dada, construir una fórmula analítica para una función lógica. Hay dos formas de construir la dependencia analítica de una función lógica de acuerdo con una función de tabla dada.
1. Forma normal disyuntiva (DNF)- la suma de productos formados a partir de variables y sus negaciones para valores falsos.
El algoritmo para construir DNF es el siguiente:
- en la tabla de verdad de la función, se seleccionan conjuntos de argumentos cuyas formas lógicas son iguales a 1 ("verdadero");
- todos los conjuntos lógicos seleccionados se escriben como productos lógicos de argumentos, conectándolos secuencialmente entre sí mediante la operación de una suma lógica (disyunción);
- para argumentos que son falsos, la operación de negación se aplica al registro construido.
Ejemplo. Construya una función que determine que el primer número es igual al segundo usando el método DNF. La tabla de verdad de la función tiene la forma
| X1 | X2 | F (X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Solución. Seleccionamos los conjuntos de valores de argumentos en los que la función es igual a 1. Estas son la primera y cuarta filas de la tabla (la fila del título no se tiene en cuenta al realizar la numeración).
Escribimos los productos lógicos de los argumentos de estos conjuntos, combinándolos con una suma lógica: X1 ∧ X2 ∨ X1 ∧ X2.
Escribimos la negación con respecto a los argumentos de los conjuntos seleccionados que tienen un valor falso (la cuarta fila de la tabla; el segundo conjunto en la fórmula; el primer y segundo elementos): X1 ∧ X2 ∨ $ (X1) ↖ ( -) $ ∧ $ (X2) ↖ (-) $.
Respuesta: F (X1, X2) = X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ $ (X2) ↖ (-) $.
2. Forma conjuntiva normal (CNF)- el producto de las sumas formadas a partir de las variables y sus negaciones por los valores verdaderos.
El algoritmo para construir el CNF es el siguiente:
- en la tabla de verdad, se seleccionan conjuntos de argumentos cuyas formas lógicas son iguales a 0 ("falso");
- todos los conjuntos lógicos seleccionados como sumas lógicas de argumentos se escriben secuencialmente, conectándolos mediante la operación de un producto lógico (conjunción);
- para los argumentos que son verdaderos, la operación de negación se coloca en el registro construido.
Ejemplos de resolución de problemas
Ejemplo 1. Considere el ejemplo anterior, es decir, construya una función que determine que el primer número es igual al segundo, usando el método CNF. Para una función dada, su tabla de verdad tiene la forma
| X1 | X2 | F (X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Solución. Seleccionamos conjuntos de valores de argumentos en los que la función es igual a 0. Estas son la segunda y tercera línea (la línea de título no se tiene en cuenta al numerar).
Escribimos las sumas lógicas de los argumentos de estos conjuntos, combinándolos con un producto lógico: X1 ∨ X2 ∧ X1 ∨ X2.
Escribimos la negación con respecto a los argumentos de los conjuntos seleccionados que tienen un valor verdadero (la segunda fila de la tabla, el primer conjunto de la fórmula, el segundo elemento; para la tercera fila, este es el segundo conjunto de la fórmula , el primer elemento): X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2.
Así, se ha obtenido un registro de la función lógica en el CNF.
Respuesta: X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2.
Los valores de la función obtenidos por los dos métodos son equivalentes. Para probar esta afirmación, usamos las reglas de la lógica: F (X1, X2) = X1 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ X2 = X1 ∧ $ (X1) ↖ (-) $ ∨ X1 ∧ X2 ∨ $ (X2) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ $ (X2) ↖ (-) $ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $ (X2) ) ↖ (-) $ ∧ $ (X1) ↖ (-) $ ∨ 0 = X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ $ (X2) ↖ (-) $.
Ejemplo 2... Construya una función booleana para una tabla de verdad dada:
La fórmula buscada: X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ X2.
Se puede simplificar: X1 ∧ X2 ∨ $ (X1) ↖ (-) $ ∧ X2 = X2 ∧ (X1 ∨ $ (X1) ↖ (-) $) = X2 ∧ 1 = X2.
Ejemplo 3. Para la tabla de verdad dada, construya una función lógica usando el método DNF.
| X1 | X2 | X3 | F (X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | X1 ∧ X2 ∧ X3 | |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | $ (X1) ↖ (-) $ ∧ X2 ∧ X3 | |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | X1 ∧ X2 ∧ $ (X3) ↖ (-) $ | |
| 1 | 0 | 0 | 1 | X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $ | |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
La fórmula buscada: X1 ∧ X2 ∧ X ∨ $ (X1) ↖ (-) $ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $ (X3) ↖ (-) $ ∪ X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $.
La fórmula es bastante engorrosa y debería simplificarse:
X1 ∧ X2 ∧ X3 ∨ $ (X1) ↖ (-) $ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $ (X3) ↖ (-) $ ∨ X1 ∧ $ (X2) ↖ (-) $ ∧ $ (X3) ↖ (-) $ = X2 ∧ X3 ∧ (X1 ∨ $ (X1) ↖ (-) $) ∨ X1 ∧ $ (X3) ↖ (-) $ ∧ (X2 ∨ $ (X2) ↖ (-) $) = X2 ∧ X3 ∨ X1 ∧ $ (X3) ↖ (-) $.
Tablas de verdad para resolver problemas de lógica
La compilación de tablas de verdad es una de las formas de resolver problemas lógicos. Al utilizar esta solución, las condiciones que contiene el problema se corrigen mediante tablas compiladas especialmente.
Ejemplos de resolución de problemas
Ejemplo 1. Cree una tabla de verdad para un dispositivo de seguridad que usa tres sensores y se activa cuando solo dos de ellos están cerrados.
Solución. Obviamente, la solución dará como resultado una tabla en la que la función deseada Y (X1, X2, X3) tendrá el valor "verdadero" si dos variables cualquiera tienen el valor "verdadero".
| X1 | X2 | X3 | Y (X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Ejemplo 2. Haga un horario de lecciones para el día, teniendo en cuenta que una lección de informática solo puede ser la primera o la segunda, una lección de matemáticas, la primera o la tercera, y la física, la segunda o la tercera. ¿Es posible crear un horario que cumpla con todos los requisitos? ¿Cuántas opciones de programación hay?
Solución. El problema se resuelve fácilmente si elabora la tabla adecuada:
| 1ra lección | 2da lección | 3ra lección | |
| Ciencias de la Computación | 1 | 1 | 0 |
| Matemáticas | 1 | 0 | 1 |
| Física | 0 | 1 | 1 |
La tabla muestra que hay dos opciones para el horario deseado:
- matemáticas, informática, física;
- informática, física, matemáticas.
Ejemplo 3. Tres amigos vinieron al campamento deportivo: Peter, Boris y Alexey. A cada uno le gustan dos deportes. Se sabe que hay seis deportes de este tipo: fútbol, hockey, esquí, natación, tenis, bádminton. También se sabe que:
- Boris es el mayor;
- el que juega al fútbol es más joven que el que juega al hockey;
- jugando al fútbol y al hockey y Peter vive en la misma casa;
- cuando surge una pelea entre un esquiador y un tenista, Boris los reconcilia;
- Peter no puede jugar al tenis ni al bádminton.
¿Qué tipo de deportes disfruta cada uno de los niños?
Solución. Compongamos una tabla y reflejemos en ella las condiciones del problema, llenando las celdas correspondientes con los números 0 y 1, dependiendo de si el enunciado correspondiente es falso o verdadero.
Dado que hay seis tipos de deportes, resulta que a todos los niños les gustan los diferentes deportes.
De la condición 4 se deduce que a Boris no le gusta el esquí o el tenis, pero de las condiciones 3 y 5 que Peter no sabe jugar fútbol, hockey, tenis y bádminton. Por lo tanto, los deportes favoritos de Peter son el esquí y la natación. Ingresemos esto en la tabla y llenemos las celdas restantes de las columnas "Esquí" y "Natación" con ceros.
La tabla muestra que solo Alexei puede jugar al tenis.
De las condiciones 1 y 2 se deduce que Boris no es un jugador de fútbol. Así, Alexey juega al fútbol. Sigamos llenando la tabla. Ingresemos ceros en las celdas vacías de la línea "Alexey".
Finalmente, entendemos que a Boris le gusta el hockey y el bádminton. La mesa final se verá así:
Respuesta: A Peter le gusta esquiar y nadar, Boris juega hockey y bádminton, y Alexey juega fútbol y tenis.
Tarea 1 # 10050
\ ((x \ wedge y) \ vee (x \ wedge \ overline y) \ vee (y \ wedge z) \ vee (z \ wedge x) \)
Haz su tabla de la verdad. Para su respuesta, ingrese el número de conjuntos \ ((x, \) \ (y, \) \ (z), \) para los cuales la función es 1.
1. Simplificar \ ((x \ wedge y) \ vee (x \ wedge \ overline y). \)
Por la ley de distribución \ ((y \ cuña x) \ vee (x \ cuña \ overline y) \) = \ (x \ wedge (y \ vee \ overline y). \)\ (y \ vee \ overline y = 1 \) (si \ (y = 0, \) entonces \ (\ overline y \ vee y = 1 \ vee 0 = 1, \) si \ (y = 1, \) entonces \ (\ overline y \ vee y = 0 \ vee 1 = 1). \) Luego \ (x \ cuña (y \ vee \ overline y) = x \ cuña 1 = x. \)
2. Simplificar \ ((y \ cuña z) \ vee (z \ cuña x). \) Por la ley de distribución \ ((y \ cuña z) \ vee (z \ cuña x) = z \ cuña (y \ vee x). \)
3. Obtenemos: \ ((x \ cuña y) \ vee (x \ cuña \ sobrelínea y) \ vee (y \ cuña z) \ vee (z \ cuña x) = x \ vee z \ cuña (y \ vee x). \)
4. La tabla de verdad contiene 8 líneas (las líneas son siempre \ (2 ^ n, \) donde \ (n \) es el número de variables). En nuestro caso, existen 3 variables.
5. Complete la tabla de verdad.
\ [\ begin (matriz) (| c | c | c | c | c | c | c |) \ hline x & y & z & y \ vee x & z \ wedge (y \ vee x) & F = x \ vee z \ wedge (y \ vee x) \\ \ hline 0 & 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 & 0 & 0 \\ \ hline 0 & 1 & 0 & 1 & 0 & 0 \\ \ hline 0 & 1 & 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 1 & 0 & 1 \\ \ hline 1 & 0 & 1 & 1 & 1 & 1 \\ \ hline 1 & 1 & 0 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 1 & 1 & 1 \\ \ hline \ end (matriz) \]
Desde la disyunción \ (x \ vee z \ cuña (y \ vee x) \) es verdadero si al menos uno de los enunciados incluidos en él es verdadero, entonces para \ (x = 1 \) \ (F = 1 \) para cualquier \ (y \) y \ (z \) (líneas 5-8 en la tabla de verdad).
Considere el caso cuando \ (x = 0. \) Entonces el valor de la función dependerá del valor \ (z \ wedge (y \ vee x). \) If \ (z \ wedge (y \ vee x) \ ) es verdadero, entonces y \ (F \) es verdadero, si es falso, entonces \ (F \) es falso. Considere el caso cuando \ (F = 1. \) La conjunción \ ((z \ wedge (y \ vee x)) \) es verdadera si todas las afirmaciones incluidas en ella son verdaderas, es decir, \ (y \ vee x = 1 \) y \ (z = 1. \) \ (x = 0, \) significa \ (y \ vee x = 1, \) cuando \ (y = 1 \) (línea 4).
Si una de las afirmaciones incluidas en la conjunción es falsa, entonces toda la conjunción es falsa. Si \ (x = 0 \) y \ (y = 0, \) entonces \ (y \ vee x = 0. \) Entonces \ (z \ wedge (x \ vee y) = 0 \) para cualquier \ (z \) (líneas 1-2). Dado que \ (x = 0, \) y la segunda declaración en la disyunción \ ((z \ wedge (x \ vee y)), \) también es falsa, entonces toda la función es falsa. Si \ (x = 0 \) y \ (y = 1, \) entonces \ (y \ vee x = 1. \) Si \ (z = 0, \) \ (z \ wedge (y \ vee x) = 0. \) Entonces \ (F = 0 \) (línea 3). El caso en el que \ (z = 1, \) \ (y = 1, \) \ (x = 0, \) se consideró en el párrafo anterior.
Hemos construido una tabla de la verdad. Vemos que hay 5 conjuntos en él, para los cuales \ (F = 1. \) Por lo tanto, la respuesta es 5.
Respuesta: 5
Misión 2 # 10051
La función lógica \ (F \) viene dada por la expresión:
\ ((x \ wedge \ overline y \ wedge z) \ vee (x \ rightarrow y) \)
Haz su tabla de la verdad. Para su respuesta, ingrese el número de conjuntos \ ((x, \) \ (y, \) \ (z), \) para los cuales la función es 0.
\ [\ begin (matriz) (| c | c | c | c | c | c | c | c | c |) \ hline x & y & z & \ overline y & x \ wedge \ overline y & x \ wedge \ overline y \ wedge z & \ overline x & \ overline x \ vee y & x \ wedge \ overline y \ wedge z \ vee \ overline x \ vee y \\ \ hline 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ \ hline 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 y 1 \\ \ hline \ end (matriz) \]
1. \ (x \ rightarrow y \) = \ (\ overline x \ vee y. \)
2. Note que para \ (y = 1 \) \ (F = 1, \) ya que la disyunción es verdadera si al menos una expresión incluida en ella es verdadera (líneas 3-4, 7-8 en la tabla de verdad). De manera similar, para \ (\ overline x = 1, \) es decir, para \ (x = 0, \) \ (F = 1 \) (líneas 1-4).
3. Para \ (x = 1 \) y \ (y = 0 \) \ (\ overline x \ vee y = 0, \) \ (x \ wedge \ overline y = 1. \) Para \ (z = 1 \) \ (x \ cuña \ overline y \ cuña z = 1 \) y \ (F = 1, \) ya que una de las expresiones (línea 6) es verdadera, y para \ (z = 0 \) \ (x \ cuña \ overline y \ cuña z = 0 \) y \ (F = 0, \) ya que ambas expresiones incluidas en la disyunción son falsas (línea 5).
De acuerdo con la tabla de verdad construida, vemos que para un conjunto \ ((x, \) \ (y, \) \ (z) \) \ (F = 0. \)
Respuesta 1
Tarea 3 # 10052
La función lógica \ (F \) viene dada por la expresión:
\ ((\ overline (z \ vee \ overline y)) \ vee (w \ wedge (z \ equiv y)) \)
Haz su tabla de la verdad. Como respuesta, ingrese la suma de los valores \ (z, \) \ (y \) y \ (w, \) para los cuales \ (F = 1. \)
\ [\ begin (matriz) (| c | c | c | c | c | c | c | c | c |) \ hline w & y & z & \ overline y & z \ vee \ overline y & \ overline ( z \ vee \ overline y) & z \ equiv y & w \ wedge (z \ equiv y) & \ overline z \ vee \ overline y \ vee w \ wedge (z \ equiv y) \\ \ hline 0 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ \ hline 0 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \ hline 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ \ hline 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 & 1 & 0 & 1 & 1 & 1 \\ \ hline \ end (matriz) \]
1. \ ((\ overline (z \ vee \ overline y)) = \ overline z \ wedge y \)
2. La tabla de verdad tendrá \ (2 ^ 3 = 8 \) líneas.
3. Si \ (z = 1 \) y \ (y = 1, \) \ (entonces (z \ equiv y) = 1 \) (ya que la equivalencia es verdadera si y solo si ambas declaraciones son simultáneamente falsas o verdaderas) ... \ (\ overline z \ wedge y = 0 \) \ ((0 \ wedge 1 = 0). \) Si \ (w = 1, \) \ (w \ wedge (z \ equiv y) = 1 \) \ ((1 \ wedge 1 = 1) \) y \ (F = 1, \) ya que la disyunción es verdadera si al menos uno de los enunciados incluidos en ella es verdadero (línea 8 en la tabla de verdad). Si \ (w = 0, \) \ (w \ wedge (z \ equiv y) = 0 \) \ ((0 \ wedge 1 = 0) \) y \ (F = 0, \) ya que ambas declaraciones, incluidas en la disyunción son falsas (línea 4).
4. De manera similar para \ (z = 0, y = 0. \) \ ((z \ equiv y) = 1, \) \ (\ overline z \ wedge y = 0 \) \ ((1 \ wedge 0 = 0 ). \) Entonces, nuevamente, el valor de la función dependerá de \ (w. \) Para \ (w = 1 \) \ (w \ cuña (z \ equiv y) = 1, \)\ (F = 1, \) ya que uno de los enunciados incluidos en la disyunción es verdadero (línea 5), y para \ (w = 0 \) \ (w \ cuña (z \ equiv y) = 0, \)\ (F = 0, \) ya que todas las afirmaciones son falsas (línea 1).
5. Si \ (z = 0 \) y \ (y = 1, \) entonces \ (\ overline z \ wedge y = 1 \) \ ((1 \ wedge 1 = 1). \) Dado que \ ((z \ equiv y) = 0 \) (después de todo, los valores \ (z \) y \ (y \) son diferentes), será falso para cualquier \ (w. \) Entonces, dado que el valor de \ La variable (w \) no afectará el valor de la función, ya que \ (z = 0 \) y \ (y = 1 \) \ (w \) puede ser 0 o 1. \ (F = 1, \ ) ya que uno de los enunciados incluidos en disyunción, verdadero (líneas 3, 7).
6. Si \ (z = 1 \) y \ (y = 0, \) entonces \ (\ overline z \ wedge y = 0 \ wedge 0 = 0. \) Dado que \ ((z \ equiv y) = 0, \) \ (w \ cuña (z \ equiv y) = w \ cuña 0 \) será falso para cualquier \ (w \) (es decir, \ (w \) puede ser 0 y 1). Por lo tanto, para \ (z = 1 \) y \ (y = 0 \) \ (F \) siempre será falso (ya que ambos enunciados incluidos en la disyunción son falsos, líneas 2, 5).
7. \ (F = 1 \) para los siguientes conjuntos \ (z, \) \ (y, \) \ (w: \) (0, 0, 1), (0, 1, 1), (1, 1, 1), (0, 1, 0). Si sumamos los valores, obtenemos 7.
Respuesta: 7
Misión 4 # 10053
La función lógica \ (F \) viene dada por la expresión:
\ (a \ wedge ((\ overline (b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a)) \)
Haz su tabla de la verdad. Como respuesta, ingrese la suma de los valores \ (a, \) \ (b \) y \ (c, \) para los cuales \ (F = 1. \)
\ [\ begin (matriz) (| c | c | c | c |) \ hline a & b & c & F \\\ hline 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 \ \ \ hline 0 & 1 & 0 & 0 \\ \ hline 0 & 1 & 1 & 0 \\ \ hline 1 & 0 & 0 & 1 \\ \ hline 1 & 0 & 1 & 1 \\ \ hline 1 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 \\ \ hline \ end (matriz) \]
1. En la tabla de verdad \ (2 ^ 3 = 8 \) líneas.
2. Para \ (a = 0 \) \ (F = 0 \) para cualquier valor \ (b \) y \ (c, \) ya que la conjunción es verdadera si y solo si todas las declaraciones incluidas en ella son verdaderas (líneas 1-4 en la tabla de verdad).
3. Considere los casos en los que \ (a = 1. \) Si \ (\ overline ((b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a) = 1, \) entonces \ (F = 1 \) (ya que ambas declaraciones serán verdaderas), de lo contrario \ (F = 0 \) (ya que una declaración será falsa). Ley de de Morgan \ (\ overline (b \ wedge c) = \ overline b \ vee \ overline c. \) Entonces, teniendo en cuenta que \ (a = 1, \) \ (\ overline ((b \ wedge c)) \ vee (a \ wedge \ overline b) \ vee (\ overline c \ wedge a) = \ overline b \ vee \ overline c \ vee \ overline b \ vee \ overline c = \ overline b \ vee \ overline c. \)
4. Si \ (\ overline b = 0 \) y \ (\ overline c = 0 \) (simultáneamente, es decir, para \ (b = 1 \) y \ (c = 1), \) entonces \ (\ overline b \ vee \ overline c = 0 \) y \ (F = 0 \) (línea 8). En otros casos \ (\ overline b \ vee \ overline c = 1 \) y \ (F = 1 \) (líneas 5-7).
5. Los conjuntos \ ((x, \) \ (y, \) \ (z), \) para los cuales \ (F = 1: \) (1, 0, 0), (1, 1, 0), (1, 0, 1). La suma de los valores es 5.
Respuesta: 5
Tarea 5 # 10054
La función lógica \ (F \) viene dada por la expresión:
\ (((a \ wedge b) \ vee (b \ wedge c)) \ equiv ((d \ rightarrow a) \ vee (b \ wedge \ overline c)) \)
Haz una tabla de la verdad. Como respuesta, ingrese la suma de los valores \ (a, \) para los cuales \ (F = 0. \)
\ [\ begin (matriz) (| c | c | c | c | c |) \ hline a & b & c & d & F \\\ hline 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 0 & 1 & 1 \\ \ hline 0 & 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 1 & 1 & 0 \\ \ hline 1 & 0 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 & 1 \\ \ hline 1 & 1 & 1 & 0 & 1 \\ \ hline 1 & 1 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 & 0 \\ \ hline 1 & 1 & 0 & 1 & 1 \\ \ hline 1 & 0 & 1 & 0 & 0 \\ \ hline 1 & 0 & 0 & 1 & 0 \\ \ hline 0 & 1 & 1 & 0 & 1 \\ \ hline \ end (array) \]
1. Según la ley de distribución \ ((a \ cuña b) \ vee (b \ cuña c) = b \ cuña (a \ vee c). \)
2. \ (d \ rightarrow a = \ overline d \ vee a. \)
3. \ (((a \ wedge b) \ vee (b \ wedge c)) \ equiv ((d \ rightarrow a) \ vee (b \ wedge \ overline c)) = b \ wedge (a \ vee c) \ equiv (\ overline d \ vee a \ vee (b \ wedge \ overline c)). \)
4. Si \ (b = 0, \) entonces el lado izquierdo de la función es igual a 0 \ ((0 \ wedge (a \ vee c) = 0). \) \ (b \ wedge \ overline c = 0 \ wedge \ overline c = 0. \) Esto significa que para \ (b = 0 \) \ (c \) puede ser cualquier cosa, ya que no afecta el valor de la función. \ (F = 1, \) if \ (\ overline d \ vee a = 0 \) (entonces una de las expresiones incluidas en la disyunción será verdadera). Esto se hace con \ (\ overline d = 0 \) \ ((d = 1) \) y \ (a = 0 \) (líneas 2, 3). Para otros \ (d \) y \ (a \) \ (\ overline d \ vee a = 0, \) significa \ (F = 0, \) ya que la operación de equivalencia es verdadera si y solo si ambos enunciados son simultáneamente verdadero o falso (líneas 1, 10 en la tabla de verdad).
5. Si \ (b = 1, \) entonces \ (b \ cuña (a \ vee c) = 1 \ cuña (a \ vee c) = a \ vee c. \) \ (b \ wedge \ overline c = 1 \ wedge \ overline c = \ overline c. \) Entonces tenemos eso \ (a \ vee c \ equiv \ overline d \ vee a \ vee \ overline c. \) Si \ (a = 1, \) entonces \ (a \ vee c = 1 \) y \ (\ overline d \ vee a \ vee \ overline c = 1, \) ya que la disyunción es verdadera si al menos una de las expresiones es verdadera (y ambas disyunciones contienen \ (a = 1). \) Entonces, si \ (b = 1 \) y \ (a = 1, \) \ (F = 1 \) para cualquier \ (c \) y \ (d \) (líneas 5, 7, 8, 11).
Si \ (a = 0, \) entonces \ (a \ vee c = 0 \ vee c = c, \) y \ (\ overline d \ vee a \ vee \ overline c = \ overline d \ vee \ overline c. \) Tenemos: \ (c \ equiv (\ overline d \ vee \ overline c). \) Para \ (c = 1 \) \ (1 \ equiv \ overline d. \) Para \ (d = 1 \) \ (F = 0, \) dado que las declaraciones son diferentes (línea 4), para \ (d = 0 \) \ (F = 1, \) ya que ambas afirmaciones son verdaderas (línea 14). Para \ (c = 0 \) \ (0 \ equiv (\ overline d \ vee 1). \) Dado que \ (\ overline d \ vee 1 \) es una disyunción en la que uno de los enunciados es verdadero, toda la disyunción también es verdadera. Entonces \ (0 \ equiv 1, \) que no es cierto, lo que significa \ (F = 0 \) para cualquier \ (d \) (líneas 9, 16).
Según la tabla construida, vemos que \ (F = 0 \) para \ (a = 0 \) (líneas 1, 4, 9, 10, 16) y para \ (a = 1 \) (líneas 6, 12 , 13, 15). Entonces la suma de los valores es 0 * 5 + 1 * 4 = 4.
Respuesta: 4
Tarea 6 # 10055
La función lógica \ (F \) viene dada por la expresión:
\ ((a \ equiv (b \ vee \ overline c)) \ rightarrow (c \ wedge (b \ vee a)) \)
Haz una tabla de la verdad. Como respuesta, ingrese la suma de los valores \ (c, \) para los cuales \ (F = 1. \)
\ [\ begin (matriz) (| c | c | c | c |) \ hline a & b & c & F \\\ hline 0 & 0 & 0 & 1 \\ \ hline 0 & 0 & 1 & 0 \ \ \ hline 0 & 1 & 1 & 1 \\ \ hline 0 & 1 & 0 & 1 \\ \ hline 1 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 0 \\ \ hline 1 & 1 & 1 & 1 \\ \ hline 1 & 0 & 1 & 1 \\ \ hline \ end (matriz) \]
La tabla contiene \ (2 ^ 3 = 8 \) filas.
1. Una implicación es falsa si y solo si se sigue falso de un enunciado verdadero. Por lo tanto, \ (F = 0, \) si a \ (c \ wedge (b \ vee a) = 0. \) En otros casos \ (F = 1. \) Considere para qué valores \ (a, \ ) \ (b \) y \ (c \) \ (a \ equiv (b \ vee \ overline c) = 1 \)(si \ (a \ equiv (b \ vee \ overline c) = 0, \) entonces \ (F = 1 \) para cualquier valor \ (c \ wedge (b \ vee a) = 0). \)
Si \ (a = 0, \) entonces ejecutar \ (a \ equiv (b \ vee \ overline c) = 1, \) necesario \ (b \ vee \ overline c = 0 \) (después de todo, la operación de equivalencia es verdadera si y solo si ambas declaraciones son verdaderas o ambas son falsas). Para que la disyunción \ ((b \ vee \ overline c) \) sea falsa, ambas declaraciones incluidas en ella deben ser falsas, es decir, \ (b = 0 \) y \ (\ overline c = 0 \) \ ( (c = 1). \) Para tales valores \ (c \ cuña (b \ vee a) = 1 \ cuña (0 \ vee 0) = 0. \) Luego \ ((a \ equiv (b \ vee \ overline c)) \ rightarrow (c \ wedge (b \ vee a)) = 1 \ rightarrow 0 = 0, \)\ (F = 0. \) Esto corresponde a la línea 2 de la tabla de verdad.
Si \ (a = 1, \) entonces ejecutar \ (a \ equiv (b \ vee \ overline c) = 1, \)\ (b \ vee \ overline c = 1. \) Esto se hace en varios casos. Si \ (b = 1, \) entonces \ (c \) puede ser igual a cero y uno, porque uno de los enunciados incluidos en la disyunción ya es verdadero. Para \ (c = 1 \) \ (c \ cuña (b \ vee a) = 1 \ cuña 1 = 1, \) luego \ (F = 1 \) (ya que \ (1 \ rightarrow 1 = 1, \) línea 7). Para \ (c = 0 \) \ (c \ cuña (b \ vee a) = 0 \ cuña 1 = 0, \) por lo tanto, \ (F = 0 \) \ ((1 \ rightarrow 0 = 0, \) línea 6). Si \ (b = 0, \) entonces \ (\ overline c = 1 \) \ ((c = 0, \) entonces una de las afirmaciones incluidas en la disyunción será verdadera). En este caso \ (c \ cuña (b \ vee a) = 0 \ cuña (0 \ vee 1) = 0. \)\ (F = 0, \) ya que \ (1 \ rightarrow 0 = 0 \) (línea 5).
2. Para otros valores \ (a, \) \ (b \) y \ (c \) \ (F = 1, \) porque \ (a \ equiv (b \ vee \ overline c) = 0 \)(líneas 1, 3, 7, 8).
3. De la tabla de verdad compilada vemos que \ (F = 1 \) para \ (c = 0 \) (líneas 1, 4) y para \ (c = 1 \) (líneas 3, 7, 8). La suma de los valores es 0 * 2 + 1 * 3 = 3. \ (2 ^ 4 = 16 \) líneas.
1. Dado que la conjunción es falsa, si al menos uno de los enunciados es falso, entonces para \ (d = 0 \) \ (F = 0 \) para cualquier \ (a, \) \ (b \) y \ ( c \) (líneas 1, 6-10, 12, 14 en la tabla de verdad).
2. Considere el caso cuando \ (d = 1. \) Entonces \ ((a \ rightarrow b) \ wedge (b \ equiv c) \ wedge d = (a \ rightarrow b) \ wedge (b \ equiv c) \ wedge 1 = (a \ rightarrow b) \ wedge (b \ equiv C). \) Para \ (b = 1 \) \ (a \ rightarrow b = a \ rightarrow 1 = 1 \) para cualquier \ (a, \) ya que la implicación es falsa si y solo si se sigue falso de un enunciado verdadero. Si \ (c = 1, \) entonces \ (b \ equiv c = 1, \) ya que la operación de equivalencia es verdadera cuando ambas expresiones son verdaderas o ambas son falsas, y \ (F = 1 \) (ya que todas las expresiones incluyen en conjunción son verdaderas). Esto corresponde a las líneas 4 y 5. Si \ (c = 0, \) entonces \ (b \ equiv c = 0, \) \ (F = 0, \) ya que una de las expresiones incluidas en la conjunción es falsa (líneas 11 y 16).
Para \ (b = 0: \) si \ (a = 1, \) entonces \ (a \ flecha derecha b = 1 \ flecha derecha 0 = 0, \) entonces una de las expresiones incluidas en la conjunción es falsa, y \ (F = 0 \) para cualquier \ (c \) (líneas 13 y 15). Si \ (a = 0, \) entonces \ (a \ rightarrow b = 0 \ rightarrow 0 = 1. \) Si \ (c = 0, \) entonces \ (b \ equiv c = 0 \ equiv 0 = 1, \)\ (F = 1, \) ya que ambas expresiones incluidas en la conjunción son verdaderas (línea 2). Si \ (c = 1, \) entonces \ (b \ equiv c = 0 \ equiv 1 = 0, \)\ (F = 0, \) ya que una de las expresiones incluidas en la conjunción es falsa (línea 3).
Por lo tanto, \ (F = 1 \) para \ (d = 1 \) (líneas 2, 4, 5). La suma de los valores \ (d \) es 1 * 3 = 3.
Construcción de tablas de verdad para enunciados complejos.
Prioridad booleana
1) inversión 2) conjunción 3) disyunción 4) implicación y equivalencia
¿Cómo hacer una tabla de verdad?
Por definición, la tabla de verdad de una fórmula lógica expresa la correspondencia entre varios conjuntos de valores de variables y los valores de una fórmula.
Para una fórmula que contiene dos variables, solo hay cuatro conjuntos de valores de variable de este tipo:
(0, 0), (0, 1), (1, 0), (1, 1).
Si una fórmula contiene tres variables, entonces hay ocho posibles conjuntos de valores de variables (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1) , (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
El número de conjuntos de una fórmula con cuatro variables es dieciséis, y así sucesivamente.
Una forma conveniente de notación para encontrar los valores de una fórmula es una tabla que contiene, además de los valores de las variables y los valores de la fórmula, también los valores de las fórmulas intermedias.
Ejemplos.
1. Creemos una tabla de verdad para la fórmula 96% "style =" width: 96.0% ">
La tabla muestra que para todos los conjuntos de valores de las variables xey, la fórmula toma el valor 1, es decir, es idénticamente cierto.
2. Tabla de verdad para la fórmula 96% "style =" width: 96.0% ">
La tabla muestra que para todos los conjuntos de valores de las variables xey, la fórmula toma el valor 0, es decir, es idénticamente falso .
3. Tabla de verdad para la fórmula 96% "style =" width: 96.0% ">
La tabla muestra que fórmula 0 "style =" border-collapse: collapse; border: none ">
Conclusión: tenemos todas las unidades en la última columna. Esto significa que el significado de un enunciado complejo es verdadero para cualquier valor de enunciados simples K y C. Por lo tanto, el maestro razonó lógicamente correctamente.
 Gestión y funciones del mod No hay suficientes artículos
Gestión y funciones del mod No hay suficientes artículos Solución de problemas de TLauncher
Solución de problemas de TLauncher ¿Por qué Instagram no busca la ubicación: las principales razones?
¿Por qué Instagram no busca la ubicación: las principales razones? Cómo borrar el caché en la aplicación vk
Cómo borrar el caché en la aplicación vk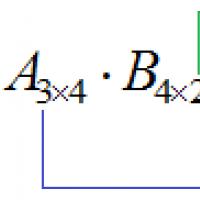 Operaciones básicas sobre matrices (suma, multiplicación, transposición) y sus propiedades
Operaciones básicas sobre matrices (suma, multiplicación, transposición) y sus propiedades Baterías de polímero de litio
Baterías de polímero de litio Conversiones idénticas de expresiones lógicas
Conversiones idénticas de expresiones lógicas