Traer a un formulario escalonado con la solución. Cortar la matriz a una forma escalonada. Filas elementales y transformaciones de columnas. Criterio de dependencia lineal de los vectores.
Para llevar la matriz a un tipo escalonado (Fig. 1.4), debe realizar los siguientes pasos.
1. En la primera columna, seleccione un elemento que no sea cero ( elemento de plomo ). Una cadena con un elemento líder ( cadena principal ) Si no es el primero, reorganizar en la primera línea (conversión I tipo). Si no hay maestría en la primera columna (todos los elementos son cero), no excluimos esta columna y continuamos buscando el elemento de plomo en el resto de la matriz. La conversión termina si todas las columnas están excluidas o en la parte restante de la matriz todos los elementos cero.
2. Divida todos los elementos de la cadena de host al elemento de plomo (transformación tipo II). Si la línea principal es la última, entonces, en esta transformación debe terminarse.
3. A cada fila ubicada debajo del cable, agregue una línea líder multiplicada por un número de este tipo, respectivamente, de modo que los elementos que se encuentran debajo del cable sean iguales a cero (transformación Tipo III).
4. Al eliminar la línea y la columna de la consideración, en cuya intersección es el elemento líder, vaya a la cláusula 1, en la que todas las acciones descritas se aplican al resto de la matriz.
7. El teorema es sobre la fila de una fila de una fila de elementos elementales.
El teorema de definición para los elementos de una cadena o columna le permite reducir el cálculo del determinante - ordenar () calcular los determinantes del procedimiento. .
Si el determinante tiene elementos iguales de cero, entonces el más conveniente para descomponer el determinante para los elementos de la fila o columna, que contiene el mayor número de ceros.
Usando las propiedades de los determinantes, puede convertir el determinante - el pedido para que todos los elementos de alguna fila o columna, excepto uno, se vuelvan iguales a cero. Así, el cálculo del determinante. - orden, si es diferente de cero, se reducirá al cálculo de un determinante - pedido.
Tarea 3.1.Calcular el determinante
Decisión. Agregar la primera línea primero, al tercero, la primera, multiplicada por 2, a la cuarta, la primera, multiplicada por -5, obtenemos
Descomposición del determinante para los elementos de la primera columna, tenemos
En el determinante resultante de la tercera orden, nos convierte en cero todos los elementos de la primera columna, excepto el primero. Para hacer esto, la segunda línea agregará la primera, multiplicada por (-1), a la tercera, multiplicada por 5, agregará la primera, multiplicada por 8. Dado que la tercera línea se multiplicó por 5, entonces (para que el Determinante no cambiar) para multiplicarlo. Tengo
El determinante resultante se descompondrá en los elementos de la primera columna:
8. Teorema de Laplace (1). Teorema sobre Stranki DopName (2)
1) Identifica la determinación de los elementos de cualquier fila en su IAalgebracy.
2) El resumen de los elementos del determinante para los suplementos algebraicos de los elementos correspondientes de la otra línea es cero (el teorema de la multiplicación en los suplementos algebraicos de otras personas).
9. Vector aritmético cariño.
Cualquier punto en el plano bajo el sistema de coordenadas seleccionado es dado por un par (α, β) de sus coordenadas; Los números α y β también pueden entenderse como las coordenadas del vector de radio con el fin en este punto. De manera similar, en el espacio Troika (α, β, γ) determina el punto o vector con las coordenadas α, β, γ. Esto se basa en un lector conocido la interpretación geométrica de los sistemas de ecuaciones lineales con dos o tres incógnitas. Entonces, en el caso de un sistema de dos ecuaciones lineales con dos desconocidas.
un 1 x + b 1 y \u003d c 1,
a 2 X + B 2 Y \u003d C 2
cada una de las ecuaciones se interpreta tan recta en el plano (ver Fig. 26), y la solución (α, β) es como un punto de intersección de estos directos o como un vector con las coordenadas de aire (la cifra corresponde al caso cuando El sistema tiene una sola solución).
Higo. 26.
De manera similar, puede inscribirse con el sistema de ecuaciones lineales con tres desconocidas, interpretando cada ecuación como la ecuación del plano en el espacio.
En las matemáticas y varias aplicaciones (en particular, en la teoría de la codificación), es necesario lidiar con los sistemas de ecuaciones lineales que contienen más de tres desconocidas. El sistema de ecuaciones lineales con n desconocido x 1, x 2, ..., x n se llama un conjunto de ecuaciones de la especie.
un 11 x 1 + a 12 x 2 + ... + y 1n x n \u003d b 1,
a 21 x 1 + A 22 x 2 + ... + A 2N X N \u003d B 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
y m1 x 1 + y m2 x 2 + ... + y mn x n \u003d b m,
donde un IJ y B i son números válidos arbitrarios. El número de ecuaciones en el sistema puede ser cualquiera y no está asociado con el número de desconocido. Los coeficientes en desconocidos y IJ tienen una doble numeración: el primer índice que indica el número de la ecuación, el segundo índice J es el número de lo desconocido, que cuesta este coeficiente. Cualquier solución del sistema se entiende como un conjunto (válido) de los valores de desconocido (α 1, α 2, ..., α n), energizando cada ecuación en igualdad fiel.
Aunque la interpretación geométrica directa del sistema (1) en N\u003e 3 ya no es posible, pero es bastante posible y, en muchos sentidos, es conveniente extenderse a un lenguaje arbitrario N geométrico del espacio de dos o tres dimensiones. Este objetivo y sirve definiciones adicionales.
Cualquier conjunto ordenado de N números válidos (α 1, α 2, ..., α n) se denomina vector aritmético N-dimensional, y los números α 1, α 2, ..., α n coordenadas de este vector.
Para la designación de vectores, se usa, como regla general, audaz y para el vector A con las coordenadas α 1, α 2, ..., α n se conserva forma ordinaria Registros:
a \u003d (α 1, α 2, ..., α n).
Por analogía con un plano convencional, el conjunto de todos los vectores n-dimensionales que satisfacen la ecuación lineal con n desconocidos se denomina hiperplano en el espacio n-dimensional. Con esta definición, el conjunto de todas las soluciones del sistema (1) no es más que la intersección de varios hiperplanos.
La adición y la multiplicación de los vectores n-dimensionales están determinados por las mismas reglas que para los vectores convencionales. A saber, si
a \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Dos vector n-dimensional, luego su suma se llama vector.
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
El producto del vector y el número λ se llama vector.
λа \u003d (λα 1, λα 2, ..., λα n). (cuatro)
El conjunto de todos los vectores aritméticos n-dimensionales con las operaciones de la adición de vectores y la multiplicación del vector se llama un espacio vectorial n-dimensional aritmético l n.
Usando las operaciones ingresadas, es posible considerar combinaciones lineales arbitrarias de varios vectores, es decir, la expresión
λ 1 A 1 + λ 2 A 2 + ... + λ k a k,
donde λ i es un número válido. Por ejemplo, una combinación lineal de vectores (2) con coeficientes λ y μ es un vector
λа + μB \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
En el espacio tridimensional de los vectores, la parte superior de los vectores I, J, k (Ortops de coordenadas) desempeñan un papel especial, que se descompone por cualquier vector A:
a \u003d xi + yj + zk,
donde X, Y, Z son números válidos (las coordenadas del vector A).
En caso n-dimensional, los siguientes vectores desempeñan el mismo papel:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Cada vector A es, obviamente, una combinación lineal de vectores E 1, E 2, ..., E n:
a \u003d A 1 E 1 + A 2 E 2 + ... + A N E N, (6)
además, los coeficientes α 1, α 2, ..., α n coinciden con las coordenadas del vector a.
Denote por 0 Vector, todas las coordenadas de las cuales son cero (brevemente, cero vector), introducimos la siguiente definición importante:
El sistema de vectores A 1, y 2, ... y K se llama lineal dependiente, si hay una combinación lineal de vector igual.
λ 1 A 1 + λ 2 A 2 + ... + λ k a k \u003d 0,
en el que al menos uno de los coeficientes H 1, λ 2, ..., λ k es diferente de cero. De lo contrario, el sistema se llama linealmente independiente.
Entonces, vectores
a 1 \u003d (1, 0, 1, 1), A 2 \u003d (1, 2, 1, 1), y 3 \u003d (2, 2, 2, 2)
depende linealmente porque
a 1 + A 2 - A 3 \u003d 0.
La dependencia lineal, como se puede ver en la definición, es equivalente (en K ≥ 2) al hecho de que al menos uno de los vectores del sistema es una combinación lineal de los restantes.
Si el sistema consta de dos vectores a 1, A 2, entonces la dependencia lineal del sistema significa que uno de los vectores es proporcional a otro, por ejemplo, y 1 \u003d λa 2; En un caso tridimensional, es equivalente a la colinealidad de los vectores A 1 y A 2. De manera similar, la dependencia lineal del sistema I de tres vectores en el espacio convencional significa la compatación de estos vectores. Concepto dependencia lineal Por lo tanto, es la generalización natural de los conceptos de colinealidad y comparidad.
Es fácil asegurarse de que los vectores E 1, E 2, ..., E n del sistema (5) son linealmente independientes. Por lo tanto, hay sistemas de los vectores linealmente independientes en el espacio n-dimensional. Se puede demostrar que cualquier sistema de mayor número de vectores depende linealmente.
Cualquier sistema A 1, A 2, ... y N de n vectores independientes linealmente independientes del espacio n-dimensional L n se llama su base.
Cualquier vector y los espacios l n se despliega, y además, por el vector de una base arbitraria a 1, y 2, ..., y N:
a \u003d λ 1 A 1 + λ 2 A 2 + ... + λ n A n.
Este hecho se establece fácilmente en función de la definición de la base.
Continuando una analogía con un espacio tridimensional, es posible en el caso n-dimensional determinar el producto escalar A · B de vectores, creyendo
a · b \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
Con esta definición, se conservan todas las propiedades básicas del producto escalar de los vectores tridimensionales. Los vectores A y B se llaman ortogonal si su producto escalar es cero:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
En la teoría de los códigos lineales, se usa otro concepto importante: el concepto de subespacio. El subconjunto del espacio V L N se llama subespacio de este espacio si
1) Para cualquier vectores A, B, pertenecientes a V, su suma A + B también pertenece a V;
2) Para cualquier vector A, perteneciente a V, y para cualquier número real λ, el vector λa también pertenece a V.
Por ejemplo, el conjunto de todas las combinaciones lineales de vectores E 1, E 2 del sistema (5) será un subespacio del espacio l n.
En un álgebra lineal, se demuestra que en cada subespacio V, hay un sistema de vectores tan linealmente independiente A 1, A 2, ..., un k, que cada vector y subespacio es una combinación lineal de estos vectores:
a \u003d λ 1 A 1 + λ 2 A 2 + ... + λ k a k.
El sistema de vectores especificado se llama la base del subespacio V.
Desde la definición del espacio y el subespacio sigue inmediatamente que el espacio L N es el grupo conmutativo en relación con la formación de vectores, y cualquiera de sus subespacio V es un subgrupo de este grupo. En este sentido, es posible, por ejemplo, considerar las clases adyacentes del espacio L N por subespacimiento V.
En conclusión, enfatizamos que si en la teoría del espacio aritmético n-dimensional en lugar de números válidos (es decir, los elementos del campo de los números válidos) consideran los elementos de un campo arbitrario F, luego todas las definiciones y los hechos dados anteriormente. habría conservado fuerza.
En la teoría de la codificación, un rol importante desempeña el caso cuando el campo F campo de deducción Z P, que, como sabemos, por supuesto. En este caso, el espacio n-dimensional correspondiente también contiene, ya que no es difícil ver, los elementos P N.
El concepto de espacio, así como el concepto de un grupo y anillos, también permite una definición axiomática. Para obtener más información, enviamos al alimentador a cualquier curso de un álgebra lineal.
10. Lynіin Combіnatsiya. Vector del sistema Inepless Lynіino Zarezhnі Tu.
En este tema, considere el concepto de la matriz, así como los tipos de matrices. Ya que hay muchos términos en este tema, agregaré resumenPara navegar en el material fue más fácil.
Definición de la matriz y su elemento. Designaciones.
La matriz - Esta es una tabla de $ m $ filas y columnas de $ n $. Los objetos de la matriz pueden ser objetos de una naturaleza completamente diversa: números, variables o, por ejemplo, otras matrices. Por ejemplo, la matriz de $ \\ izquierda (\\ comienzan (matriz) (CC) 5 y 3 \\\\ 0 y -87 \\\\ 8 & 0 \\ Fin (Array) \\ Derecha) $ contiene 3 líneas y 2 columnas; Sus elementos son enteros. Matrix $ \\ Izquierda (\\ Begin (Array) (CCCC) A & A ^ 9 + 2 y 9 y Sin X \\\\ -9 & 3T ^ 2-4 & UT & 8 \\ FIN (Array) \\ Derecha) $ Contiene 2 Líneas y 4 columnas.
Diferentes formas de grabar matrices: Mostrar / Ocultar
La matriz se puede grabar no solo en la ronda, sino también en corchetes cuadrados o dobles directos. A continuación se muestra la misma matriz en varias formas de grabación:
$$ \\ izquierda (\\ comienzan (matriz) (CC) 5 y 3 \\\\ 0 \\ 8 & -87 \\\\ 8 &-0 \\ Fin (Array) \\ Derecha); \\; \\; \\ izquierda [\\ comienzan (matriz) (CC) 5 y 3 \\\\ 0 y -87 \\\\ 8 & 0 \\ Fin (Array) \\ Derecha]; \\; \\; \\ Izquierda \\ VERT \\ Comenzar (Array) (CC) 5 y 3 \\\\ 0 & -87 \\\\ 8 & 0 \\ FIN (Array) \\ Derecha \\ Vert $$
El producto $ m \\ veces n $ se llama el tamaño de la matriz. Por ejemplo, si la matriz contiene 5 líneas y 3 columnas, dicen sobre la matriz del tamaño de $ 5 \\ veces $ 3. MATRIX $ \\ izquierda (\\ comienzan (matriz) (CC) 5 y 3 \\\\ 0 \\ 0 & -87 \\\\ 8 y 0 \\ FIN (Array) \\ Derecha) $ tiene un tamaño de $ 3 \\ veces $ 2.
Típicamente, las matrices son designadas por las letras grandes del alfabeto latino: $ A $, $ B $, $ C $, etc. Por ejemplo, $ b \u003d \\ izquierda (\\ comienzan (matriz) (CCC) 5 y 3 \\\\ 0 y -87 \\\\ 8 & 0 \\ FIN (Array) \\ Derecha) $. La numeración de cadenas está rematada; Columnas - de izquierda a derecha. Por ejemplo, la primera línea de la matriz de $ b $ contiene elementos 5 y 3, y la segunda columna contiene elementos 3, -87, 0.
Los elementos de las matrices generalmente se denotan por letras pequeñas. Por ejemplo, los elementos de la matriz de $ A $ se denotan $ A_ (IJ) $. El índice dual $ ij $ contiene información sobre la posición del elemento en la matriz. El número $ I $ es el número de la línea, y el número $ J $ es el número de la columna, en la intersección, de la cual hay un elemento $ A_ (IJ) $. Por ejemplo, en la intersección de la segunda línea y la quinta columna de la matriz $ A \u003d \\ izquierda (\\ Begin (Array) (CCCCCC) 51 y 37 y -9 y 0 y 9 y 97 \\\\ 1 y 2 y 3 y 3 & 41 y 59 y 6 \\ \\ -17 y -15 y -5 \\\\ 52 & -8 & -5 \\\\ 52 y 33 y -4 & -1 & 17 y -4 & -1 & 17 & 90 \\ Fin (Array) \\ Derecha) $ Situado $ A_ (25) \u003d $ 59:
De la misma manera, en la intersección de la primera línea y la primera columna tenemos un elemento $ A_ (11) \u003d $ 51; En la intersección de la tercera fila y la segunda columna, el elemento $ A_ (32) \u003d - $ 15 y así sucesivamente. Observo que el registro $ A_ (32) $ se lee como "y tres dos", pero no "y treinta y dos".
Para la designación abreviada de la matriz $ A $, el tamaño del cual es $ m \\ veces n $, se utiliza para registrar $ A_ (M \\ Times N) $. Se usa a menudo y tal registro:
$$ A_ (M \\ Times (N)) \u003d (A_ (IJ)) $$
Aquí $ (A_ (IJ)) $ indica la designación de los elementos de la matriz $ A $, es decir, Sugiere que los elementos de la matriz de $ A $ se denominan $ A_ (IJ) $. En la forma de implementación de la matriz $ A_ (M \\ Times N) \u003d (A_ (IJ)) $ se puede escribir como:
$$ A_ (M \\ Times N) \u003d \\ IZQUIERDA (\\ BEGIN (Array) (CCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1N) \\\\ A_ (21) & A_ (22) & \\ LDOTS & A_ (2N) \\\\ \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS \\\\ A_ (M1) & A_ (M2) & \\ LDOTS & A_ (MN) \\ FIN (Array) \\ Derecha) $$
Introducimos otro término - matrices iguales.
Dos matrices del mismo tamaño $ A_ (M \\ Times N) \u003d (A_ (IJ)) $ y $ b_ (m \\ veces n) \u003d (b_ (ij)) $ llamado igualSi sus elementos respectivos son iguales, es decir, $ A_ (ij) \u003d b_ (ij) $ para todos los $ i \u003d \\ overline (1, M) $ y $ J \u003d \\ Overline (1, N) $.
Explicación del registro $ i \u003d \\ Overline (1, M) $: Mostrar / Ocultar
Grabación "$ i \u003d \\ Overline (1, M) $" significa que el parámetro $ I $ varía de 1 a m. Por ejemplo, el registro $ i \u003d \\ Overline (1.5) $ indica que el parámetro $ i $ toma valores 1, 2, 3, 4, 5.
Entonces, para la igualdad de matrices, se requiere la ejecución de dos condiciones: coincidencia del tamaño y la igualdad de los elementos correspondientes. Por ejemplo, la matriz $ A \u003d \\ izquierda (\\ comienzan (matriz) (CC) 5 y 3 \\\\ 0 y -87 \\\\ 8 & 0 \\ Fin (Array) \\ Derecha) $ no es igual a la matriz $ B \u003d \\ izquierda (\\ comienzan (matriz) (CC) 8 & -9 \\\\ 0 & -87 \\ FIN (Array) \\ Derecha) $ Porque la matriz de $ A $ tiene un tamaño de $ 3 \\ veces $ 2 y el $ B $ Matrix Tamaño es $ 2 \\ veces $ 2. Además, la matriz de $ A $ no es igual a la matriz de $ c \u003d \\ izquierda (\\ comienzan (matriz) (CC) 5 y 3 \\\\ 98 y -87 \\\\ 8 & -87 \\\\ 8 & 0 \\ Fin (Array) \\ Derecha ) $, desde $ A_ (21) \\ NEQ C_ (21) $ (es decir, $ 0 \\ NEQ $ 98). Pero para la matriz $ F \u003d \\ izquierda (\\ Comenzar (matriz) (CC) 5 y 3 \\ Ed (Array) \\ Derecha) $ puede grabar audazmente $ a \u003d F $ desde y dimensiones, y los elementos correspondientes de las matrices $ Un $ y $ F $ coincide.
Ejemplo №1
Determine el tamaño de la matriz $ A \u003d \\ Izquierda (\\ Begin (Array) (CCC) -1 & -2 & 1 \\\\ 5 y 9 & -8 \\\\ -6 y 8 y 23 \\\\ 11 & -12 & -5 \\ \\ 4 y 0 & -10 \\ FIN (Array) \\ Derecha) $. Indique lo que es igual a los elementos $ A_ (12) $, $ A_ (33) $, $ A_ (43) $.
Esta matriz contiene 5 líneas y 3 columnas, por lo que el tamaño de sus $ 5 \\ veces $ 3. Para esta matriz, también puede usar la designación $ A_ (5 \\ Times 3) $.
Un elemento $ A_ (12) $ está en la intersección de la primera línea y la segunda columna, por lo tanto, $ A_ (12) \u003d - $ 2. Un elemento $ A_ (33) $ está en la intersección de la tercera línea y la tercera columna, por lo tanto, $ A_ (33) \u003d 23 $. El elemento $ A_ (43) $ está en la intersección de la cuarta línea y la tercera columna, por lo tanto, $ A_ (43) \u003d - $ 5.
Respuesta: $ A_ (12) \u003d - 2 $, $ A_ (33) \u003d 23 $, $ A_ (43) \u003d - $ 5.
Tipos de matrices dependiendo de su tamaño. Inicio y diagonal lateral. Marca de matriz.
Deje una cierta matriz de $ A_ (M \\ Times N) $. Si $ m \u003d 1 $ (la matriz consta de una fila), entonces se llama la matriz especificada matriz-cadena. Si $ n \u003d 1 $ (la matriz consta de una columna), entonces se llama una matriz de una matriz. matriz-columna. Por ejemplo, $ \\ IZQUIERDA (\\ BEET (Array) (CCCCC) -1 & -2 & 0 & -9 & 8 \\ FIN (Array) \\ Derecha) $ - matrix-string, y $ \\ izquierda (\\ comienzan (Array ) (C) -1 \\\\ 5 \\\\ 6 \\ FIN (Array) \\ Derecha) $ - Matriz de columna.
Si la matriz $ A_ (M \\ Times N) $ es correcta a la condición de $ M \\ NE $ (es decir, el número de filas no es igual al número de columnas), a menudo se dice que $ A $ es un Matriz rectangular. Por ejemplo, la matriz de $ \\ izquierda (\\ comience (matriz) (CCCC) -1 y -2 y 0 y 9 \\\\ 5 y 9 y 5 y 1 \\ FIN (Array) \\ Derecha) $ tiene un tamaño $ 2 \\ Veces $ 4 esos. Contiene 2 líneas y 4 columnas. Dado que el número de filas no es igual al número de columnas, entonces esta matriz es rectangular.
Si para la matriz $ A_ (M \\ Times N) $, la condición es $ m \u003d n $ (es decir, el número de filas es igual al número de columnas), entonces dicen que $ A $ es una matriz cuadrada de alrededor de $ n $. Por ejemplo, $ \\ IZQUIERDA (\\ BEGIN (Array) (CC) -1 & -2 \\\\ 5 y 9 \\ FIN (Array) \\ Derecha) $ es una matriz cuadrada de segundo orden; $ \\ Izquierda (\\ Begin (Array) (CCC) -1 & -2 & 9 \\\\ 5 y 9 y -2 \\\\ 1 y 0 y 4 \\ End (Array) \\ Derecha) $ es una matriz cuadrada de tercer orden. En general, la matriz cuadrada $ A_ (n \\ veces n) $ se puede grabar así:
$$ A_ (n \\ veces N) \u003d \\ IZQUIERDA (\\ BEGIN (Array) (CCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1N) \\\\ A_ (21) & A_ (22) & \\ LDOTS & A_ (2N) \\\\ \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS \\\\ A_ (N1) & A_ (N2) & \\ LDOTS & A_ (NN) \\ FIN (Array) \\ Derecha) $$
Se dice que los elementos $ A_ (11) $, $ A_ (22) $, $ \\ LDOTS $, $ A_ (NN) $ están en diagonal principal MATRIX $ A_ (n \\ veces n) $. Estos elementos se llaman los principales elementos diagonales. (o simplemente elementos diagonales). Elements $ A_ (1N) $, $ A_ (2 \\; N-1) $, $ \\ LDOTS $, $ A_ (N1) $ están en lado (secundario) diagonal; se les llama elementos by-diagonales. Por ejemplo, para la matriz $ c \u003d \\ izquierda (\\ comience (matriz) (CCCC) 2 y 9 y 9 y 1 \\\\ 5 y 9 y 9 y 0 \\\\ 1 y 0 y 0 \\ \\ 1 y 4 y 6 \\ FIN (Array) \\ Derecha) $ Tenemos:

Elementos $ C_ (11) \u003d 2 $, $ C_ (22) \u003d 9 $, $ C_ (33) \u003d $ 4, $ C_ (44) \u003d $ 6 son los elementos diagonales principales; Elementos $ C_ (14) \u003d 1 $, $ C_ (23) \u003d $ 8, $ C_ (32) \u003d 0 $, $ C_ (41) \u003d - $ 4 - Elementos diagonales laterales.
La suma de los elementos diagonales principales se llama siguiendo la matriz y denota $ \\ tr A $ (o $ \\ SP A $):
$$ \\ tr a \u003d A_ (11) + A_ (22) + \\ LDOTS + A_ (NN) $$
Por ejemplo, para la matriz $ c \u003d \\ izquierda (\\ comienzan (Array) (CCCC) 2 & -2 y 9 y 1 \\\\ 5 y 9 y 8 y 0 \\\\ 1 y 0 y 4 & -7 \\\\ - 4 y 4 y -9 y 5 y 6 \\ FIN (Array) \\ Derecha) $ Tenemos:
$$ \\ tr c \u003d 2 + 9 + 4 + 6 \u003d 21. $$.
El concepto de elementos diagonales también se usa para las matrices no comerciales. Por ejemplo, para la matriz $ b \u003d \\ izquierda (\\ comienzan (Array) (CCCCC) 2 y 2 y 9 y 1 y 7 \\-5 y -9 y 0 y 4 & - 6 \\\\ 1 y 4 y 4 & - 7 & -6 \\ FIN (Array) \\ Derecha) $ Los elementos diagonales principales serán $ b_ (11) \u003d 2 $, $ b_ (22) \u003d - 9 $, $ b_ (33) \u003d $ 4.
Tipos de matrices dependiendo de los valores de sus elementos.
Si todos los elementos de la matriz $ A_ (M \\ Times N) $ son cero, entonces se llama una matriz de este tipo nulo Y generalmente se denota por la letra $ O $. Por ejemplo, $ \\ IZQUIERDA (\\ BEGE (Array) (CC) 0 y 0 \\\\ 0 y 0 \\ 0 \\ FIN (Array) \\ Derecha) $, $ \\ izquierda (\\ comience (matriz) (CCC) 0 y 0 \\\\ 0 & 0 \\ \\ ED (Array) \\ Derecha) $ - Matrices Cero.
Considere una cadena sin cero de la matriz de $ A $, es decir, Tal cadena en la que hay al menos un elemento distinto de cero. Elemento de plomo La línea distinta de cero lo llamará primero (contando de izquierda a derecha) un elemento distinto de cero. Por ejemplo, considere tal matriz:
$$ W \u003d \\ Izquierda (\\ Begin (Array) (CCCC) 0,099 0,099 0 \\ \\ \\\\ 0 € 0 € & 0 y 12 \\ Ed (Array) \\ Derecha) $ $ $
En la segunda línea, el plomo será el cuarto elemento, es decir,. $ w_ (24) \u003d 12 $, y en la tercera línea, el maestro será el segundo elemento, es decir, $ W_ (32) \u003d - $ 9.
MATRIX $ A_ (M \\ Times N) \u003d \\ IZQUIERDA (A_ (IJ) \\ Derecha) $ Llamado velocidadSi cumple con dos condiciones:
- Las líneas cero, si las hay, se encuentran debajo de todas las líneas distintas de cero.
- Los números de los elementos líderes de filas no cero forman una secuencia estrictamente creciente, es decir. Si $ A_ (1k_1) $, $ A_ (2k_2) $, ..., $ A_ (rk_R) $: los elementos líderes de líneas no cero de la matriz $ A $, luego $ k_1 \\ lt (k_2) \\ l \\ ldots \\ lt (k_r) $.
Ejemplos de matrices escalonadas:
$$ \\ Izquierda (\\ Begin (Array) (CCCCCC) (CCCCCC) 0 Homé Y '12 0 € AMS y 12. como y 03 y 039 0:0ODÓ como traducición 0 HAS \u003cbr\u003e 0 \u003cbr\u003e No 0 (0 ... MEX MUESME 40 &LAS Y H H H H H H H ... & 0 y 0 y 0 y 0 \\ Fin (Array) \\ Derecha); \\; \\ Izquierda (\\ Begin (Array) (CCCC) 5 & -2 y 2 & -8 \\\\ 0 y 4 y 0 y 0 \\ ed (Array) \\ Derecha). $$.
Para comparación: Matrix $ Q \u003d \\ Izquierda (\\ Begin (Array) (CCCCC) 2 y 0,099 y 0,0 y 0,099.ó No 0,09 y 0,099.ó No 0,0 y 0 ° y 0 y 0 y 0 y 0 y 0 y 0 y 0 y 0 y 10 y 10 y 10 y 10 & 6 \\ FIN (Array) \\ Derecha) $ no es un paso a paso, ya que la segunda condición se rompe en la determinación de la matriz escalonada. Los elementos líderes en la segunda y tercera línea $ Q_ (24) \u003d 7 $ y $ Q_ (32) \u003d $ 10 tienen números $ k_2 \u003d $ 4 y $ k_3 \u003d $ 2. Para una matriz escalonada, se debe realizar la condición $ k_2 \\ lt (k_3) $, que en este caso se deteriore. Observo que si cambia la segunda y tercera líneas en lugares, obtendremos una matriz escalonada: $ \\ izquierda (\\ comience (matriz) (CCCCC) 2 & -5 y 0 y 1 y 9 \\\\ 0 & -5 & 0 y 10 \\\\ 0,09 0,09 y 0 y 0 y 0 y 0 y 7 \\ FIN (Array) \\ Derecha) $.
Se llama una matriz escalonada trapezoidal o trapezoidalSi para los elementos líderes $ A_ (1k_1) $, $ A_ (2k_2) $, ..., $ A_ (RK_R) $ CONDICIONES DE $ K_1 \u003d 1 $, $ K_2 \u003d 2 $, ..., $ K_R \u003d R $, es decir, Los elementos diagonales están liderando. En general, la matriz trapezoidal se puede escribir de la siguiente manera:
$$ A_ (M \\ Times (N)) \u003d \\ IZQUIERDO (\\ BEGE (Array) (CCCCCC) A_ (11) & A_ (12) \\ LDOTS & A_ (1R) & \\ LDOTS & A_ (1N) \\\\ 0 & A_ (22) & \\ LDOTS & A_ (2R) \\ LDOTS & A_ (2N) \\\\ \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS \\\\ 0 & 0 & \\ LDOTS & A_ ( RR) \\ LDOTS & A_ (RN) \\\\ 0 & 0 & 0 \\ LDOTS & 0 & 0 & 0 \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS & \\ LDOTS \\\\ 0 & 0 \\ LDOTS & 0 & \\ LDOTS & 0 \\ FIN (Array) \\ Derecha) $$
Ejemplos de matrices trapezoidales:
$$ \\ Izquierda (\\ Begin (Array) 4 y 0ónico y 03 "y 039 vez y utis disponibilidad y 0 Cr deoto 4.0 7 259as 3 y_es mismooo 1300xtilu Masas.ó 7ove vez 1órico 0 y 0 y 0 \\\\ 0 \\ \\ \\ \\ 0,09 0,09 y 0 y 0 \\ \\ FIN (Array) \\ Derecha); \\; \\ Izquierda (\\ Begin (Array) (CCCC) 5 & -2 y 2 & -8 \\\\ 0 y 4 y 0 y 0 \\ ed (Array) \\ Derecha). $$.
Vamos a dar algunas definiciones más para matrices cuadradas. Si todos los artículos matriz cuadradaubicado debajo de la diagonal principal son cero, entonces se llama una matriz de este tipo matriz de triangular superior. Por ejemplo, $ \\ Izquierda (\\ Begin (Array) (CCCC) 2 y 9 y 1 \\ \\ \\ \\\\ 0 03 y 9 y 0 \\ \\\\ 0 03 y 0 y 0 y 0 \\ \\\\ 0 ° 0 y 0 y 0 y 6 \\ End (Array) \\ Derecha) $ - Matriz Triangular superior. Observe que en la definición de la matriz triangular superior, se dice nada sobre los valores de los elementos ubicados por encima de la diagonal principal o en la diagonal principal. Pueden ser cero o no, es insignificante. Por ejemplo, $ \\ IZQUIERDA (\\ COMENZA (ARRAY) (CCC) 0 y 0 y 9 \\\\ 0 y 0 \\ \\ \\ 0 y 0 \\ \\ 0 & 0 \\ \\ 0 y 0 \\ \\ 0 & 0 \\ \\ 0 & 0 \\ Fin (Array) \\ Derecha) $ También es una matriz triangular superior.
Si todos los elementos de la matriz cuadrada, ubicados sobre la diagonal principal, son cero, entonces se llama una matriz de este tipo matriz triangular inferior. Por ejemplo, $ \\ Izquierda (\\ Begin (Array) (CCCC) (CCCC) (CCCC) 3,00 y 03:3.70 \\ \\ \\ \\ \\ \\ \\ 5 y 1 1,093 0 \\ \\\\ 8 y 1 y 0 \\ \\\\ 5 y 1 y 0 y 0 y 6 \\ End (Array) \\ Derecha) $ - Matriz triangular inferior. Tenga en cuenta que al definir la matriz triangular inferior, se dice nada sobre los valores de los elementos ubicados debajo o en la diagonal principal. Pueden ser cero o no, no importa. Por ejemplo, $ \\ IZQUIERDA (\\ BEGE (Array) (CCC) -5 y 0 y 0 \\\\ 0 \\ 0 y 0 y 0 \\\\ 0 \\ 0 y 0 y 9 \\ End (Array) \\ Derecha) $ y $ \\ izquierda (\\ Comenzar (matriz) (CCC) 0,70 \\ \\ \\ \\ \\ \\ \\ 0 y 0 y 0 \\ \\ 0 y 0 y 0 \\ 0 \\ 0 y 0 \\ \\ 0 y 0 \\ 0 \\ 0 y 0 \\ \\ 0,070 \\ 0 \\ 0,070 \\ \\ 0,070 \\ 0 \\ 0,070 \\ \\ 0,070
Se llama matriz cuadrada diagonalSi todos los elementos de esta matriz que no están acostados en la diagonal principal son cero. Ejemplo: $ \\ Izquierda (\\ Begin (Array) (CCCC) (CCCC) 3 Cómo 0 y 0 y así '6 € 0 € 0 € Y 0 \u003cbr\u003e así 0 0,0 y 0,0 y 0,0 y 0 y 0 y 0 y 0 \\ 0 y 0 y 0 y 0 \\ \\ 0,09 0,09 \\ \\ \\ 0,09 0,09 \\ \\ 0,09 0 € (Array) \\ Derecha) $. Los elementos en la diagonal principal pueden ser cualquier (igual cero o no), es insignificante.
Se llama matriz diagonal ÚnicoSi todos los elementos de esta matriz ubicada en la diagonal principal son iguales a 1. Por ejemplo, $ \\ IZQUIERDA (\\ BEGE (Array) (CCCC) 1 y 0 y 0 \\\\ 0 y 1 y 0 \\\\ 0 & 0 y 1 \\ End (Array) \\ Derecha) $ es una matriz de cuarto orden; $ \\ izquierda (\\ comienzan (matriz) (CC) 1 y 0 \\\\ 0 y 1 \\ FIN (Array) \\ Derecha) $ es una matriz individual de segundo orden.
En julio de 2020, la NASA lanza una expedición a Marte. La nave espacial entregará un medio electrónico a Marte con los nombres de todos los participantes registrados de la expedición.
El registro de los participantes está abierto. Obtenga su boleto para Marte en este enlace.
Si este post decidió su problema o simplemente le gustó, comparte un enlace con mis amigos en las redes sociales.
Una de estas opciones de código debe copiarse e insertar en el código de su página web, preferiblemente entre las etiquetas
y o inmediatamente después de la etiqueta . Según la primera versión, Mathjax se carga más rápido y disminuye la página. Pero la segunda opción rastrea y carga automáticamente las últimas versiones de Mathjax. Si inserta el primer código, deberá actualizarse periódicamente. Si inserta el segundo código, las páginas se cargarán más lentamente, pero no tendrá que monitorear constantemente las actualizaciones de Mathjax.Conectar Mathjax es la forma más fácil de blogger o WordPress: agregue un widget para insertar un código JavaScript de terceros para insertar la primera o segunda versión del código de descarga que se presenta anteriormente y coloque el widget más cercano al principio de la plantilla (por cierto, , no es todo necesario, ya que el script de Mathjax está cargado de forma asíncrona). Eso es todo. Ahora lea la sintaxis de MathML, Latex y Asciimathml Markup, y está listo para insertar fórmulas matemáticas En las páginas web de su sitio.
Otra víspera de Año Nuevo ... Tiempo helado y copos de nieve en el vidrio de la ventana ... Todo esto me impulsó a escribir sobre ... Fractales y sobre lo que sabe sobre estas tungs alfa. En esta ocasión, hay un artículo interesante en el que hay ejemplos de estructuras fractales bidimensionales. Aquí consideraremos ejemplos más complejos de fractales tridimensionales.
El fractal se puede imaginar claramente (describir), como una forma geométrica o un cuerpo (teniendo en cuenta que ambos hay muchos, en este caso, un conjunto de puntos), cuyos detalles tienen la misma forma que la figura original. Es decir, es una estructura similar a sí misma, considerando los detalles de los cuales con un aumento, veremos la misma forma que sin aumentar. Mientras que en el caso de una forma geométrica convencional (no fractal), con un aumento, veremos los detalles que tienen más forma simpleque la figura original en sí. Por ejemplo, con un aumento suficientemente grande, la parte de la elipse se parece a una línea recta. Con los fractales, esto no sucede: con cualquier aumento, veremos nuevamente la misma forma compleja, que repetirá una y otra vez.
Benoit Mandelbrot (Benoit Mandelbrot), el fundador de la ciencia de los fractales, en su artículo Fractales y arte en nombre de la ciencia escribió: "Los fractales son formas geométricas que son igualmente complejas en sus detalles, como en su forma general. Es decir, Si parte del fractal se incrementará al tamaño del conjunto, se verá como un entero, o exactamente, o, posiblemente, con una pequeña deformación ".
Para llevar la matriz a un tipo escalonado (Fig. 1.4), debe realizar los siguientes pasos.
1. En la primera columna, seleccione un elemento que no sea cero ( elemento de plomo ). Una cadena con un elemento líder ( cadena principal ) Si no es el primero, reorganizar en la primera línea (conversión I tipo). Si no hay maestría en la primera columna (todos los elementos son cero), no excluimos esta columna y continuamos buscando el elemento de plomo en el resto de la matriz. La conversión termina si todas las columnas están excluidas o en la parte restante de la matriz todos los elementos cero.
2. Divida todos los elementos de la cadena de host al elemento de plomo (transformación tipo II). Si la línea principal es la última, entonces, en esta transformación debe terminarse.
3. A cada fila ubicada debajo del cable, agregue una línea líder multiplicada por un número de este tipo, respectivamente, de modo que los elementos que se encuentran debajo del cable sean iguales a cero (transformación Tipo III).
4. Al eliminar la línea y la columna de la consideración, en cuya intersección es el elemento líder, vaya a la cláusula 1, en la que todas las acciones descritas se aplican al resto de la matriz.
El teorema es sobre la fila de una fila de una fila del elemento.
El teorema de definición para los elementos de una cadena o columna le permite reducir el cálculo del determinante - ordenar () calcular los determinantes del procedimiento. .
Si el determinante tiene elementos iguales de cero, entonces el más conveniente para descomponer el determinante para los elementos de la fila o columna, que contiene el mayor número de ceros.
Usando las propiedades de los determinantes, puede convertir el determinante - el pedido para que todos los elementos de alguna fila o columna, excepto uno, se vuelvan iguales a cero. Así, el cálculo del determinante. - orden, si es diferente de cero, se reducirá al cálculo de un determinante - pedido.
Tarea 3.1.Calcular el determinante
Decisión.Agregar la primera línea primero, al tercero, la primera, multiplicada por 2, a la cuarta, la primera, multiplicada por -5, obtenemos
Descomposición del determinante para los elementos de la primera columna, tenemos
![]() .
.
En el determinante resultante de la tercera orden, nos convierte en cero todos los elementos de la primera columna, excepto el primero. Para hacer esto, la segunda línea agregará la primera, multiplicada por (-1), a la tercera, multiplicada por 5, agregará la primera, multiplicada por 8. Dado que la tercera línea se multiplicó por 5, entonces (para que el Determinante no cambiar) para multiplicarlo. Tengo
El determinante resultante se descompondrá en los elementos de la primera columna:
Teorema de Laplace (1). Teorema sobre Stranki DopName (2)
1) Identifica la determinación de los elementos de cualquier fila en su IAalgebracy.
2) El resumen de los elementos del determinante para los suplementos algebraicos de los elementos correspondientes de la otra línea es cero (el teorema de la multiplicación en los suplementos algebraicos de otras personas).
Cualquier punto en el plano bajo el sistema de coordenadas seleccionado es dado por un par (α, β) de sus coordenadas; Los números α y β también pueden entenderse como las coordenadas del vector de radio con el fin en este punto. De manera similar, en el espacio Troika (α, β, γ) determina el punto o vector con las coordenadas α, β, γ. Esto se basa en un lector conocido la interpretación geométrica de los sistemas de ecuaciones lineales con dos o tres incógnitas. Entonces, en el caso de un sistema de dos ecuaciones lineales con dos desconocidas.
un 1 x + b 1 y \u003d c 1,
a 2 X + B 2 Y \u003d C 2
cada una de las ecuaciones se interpreta tan recta en el plano (ver Fig. 26), y la solución (α, β) es como un punto de intersección de estos directos o como un vector con las coordenadas de aire (la cifra corresponde al caso cuando El sistema tiene una sola solución).
 Higo. 26.
Higo. 26.
De manera similar, puede inscribirse con el sistema de ecuaciones lineales con tres desconocidas, interpretando cada ecuación como la ecuación del plano en el espacio.
En las matemáticas y varias aplicaciones (en particular, en la teoría de la codificación), es necesario lidiar con los sistemas de ecuaciones lineales que contienen más de tres desconocidas. El sistema de ecuaciones lineales con n desconocido x 1, x 2, ..., x n se llama un conjunto de ecuaciones de la especie.
un 11 x 1 + a 12 x 2 + ... + y 1n x n \u003d b 1,
a 21 x 1 + A 22 x 2 + ... + A 2N X N \u003d B 2,
. . . . . . . . . . . . . . . . . . . . . . (1)
y m1 x 1 + y m2 x 2 + ... + y mn x n \u003d b m,
donde un IJ y B i son números válidos arbitrarios. El número de ecuaciones en el sistema puede ser cualquiera y no está asociado con el número de desconocido. Los coeficientes en desconocidos y IJ tienen una doble numeración: el primer índice que indica el número de la ecuación, el segundo índice J es el número de lo desconocido, que cuesta este coeficiente. Cualquier solución del sistema se entiende como un conjunto (válido) de los valores de desconocido (α 1, α 2, ..., α n), energizando cada ecuación en igualdad fiel.
Aunque la interpretación geométrica directa del sistema (1) en N\u003e 3 ya no es posible, pero es bastante posible y, en muchos sentidos, es conveniente extenderse a un lenguaje arbitrario N geométrico del espacio de dos o tres dimensiones. Este objetivo y sirve definiciones adicionales.
Cualquier conjunto ordenado de N números válidos (α 1, α 2, ..., α n) se denomina vector aritmético N-dimensional, y los números α 1, α 2, ..., α n coordenadas de este vector.
Para designar vectores, generalmente es audaz y para el vector A con las coordenadas α 1, α 2, ..., α n, se guarda una forma regular de grabación:
a \u003d (α 1, α 2, ..., α n).
Por analogía con un plano convencional, el conjunto de todos los vectores n-dimensionales que satisfacen la ecuación lineal con n desconocidos se denomina hiperplano en el espacio n-dimensional. Con esta definición, el conjunto de todas las soluciones del sistema (1) no es más que la intersección de varios hiperplanos.
La adición y la multiplicación de los vectores n-dimensionales están determinados por las mismas reglas que para los vectores convencionales. A saber, si
a \u003d (α 1, α 2, ..., α n), b \u003d (β 1, β 2, ..., β n) (2)
Dos vector n-dimensional, luego su suma se llama vector.
α + β \u003d (α 1 + β 1, α 2 + β 2, ..., α n + β n). (3)
El producto del vector y el número λ se llama vector.
λа \u003d (λα 1, λα 2, ..., λα n). (cuatro)
El conjunto de todos los vectores aritméticos n-dimensionales con las operaciones de la adición de vectores y la multiplicación del vector se llama un espacio vectorial n-dimensional aritmético l n.
Usando las operaciones ingresadas, es posible considerar combinaciones lineales arbitrarias de varios vectores, es decir, la expresión
λ 1 A 1 + λ 2 A 2 + ... + λ k a k,
donde λ i es un número válido. Por ejemplo, una combinación lineal de vectores (2) con coeficientes λ y μ es un vector
λа + μB \u003d (λα 1 + μβ 1, λα 2 + μβ 2, ..., λα n + μβ n).
En el espacio tridimensional de los vectores, la parte superior de los vectores I, J, k (Ortops de coordenadas) desempeñan un papel especial, que se descompone por cualquier vector A:
a \u003d xi + yj + zk,
donde X, Y, Z son números válidos (las coordenadas del vector A).
En caso n-dimensional, los siguientes vectores desempeñan el mismo papel:
e 1 \u003d (1, 0, 0, ..., 0),
e 2 \u003d (0, 1, 0, ..., 0),
e 3 \u003d (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
e n \u003d (0, 0, 0, ..., 1).
Cada vector A es, obviamente, una combinación lineal de vectores E 1, E 2, ..., E n:
a \u003d A 1 E 1 + A 2 E 2 + ... + A N E N, (6)
además, los coeficientes α 1, α 2, ..., α n coinciden con las coordenadas del vector a.
Denote por 0 Vector, todas las coordenadas de las cuales son cero (brevemente, cero vector), introducimos la siguiente definición importante:
El sistema de vectores A 1, y 2, ... y K se llama lineal dependiente, si hay una combinación lineal de vector igual.
λ 1 A 1 + λ 2 A 2 + ... + λ k a k \u003d 0,
en el que al menos uno de los coeficientes H 1, λ 2, ..., λ k es diferente de cero. De lo contrario, el sistema se llama linealmente independiente.
Entonces, vectores
a 1 \u003d (1, 0, 1, 1), A 2 \u003d (1, 2, 1, 1), y 3 \u003d (2, 2, 2, 2)
depende linealmente porque
a 1 + A 2 - A 3 \u003d 0.
La dependencia lineal, como se puede ver en la definición, es equivalente (en K ≥ 2) al hecho de que al menos uno de los vectores del sistema es una combinación lineal de los restantes.
Si el sistema consta de dos vectores a 1, A 2, entonces la dependencia lineal del sistema significa que uno de los vectores es proporcional a otro, por ejemplo, y 1 \u003d λa 2; En un caso tridimensional, es equivalente a la colinealidad de los vectores A 1 y A 2. De manera similar, la dependencia lineal del sistema I de tres vectores en el espacio convencional significa la compatación de estos vectores. El concepto de dependencia lineal es, por lo tanto, la generalización natural de los conceptos de colinealidad y acompañamiento.
Es fácil asegurarse de que los vectores E 1, E 2, ..., E n del sistema (5) son linealmente independientes. Por lo tanto, hay sistemas de los vectores linealmente independientes en el espacio n-dimensional. Se puede demostrar que cualquier sistema de mayor número de vectores depende linealmente.
Cualquier sistema A 1, A 2, ... y N de n vectores independientes linealmente independientes del espacio n-dimensional L n se llama su base.
Cualquier vector y los espacios l n se despliega, y además, por el vector de una base arbitraria a 1, y 2, ..., y N:
a \u003d λ 1 A 1 + λ 2 A 2 + ... + λ n A n.
Este hecho se establece fácilmente en función de la definición de la base.
Continuando una analogía con un espacio tridimensional, es posible en el caso n-dimensional determinar el producto escalar A · B de vectores, creyendo
a · b \u003d α 1 β 1 + α 2 β 2 + ... + α n β n.
Con esta definición, se conservan todas las propiedades básicas del producto escalar de los vectores tridimensionales. Los vectores A y B se llaman ortogonal si su producto escalar es cero:
α 1 β 1 + α 2 β 2 + ... + α n β n \u003d 0.
En la teoría de los códigos lineales, se usa otro concepto importante: el concepto de subespacio. El subconjunto del espacio V L N se llama subespacio de este espacio si
1) Para cualquier vectores A, B, pertenecientes a V, su suma A + B también pertenece a V;
2) Para cualquier vector A, perteneciente a V, y para cualquier número real λ, el vector λa también pertenece a V.
Por ejemplo, el conjunto de todas las combinaciones lineales de vectores E 1, E 2 del sistema (5) será un subespacio del espacio l n.
En un álgebra lineal, se demuestra que en cada subespacio V, hay un sistema de vectores tan linealmente independiente A 1, A 2, ..., un k, que cada vector y subespacio es una combinación lineal de estos vectores:
a \u003d λ 1 A 1 + λ 2 A 2 + ... + λ k a k.
El sistema de vectores especificado se llama la base del subespacio V.
Desde la definición del espacio y el subespacio sigue inmediatamente que el espacio L N es el grupo conmutativo en relación con la formación de vectores, y cualquiera de sus subespacio V es un subgrupo de este grupo. En este sentido, es posible, por ejemplo, considerar las clases adyacentes del espacio L N por subespacimiento V.
En conclusión, enfatizamos que si en la teoría del espacio aritmético n-dimensional en lugar de números válidos (es decir, los elementos del campo de los números válidos) consideran los elementos de un campo arbitrario F, luego todas las definiciones y los hechos dados anteriormente. habría conservado fuerza.
En la teoría de la codificación, un rol importante desempeña el caso cuando el campo F campo de deducción Z P, que, como sabemos, por supuesto. En este caso, el espacio n-dimensional correspondiente también contiene, ya que no es difícil ver, los elementos P N.
El concepto de espacio, así como el concepto de un grupo y anillos, también permite una definición axiomática. Para obtener más información, enviamos al alimentador a cualquier curso de un álgebra lineal.
Lynіin Kombіnatsiya. Vector del sistema Inepless Lynіino Zarezhnі Tu.
instyer combinación de vectores.
Combinación lineal de vectores. ![]() llamar vector
llamar vector
dónde ![]() - Coeficientes de combinación lineales. Si un
- Coeficientes de combinación lineales. Si un ![]() la combinación se llama trivial, si no es trivial.
la combinación se llama trivial, si no es trivial.
Dependencia lineal e independencia de los vectores.
Sistema ![]() dependiente linealmente
dependiente linealmente 
Sistema ![]() independiente linealmente
independiente linealmente 
Criterio de dependencia lineal de los vectores.
Para vectores ![]() (r\u003e 1.) Fue dependiente linealmente, es necesario y suficiente para que al menos uno de estos vectores sea una combinación lineal del resto.
(r\u003e 1.) Fue dependiente linealmente, es necesario y suficiente para que al menos uno de estos vectores sea una combinación lineal del resto.
La dimensión del espacio lineal.
Espacio lineal V.llamada nORTE.- dimensional (tiene dimensión nORTE.), si en él:
1) existe nORTE.vectores independientes lineales;
2) cualquier sistema n + 1.los vectores son linealmente dependientes.
Designaciones: nORTE.\u003d tenue V.;.
Se llama el sistema de vectores. dependiente linealmentesi existe nenulevaconjunto con una combinación lineal.
Se llama el sistema de vectores. independiente linealmentesi de la combinación lineal de igualdad cero.
debe ser igual a cero todascoeficientes
La cuestión de la dependencia lineal de los vectores en el caso general se reduce a la cuestión de la existencia de una solución no cero en un sistema homogéneo de ecuaciones lineales con coeficientes igual a las coordenadas relevantes de estos vectores.
Para asignar bien el concepto de "dependencia lineal", el sistema de vectores "independencia lineal", es útil resolver las tareas del siguiente tipo:
Lynіin zarezhnіst.і іі іі іі en critia enlóneamente.
Vectores del sistema es dependiente linealmente, y solo si uno de los vectores del sistema es una combinación lineal de los vectores restantes de este sistema.
Evidencia. Deje que el sistema de los vectores dependa linealmente de los vectores. Luego hay un conjunto de coeficientes. ![]() que, con al menos un coeficiente difieren de cero. Vamos a fingir que. Luego
que, con al menos un coeficiente difieren de cero. Vamos a fingir que. Luego
es decir, es una combinación lineal de los vectores restantes del sistema.
Deje que uno de los vectores del sistema sea una combinación lineal de los vectores restantes. Supongamos que esto es un vector, eso es ![]() . Es obvio que . Se obtuvo que la combinación lineal de vectores del sistema es cero, y uno de los coeficientes difiere de cero (igual).
. Es obvio que . Se obtuvo que la combinación lineal de vectores del sistema es cero, y uno de los coeficientes difiere de cero (igual).
Oración10 . 7 Si el sistema de vectores comprende un subsistema linealmente dependiente, entonces todo el sistema depende linealmente.
Evidencia.
Dejar en el sistema de los vectores del subsistema. ![]() , es dependiente linealmente, es decir, y al menos un coeficiente es diferente de cero. Luego haz una combinación lineal. Obviamente, esta combinación lineal es cero, y que no hay ningún cero entre los coeficientes.
, es dependiente linealmente, es decir, y al menos un coeficiente es diferente de cero. Luego haz una combinación lineal. Obviamente, esta combinación lineal es cero, y que no hay ningún cero entre los coeficientes.
El sistema base de vector_v, їїsts a las autoridades.
La base del sistema distintivo de vectores no se llama equivalente al subsistema linealmente independiente. El sistema cero de la base no tiene.
Propiedad 1:La base del sistema independiente lineal coincide con ella misma.
Ejemplo: El sistema de vectores lineales independientes, ya que ninguno de los vectores puede exhalar linealmente a través del resto.
Propiedad 2: (Base de criterios)El subsistema lineal independiente de este sistema es su base si y solo si es más linealmente independiente.
Evidencia:Sistema Dana Necesidad Deja la base. Luego, por definición y, si, dónde, el sistema es linealmente dependiente, ya que tal vez es linealmente a través de, por lo tanto, la más linealmente independiente. AdecuaciónDeje el subsistema más linealmente independiente, entonces dónde. Ejercicios linealmente dependientes linealmente a través de la base del sistema.
Propiedad 3: (Propiedad Básica Básica)Cada vector del sistema se administra a través de la base de datos individualmente.
EvidenciaDeje que el vector se realice a través de la base de datos de dos maneras, entonces:, entonces
Vector del sistema de rango.
|
Definición:El rango del sistema distinto de vectores lineales se llama el número de vectores de su base. El rango del sistema cero por definición es cero. Propiedades de rango:1) El rango del sistema linealmente independiente coincide con el número de sus vectores. 2) El rango del sistema dependiente linealmente es menor que el número de sus vectores. 3) Los rangos de sistemas equivalentes coinciden -RankRank. 4) El rango bajo el sistema es menor o igual al sistema de rango. 5) Si Rainank, entonces la base total. 6) El rango del sistema no cambia si se le agrega el vector, que es una combinación lineal de los vectores restantes del sistema. 7) El rango del sistema no cambia si el vector se elimina de él, que es una combinación lineal de otros vectores. |
Para encontrar el sistema de vectores de rango, debe usar el método Gaussai para llevar el sistema a forma triangular o trapezoidal.
Ekwіvalent_ Vector del sistema.
Ejemplo:
Transformamos los datos del vector en la matriz para encontrar la base. Obtenemos: 
Ahora con la ayuda del método GAUSS, convertiremos una matriz a la forma trapezoidal:
1) En nuestra matriz principal, nutriremos la primera primera columna, además de la primera línea desde la segunda, la primera multiplicada, desde la tercera, la primera multiplicada, y no tomaremos nada del cuarto. , Dado que el primer elemento de la cuarta línea, es decir, la intersección de la primera columna y la cuarta línea es cero. Obtenemos una matriz:  2) Ahora, en la matriz, cambie las líneas 2, 3 y 4 a la simplicidad de la solución, que estaría en el sitio del elemento. Cambiaré la cuarta línea para poner en lugar del segundo, el segundo en lugar del tercero y tercero al cuarto lugar. Obtenemos una matriz:
2) Ahora, en la matriz, cambie las líneas 2, 3 y 4 a la simplicidad de la solución, que estaría en el sitio del elemento. Cambiaré la cuarta línea para poner en lugar del segundo, el segundo en lugar del tercero y tercero al cuarto lugar. Obtenemos una matriz:  3) En la matriz, anulas todos los elementos bajo el elemento. Dado que nuevamente, el elemento de nuestra MATRE es cero es cero, no estamos tomando nada de la cuarta línea, y agregue el tercero al tercero multiplicado por. Obtenemos una matriz:
3) En la matriz, anulas todos los elementos bajo el elemento. Dado que nuevamente, el elemento de nuestra MATRE es cero es cero, no estamos tomando nada de la cuarta línea, y agregue el tercero al tercero multiplicado por. Obtenemos una matriz:  4) Volvemos a cambiar nuevamente en la matriz de la cadena 3 y 4 lugares. Obtenemos una matriz:
4) Volvemos a cambiar nuevamente en la matriz de la cadena 3 y 4 lugares. Obtenemos una matriz:  5) En el matriarpetrybavim, la tercera línea, multiplicada por 5. Obtenemos una matriz que tendrá un aspecto triangular:
5) En el matriarpetrybavim, la tercera línea, multiplicada por 5. Obtenemos una matriz que tendrá un aspecto triangular: 
Sistemas, sus rangos coinciden debido a las propiedades de clasificación y su rango es rango de rango
Observaciones:1) A diferencia del método Gauss tradicional, si todos los elementos se dividen en un cierto número en la cadena de matriz, no tenemos el derecho de reducir la cadena de la matriz en virtud de las propiedades de la matriz. Si queremos reducir la cadena a un cierto número, tendrá que cortar la matriz completa a este número. 2) En el caso de que obtengan una cadena dependiente lineal, podemos eliminarla de nuestra matriz y reemplazar a cero cadena. Ejemplo:
 Se ve inmediatamente que la segunda línea se expresa a través de la primera, si la primera es la primera en 2. En el caso THIAK, podemos reemplazar toda la segunda cadena a cero. Obtenemos:
Se ve inmediatamente que la segunda línea se expresa a través de la primera, si la primera es la primera en 2. En el caso THIAK, podemos reemplazar toda la segunda cadena a cero. Obtenemos:  Como resultado, llevar una matriz o a un triangular, o a una forma trapezoidal, donde no tiene vectores dependientes linealmente, todos los vectores cero de la matriz y serán la base de la matriz, pero su número de rango.
Como resultado, llevar una matriz o a un triangular, o a una forma trapezoidal, donde no tiene vectores dependientes linealmente, todos los vectores cero de la matriz y serán la base de la matriz, pero su número de rango.
Este es también un ejemplo de un sistema de vectores en forma de gráfica: se da un sistema donde, y. La base de este sistema obviamente será un vector y, dado que los vectores se expresan a través de ellos. Este sistema en forma gráfica verá:
Elehentarnі Shuttering. Sistemas de la forma tigueosa.
Matriz de conversión elemental - Estas son tales conversiones de la matriz, como resultado de lo cual persiste la equivalencia de matrices. Por lo tanto, las transformaciones elementales no cambian las soluciones establecidas de un sistema de ecuaciones algebraicas lineales, que representa esta matriz.
Las transformaciones elementales se utilizan en el método Gauss para llevar la matriz a forma triangular o escalonada.
Transformaciones de fila elemental Llamada:
En algunos cursos de la álgebra lineal, las cadenas de matriz no se liberan en una conversión elemental separada debido al hecho de que la permutación de dos líneas de la matriz se puede obtener utilizando la multiplicación de cualquier cadena de la matriz a la constante, y La adición de una línea diferente se multiplica por una constante a cualquier cadena de la matriz.
De manera similar se determinan transformaciones de columna elemental.
Transformaciones elementales reversible.
La designación indica que la matriz se puede obtener de las transformaciones elementales (o viceversa).
Definición
Se llama matriz cuadrada diagonalSi todos sus elementos de pie fuera de la diagonal principal son cero.
Comentario. Los elementos diagonales de la matriz (es decir, los elementos de pie en la diagonal principal) también pueden ser cero.
Ejemplo

Definición
Escalar Se llama una matriz diagonal, en la que todos los elementos diagonales son iguales entre sí.
Comentario. Si la matriz cero es cuadrada, entonces también es escalar.
Ejemplo
![]()
Definición
Matriz individual Se llama una matriz escalar de orden, los elementos diagonales de los cuales son iguales a 1.
Comentario. Para reducir la grabación, el orden de una sola matriz no se puede escribir, luego se indica una sola matriz.
Ejemplo
![]() - Matriz de un solo segundo orden.
- Matriz de un solo segundo orden.
2.10. Cortar la matriz a diagonal.
Matriz normal (en particular simétrica) UNA. Se puede llevar al tipo diagonal por la conversión de similitud -
UNA. = Tλt. −1
Aquí Λ \u003d DIAG (λ 1, ..., λ NORTE.) es una matriz diagonal, cuyos elementos son los valores propios de la matriz UNA., pero T. - Esta es una matriz formada por los ejes de matriz correspondientes. UNA.. T. = (v. 1 ,...,v. NORTE.).
Por ejemplo,

Higo. 23 Traying a la forma diagonal.
Matriz paso
Definición
Velocidad Llamado una matriz que cumple las siguientes condiciones:
Definición
Velocidad Se llama una matriz que contiene cadenas y en la que los primeros elementos diagonales son distintos, y los elementos subyacentes a la diagonal principal y los elementos de las últimas filas son cero, es decir, esta es una matriz de la forma:

Definición
El elemento principal Una cierta fila de la matriz se llama su primer elemento distinto de cero.
Ejemplo
La tarea. Encuentra los elementos principales de cada fila de la matriz. ![]()
Decisión. El elemento principal de la primera línea es el primer elemento distinto de cero de esta línea, y por lo tanto, el elemento principal de la cadena en el número 1; De manera similar, el elemento principal de la segunda línea.
Otra definición de una matriz escalonada.
Definición
La matriz se llama velocidad, si A:
todas sus líneas cero están de pie tras nozero;
en cada línea distintiva, a partir de la segunda, su elemento principal está a la derecha (en una columna con un número grande) del elemento principal de la línea anterior.
Por definición a las matrices de paso, atraeremos una matriz cero, así como una matriz que contiene una línea.
Ejemplo
Ejemplos de matrices escalonadas:
![]() , ,
, ,  ,
,  ,
,
Ejemplos de matrices que no están a paso:
![]() ,
,  ,
, 
Ejemplo
La tarea. Averigüe si la matriz es  paso.
paso.
Decisión. Verifique el cumplimiento de las condiciones de la definición:
Por lo tanto, la matriz especificada es un paso.
 Aspecto de error durante el lanzamiento del programa
Aspecto de error durante el lanzamiento del programa Fragation Plugin para Firefox
Fragation Plugin para Firefox Cómo mostrar carpetas y archivos ocultos en Windows
Cómo mostrar carpetas y archivos ocultos en Windows Maneras Cómo hacer una pantalla en una computadora portátil más brillante o más oscura
Maneras Cómo hacer una pantalla en una computadora portátil más brillante o más oscura Cómo formatear una unidad flash, protección contra el disco
Cómo formatear una unidad flash, protección contra el disco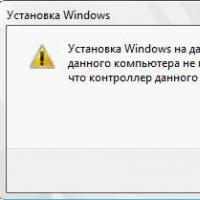 Si la instalación de Windows a este disco no es posible
Si la instalación de Windows a este disco no es posible Durante la instalación de Windows "Asegúrese de que el controlador de este disco esté incluido en el menú BIOS de la computadora.
Durante la instalación de Windows "Asegúrese de que el controlador de este disco esté incluido en el menú BIOS de la computadora.