En Internet, incluido Habré, puede encontrar mucha información sobre el filtro Kalman. Pero es difícil encontrar una derivación fácilmente digerible de las fórmulas mismas. Sin una conclusión, toda esta ciencia se percibe como una especie de chamanismo, las fórmulas parecen un conjunto de símbolos sin rostro y, lo que es más importante, muchas declaraciones simples que se encuentran en la superficie de la teoría están más allá de la comprensión. El propósito de este artículo será hablar sobre este filtro en el lenguaje más accesible.
El filtro de Kalman es una poderosa herramienta de filtrado de datos. Su principio fundamental es que al filtrar se utiliza información sobre la física del propio fenómeno. Digamos que si está filtrando datos del velocímetro de un automóvil, entonces la inercia del automóvil le da derecho a percibir los saltos de velocidad demasiado rápidos como un error de medición. El filtro de Kalman es interesante porque, en cierto sentido, es el mejor filtro. Discutiremos con más detalle a continuación qué significan exactamente las palabras "lo mejor". Al final del artículo mostraré que en muchos casos las fórmulas se pueden simplificar hasta tal punto que casi no queda nada de ellas.

Likbez

Antes de familiarizarme con el filtro de Kalman, propongo recordar algunas definiciones y hechos simples de la teoría de la probabilidad.

Valor aleatorio

Cuando dicen que se da una variable aleatoria, quieren decir que esta variable puede tomar valores aleatorios. Toma diferentes valores con diferentes probabilidades. Cuando lanzas, digamos, un dado, caerá un conjunto discreto de valores: . Cuando se trata, por ejemplo, de la velocidad de una partícula errante, entonces, obviamente, uno tiene que lidiar con un conjunto continuo de valores. Los valores "abandonados" de una variable aleatoria se denotarán por , pero a veces usaremos la misma letra que denota una variable aleatoria: .
En el caso de un conjunto continuo de valores, la variable aleatoria se caracteriza por la densidad de probabilidad , que nos dicta que la probabilidad de que la variable aleatoria "caiga" en una pequeña vecindad de un punto de longitud es igual a . Como podemos ver en la imagen, esta probabilidad es igual al área del rectángulo sombreado debajo del gráfico:

Muy a menudo en la vida, las variables aleatorias se distribuyen según Gauss, cuando la densidad de probabilidad es .

Vemos que la función tiene forma de campana centrada en un punto y con un ancho característico del orden de .
Como estamos hablando de la distribución gaussiana, sería un pecado no mencionar de dónde vino. Así como los números están firmemente establecidos en las matemáticas y aparecen en los lugares más inesperados, la distribución gaussiana se ha arraigado profundamente en la teoría de la probabilidad. Una declaración notable que explica parcialmente la omnipresencia gaussiana es la siguiente:
Sea una variable aleatoria que tenga una distribución arbitraria (de hecho, existen algunas restricciones a esta arbitrariedad, pero no son del todo rígidas). Realicemos experimentos y calculemos la suma de los valores "abandonados" de una variable aleatoria. Hagamos muchos de estos experimentos. Está claro que cada vez recibiremos un valor diferente de la suma. En otras palabras, esta suma es en sí misma una variable aleatoria con su propia ley de distribución determinada. Resulta que para suficientemente grande, la ley de distribución de esta suma tiende a la distribución Gaussiana (por cierto, el ancho característico de la “campana” crece como ). Lea más en wikipedia: teorema del límite central. En la vida, muy a menudo hay cantidades que se componen de un gran número de variables aleatorias independientes igualmente distribuidas y, por lo tanto, se distribuyen de acuerdo con Gauss.

Significar

El valor promedio de una variable aleatoria es lo que obtenemos en el límite si realizamos muchos experimentos y calculamos la media aritmética de los valores arrojados. El valor promedio se denota de diferentes maneras: a los matemáticos les gusta denotar por (expectativa), ya los matemáticos extranjeros por (expectativa). Física misma a través de o. Designaremos en forma extranjera:.
Por ejemplo, para una distribución gaussiana, la media es .

Dispersión

En el caso de la distribución gaussiana, podemos ver claramente que la variable aleatoria prefiere caer en alguna vecindad de su valor medio. Como se puede ver en el gráfico, la dispersión característica de los valores de orden es . ¿Cómo podemos estimar esta dispersión de valores para una variable aleatoria arbitraria si conocemos su distribución? Puede dibujar un gráfico de su densidad de probabilidad y estimar el ancho característico a simple vista. Pero preferimos ir por el camino algebraico. Puede encontrar la longitud promedio de la desviación (módulo) del valor promedio: . Este valor será una buena estimación de la dispersión característica de los valores. Pero usted y yo sabemos muy bien que usar módulos en fórmulas es un dolor de cabeza, por lo que esta fórmula rara vez se usa para estimar la distribución característica.
Una forma más fácil (simple en términos de cálculos) es encontrar . Esta cantidad se llama varianza y a menudo se la conoce como . La raíz de la varianza se llama desviación estándar. La desviación estándar es una buena estimación de la dispersión de una variable aleatoria.
Por ejemplo, para una distribución gaussiana, podemos suponer que la varianza definida anteriormente es exactamente igual a , lo que significa que la desviación estándar es igual a , lo que concuerda muy bien con nuestra intuición geométrica.
De hecho, hay una pequeña estafa escondida aquí. El hecho es que en la definición de la distribución gaussiana, debajo del exponente está la expresión . Este dos en el denominador es precisamente para que la desviación estándar sea igual al coeficiente. Es decir, la fórmula de distribución gaussiana en sí misma está escrita en una forma especialmente definida por el hecho de que consideraremos su desviación estándar.

Variables aleatorias independientes

Las variables aleatorias pueden o no ser dependientes. Imagina que lanzas una aguja a un avión y anotas las coordenadas de ambos extremos de la misma. Estas dos coordenadas son dependientes, están conectadas por la condición de que la distancia entre ellas sea siempre igual a la longitud de la aguja, aunque son variables aleatorias.
Las variables aleatorias son independientes si el resultado de la primera es completamente independiente del resultado de la segunda. Si las variables aleatorias y son independientes, entonces el valor medio de su producto es igual al producto de sus valores medios:

Prueba

Por ejemplo, tener ojos azules y terminar la escuela con medalla de oro son variables aleatorias independientes. Si de ojos azules, digamos un medallista de oro , entonces medallista de ojos azules Este ejemplo nos dice que si las variables aleatorias y están dadas por sus densidades de probabilidad y , entonces la independencia de estas cantidades se expresa en el hecho de que la densidad de probabilidad (la primera valor eliminado, y el segundo) se encuentra mediante la fórmula:

Inmediatamente se sigue de esto que:

Como puedes ver, la prueba se realiza para variables aleatorias que tienen un espectro continuo de valores y están dadas por su densidad de probabilidad. En otros casos, la idea de la prueba es similar.

filtro Kalman

Formulación del problema

Denotar por el valor que vamos a medir y luego filtrar. Puede ser coordenada, velocidad, aceleración, humedad, grado de olor, temperatura, presión, etc.
Empecemos con un ejemplo sencillo, que nos llevará a la formulación de un problema general. Imagina que tenemos un coche controlado por radio que solo puede ir hacia adelante y hacia atrás. Nosotros, conociendo el peso del automóvil, la forma, la superficie de la carretera, etc., calculamos cómo el joystick de control afecta la velocidad de movimiento.

Entonces la coordenada de la máquina cambiará según la ley:

En la vida real, no podemos tener en cuenta en nuestros cálculos las pequeñas perturbaciones que actúan sobre el coche (viento, baches, piedras en la carretera), por lo que la velocidad real del coche diferirá de la calculada. Se agrega una variable aleatoria al lado derecho de la ecuación escrita:

Tenemos un sensor GPS instalado en el coche, que trata de medir la verdadera coordenada del coche y, por supuesto, no puede medirla exactamente, pero la mide con un error, que también es una variable aleatoria. Como resultado, obtenemos datos erróneos del sensor:

El problema es que, sabiendo las lecturas incorrectas del sensor, encuentre una buena aproximación para la verdadera coordenada de la máquina.
En la formulación del problema general, cualquier cosa puede ser responsable de la coordenada (temperatura, humedad...), y denotaremos el término responsable de controlar el sistema desde el exterior como (en el ejemplo con la máquina). Las ecuaciones para las lecturas de coordenadas y sensores se verán así:

Analicemos en detalle lo que sabemos:

Es útil tener en cuenta que la tarea de filtrado no es una tarea de suavizado. No pretendemos suavizar los datos del sensor, nuestro objetivo es obtener el valor más cercano a la coordenada real.

Algoritmo de Kalman

Razonaremos por inducción. Imagine que en el -ésimo paso ya hemos encontrado el valor filtrado del sensor, que se aproxima bien a la verdadera coordenada del sistema. No olvides que conocemos la ecuación que controla el cambio en una coordenada desconocida:

por lo tanto, sin obtener el valor del sensor todavía, podemos suponer que en el paso el sistema evoluciona de acuerdo con esta ley y el sensor mostrará algo cercano a . Desafortunadamente, no podemos decir nada más preciso todavía. Por otro lado, en el paso tendremos una lectura inexacta del sensor en nuestras manos.
La idea de Kalman es la siguiente. Para obtener la mejor aproximación a la coordenada real, debemos elegir un término medio entre la lectura inexacta del sensor y nuestra predicción de lo que esperábamos ver. Le daremos un peso a la lectura del sensor y el valor predicho tendrá un peso:

El coeficiente se llama coeficiente de Kalman. Depende del paso de la iteración, por lo que sería más correcto escribir , pero por ahora, para no saturar las fórmulas de cálculo, omitiremos su índice.
Debemos elegir el coeficiente de Kalman de tal manera que el valor óptimo resultante de la coordenada sea el más cercano al valor verdadero. Por ejemplo, si sabemos que nuestro sensor es muy preciso, confiaremos más en su lectura y le daremos más peso al valor (cerca de uno). Si el sensor, por el contrario, no es del todo preciso, entonces nos centraremos más en el valor predicho teóricamente de .
En general, para encontrar el valor exacto del coeficiente de Kalman, simplemente se necesita minimizar el error:

Usamos las ecuaciones (1) (las del recuadro azul) para reescribir la expresión del error:

Prueba

Ahora es el momento de discutir qué significa la expresión minimizar el error. Después de todo, el error, como vemos, es en sí mismo una variable aleatoria y cada vez toma valores diferentes. Realmente no existe un enfoque único para todos para definir lo que significa que el error sea mínimo. Al igual que en el caso de la varianza de una variable aleatoria, cuando tratamos de estimar el ancho característico de su dispersión, aquí elegiremos el criterio más simple para los cálculos. Minimizaremos la media del error cuadrático:

Escribamos la última expresión:

Prueba

Del hecho de que todas las variables aleatorias incluidas en la expresión para son independientes, se deduce que todos los términos "cruzados" son iguales a cero:

Usamos el hecho de que , entonces la fórmula para la varianza parece mucho más simple: .

Esta expresión toma un valor mínimo cuando (igual la derivada a cero):

Aquí ya estamos escribiendo una expresión para el coeficiente de Kalman con índice de paso, por lo que enfatizamos que depende del paso de iteración.
Sustituimos el valor óptimo obtenido en la expresión para la que hemos minimizado. Nosotros recibimos;

Nuestra tarea está resuelta. Hemos obtenido una fórmula iterativa para calcular el coeficiente de Kalman.
Resumamos nuestros conocimientos adquiridos en un cuadro:

Ejemplo

codigo matlab

limpiar todo; N=100% número de muestras a=0,1% aceleración sigmaPsi=1 sigmaEta=50; k=1:N x=k x(1)=0 z(1)=x(1)+normrnd(0,sigmaEta); para t=1:(N-1) x(t+1)=x(t)+a*t+normrnd(0,sigmaPsi); z(t+1)=x(t+1)+normrnd(0,sigmaEta); fin; %filtro kalman xOpt(1)=z(1); eOpt(1)=sigmaEta; para t=1:(N-1) eOpt(t+1)=raíz cuadrada((sigmaEta^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEta^2+eOpt(t)^2+ sigmaPsi^2)) K(t+1)=(eOpt(t+1))^2/sigmaEta^2 xOpt(t+1)=(xOpt(t)+a*t)*(1-K(t +1))+K(t+1)*z(t+1) fin; plot(k,xopt,k,z,k,x)

Análisis

Si rastreamos cómo cambia el coeficiente de Kalman con el paso de iteración, podemos mostrar que siempre se estabiliza en un valor determinado. Por ejemplo, cuando los errores RMS del sensor y el modelo se relacionan entre sí como diez a uno, entonces la gráfica del coeficiente de Kalman dependiendo del paso de iteración se ve así:

En el siguiente ejemplo, discutiremos cómo esto puede hacer nuestras vidas mucho más fáciles.

Segundo ejemplo

En la práctica, suele ocurrir que no sabemos nada sobre el modelo físico de lo que estamos filtrando. Por ejemplo, desea filtrar las lecturas de su acelerómetro favorito. No sabes de antemano por qué ley pretendes girar el acelerómetro. La mayor parte de la información que puede obtener es la variación del error del sensor. En una situación tan difícil, toda la ignorancia del modelo de movimiento puede convertirse en una variable aleatoria:

Pero, francamente, tal sistema ya no satisface las condiciones que impusimos a la variable aleatoria, porque ahora toda la física del movimiento desconocida para nosotros está oculta allí, y por lo tanto no podemos decir que en diferentes momentos, los errores de la modelo son independientes entre sí y que sus valores medios son cero. En este caso, en general, la teoría del filtro de Kalman no es aplicable. Pero, no vamos a prestar atención a este hecho, sino, estúpidamente aplicar todo el coloso de fórmulas, eligiendo los coeficientes ya ojo, para que los datos filtrados se vean bonitos.
Pero hay otra manera mucho más fácil de hacerlo. Como vimos anteriormente, el coeficiente de Kalman siempre se estabiliza en el valor . Por lo tanto, en lugar de seleccionar los coeficientes y encontrar el coeficiente de Kalman usando fórmulas complejas, podemos considerar que este coeficiente es siempre una constante y seleccionar solo esta constante. Esta suposición estropeará casi nada. En primer lugar, ya estamos utilizando ilegalmente la teoría de Kalman y, en segundo lugar, el coeficiente de Kalman se estabiliza rápidamente en una constante. Al final, todo será muy simple. No necesitamos ninguna fórmula de la teoría de Kalman, solo necesitamos elegir un valor aceptable e insertarlo en la fórmula iterativa:

El siguiente gráfico muestra datos de un sensor ficticio filtrados de dos maneras diferentes. Siempre que no sepamos nada sobre la física del fenómeno. La primera forma es honesta, con todas las fórmulas de la teoría de Kalman. Y el segundo está simplificado, sin fórmulas.

Como podemos ver, los métodos son casi los mismos. Se observa una pequeña diferencia solo al principio, cuando el coeficiente de Kalman aún no se ha estabilizado.

Discusión

Como hemos visto, la idea principal del filtro de Kalman es encontrar un coeficiente tal que el valor filtrado

en promedio diferiría menos que nada del valor real de la coordenada. Vemos que el valor filtrado es una función lineal de la lectura del sensor y el valor filtrado anterior. Y el valor filtrado anterior es, a su vez, una función lineal de la lectura del sensor y el valor filtrado anterior. Y así sucesivamente, hasta que la cadena esté completamente desplegada. Es decir, el valor filtrado depende de todo lecturas anteriores del sensor linealmente:

Por lo tanto, el filtro de Kalman se llama filtro lineal.
Se puede demostrar que el filtro de Kalman es el mejor de todos los filtros lineales. Lo mejor en el sentido de que el cuadrado medio del error del filtro es mínimo.

Caso multivariante

Toda la teoría del filtro de Kalman se puede generalizar al caso multidimensional. Las fórmulas allí parecen un poco más aterradoras, pero la idea misma de su derivación es la misma que en el caso unidimensional. Puedes verlos en este excelente artículo: http://habrahabr.ru/post/140274/ .
Y en este maravilloso video un ejemplo de cómo usarlos.

Los filtros Wiener son los más adecuados para procesos de procesamiento o segmentos de procesos como un todo (procesamiento de bloques). El procesamiento secuencial requiere una estimación actual de la señal en cada ciclo, teniendo en cuenta la información recibida en la entrada del filtro durante el proceso de observación.

Con el filtrado de Wiener, cada nueva muestra de señal requeriría volver a calcular todos los pesos de filtro. En la actualidad son muy utilizados los filtros adaptativos, en los que se utiliza nueva información entrante para corregir continuamente la estimación de señal realizada previamente (seguimiento de objetivos en radar, sistemas de control automático en control, etc.). De particular interés son los filtros adaptativos del tipo recursivo, conocidos como filtro de Kalman.

Estos filtros son ampliamente utilizados en lazos de control en sistemas automáticos de regulación y control. De ahí es de donde procedían, como lo demuestra la terminología tan específica utilizada para describir su trabajo como el espacio de estado.

Una de las principales tareas que deben resolverse en la práctica de la computación neuronal es obtener algoritmos de aprendizaje de redes neuronales rápidos y confiables. En este sentido, puede ser útil utilizar un algoritmo de aprendizaje de filtros lineales en el bucle de realimentación. Dado que los algoritmos de aprendizaje son de naturaleza iterativa, dicho filtro debe ser un estimador recursivo secuencial.

Problema de estimación de parámetros

Uno de los problemas de la teoría de las soluciones estadísticas, que tiene una gran importancia práctica, es el problema de la estimación de los vectores de estado y parámetros de los sistemas, que se formula de la siguiente manera. Supongamos que es necesario estimar el valor del parámetro vectorial $X$, que es inaccesible a la medición directa. En su lugar, se mide otro parámetro $Z$, dependiendo de $X$. La tarea de estimación es responder a la pregunta: ¿qué se puede decir acerca de $X$ dados $Z$? En el caso general, el procedimiento para la estimación óptima del vector $X$ depende del criterio de calidad aceptado para la estimación.

Por ejemplo, el enfoque bayesiano del problema de estimación de parámetros requiere información completa a priori sobre las propiedades probabilísticas del parámetro estimado, lo que a menudo es imposible. En estos casos se recurre al método de mínimos cuadrados (LSM), que requiere mucha menos información a priori.

Consideremos la aplicación de LSM para el caso en que el vector de observación $Z$ está conectado con el vector de estimación de parámetros $X$ mediante un modelo lineal, y hay ruido $V$ en la observación que no está correlacionado con el parámetro estimado :

$Z = HX + V$, (1)

donde $H$ es la matriz de transformación que describe la relación entre los valores observados y los parámetros estimados.

La estimación $X$ que minimiza el error cuadrático se escribe de la siguiente manera:

$X_(ots)=(H^TR_V^(-1)H)^(-1)H^TR_V^(-1)Z$, (2)

Deje que el ruido $V$ no esté correlacionado, en cuyo caso la matriz $R_V$ es solo la matriz identidad, y la ecuación de estimación se vuelve más simple:

$X_(ots)=(H^TH)^(-1)H^TZ$, (3)

El registro en forma de matriz ahorra mucho papel, pero puede ser inusual para alguien. El siguiente ejemplo, tomado de la monografía de Yu.M. Korshunov "Fundamentos matemáticos de la cibernética", ilustra todo esto.
Se tiene el siguiente circuito eléctrico:

Los valores observados en este caso son las lecturas del instrumento $A_1 ​​= 1 A, A_2 = 2 A, V = 20 B$.

Además, se conoce la resistencia $R = 5$ Ohm. Se requiere estimar de la mejor manera, desde el punto de vista del criterio del error cuadrático medio mínimo, los valores de las corrientes $I_1$ y $I_2$. Lo más importante aquí es que exista alguna relación entre los valores observados (lecturas del instrumento) y los parámetros estimados. Y esta información es traída desde afuera.

En este caso, estas son las leyes de Kirchhoff, en el caso del filtrado (que se discutirá más adelante), un modelo de serie de tiempo autorregresivo, que supone que el valor actual depende de los anteriores.

Entonces, el conocimiento de las leyes de Kirchhoff, que de ninguna manera está relacionado con la teoría de las decisiones estadísticas, le permite establecer una conexión entre los valores observados y los parámetros estimados (los que estudiaron ingeniería eléctrica pueden verificar, el resto tendrá que confíe en su palabra):

$$z_1 = A_1 = I_1 + \xi_1 = 1$$

$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$

$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$

Esto es en forma de vector:

$$\begin(vmatriz) z_1\\ z_2\\ z_3 \end(vmatriz) = \begin(vmatriz) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatriz) \begin(vmatriz) I_1\ \ I_2 \end(vmatriz) + \begin(vmatriz) \xi_1\\ \xi_2\\ \xi_3 \end(vmatriz)$$

O $Z = HX + V$, donde

$$Z= \begin(vmatrix) z_1\\ z_2\\ z_3 \end(vmatrix) = \begin(vmatrix) 1\\ 2\\ 4 \end(vmatrix) ; H= \begin(vmatriz) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatriz) ; X= \begin(vmatrix) I_1\\ I_2 \end(vmatrix) ; V= \begin(vmatriz) \xi_1\\ \xi_2\\ \xi_3 \end(vmatriz)$$

Considerando los valores de ruido como no correlacionados entre sí, encontramos la estimación de I 1 e I 2 por el método de los mínimos cuadrados de acuerdo con la fórmula 3:

$H^TH= \begin(vmatriz) 1 & 1& 1\\ 0 & 1& 2 \end(vmatriz) \begin(vmatriz) 1 & 0\\ 1 & 1\\ 1 & 2 \end(vmatriz) = \ begin(vmatriz) 3 & 3\\ 3 & 5 \end(vmatriz) ; (H^TH)^(-1)= \frac(1)(6) \begin(vmatrix) 5 & -3\\ -3 & 3 \end(vmatrix) $;

$H^TZ= \begin(vmatriz) 1 & 1& 1\\ 0 & 1& 2 \end(vmatriz) \begin(vmatriz) 1 \\ 2\\ 4 \end(vmatriz) = \begin(vmatriz) 7\ \ 10 \end(vmatriz) ; X(vmatriz)= \frac(1)(6) \begin(vmatriz) 5 & -3\\ -3 & 3 \end(vmatriz) \begin(vmatriz) 7\\ 10 \end(vmatriz) = \frac (1)(6) \begin(vmatrix) 5\\ 9 \end(vmatrix)$;

Entonces $I_1 = 5/6 = 0.833 A$; $I_2 = 9/6 = 1,5 A$.

Tarea de filtrado

A diferencia de la tarea de estimar parámetros que tienen valores fijos, en el problema de filtración se requiere evaluar procesos, es decir, encontrar estimaciones actuales de una señal variable en el tiempo distorsionada por el ruido y, por tanto, inaccesible a la medición directa. En el caso general, el tipo de algoritmos de filtrado depende de las propiedades estadísticas de la señal y el ruido.

Supondremos que la señal útil es una función del tiempo que varía lentamente y que el ruido es un ruido no correlacionado. Usaremos el método de los mínimos cuadrados, nuevamente debido a la falta de información a priori sobre las características probabilísticas de la señal y el ruido.

Primero, obtenemos una estimación del valor actual de $x_n$ usando los últimos valores de $k$ de la serie de tiempo $z_n, z_(n-1),z_(n-2)\dots z_(n-( k-1))$. El modelo de observación es el mismo que en el problema de estimación de parámetros:

Está claro que $Z$ es un vector columna formado por los valores observados de la serie temporal $z_n, z_(n-1),z_(n-2)\dots z_(n-(k-1)) $, $V $ – vector de columna de ruido $\xi _n, \xi _(n-1),\xi_(n-2)\dots \xi_(n-(k-1))$, distorsionando la señal verdadera. ¿Y qué significan los símbolos $H$ y $X$? ¿De qué tipo de vector columna $X$, por ejemplo, podemos hablar si todo lo que se necesita es dar una estimación del valor actual de la serie de tiempo? Y lo que significa la matriz de transformación $H$ no está del todo claro.

Todas estas preguntas pueden responderse solo si se introduce en consideración el concepto de un modelo de generación de señales. Es decir, se necesita algún modelo de la señal original. Esto es comprensible, en ausencia de información a priori sobre las características probabilísticas de la señal y el ruido, solo queda hacer suposiciones. Puede llamarlo adivinación en el café molido, pero los expertos prefieren una terminología diferente. En su secador de pelo, esto se llama modelo paramétrico.

En este caso, se estiman los parámetros de este modelo en particular. Al elegir un modelo de generación de señal adecuado, recuerde que cualquier función analítica se puede expandir en una serie de Taylor. Una propiedad sorprendente de la serie de Taylor es que la forma de una función a cualquier distancia finita $t$ de algún punto $x=a$ está determinada únicamente por el comportamiento de la función en una vecindad infinitamente pequeña del punto $x=a $ (hablamos de sus derivadas de primer orden y de orden superior).

Así, la existencia de la serie de Taylor significa que la función analítica tiene una estructura interna con una conexión muy fuerte. Si, por ejemplo, nos restringimos a tres miembros de la serie de Taylor, entonces el modelo de generación de señales se verá así:

$x_(n-i) = F_(-i)x_n$, (4)

$$X_n= \begin(vmatriz) x_n\\ x"_n\\ x""_n \end(vmatriz) ; F_(-i)= \begin(vmatriz) 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end(vmatriz) $$

Es decir, la fórmula 4, con un orden dado del polinomio (en el ejemplo es igual a 2), establece una conexión entre el $n$-ésimo valor de la señal en la secuencia de tiempo y $(ni)$-ésimo . Así, el vector de estado estimado en este caso incluye, además del propio valor estimado, las derivadas primera y segunda de la señal.

En la teoría del control automático, dicho filtro se denominaría filtro astático de segundo orden. La matriz de transformación $H$ para este caso (la estimación se basa en las muestras actuales y $k-1$ anteriores) se ve así:

$$H= \begin(vmatrix) 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \ fin(vmatriz)$$

Todos estos números se obtienen de la serie de Taylor, suponiendo que el intervalo de tiempo entre los valores observados adyacentes es constante e igual a 1.

Así, el problema de filtrado, bajo nuestros supuestos, se ha reducido al problema de estimación de parámetros; en este caso, se estiman los parámetros del modelo de generación de señal adoptado por nosotros. Y la evaluación de los valores del vector de estado $X$ se realiza según la misma fórmula 3:

$$X_(ots)=(H^TH)^(-1)H^TZ$$

De hecho, hemos implementado un proceso de estimación paramétrica basado en un modelo autorregresivo del proceso de generación de señales.

La fórmula 3 se implementa fácilmente en el software, para esto es necesario completar la matriz $H$ y la columna del vector de observaciones $Z$. Estos filtros se llaman filtros de memoria finitos, ya que utilizan las últimas $k$ observaciones para obtener la estimación actual $X_(not)$. En cada nuevo paso de observación, se agrega un nuevo conjunto de observaciones al conjunto actual de observaciones y se descarta el antiguo. Este proceso de evaluación se denomina ventana deslizante.

Filtros de memoria creciente

Los filtros con memoria finita tienen la principal desventaja de que después de cada nueva observación, es necesario volver a calcular completamente todos los datos almacenados en la memoria. Además, el cálculo de las estimaciones solo puede iniciarse después de que se hayan acumulado los resultados de las primeras $k$ observaciones. Es decir, estos filtros tienen una larga duración del proceso transitorio.

Para hacer frente a esta deficiencia, es necesario pasar de un filtro con memoria permanente a un filtro con memoria creciente. En dicho filtro, el número de valores observados a evaluar debe coincidir con el número n de la observación actual. Esto permite obtener estimaciones a partir del número de observaciones igual al número de componentes del vector estimado $X$. Y esto está determinado por el orden del modelo adoptado, es decir, cuántos términos de la serie de Taylor se utilizan en el modelo.

Al mismo tiempo, a medida que aumenta n, mejoran las propiedades de suavizado del filtro, es decir, aumenta la precisión de las estimaciones. Sin embargo, la implementación directa de este enfoque está asociada con un aumento en los costos computacionales. Por lo tanto, los filtros de memoria creciente se implementan como recurrente.

El punto es que para el tiempo n ya tenemos la estimación $X_((n-1)ots)$, que contiene información sobre todas las observaciones anteriores $z_n, z_(n-1), z_(n-2) \dots z_ (n-(k-1))$. La estimación $X_(not)$ se obtiene mediante la siguiente observación $z_n$ utilizando la información almacenada en la estimación $X_((n-1))(\mbox (ot))$. Este procedimiento se denomina filtrado recurrente y consiste en lo siguiente:

• según la estimación $X_((n-1))(\mbox (ots))$, la estimación $X_n$ se predice mediante la fórmula 4 para $i = 1$: $X_(\mbox (noca priori)) = F_1X_((n-1)ots)$. Esta es una estimación a priori;
• de acuerdo con los resultados de la observación actual $z_n$, esta estimación a priori se convierte en una verdadera, es decir, a posteriori;
• este procedimiento se repite en cada paso, comenzando desde $r+1$, donde $r$ es el orden de filtrado.

La fórmula final de filtrado recursivo se ve así:

$X_((n-1)ots) = X_(\mbox (nocapriori)) + (H^T_nH_n)^(-1)h^T_0(z_n - h_0 X_(\mbox (nocapriori)))$, (6 )

donde para nuestro filtro de segundo orden:

El filtro de memoria creciente que funciona según la fórmula 6 es un caso especial del algoritmo de filtrado conocido como filtro de Kalman.

En la implementación práctica de esta fórmula, hay que recordar que la estimación a priori incluida en ella viene determinada por la fórmula 4, y el valor $h_0 X_(\mbox (nocapriori))$ es la primera componente del vector $X_( \mbox (nocapriori))$.

El filtro de memoria creciente tiene una característica importante. Mirando la Fórmula 6, el puntaje final es la suma del vector de puntaje previsto y el término de corrección. Esta corrección es grande para $n$ pequeños y disminuye a medida que aumenta $n$, tendiendo a cero cuando $n \rightarrow \infty$. Es decir, a medida que n crece, las propiedades de suavizado del filtro crecen y el modelo incrustado en él comienza a dominar. Pero la señal real puede corresponder al modelo solo en algunas áreas, por lo que la precisión del pronóstico se deteriora.

Para combatir esto, a partir de unos $n$, se impone la prohibición de seguir reduciendo el plazo de corrección. Esto es equivalente a cambiar la banda del filtro, es decir, para n pequeño, el filtro es más ancho (menos inercial), para n grande, se vuelve más inercial.

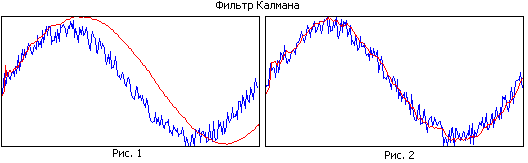
Compare la Figura 1 y la Figura 2. En la primera figura, el filtro tiene una gran memoria, mientras que suaviza bien, pero debido a la banda estrecha, la trayectoria estimada va a la zaga de la real. En la segunda figura, la memoria del filtro es más pequeña, suaviza peor, pero sigue mejor la trayectoria real.

Literatura

1. Yu.M.Korshunov "Fundamentos matemáticos de la cibernética"
2. A.V.Balakrishnan "Teoría de la filtración de Kalman"
3. VN Fomin "Estimación recurrente y filtrado adaptativo"
4. CFN Cowen, PM Otorgar "Filtros adaptables"

Este filtro se utiliza en varios campos, desde la ingeniería de radio hasta la economía. Aquí discutiremos la idea principal, el significado, la esencia de este filtro. Se presentará en el lenguaje más simple posible.
Supongamos que tenemos la necesidad de medir algunas cantidades de algún objeto. En ingeniería de radio, la mayoría de las veces se ocupan de medir voltajes en la salida de un determinado dispositivo (sensor, antena, etc.). En el ejemplo con un electrocardiógrafo (ver), estamos tratando con mediciones de biopotenciales en el cuerpo humano. En economía, por ejemplo, el valor medido puede ser el tipo de cambio. Todos los días el tipo de cambio es diferente, i.е. cada día "sus medidas" nos dan un valor diferente. Y para generalizar, podemos decir que la mayor parte de la actividad humana (si no toda) se reduce a mediciones-comparaciones constantes de ciertas cantidades (ver el libro).
Así que digamos que medimos algo todo el tiempo. Supongamos también que nuestras medidas siempre vienen con algún error; esto es comprensible, porque no hay instrumentos de medida ideales, y todo el mundo da un resultado con un error. En el caso más simple, esto se puede reducir a la siguiente expresión: z=x+y, donde x es el verdadero valor que queremos medir y mediríamos si tuviéramos un dispositivo de medición ideal, y es el error de medición introducido por el dispositivo de medición, y z es el valor que medimos. Entonces, la tarea del filtro de Kalman es seguir adivinando (determinar) a partir de la z que medimos, y cuál era el verdadero valor de x cuando recibimos nuestra z (en la que el valor verdadero y el error de medición "se sientan"). Es necesario filtrar (descartar) el verdadero valor de x de z - eliminar el ruido distorsionador y de z. Es decir, teniendo solo la cantidad disponible, necesitamos adivinar qué términos dieron esta cantidad.
A la luz de lo anterior, ahora formulamos todo de la siguiente manera. Que sólo haya dos números aleatorios. Sólo se nos da su suma y estamos obligados a determinar a partir de esta suma cuáles son los términos. Por ejemplo, nos dieron el número 12 y dicen: 12 es la suma de los números x e y, la pregunta es a qué son iguales x e y. Para responder a esta pregunta, hacemos la ecuación: x+y=12. Obtuvimos una ecuación con dos incógnitas, por lo tanto, estrictamente hablando, no es posible encontrar dos números que den esta suma. Pero todavía podemos decir algo sobre estos números. Podemos decir que eran los números 1 y 11, o 2 y 10, o 3 y 9, o 4 y 8, etc., también son 13 y -1, o 14 y -2, o 15 y - 3 etc Es decir, mediante la suma (en nuestro ejemplo 12) podemos determinar el conjunto de opciones posibles que dan exactamente 12 en total. Una de estas opciones es el par que estamos buscando, que en realidad dio 12 en este momento. También vale la pena observando que todas las variantes de pares de números que dan en la suma 12 forman una línea recta que se muestra en la Fig. 1, que viene dada por la ecuación x+y=12 (y=-x+12).

Figura 1

Por lo tanto, el par que estamos buscando se encuentra en algún lugar de esta línea recta. Repito, es imposible elegir entre todas estas opciones el par que realmente existió, que dio el número 12, sin tener pistas adicionales. Pero, en la situación para la que se inventó el filtro de Kalman, hay tales sugerencias. Hay algo que se sabe de antemano acerca de los números aleatorios. En particular, allí se conoce el llamado histograma de distribución para cada par de números. Por lo general, se obtiene después de observaciones suficientemente prolongadas de las consecuencias de estos números muy aleatorios. Es decir, por ejemplo, se sabe por experiencia que en el 5% de los casos el par x=1, y=8 generalmente se cae (denotamos este par de la siguiente manera: (1,8)), en el 2% de los casos el par par x=2, y=3 (2,3), en el 1% de los casos una pareja (3,1), en el 0,024% de los casos una pareja (11,1), etc. Nuevamente, este histograma se establece para todas las parejas números, incluidos los que suman 12. Así, por cada par que sume 12, podemos decir que, por ejemplo, el par (1, 11) cae en el 0,8% de los casos, el par ( 2, 10) - en el 1% de los casos, par (3, 9) - en el 1,5% de los casos, etc. Así, podemos determinar a partir del histograma en qué porcentaje de casos la suma de los términos de un par es 12. Sea, por ejemplo, en el 30% de los casos la suma da 12. Y en el 70% restante, los pares restantes caen fuera - estos son (1.8), (2, 3), (3,1), etc. - los que suman números distintos de 12. Además, supongamos que, por ejemplo, un par (7,5) cae en el 27% de los casos, mientras que todos los demás pares que dan un total de 12 caen en 0,024% + 0,8% + 1%+1,5%+…=3% de los casos. Entonces, de acuerdo con el histograma, descubrimos que los números que dan un total de 12 caen en el 30% de los casos. Al mismo tiempo, sabemos que si cayeron 12, entonces la mayoría de las veces (27% de 30%) la razón de esto es un par (7.5). es decir, si ya 12 tirados, podemos decir que en el 90% (27% del 30% -o lo que es lo mismo, 27 veces de cada 30) el motivo de la tirada de 12 es un par (7,5). Sabiendo que el par (7,5) suele ser la razón por la que la suma es igual a 12, es lógico suponer que, muy probablemente, se cayó ahora. Por supuesto, todavía no es un hecho que el número 12 esté realmente formado por este par en particular, sin embargo, la próxima vez, si nos encontramos con 12, y nuevamente asumimos un par (7.5), entonces en algún lugar en el 90% de los casos estamos 100% correcto. Pero si asumimos un par (2, 10), acertaremos solo el 1% del 30% de las veces, lo que equivale a un 3,33% de aciertos frente al 90% al acertar un par (7,5). Eso es todo: este es el objetivo del algoritmo de filtro de Kalman. Es decir, el filtro de Kalman no garantiza que no se equivoque al determinar el sumando, pero sí que se equivocará el mínimo número de veces (la probabilidad de error será mínima), ya que utiliza estadísticas - un histograma de caída de pares de números. También se debe enfatizar que la llamada densidad de distribución de probabilidad (PDD) se usa a menudo en el algoritmo de filtrado de Kalman. Sin embargo, debe entenderse que el significado allí es el mismo que el del histograma. Además, un histograma es una función construida sobre la base de PDF y siendo su aproximación (ver, por ejemplo, ).
En principio, podemos representar este histograma como una función de dos variables, es decir, como una especie de superficie sobre el plano xy. Donde la superficie es más alta, la probabilidad de que se caiga el par correspondiente también es mayor. La figura 2 muestra una superficie de este tipo.

Figura 2

Como puede ver, arriba de la línea x + y = 12 (que son variantes de pares que dan un total de 12), hay puntos de superficie a diferentes alturas y la altura más alta está en la variante con coordenadas (7,5). Y cuando nos encontramos con una suma igual a 12, en el 90% de los casos el par (7,5) es el motivo de la aparición de esta suma. Aquellos. es este par, que suma 12, el que tiene mayor probabilidad de ocurrir, siempre que la suma sea 12.
Por lo tanto, aquí se describe la idea detrás del filtro de Kalman. Es en él que se construyen todo tipo de modificaciones: de un solo paso, recurrentes de varios pasos, etc. Para un estudio más profundo del filtro de Kalman, recomiendo el libro: Van Tries G. Teoría de detección, estimación y modulación.

PD. Para aquellos que estén interesados ​​en explicar los conceptos de las matemáticas, lo que se llama "en los dedos", podemos recomendar este libro y, en particular, los capítulos de su sección "Matemáticas" (puede adquirir el libro o los capítulos individuales en eso).

Random Forest es uno de mis algoritmos de minería de datos favoritos. En primer lugar, es increíblemente versátil, se puede utilizar para resolver problemas de regresión y clasificación. Busque anomalías y seleccione predictores. En segundo lugar, este es un algoritmo que es realmente difícil de aplicar incorrectamente. Simplemente porque, a diferencia de otros algoritmos, tiene pocos parámetros personalizables. Y, sin embargo, es sorprendentemente simple en su esencia. Al mismo tiempo, es notablemente preciso.

¿Cuál es la idea de un algoritmo tan maravilloso? La idea es simple: digamos que tenemos un algoritmo muy débil, digamos . Si hacemos muchos modelos diferentes usando este algoritmo débil y promediamos el resultado de sus predicciones, entonces el resultado final será mucho mejor. Este es el llamado aprendizaje conjunto en acción. Por lo tanto, el algoritmo Random Forest se llama "Random Forest", por los datos recibidos, crea muchos árboles de decisión y luego promedia el resultado de sus predicciones. Un punto importante aquí es el elemento de aleatoriedad en la creación de cada árbol. Después de todo, está claro que si creamos muchos árboles idénticos, el resultado de su promedio tendrá la precisión de un árbol.

¿Cómo trabaja? Supongamos que tenemos algunos datos de entrada. Cada columna corresponde a algún parámetro, cada fila corresponde a algún elemento de datos.

Podemos elegir, al azar, varias columnas y filas de todo el conjunto de datos y construir un árbol de decisión a partir de ellas.

jueves, 10 de mayo de 2012

jueves, 12 de enero de 2012

Eso es todo. El vuelo de 17 horas ha terminado, Rusia se ha quedado en el extranjero. Y a través de la ventana de un acogedor apartamento de 2 habitaciones, San Francisco, el famoso Silicon Valley, California, EE.UU. nos mira. Sí, esta es precisamente la razón por la que no he escrito mucho últimamente. Nos mudamos.

Todo comenzó en abril de 2011 cuando tuve una entrevista telefónica con Zynga. Entonces todo parecía una especie de juego que no tenía nada que ver con la realidad, y no podía ni imaginar a qué me conduciría. En junio de 2011, Zynga vino a Moscú y realizó una serie de entrevistas, se consideraron alrededor de 60 candidatos que aprobaron una entrevista telefónica y se seleccionaron alrededor de 15 personas (no sé el número exacto, alguien más tarde cambió de opinión, alguien se negó inmediatamente). La entrevista resultó ser sorprendentemente simple. Sin tareas de programación para usted, sin preguntas intrincadas sobre la forma de las escotillas, principalmente se probó la capacidad de chatear. Y el conocimiento, en mi opinión, se evaluó solo superficialmente.

Y entonces comenzó el galimatías. Primero esperamos los resultados, luego la oferta, luego la aprobación de la LCA, luego la aprobación de la solicitud de visa, luego los documentos de los EE. UU., luego la fila en la embajada, luego el cheque adicional, luego la visa. A veces me parecía que estaba dispuesto a dejarlo todo y anotar. Por momentos dudé si necesitamos a esta América, porque Rusia tampoco es mala. Todo el proceso tomó alrededor de medio año, al final, a mediados de diciembre, recibimos las visas y comenzamos a prepararnos para la salida.

El lunes fue mi primer día en el nuevo trabajo. La oficina tiene todas las condiciones no solo para trabajar, sino también para vivir. Desayunos, comidas y cenas de la mano de nuestros propios chefs, un montón de comida variada repleta por todos los rincones, gimnasio, masajes y hasta peluquería. Todo esto es completamente gratis para los empleados. Muchos llegan al trabajo en bicicleta y varias salas están habilitadas para guardar vehículos. En general, nunca he visto algo así en Rusia. Sin embargo, todo tiene su precio, inmediatamente nos advirtieron que tendríamos que trabajar mucho. Lo que es "mucho", según sus estándares, no me queda muy claro.

Sin embargo, espero que, a pesar de la cantidad de trabajo, en un futuro previsible pueda volver a escribir blogs y tal vez contar algo sobre la vida estadounidense y el trabajo como programador en Estados Unidos. Espera y verás. Mientras tanto, les deseo a todos una Feliz Navidad y un Próspero Año Nuevo y ¡hasta pronto!

Como ejemplo de uso, imprimamos la rentabilidad por dividendo de las empresas rusas. Como precio base, tomamos el precio de cierre de la acción el día que se cierra el registro. Por alguna razón, esta información no está disponible en el sitio web de Troika y es mucho más interesante que los valores absolutos de los dividendos.
¡Atención! El código tarda mucho tiempo en ejecutarse, porque para cada acción, debe realizar una solicitud a los servidores financieros y obtener su valor.

resultado<- NULL for(i in (1:length(divs[,1]))){ d <- divs if (d$Divs>0)( prueba(( comillas<- getSymbols(d$Symbol, src="Finam", from="2010-01-01", auto.assign=FALSE) if (!is.nan(quotes)){ price <- Cl(quotes) if (length(price)>0)(dd<- d$Divs result <- rbind(result, data.frame(d$Symbol, d$Name, d$RegistryDate, as.numeric(dd)/as.numeric(price), stringsAsFactors=FALSE)) } } }, silent=TRUE) } } colnames(result) <- c("Symbol", "Name", "RegistryDate", "Divs") result

Del mismo modo, puede crear estadísticas de años anteriores.

Dio la casualidad de que realmente me gustan todo tipo de algoritmos que tienen una justificación matemática clara y lógica) Pero a menudo su descripción en Internet está tan sobrecargada de fórmulas y cálculos que es simplemente imposible entender el significado general del algoritmo. Pero comprender la esencia y el principio del dispositivo/mecanismo/algoritmo es mucho más importante que memorizar fórmulas enormes. No importa lo trillado que parezca, pero recordar incluso cientos de fórmulas no ayudará si no sabes cómo y dónde aplicarlas 😉 En realidad, ¿para qué es todo esto? Decidí revolver la descripción de algunos algoritmos que Tuve que lidiar con en la práctica. Intentaré no sobrecargarme con cálculos matemáticos para que el material sea comprensible y fácil de leer.

Y hoy hablaremos de filtro Kalman Averigüemos qué es, por qué y cómo se usa.

Comencemos con un pequeño ejemplo. Supongamos que nos enfrentamos a la tarea de determinar las coordenadas de un avión en vuelo. Y, por supuesto, la coordenada (la denotamos) debe determinarse con la mayor precisión posible.

En el avión preinstalamos un sensor que nos da los datos de ubicación que buscamos, pero como todo en este mundo, nuestro sensor no es perfecto. Entonces, en lugar de un valor, obtenemos:

donde es el error del sensor, es decir, una variable aleatoria. Así, a partir de las lecturas inexactas de los equipos de medición, debemos obtener el valor de la coordenada (), lo más cercana posible a la posición real de la aeronave.

La tarea está establecida, pasemos a su solución.

Háganos saber la acción de control () debido a la cual vuela el avión (el piloto nos dijo qué palancas tira 😉). Entonces, conociendo la coordenada en el paso k-ésimo, podemos obtener el valor en el paso (k+1):

¡Parecería, aquí está, lo que necesitas! Y aquí no se necesita ningún filtro de Kalman. Pero no todo es tan sencillo. En realidad, no podemos tener en cuenta todos los factores externos que afectan al vuelo, por lo que la fórmula toma la siguiente forma:

donde es un error causado por influencia externa, imperfección del motor, etc.

¿Así que lo que ocurre? En el paso (k+1) tenemos, en primer lugar, una lectura del sensor imprecisa y, en segundo lugar, un valor calculado incorrectamente, obtenido a partir del valor del paso anterior.

La idea del filtro de Kalman es obtener una estimación exacta de la coordenada requerida (para nuestro caso) a partir de dos valores inexactos (tomándolos con diferentes coeficientes de peso). En el caso general, el valor medido puede ser absolutamente cualquiera (temperatura, velocidad...). Esto es lo que sucede:

A través de cálculos matemáticos, podemos obtener una fórmula para calcular el coeficiente de Kalman en cada paso, pero, como se acordó al comienzo del artículo, no profundizaremos en los cálculos, sobre todo porque se ha establecido en la práctica que el coeficiente de Kalman siempre tiende a un cierto valor con el aumento de k. Obtenemos la primera simplificación de nuestra fórmula:

Supongamos ahora que no hay comunicación con el piloto, y no conocemos la acción de control. Parecería que en este caso no podemos usar el filtro de Kalman, pero esto no es así 😉 Simplemente "desechamos" lo que no sabemos de la fórmula, luego

Obtenemos la fórmula de Kalman más simplificada, que, sin embargo, a pesar de tales simplificaciones "difíciles", hace frente a su tarea perfectamente. Si representas los resultados gráficamente, obtienes algo como esto:

Si nuestro sensor es muy preciso, entonces, naturalmente, el factor de ponderación K debería estar cerca de la unidad. Si la situación es a la inversa, es decir, nuestro sensor no es muy bueno, entonces K debería estar más cerca de cero.

Esto, quizás, es todo, solo así, ¡acabamos de descubrir el algoritmo de filtrado de Kalman! Espero que el artículo haya sido útil y comprensible =)